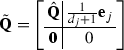Abstract
SimRank is an appealing pair-wise similarity measure based on graph structure. It iteratively follows the intuition that two nodes are assessed as similar if they are pointed to by similar nodes. Many real graphs are large, and links are constantly subject to minor changes. In this article, we study the efficient dynamical computation of all-pairs SimRanks on time-varying graphs. Existing methods for the dynamical SimRank computation [e.g., LTSF (Shao et al. in PVLDB 8(8):838–849, 2015) and READS (Zhang et al. in PVLDB 10(5):601–612, 2017)] mainly focus on top-k search with respect to a given query. For all-pairs dynamical SimRank search, Li et al.’s approach (Li et al. in EDBT, 2010) was proposed for this problem. It first factorizes the graph via a singular value decomposition (SVD) and then incrementally maintains such a factorization in response to link updates at the expense of exactness. As a result, all pairs of SimRanks are updated approximately, yielding \(O({r}^{4}n^2)\) time and \(O({r}^{2}n^2)\) memory in a graph with n nodes, where r is the target rank of the low-rank SVD. Our solution to the dynamical computation of SimRank comprises of five ingredients: (1) We first consider edge update that does not accompany new node insertions. We show that the SimRank update \({\varvec{\Delta }}{} \mathbf{S}\) in response to every link update is expressible as a rank-one Sylvester matrix equation. This provides an incremental method requiring \(O(Kn^2)\) time and \(O(n^2)\) memory in the worst case to update \(n^2\) pairs of similarities for K iterations. (2) To speed up the computation further, we propose a lossless pruning strategy that captures the “affected areas” of \({\varvec{\Delta }}{} \mathbf{S}\) to eliminate unnecessary retrieval. This reduces the time of the incremental SimRank to \(O(K(m+|{\textsf {AFF}}|))\), where m is the number of edges in the old graph, and \(|{\textsf {AFF}}| \ (\le n^2)\) is the size of “affected areas” in \({\varvec{\Delta }}{} \mathbf{S}\), and in practice, \(|{\textsf {AFF}}| \ll n^2\). (3) We also consider edge updates that accompany node insertions, and categorize them into three cases, according to which end of the inserted edge is a new node. For each case, we devise an efficient incremental algorithm that can support new node insertions and accurately update the affected SimRanks. (4) We next study batch updates for dynamical SimRank computation, and design an efficient batch incremental method that handles “similar sink edges” simultaneously and eliminates redundant edge updates. (5) To achieve linear memory, we devise a memory-efficient strategy that dynamically updates all pairs of SimRanks column by column in just \(O(Kn+m)\) memory, without the need to store all \((n^2)\) pairs of old SimRank scores. Experimental studies on various datasets demonstrate that our solution substantially outperforms the existing incremental SimRank methods and is faster and more memory-efficient than its competitors on million-scale graphs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recent rapid advances in Web data management reveal that link analysis is becoming an important tool for similarity assessment. Due to the growing number of applications in e.g., social networks, recommender systems, citation analysis, and link prediction [9], a surge of graph-based similarity measures have surfaced over the past decade. For instance, Brin and Page [2] proposed a very successful relevance measure, called Google PageRank, to rank Web pages. Jeh and Widom [9] devised SimRank, an appealing pair-wise similarity measure that quantifies the structural equivalence of two nodes based on link structure. Recently, Sun et al. [21] invented PathSim to retrieve nodes proximities in a heterogeneous graph. Among these emerging link based measures, SimRank has stood out as an attractive one in recent years, due to its simple and iterative philosophy that “two nodes are similar if they are pointed to by similar nodes,” coupled with the base case that “every node is most similar to itself.” This recursion not only allows SimRank to capture the global structure of a graph, but also equips SimRank with mathematical insights that attract many researchers. For example, Fogaras and Rácz [5] interpreted SimRank as the meeting time of the coalescing pair-wise random walks. Li et al. [13] harnessed an elegant matrix equation to formulate the closed form of SimRank.
Nevertheless, the batch computation of SimRank is costly: \(O(Kd'n^2)\) time for all node pairs [24], where K is the total number of iterations, and \(d' \le d\) (d is the average in-degree of a graph). Generally, many real graphs are large, with links constantly evolving with minor changes. This is especially apparent in e.g., co-citation networks, Web graphs, and social networks. As a statistical example [17, 31], there are 5–10% links updated every week in a Web graph. It is rather expensive to recompute similarities for all pairs of nodes from scratch when a graph is updated. Fortunately, we observe that when link updates are small, the affected areas for SimRank updates are often small as well. With this comes the need for incremental algorithms that compute changes to SimRank in response to link updates, to discard unnecessary recomputations. In this article, we investigate the following problem for SimRank evaluation:
- Problem :
-
(Incremental SimRank Computation)
- Given :
-
an old digraph G, old similarities in G, link changes \(\Delta G\) Footnote 1 to G, and a damping factor \(C \in (0,1)\).
- Retrieve :
-
the changes to the old similarities.
Our research for the above SimRank problem is motivated by the following real application:
Example 1
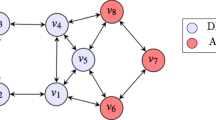
(Decentralize large-scale SimRank retrieval) Consider the Web graph G in Fig. 1. There are \(n=14\) nodes (web pages) in G, and each edge is a hyperlink. To evaluate the SimRank scores of all \(({n} \times n)\) pairs of Web pages in G, existing all-pairs SimRank algorithms need iteratively compute the SimRank matrix \(\mathbf {S}\) of size \(({n} \times n)\) in a centralized way (by using a single machine). In contrast, our incremental approach can significantly improve the computational efficiency of all pairs of SimRanks by retrieving \(\mathbf {S}\) in a decentralized way as follows:
We first employ a graph partitioning algorithm (e.g., METISFootnote 2) that can decompose the large graph G into several small blocks such that the number of the edges with endpoints in different blocks is minimized. In this example, we partition G into 3 blocks, \(G_1 \cup G_2 \cup G_3\), along with 2 edges \(\{(f,c),(f,k)\}\) across the blocks, as depicted in the first row of Fig. 1.
Let \(G_{{\mathrm{old}}}:= G_1 \cup G_2 \cup G_3\) and \(\Delta G:=\{(f,c),(f,k)\}\). Then, G can be viewed as “\(G_{{\mathrm{old}}}\) perturbed by \(\Delta G\) edge insertions.” That is,
Based on this decomposition, we can efficiently compute \(\mathbf {S}\) over G by dividing \(\mathbf {S}\) into two parts:
where \(\mathbf {S}_{{\mathrm{old}}}\) is obtained by using a batch SimRank algorithm over \(G_{{\mathrm{old}}}\), and \({\varvec{\Delta }}{} \mathbf{S}\) is derived from our proposed incremental method which takes \(\mathbf {S}_{{\mathrm{old}}}\) and \(\Delta G\) as input.
It is worth mentioning that this way of retrieving \(\mathbf {S}\) is far more efficient than directly computing \(\mathbf {S}\) over G via a batch algorithm. There are two reasons:
Firstly, \(\mathbf {S}_{{\mathrm{old}}}\) can be efficiently computed in a decentralized way. It is a block diagonal matrix with no need of \(n \times n\) space to store \(\mathbf {S}_{{\mathrm{old}}}\). This is because \(G_{{\mathrm{old}}}\) is only comprised of several connected components \((G_1, G_2, G_3)\), and there are no edges across distinct components. Thus, \(\mathbf {S}_{{\mathrm{old}}}\) exhibits a block diagonal structure:

To obtain \(\mathbf {S}_{{\mathrm{old}}}\), instead of applying the batch SimRank algorithm over the entire \(G_{{\mathrm{old}}}\), we can apply the batch SimRank algorithm over each component \(G_i \ (i=1,2,3)\) independently to obtain the ith diagonal block of \(\mathbf {S}_{{\mathrm{old}}}\), \(\mathbf {S}_{G_i}\). Indeed, each \(\mathbf {S}_{G_i}\) is computable in parallel. Even if \(\mathbf {S}_{{\mathrm{old}}}\) is computed using a single machine, only \(O(n_1^2+n_2^2+n_3^2)\) space is required to store its diagonal blocks, where \(n_i\) is the number of nodes in each \(G_i\), rather than \(O(n^2)\) space to store the entire \(\mathbf {S}_{{\mathrm{old}}}\) (see Fig. 1).
Secondly, after graph partitioning, there are not many edges across components. Small size of \(\Delta G\) often leads to sparseness of \({\varvec{\Delta }}{} \mathbf{S}\) in general. Hence, \({\varvec{\Delta }}{} \mathbf{S}\) is stored in a sparse format. In addition, our incremental SimRank method will greatly accelerate the computation of \({\varvec{\Delta }}{} \mathbf{S}\).
Hence, along with graph partitioning, our incremental SimRank research will significantly enhance the computational efficiency of SimRank on large graphs, using a decentralized fashion. \(\square \)
Despite its usefulness, existing work on incremental SimRank computation is rather limited. To the best of our knowledge, there is a relative paucity of work [10, 13, 20, 25] on incremental SimRank problems. Shao et al. [20] proposed a novel two-stage random-walk sampling scheme, named TSF, which can support top-k SimRank search over dynamic graphs. In the preprocessing stage, TSF samples \(R_g\) one-way graphs that serve as an index for querying process. At query stage, for each one-way graph, \(R_q\) new random walks of node u are sampled. However, the dynamic SimRank problems studied in [20] and this work are different: This work focuses on all \((n^2)\) pairs of SimRank retrieval, which requires \(O(K(m+|{\textsf {AFF}}|))\) time to compute the entire matrix \(\mathbf {S}\) in a deterministic style. In Sect. 7, we have proposed a memory-efficient version of our incremental method that updates all pairs of similarities in a column-by-column fashion within only \(O(Kn+m)\) memory. In comparison, Shao et al. [20] focuses on top-k SimRank dynamic search w.r.t. a given query u. It incrementally retrieves only \(k \ (\le n)\) nodes with highest SimRank scores in a single column \(\mathbf {S}_{\star ,u}\), which requires \(O(K^2 R_q R_g)\) average query timeFootnote 3 to retrieve \(\mathbf {S}_{\star ,u}\) along with \(O(n \log k)\) time to return top-k results from \(\mathbf {S}_{\star ,u}\). Recently, Jiang et al. [10] pointed out that the probabilistic error guarantee of Shao et al.’s method is based on the assumption that no cycle in the given graph has a length shorter than K, and they proposed READS, a new efficient indexing scheme that improves precision and indexing space for dynamic SimRank search. The querying time of READS is O(rn) to retrieve one column \(\mathbf {S}_{\star ,u}\), where r is the number of sets of random walks. Hence, TSF and READS are highly efficient for top- k single-source SimRank search. Moreover, optimization methods in this work are based on a rank-one Sylvester matrix equation characterizing changes to the entire SimRank matrix \(\mathbf {S}\) for all-pairs dynamical search, which is fundamentally different from [10, 20]’s methods that maintain one-way graphs (or SA forests) updating. It is important to note that, for large-scale graphs, our incremental methods do not need to memorize all \((n^2)\) pairs of old SimRank scores. Instead, \(\mathbf {S}\) can be dynamically updated column-wisely in \(O(Kn+m)\) memory. For updating each column of \(\mathbf {S}\), our experiments in Sect. 8 verify that our memory-efficient incremental method is scalable on large real graphs while running 4–7x faster than the dynamical TSF [20] per edge update, due to the high cost of [20] merging one-way graph’s log buffers for TSF indexing.
Among the existing studies [10, 13, 20] on dynamical SimRank retrieval, the problem setting of Li et al.’s [13] on all-pairs dynamic search is exactly the same as ours: the goal is to retrieve changes \({\varvec{\Delta }}{} \mathbf{S}\) to all-pairs SimRank scores \(\mathbf {S}\), given old graph G, link changes \(\Delta G\) to G. To address this problem, the central idea of [13] is to factorize the backward transition matrix \(\mathbf {Q}\) of the original graph into \(\mathbf {U} \cdot {\varvec{\Sigma }} \cdot {\mathbf {V}}^\mathrm{T}\) via a singular value decomposition (SVD) first, and then incrementally estimate the updated matrices of \(\mathbf {U}\), \({\varvec{\Sigma }}\), \({\mathbf {V}}^\mathrm{T}\) for link changes at the expense of exactness. Consequently, updating all pairs of similarities entails \(O({r}^{4}n^2)\) time and \(O({r}^{2}n^2)\) memory yet without guaranteed accuracy, where \(r \ (\le n)\) is the target rank of the low-rank SVD approximation.Footnote 4 This method is efficient to graphs when r is extremely small, e.g., a star graph \((r=1)\). However, in general, r is not always negligibly small.
(Please refer to “Appendix A” [32] for a discussion in detail, and “Appendix C” [32] for an example.)
1.1 Main contributions
Motivated by this, we propose an efficient and accurate scheme for incrementally computing all-pairs SimRanks on link-evolving graphs. Our main contributions consist of the following five ingredients:
-
We first focus on unit edge update that does not accompany new node insertions. By characterizing the SimRank update matrix \({\varvec{\Delta }}{} \mathbf{S}\) w.r.t. every link update as a rank-one Sylvester matrix equation, we devise a fast incremental SimRank algorithm, which entails \(O(Kn^2)\) time in the worst case to update \(n^2\) pairs of similarities for K iterations (Sect. 3).
-
To speed up the computation further, we also propose an effective pruning strategy that captures the “affected areas” of \({\varvec{\Delta }}{} \mathbf{S}\) to discard unnecessary retrieval (e.g., the grey cells in Fig. 2), without loss of accuracy. This reduces the time of incremental SimRank to \(O(K(m+|{\textsf {AFF}}|))\), where \(|{\textsf {AFF}}| \ (\le n^2)\) is the size of “affected areas” in \({\varvec{\Delta }}{} \mathbf{S}\), and in practice, \(|{\textsf {AFF}}| \ll n^2\) (Sect. 4).
-
We also consider edge updates that accompany new node insertions, and distinguish them into three categories, according to which end of the inserted edge is a new node. For each case, we devise an efficient incremental SimRank algorithm that can support new nodes insertion and accurately update affected SimRank scores (Sect. 5).
-
We next investigate the batch updates of dynamical SimRank computation. Instead of dealing with each edge update one by one, we devise an efficient algorithm that can handle a sequence of edge insertions and deletions simultaneously, by merging “similar sink edges” and minimizing unnecessary updates (Sect. 6).
-
To achieve linear memory efficiency, we also express \({\varvec{\Delta }}{} \mathbf{S}\) as the sum of many rank-one tensor products, and devise a memory-efficient technique that updates all-pairs SimRanks in a column-by-column style in \(O(Kn+m)\) memory, without loss of exactness. (Sect. 7)
-
We conduct extensive experiments on real and synthetic datasets to demonstrate that our algorithm (a) is consistently faster than the existing incremental methods from several times to over one order of magnitude; (b) is faster than its batch counterparts especially when link updates are small; (c) for batch updates, runs faster than the repeated unit update algorithms; (d) entails linear memory and scales well on billion-edge graphs for all-pairs SimRank update; (e) is faster than LTSF and its memory space is less than LTSF; (f) entails more time on Cases (C0) and (C2) than Cases (C1) and (C3) for four edge types, and Case (C3) runs the fastest (Sect. 8).
This article is a substantial extension of our previous work [25]. We have made the following new updates: (1) In Sect. 5, we study three types of edge updates that accompany new node insertions. This solidly extends [25] and Li et al.’s incremental method [13] whose edge updates disallow node changes. (2) In Sect. 6, we also investigate batch updates for dynamic SimRank computation, and devise an efficient algorithm that can handle “similar sink edges” simultaneously and discard unnecessary unit updates further. (3) In Sect. 7, we propose a memory-efficient strategy that significantly reduces the memory from \(O(n^2)\) to \(O(Kn+m)\) for incrementally updating all pairs of SimRanks on million-scale graphs, without compromising running time and accuracy. (4) In Sect. 8, we conduct additional experiments on real and synthetic datasets to verify the high scalability and fast computational time of our memory-efficient methods, as compared with the LTSF method. (5) In Sect. 9, we update the related work section by incorporating state-of-the-art SimRank research.
2 SimRank background
In this section, we give a broad overview of SimRank. Intuitively, the central theme behind SimRank is that “two nodes are considered as similar if their incoming neighbors are themselves similar.” Based on this idea, there have emerged two widely used SimRank models: (1) Li et al.’s model (e.g., [6, 8, 13, 18, 26, 28, 30]) and (2) Jeh and Widom’s model (e.g., [4, 9, 11, 16, 20, 29]). Throughout this article, our focus is on Li et al.’s SimRank model, also known as Co-SimRank in [18], since the recent work [18] by Rothe and Schütze has showed that Co-SimRank is more accurate than Jeh and Widom’s SimRank model in real applications such as bilingual lexicon extraction. (Please refer to Remark 1 for detailed explanations.)
2.1 Li et al.’s SimRank model
Given a directed graph \({G}=({V},{E})\) with a node set V and an edge set E, let \(\mathbf {Q}\) be its backward transition matrix (that is, the transpose of the column-normalized adjacency matrix), whose entry \([\mathbf {Q}]_{i,j}=1/\text {in-degree}(i)\) if there is an edge from j to i, and 0 otherwise. Then, Li et al.’s SimRank matrix, denoted by \(\mathbf {S}\), is defined as
where \(C \in \left( 0,1 \right) \) is a damping factor, which is generally taken to be 0.6–0.8, and \(\mathbf {I}_n\) is an \(n \times n\) identity matrix \((n=|V|)\). The notation \({(\star )}^\mathrm{T}\) is the matrix transpose.
Recently, Rothe and Schütze [18] have introduced Co-SimRank, whose definition is
Comparing Eqs. (1) and (2), we can readily verify that Li et al.’s SimRank scores equal Co-SimRank scores scaled by a constant factor \((1-C)\), i.e., \({{\mathbf {S}}} = (1-C) \cdot {{{\tilde{\mathbf{S}}}}}\). Hence, the relative order of all Co-SimRank scores in \({{{\tilde{\mathbf{S}}}}}\) is exactly the same as that of Li et al.’s SimRank scores in \({{\mathbf {S}}}\) even though the entries in \({{{\tilde{\mathbf{S}}}}}\) can be larger than 1. That is, the ranking of Co-SimRank \({{{\tilde{\mathbf{S}}}}}(*,*)\) is identical to the ranking of Li et al.’s SimRank \({{\mathbf {S}}}(*,*)\).
2.2 Jeh and Widom’s SimRank model
Jeh and Widom’s SimRank model, in matrix notation, can be formulated as
where \({{\mathbf {S}'}}\) is their SimRank similarity matrix; \(\max \{ \mathbf {X}, \mathbf {Y} \}\) is matrix element-wise maximum, i.e., \([\max \{ \mathbf {X}, \mathbf {Y} \}]_{i,j}:=\max \{[\mathbf {X}]_{i,j}, [\mathbf {Y}]_{i,j}\}\).
Remark 1
The recent work by Kusumoto et al. [11] has showed that \({{\mathbf {S}}}\) and \({{\mathbf {S}'}}\) do not produce the same results. Recently, Yu and McCann [28] have showed the subtle difference of the two SimRank models from a semantic perspective, and also justified that Li et al.’s SimRank \({{\mathbf {S}}}\) can capture more pairs of self-intersecting paths that are neglected by Jeh and Widom’s SimRank \({{\mathbf {S}'}}\). The recent work [18] by Rothe and Schütze has demonstrated further that, in real applications such as bilingual lexicon extraction, the ranking of Co-SimRank \({{{\tilde{\mathbf{S}}}}}\) (i.e., the ranking of Li et al.’s SimRank \({{\mathbf {S}}}\)) is more accurate than that of Jeh and Widom’s SimRank \({{\mathbf {S}'}}\) (see [18, Table 4]).
Despite the high precision of Li et al.’s SimRank model, the existing incremental approach of Li et al. [13] for updating SimRank does not always obtain the correct solution \(\mathbf {S}\) to Eq. (1). (Please refer to “Appendix A” [32] for theoretical explanations).
Table 1 lists the notations used in this article.
3 Edge update without node insertions
In this section, we consider edge update that does not accompany new node insertions, i.e., the insertion of new edge (i, j) into \(G=(V,E)\) with \(i \in V\) and \(j \in V\). In this case, the new SimRank matrix \({\tilde{\mathbf{S}}}\) and the old one \(\mathbf {S}\) are of the same size. As such, it makes sense to denote the SimRank change \({\varvec{\Delta }}{} \mathbf{S}\) as \({\tilde{\mathbf{S}}} -\mathbf {S}\).
Below we first introduce the big picture of our main idea and then present rigorous justifications and proofs.
3.1 The main idea
For each edge (i, j) insertion, we can show that \({\varvec{\Delta }}{} \mathbf{Q}\) is a rank-one matrix, i.e., there exist two column vectors \(\mathbf {u},\mathbf {v} \in \mathbb {R}^{n \times 1} \) such that \({\varvec{\Delta }}{} \mathbf{Q} \in \mathbb {R}^{n \times n}\) can be decomposed into the outer product of \(\mathbf {u}\) and \(\mathbf {v}\) as follows:
Based on Eq. (4), we then have an opportunity to efficiently compute \({\varvec{\Delta }}{} \mathbf{S}\), by characterizing it as
where the auxiliary matrix \(\mathbf {M}\in \mathbb {R}^{n \times n}\) satisfies the following rank-one Sylvester equation:
Here, \(\mathbf {u}, \mathbf {w}\) are two obtainable column vectors: \(\mathbf {u}\) can be derived from Eq. (4), and \(\mathbf {w}\) can be described by the old \(\mathbf {Q}\) and \(\mathbf {S}\) (we will provide their exact expressions later after some discussions); and \(\tilde{\mathbf {Q}}=\mathbf {Q} + {\varvec{\Delta }}{} \mathbf{Q}\).
Thus, computing \({\varvec{\Delta }}{} \mathbf{S}\) boils down to solving \(\mathbf {M}\) in Eq. (6). The main advantage of solving \(\mathbf {M}\) via Eq. (6), as compared to directly computing the new scores \(\tilde{\mathbf {S}}\) via SimRank formula
is the high computational efficiency. More specifically, solving \(\tilde{\mathbf {S}}\) via Eq. (7) needs expensive matrix–matrix multiplications, whereas solving \(\mathbf {M}\) via Eq. (6) involves only matrix–vector and vector–vector multiplications, which is a substantial improvement achieved by our observation that \((C \cdot \mathbf {u} \mathbf {w}^\mathrm{T}) \in \mathbb {R}^{n \times n}\) in Eq. (6) is a rank-one matrix, as opposed to the (full) rank- n matrix \((1-C) \cdot \mathbf {I}_n\) in Eq. (7). To further elaborate on this, we can readily convert the recursive forms of Eqs. (6) and (7), respectively, into the series forms:
To compute the sums in Eq. (8) for \(\mathbf {M}\), a conventional way is to memorize \(\mathbf {M}_0 \leftarrow C \cdot \mathbf {u}\cdot {{\mathbf {w}}^\mathrm{T}}\) first (where the intermediate result \(\mathbf {M}_0\) is an \(n \times n\) matrix) and then iterate as
which involves expensive matrix–matrix multiplications (e.g., \({\tilde{\mathbf {Q}}} \cdot \mathbf {M}_{k}\)). In contrast, our method takes advantage of the rank-one structure of \(\mathbf {u}\cdot {{\mathbf {w}}^\mathrm{T}}\) to compute the sums in Eq. (8) for \(\mathbf {M}\), by converting the conventional matrix–matrix multiplications \({\tilde{\mathbf {Q}}} \cdot (\mathbf {u} {{\mathbf {w}}^\mathrm{T}}) \cdot {\tilde{\mathbf {Q}}}^\mathrm{T}\) into only matrix–vector and vector–vector multiplications \(({\tilde{\mathbf {Q}}} \mathbf {u}) \cdot (\tilde{\mathbf {Q}} {{\mathbf {w}}})^\mathrm{T}\). To be specific, we leverage two vectors \({\varvec{\xi }}_{k}, {\varvec{\eta }}_{k}\), and iteratively compute Eq. (8) as
so that matrix–matrix multiplications are safely avoided.
3.2 Describing \(\mathbf {u}, \mathbf {v},\mathbf {w}\) in Eqs. (4) and (6)
To obtain \( \mathbf {u}\) and \(\mathbf {v}\) in Eq. (4) at a low cost, we have the following theorem.
Theorem 1
Given an old digraph \(G=(V,E)\), if there is a new edge (i, j) with \(i \in V\) and \(j \in V\) to be added to G, then the change to \(\mathbf {Q}\) is an \(n \times n\) rank-one matrix, i.e., \({\varvec{\Delta }}{} \mathbf{Q} = \mathbf {u} \cdot \mathbf {v}^\mathrm{T}\), where
\(\square \)
(Please refer to “Appendix B.1” [32] for the proof of Theorem 1, and “Appendix C.2” [32] for an example.)
Theorem 1 suggests that the change \({\varvec{\Delta }}{} \mathbf{Q}\) is an \(n\times n\) rank-one matrix, which can be obtain in only constant time from \(d_j\) and \({{[\mathbf {Q}]}_{j,\star }^\mathrm{T}}\). In light of this, we next describe \(\mathbf {w}\) in Eq. (6) in terms of the old \(\mathbf {Q}\) and \(\mathbf {S}\) such that Eq. (6) is a rank-one Sylvester equation.
Theorem 2
Let \((i,j)_{i \in V, \ j \in V}\) be a new edge to be added to G (resp. an existing edge to be deleted from G). Let \(\mathbf {u}\) and \(\mathbf {v}\) be the rank-one decomposition of \({\varvec{\Delta }}{} \mathbf{Q} = \mathbf {u} \cdot \mathbf {v}^\mathrm{T}\). Then, (i) there exists a vector \(\mathbf {w}=\mathbf {y}+\tfrac{\lambda }{2}\mathbf {u}\) with
such that Eq. (6) is the rank-one Sylvester equation.
(ii) Utilizing the solution \(\mathbf {M}\) to Eq. (6), the SimRank update matrix \({\varvec{\Delta }}{} \mathbf{S}\) can be represented by Eq. (5). \(\square \)
(The proof of Theorem 2 is in “Appendix B.2.” [32])
Theorem 2 provides an elegant expression of \(\mathbf {w}\) in Eq. (6). To be precise, given \(\mathbf {Q}\) and \(\mathbf {S}\) in the old graph G, and an edge (i, j) inserted to G, one can find \(\mathbf {u}\) and \(\mathbf {v}\) via Theorem 1 first, and then resort to Theorem 2 to compute \(\mathbf {w}\) from \(\mathbf {u},\mathbf {v},\mathbf {Q},\mathbf {S}\). Due to the existence of the vector \(\mathbf {w}\), it can be guaranteed that the Sylvester equation (6) is rank-one. Henceforth, our aforementioned method can be employed to iteratively compute \(\mathbf {M}\) in Eq. (8), requiring no matrix–matrix multiplications.
3.3 Characterizing \({\varvec{\Delta }}{} \mathbf{S}\)
Leveraging Theorems 1 and 2, we next characterize the SimRank change \({\varvec{\Delta }}{} \mathbf{S}\).
Theorem 3
If there is a new edge (i, j) with \(i \in V\) and \(j \in V\) to be inserted to G, then the SimRank change \({\varvec{\Delta }}\mathbf{S}\) can be characterized as
where the auxiliary vector \(\varvec{\gamma }\) is obtained as follows:
-
(i)
when \({{d}_{j}}=0\),
$$\begin{aligned} \varvec{\gamma } = \mathbf {Q}\cdot {{[\mathbf {S}]}_{\star ,i}}+\tfrac{1}{2}{{[\mathbf {S}]}_{i,i}}\cdot {{\mathbf {e}}_{j}} \end{aligned}$$(14) -
(ii)
when \({{d}_{j}}>0\),

and the scalar \(\lambda \) can be derived from
\(\square \)
(The proof of Theorem 3 is in “Appendix B.2.” [32])
Theorem 3 provides an efficient method to compute the incremental SimRank matrix \({\varvec{\Delta }}{} \mathbf{S}\), by utilizing the previous information of \(\mathbf {Q}\) and \(\mathbf {S}\), as opposed to [13] that requires to maintain the incremental SVD.
3.4 Deleting an edge \((i,j)_{i \in V, \ j \in V}\) from \(G=(V,E)\)
For an edge deletion, we next propose a Theorem 3-like technique that can efficiently update SimRanks.
Theorem 4
When an edge \((i,j)_{i \in V, \ j \in V}\) is deleted from \(G=(V,E)\), the changes to \(\mathbf {Q}\) is a rank-one matrix, which can be described as \({\varvec{\Delta }}{} \mathbf{Q} = \mathbf {u} \cdot \mathbf {v}^\mathrm{T}\), where
The changes \({\varvec{\Delta }}{} \mathbf{S}\) to SimRank can be characterized as
where the auxiliary vector \(\varvec{\gamma }:=\)

and \(\lambda :={{[\mathbf {S}]}_{i,i}}+\tfrac{1}{C} \cdot {[\mathbf {S}]}_{j,j}-2\cdot {{[\mathbf {Q}]}_{j,\star }}\cdot {{[\mathbf {S}]}_{\star ,i}} - \tfrac{1}{C} +1\). \(\square \)
(The proof of Theorem 4 is in “Appendix B.4.” [32])
3.5 Inc-uSR algorithm
We present our efficient incremental approach, denoted as Inc-uSR (in “Appendix D.1” [32]), that supports the edge insertion without accompanying new node insertions. The complexity of Inc-uSR is bounded by \(O(Kn^2)\) time and \(O(n^2)\) memoryFootnote 5 in the worst case for updating all \(n^2\) pairs of similarities.
(Please refer to “Appendix D.1” [32] for a detailed description of Inc-uSR, and “Appendix C.3” [32] for an example.)
4 Pruning unnecessary node pairs in \({\varvec{\Delta }}{} \mathbf{S}\)
After the SimRank update matrix \({\varvec{\Delta }}{} \mathbf{S}\) has been characterized as a rank-one Sylvester equation, pruning techniques can further skip node pairs with unchanged SimRanks in \({\varvec{\Delta }}{} \mathbf{S}\) (called “unaffected areas”).
4.1 Affected areas in \({\varvec{\Delta }}{} \mathbf{S}\)
We next reinterpret the series \(\mathbf {M}\) in Theorem 3, aiming to identify “affected areas” in \({\varvec{\Delta }}\mathbf{S}\). Due to space limitations, we mainly focus on the edge insertion case of \(d_j>0\). Other cases have the similar results.
By substituting Eq. 15 back into Eq. (13), we can readily split the series form of \(\mathbf {M}\) into three parts:
with the scalar \(\mu :=\frac{\lambda }{2\left( {{d}_{j}}+1 \right) }+\frac{1}{C}-1\).
Intuitively, when edge (i, j) is inserted and \(d_j>0\), Part 1 of \({[\mathbf {M}]}_{a,b}\) tallies the weighted sum of the following new paths for node pair (a, b):

Such paths are the concatenation of four types of sub-paths (as depicted above) associated with four matrices, respectively, \({{[{{{{\tilde{\mathbf{Q}}}}}^{k}}]}_{a,j}}, {{[\mathbf {S}]}_{i,\star }}, {{\mathbf {Q}}^\mathrm{T}},{{[{{({{{{\tilde{\mathbf{Q}}}}}^\mathrm{T}})}^{k}}]}_{\blacktriangle ,b}} \), plus the inserted edge \(j \Leftarrow i\). When such entire concatenated paths exist in the new graph, they should be accommodated for assessing the new SimRank \({[\tilde{\mathbf {S}}]}_{a,b}\) in response to the edge insertion (i, j) because our reinterpretation of SimRank indicates that SimRank counts all the symmetric in-link paths, and the entire concatenated paths can prove to be symmetric in-link paths.
Likewise, Parts 2 and 3 of \({[\mathbf {M}]}_{a,b}\), respectively, tally the weighted sum of the following paths for pair (a, b):


Indeed, when edge (i, j) is inserted, only these three kinds of paths have extra contributions for \(\mathbf {M}\) (therefore for \({\varvec{\Delta }}{} \mathbf{S}\)). As incremental updates in SimRank merely tally these paths, node pairs without having such paths could be safely pruned. In other words, for those pruned node pairs, the three kinds of paths will have “zero contributions” to the changes in \(\mathbf {M}\) in response to edge insertion. Thus, after pruning, the remaining node pairs in G constitute the “affected areas” of \(\mathbf {M}\).
We next identify “affected areas” of \(\mathbf {M}\), by pruning redundant node pairs in G, based on the following.
Theorem 5
For the edge (i, j) insertion, let \({\mathcal {O}}(a)\) and \({\tilde{\mathcal {O}}}(a)\) be the out-neighbors of node a in old G and new \(G\cup \{(i,j)\}\), respectively. Let \(\mathbf {M}_k\) be the kth iterative matrix in Eq. (10), and let

Then, for every iteration \(k=0,1,\ldots \), the matrix \({{\mathbf {M}}_{k}}\) has the following sparse property:

For the edge (i, j) deletion case, all the above results hold except that, in Eq. (21), the conditions \(d_j=0\) and \(d_j>0\) are, respectively, replaced by \(d_j=1\) and \(d_j>1\). \(\square \)
(Please refer to “Appendix B.5” [32] for the proof and intuition of Theorem 5, and “Appendix C.4” [32] for an example.)
Theorem 5 provides a pruning strategy to iteratively eliminate node pairs with a priori zero values in \(\mathbf {M}_k\) (thus in \({\varvec{\Delta }}{} \mathbf{S}\)). Hence, by Theorem 5, when edge (i, j) is updated, we just need to consider node pairs in \(({{{\mathcal {A}}}_{k}}\times {{{\mathcal {B}}}_{k}}) \cup ({{{\mathcal {A}}}_{0}}\times {{{\mathcal {B}}}_{0}})\) for incrementally updating \({\varvec{\Delta }}{} \mathbf{S}\).
4.2 Inc-SR algorithm with pruning
Based on Theorem 5, we provide a complete incremental algorithm, referred to as Inc-SR, by incorporating our pruning strategy into Inc-uSR. The total time of Inc-SR is \(O(K(m+|{\textsf {AFF}}|))\) for K iterations, where \(|{\textsf {AFF}}|:= \text {avg}_{k \in [0,K]} ( |\mathcal{A}_k| \cdot |\mathcal{B}_k|)\) with \(\mathcal{A}_k, \mathcal{B}_k\) in Eq. 22, being the average size of “affected areas” in \(\mathbf {M}_k\) for K iterations.
(Please refer to “Appendix D.2” [32] for Inc-SR algorithm description and its complexity analysis.)
5 Edge update with node insertions
In this section, we focus on the edge update that accompanies new node insertions. Specifically, given a new edge (i, j) to be inserted into the old graph \(G=(V,E)\), we consider the following cases when
-
(C1) \(i \in V\) and \(j \notin V\); (in Sect. 5.1)
-
(C2) \(i \notin V\) and \(j \in V\); (in Sect. 5.2)
-
(C3) \(i \notin V\) and \(j \notin V\). (in Sect. 5.3)
For each case, we devise an efficient incremental algorithm that can support new node insertions and can accurately update only “affected areas” of SimRanks.
Remark 2
Let \(n=|V|\), without loss of generality, it can be tacitly assumed that
-
(a)
In case (C1), new node \(j \notin V\) is indexed by \((n+1)\);
-
(b)
In case (C2), new node \(i \notin V\) is indexed by \((n+1)\);
-
(c)
In case (C3), new nodes \(i \notin V\) and \(j \notin V\) are indexed by \((n+1)\) and \((n+2)\), respectively.
5.1 Inserting an edge (i, j) with \(i \in V\) and \(j \notin V\)
In this case, the inserted new edge (i, j) accompanies the insertion of a new node j. Thus, the size of the new SimRank matrix \({\tilde{\mathbf{S}}}\) is different from that of the old \(\mathbf {{S}} \). As a result, we cannot simply evaluate the changes to \(\mathbf {{S}} \) by adopting \({\tilde{\mathbf{S}}} -\mathbf {S}\) as we did in Sect. 3.
To resolve this problem, we introduce the block matrix representation of new matrices for edge insertion. Firstly, when a new edge \((i,j)_{i \in V, j \notin V}\) is inserted to G, the new transition matrix \({\tilde{\mathbf{Q}}}\) can be described as

Intuitively, \({\tilde{\mathbf{Q}}}\) is formed by bordering the old \(\mathbf {{Q}}\) by 0s except \([{\tilde{\mathbf{Q}}}]_{j,i}=1\). Utilizing this block structure of \({\tilde{\mathbf{Q}}}\), we can obtain the new SimRank matrix, which exhibits a similar block structure, as shown below:
Theorem 6
Given an old digraph \(G=(V,E)\), if there is a new edge (i, j) with \(i \in V\) and \(j \notin V\) to be inserted, then the new SimRank matrix becomes

where \(\mathbf {S} \in \mathbb {R}^{n \times n}\) is the old SimRank matrix of G. \(\square \)
Proof
We substitute the new \({\tilde{\mathbf{Q}}}\) in Eq. (23) back into the SimRank equation \({\tilde{\mathbf{S}}}=C \cdot {\tilde{\mathbf{Q}}} \cdot {\tilde{\mathbf{S}}} \cdot {{{\tilde{\mathbf{Q}}}}^\mathrm{T}}+(1-C) \cdot {{\mathbf {I}}_{n+1}}\):

By expanding the right-hand side, we can obtain

The above block matrix equation implies that
Due to the uniqueness of \(\mathbf {S}\) in Eq. (1), it follows that
Thus, we have
Combining all blocks of \({{{\tilde{\mathbf{S}}}}}\) together yields Eq. 24. \(\square \)
Theorem 6 provides an efficient incremental way of computing the new SimRank matrix \({\tilde{\mathbf{S}}}\) for unit insertion of the case (C1). Precisely, the new \({\tilde{\mathbf{S}}}\) is formed by bordering the old \(\mathbf {{S}}\) by the auxiliary vector \(\mathbf {y}\). To obtain \(\mathbf {y}\) (and thereby \({\tilde{\mathbf{S}}}\)), we just need use the ith column of \(\mathbf {{S}}\) with one matrix–vector multiplication \((\mathbf {Q}{{[\mathbf {S}]}_{\star ,i}})\). Thus, the total cost of computing new \({\tilde{\mathbf{S}}}\) requires O(m) time, as illustrated in Algorithm 1.
Example 2
Consider the citation digraph G in Fig. 3. If the new edge (i, p) with new node p is inserted to G, the new \({\tilde{\mathbf{S}}}\) can be updated from the old \(\mathbf {{S}}\) as follows:
According to Theorem 6, since \(C=0.8\) and

it follows that

\(\square \)

5.2 Inserting an edge (i, j) with \(i \notin V\) and \(j \in V\)
We now focus on the case (C2), the insertion of an edge (i, j) with \(i \notin V\) and \(j \in V\). Similar to the case (C1), the new edge accompanies the insertion of a new node i. Hence, \({\tilde{\mathbf{S}}} -\mathbf {S}\) makes no sense.
However, in this case, the dynamic computation of SimRank is far more complicated than that of the case (C1), in that such an edge insertion not only increases the dimension of the old transition matrix \(\mathbf {{Q}}\) by one, but also changes several original elements of \(\mathbf {{Q}}\), which may recursively influence SimRank similarities. Specifically, the following theorem shows, in the case (C2), how \(\mathbf {{Q}}\) changes with the insertion of an edge \((i,j)_{i \notin V, j \in V}\).
Theorem 7
Given an old digraph \(G=(V,E)\), if there is a new edge (i, j) with \(i \notin V\) and \(j \in V\) to be added to G, then the new transition matrix can be expressed as

where \(\mathbf {Q}\) is the old transition matrix of G. \(\square \)
Proof
When edge (i, j) with \(i \notin V\) and \(j \in V\) is added, there will be two changes to the old \(\mathbf {Q}\):
-
(i)
All nonzeros in \({{[\mathbf {Q}]}_{j,\star }}\) are updated from \(\tfrac{1}{d_j}\) to \(\tfrac{1}{d_j+1}\):
$$\begin{aligned} {{[{\hat{\mathbf{Q}}}]}_{j,\star }} = \tfrac{{{d}_{j}}}{{{d}_{j}}+1} {{[\mathbf {Q}]}_{j,\star }} = {{[\mathbf {Q}]}_{j,\star }} - \tfrac{1}{{{d}_{j}}+1} {{[\mathbf {Q}]}_{j,\star }}. \end{aligned}$$(26) -
(ii)
The size of the old \(\mathbf {{Q}}\) is added by 1, with new entry \({{[\tilde{\mathbf {Q}}]}_{j,i}} = \tfrac{1}{d_j+1}\) in the bordered areas and 0s elsewhere:
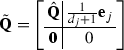 (27)
(27)
\(\square \)
Theorem 7 exhibits a special structure of the new \({{\tilde{\mathbf{Q}}}}\): it is formed by bordering \({{\hat{\mathbf{Q}}}}\) by 0s except \([{{\tilde{\mathbf{Q}}}}]_{j,i}=\tfrac{1}{d_j+1}\), where \({{\hat{\mathbf{Q}}}}\) is a rank-one update of the old \({\mathbf {{Q}}}\). The block structure of \({{\tilde{\mathbf{Q}}}}\) inspires us to partition the new SimRank matrix \({{\tilde{\mathbf{S}}}}\) conformably into the similar block structure:

To determine each block of \({\tilde{\mathbf{S}}}\) with respect to the old \(\mathbf {S}\), we next present the following theorem.
Theorem 8
If there is a new edge (i, j) with \(i \notin V\) and \(j \in V\) to be added to the old digraph \(G=(V,E)\), then there exists a vector
such that the new SimRank matrix \({\tilde{\mathbf{S}}}\) is expressible as

where \(\mathbf {S}\) is the old SimRank of G, and \({\varvec{\Delta }}{{{{\tilde{\mathbf{S}}}}}_{\mathbf {11}}}\) satisfies the rank-two Sylvester equation:
with \({\hat{\mathbf{Q}}}\) being defined by Theorem 7. \(\square \)
Proof
We plug \({\tilde{\mathbf{Q}}}\) of Eq. 25 into the SimRank formula:
which produces

By using block matrix multiplications, the above equation can be simplified as


Block-wise comparison of both sides of Eq. (31) yields
Combing the above equations with Eq. (32) produces
Applying \({{{\tilde{\mathbf{S}}}}_{\mathbf {11}}}=\mathbf {S}+{\varvec{\Delta }}{{{\tilde{\mathbf{S}}}}_{\mathbf {11}}}\) and \(\mathbf {S}=C \mathbf {Q} \mathbf {S} {{\mathbf {Q}}^\mathrm{T}}+(1-C) {{\mathbf {I}}_{n}}\) to Eq. (33) and rearranging the terms, we have
with \({\alpha }\) and \(\mathbf {y}\) being defined by Eq. (28). \(\square \)
Theorem 8 implies that, in the case (C2), after a new edge (i, j) is inserted, the new SimRank matrix \({\tilde{\mathbf{S}}}\) takes an elegant diagonal block structure: the upper-left block of \({\tilde{\mathbf{S}}}\) is perturbed by \({\varvec{\Delta }}\tilde{\mathbf{S}}_{\mathbf{11}}\) which is the solution to the rank-two Sylvester equation (30); the lower-right block of \({\tilde{\mathbf{S}}}\) is a constant \((1-C)\). This structure of \({\tilde{\mathbf{S}}}\) suggests that the inserted edge \((i,j)_{i \notin V, j \in V}\) only has a recursive impact on the SimRanks with pairs \((x,y) \in V \times V\), but with no impacts on pairs \((x,y) \in (V \times \{i\}) \cup (\{i\} \times V)\). Thus, our incremental way of computing the new \({\tilde{\mathbf{S}}}\) will focus on the efficiency of obtaining \({\varvec{\Delta }}\tilde{\mathbf{S}}_{\mathbf{11}}\) from Eq. (30). Fortunately, we notice that \({\varvec{\Delta }}\tilde{\mathbf{S}}_{\mathbf{11}}\) satisfies the rank-two Sylvester equation, whose algebraic structure is similar to that of \({\varvec{\Delta }}{} \mathbf{S}\) in Eqs. (5) and (6) (in Sect. 3). Hence, our previous techniques to compute \({\varvec{\Delta }}{} \mathbf{S}\) in Eqs. (5) and (6) can be analogously applied to compute \({\varvec{\Delta }}\tilde{\mathbf{S}}_{\mathbf{11}}\) in Eq. (30), thus eliminating costly matrix–matrix multiplications, as will be illustrated in Algorithm 2.
One disadvantage of Theorem 8 is that, in order to get the auxiliary vector \(\mathbf {z}\) for evaluating \({\tilde{\mathbf{S}}}\), one has to memorize the entire old matrix \(\mathbf {S}\) in Eq. (28). In fact, we can utilize the technique of rearranging the terms of the SimRank Eq. (1) to characterize \(\mathbf {Q} \mathbf {S} {{[\mathbf {Q}]}_{j,\star }^\mathrm{T}}\) in terms of only one vector \([\mathbf {S}]_{\star ,j}\) so as to avoid memorizing the entire \(\mathbf {S}\), as shown below.
Theorem 9
The auxiliary matrix \({\varvec{\Delta }}{{{{\tilde{\mathbf{S}}}}}_{\mathbf {11}}}\) in Theorem 8 can be represented as
where \({\hat{\mathbf{Q}}}\) is defined by Theorem 7 and

and \(\mathbf {S}\) is the old SimRank matrix of G. \(\square \)
Proof
We multiply the SimRank equation by \({{\mathbf {e}}_{j}}\) to get
Combining this with \(\mathbf {y}=\mathbf {QS}{{[\mathbf {Q}]}_{j,\star }^\mathrm{T}}\) in Eq. (28) produces
Plugging these results into Eq. (28), we can get Eq. 35.
Also, the recursive form of \({\varvec{\Delta }}{{{\tilde{\mathbf{S}}}}_{\mathbf {11}}}\) in Eq. (30) can be converted into the following series:
with \(\mathbf {M}\) being defined by Eq. (34). \(\square \)
For edge insertion of the case (C2), Theorem 9 gives an efficient method to compute the update matrix \({\varvec{\Delta }}{{{{\tilde{\mathbf{S}}}}}_{\mathbf {11}}}\). We note that the form of \({\varvec{\Delta }}{{{{\tilde{\mathbf{S}}}}}_{\mathbf {11}}}\) in Eq. (34) is similar to that of \({\varvec{\Delta }}{{{{\tilde{\mathbf{S}}}}}}\) in Eq. (13). Thus, similar to Theorem 3, the follow method can be applied to compute \(\mathbf {M}\) so as to avoid matrix–matrix multiplications.
In Algorithm 2, we present the edge insertion of our method for the case (C2) to incrementally update new SimRank scores. The total complexity of Algorithm 2 is \(O(Kn^2)\) time and \(O(n^2)\) memory in the worst case for retrieving all \(n^2\) pairs of scores, which is dominated by Line 8. To reduce its computational time further, the similar pruning techniques in Sect. 4 can be applied to Algorithm 2. This can speed up the computational time to \(O(K(m+|{\textsf {AFF}}|))\), where \(|{\textsf {AFF}}|\) is the size of “affected areas” in \({\varvec{\Delta }}{} \mathbf{S}_{11}\).
Example 3
Consider the citation digraph G in Fig. 4. If the new edge (p, j) with new node p is inserted to G, the new \({\tilde{\mathbf{S}}}\) can be incrementally derived from the old \(\mathbf {S}\) as follows:
First, we obtain \({\varvec{\Delta }}{{{{\tilde{\mathbf{S}}}}}_{\mathbf {11}}}\) according to Theorem 9. Note that \(C=0.8\), \(d_j=2\), and the old SimRank scores

It follows from Eq. 35 that the auxiliary vector

Utilizing \(\mathbf {z}\), we can obtain \(\mathbf {M}\) from Eq. (34). Thus, \({\varvec{\Delta }}{{{\tilde{\mathbf{S}}}}_{\mathbf {11}}}\) can be computed from \(\mathbf {M}\) as

Next, by Theorem 8, we obtain the new SimRank

which is partially illustrated in Fig. 4. \(\square \)

5.3 Inserting an edge (i, j) with \(i \notin V\) and \(j \notin V\)
We next focus on the case (C3), the insertion of an edge (i, j) with \(i \notin V\) and \(j \notin V\). Without loss of generality, it can be tacitly assumed that nodes i and j are indexed by \(n+1\) and \(n+2\), respectively. In this case, the inserted edge (i, j) accompanies the insertion of two new nodes, which can form another independent component in the new graph.
In this case, the new transition matrix \({\tilde{\mathbf{Q}}}\) can be characterized as a block diagonal matrix

With this structure, we can infer that the new SimRank matrix \({\tilde{\mathbf{S}}}\) takes the block diagonal form as

This is because, after a new edge \((i,j)_{i \notin V, j \notin V}\) is added, all node pairs \((x,y) \in (V \times \{i,j\} \cup \{i,j\} \times V)\) have zero SimRank scores since there are no connections between nodes x and y. Besides, the inserted edge (i, j) is an independent component that has no impact on s(x, y) for \(\forall (x,y)\in V \times V\). Hence, the submatrix \({\hat{\mathbf{S}}}\) of the new SimRank matrix can be derived by solving the equation:
This suggests that, for unit insertion of the case (C3), the new SimRank matrix becomes

Algorithm 3 presents our incremental method to obtain the new SimRank matrix \({\tilde{\mathbf{S}}}\) for edge insertion of the case (C3), which requires just O(1) time.

6 Batch updates
In this section, we consider the batch updates problem for incremental SimRank, i.e., given an old graph \(G=(V,E)\) and a sequence of edges \(\Delta G\) to be updated to G, the retrieval of new SimRank scores in \(G\oplus \Delta G\). Here, the set \(\Delta G\) can be mixed with insertions and deletions:

where \((i_q, j_q)\) is the qth edge in \(\Delta G\) to be inserted into (if \({\textsf {op}}_q =\)“\(+\)”) or deleted from (if \({\textsf {op}}_q =\)“−”) G.
The straightforward approach to this problem is to update each edge of \(\Delta G\) one by one, by running a unit update algorithm for \(|\Delta G|\) times. However, this would produce many unnecessary intermediate results and redundant updates that may cancel out each other.
Example 4
Consider the old citation graph G in Fig. 5, and a sequence of edge updates \(\Delta G\) to G:

We notice that, in \(\Delta G\), the edge insertion \((b,h,+)\) can cancel out the edge deletion \((b,h,-)\). Similarly, \((l,f,+)\) can cancel out \((l,f,-)\). Thus, after edge cancelation, the net update of \(\Delta G\), denoted as \(\Delta G_{\mathrm{net}}\), is
\(\square \)

Example 4 suggests that a portion of redundancy in \(\Delta G\) arises from the insertion and deletion of the same edge that may cancel out each other. After cancelation, it is easy to verify that
To obtain \(\Delta G_{\mathrm{net}}\) from \(\Delta G\), we can readily use hashing techniques to count occurrences of updates in \(\Delta G\). More specifically, we use each edge of \(\Delta G\) as a hash key, and initialize each key with zero count. Then, we scan each edge of \(\Delta G\) once, and increment (resp. decrement) its count by one each time an edge insertion (resp. deletion) appears in \(\Delta G\). After all edges in \(\Delta G\) are scanned, the edges whose counts are nonzeros make a net update \(\Delta G_{\mathrm{net}}\). All edges in \(\Delta G_{\mathrm{net}}\) with \(+1\) (resp. \(-1\)) counts make a net insertion update \(\Delta G_{\mathrm{net}}^{+}\) (resp. a net deletion update \(\Delta G_{\mathrm{net}}^{-}\)). Clearly, we have
Having reduced \(\Delta G\) to the net edge updates \(\Delta G_{\mathrm{net}}\), we next merge the updates of “similar sink edges” in \(\Delta G_{\mathrm{net}}\) to speedup the batch updates further.
We first introduce the notion of “similar sink edges.”
Definition 1
Two distinct edges (a, c) and (b, c) are called “similar sink edges” w.r.t. node c if they have a common end node c that both a and b point to. \(\square \)
“Similar sink edges” is introduced to partition \(\Delta G_{\mathrm{net}}\). To be specific, we first sort all the edges \(\{(i_p,j_p)\}\) of \(\Delta G_{\mathrm{net}}^{+}\) (resp. \(\Delta G_{\mathrm{net}}^{-}\)) according to its end node \(j_p\). Then, the “similar sink edges” w.r.t. node \(j_p\) form a partition of \(\Delta G_{\mathrm{net}}^{+}\) (resp. \(\Delta G_{\mathrm{net}}^{-}\)). For each block \(\{(i_{p_k},j_p)\}\) in \(\Delta G_{\mathrm{net}}^{+}\), we next split it further into two sub-blocks according to whether its end node \(i_{p_k}\) is in the old V. Thus, after partitioning, each block in \(\Delta G_{\mathrm{net}}^{+}\) (resp. \(\Delta G_{\mathrm{net}}^{-}\)), denoted as \( \{(i_1,j), \ (i_2,j), \ldots , \ (i_{\delta },j)\}, \) falls into one of the following cases:
-
(C0) \(i_1 \in V, \ i_2 \in V, \ \ldots , i_{\delta } \in V\) and \(j \in V\);
-
(C1) \(i_1 \in V, \ i_2 \in V, \ \ldots , i_{\delta } \in V\) and \(j \notin V\);
-
(C2) \(i_1 \notin V, \ i_2 \notin V, \ \ldots , i_{\delta } \notin V\) and \(j \in V\);
-
(C3) \(i_1 \notin V, \ i_2 \notin V, \ \ldots , i_{\delta } \notin V\) and \(j \notin V\).
Example 5
Let us recall \(\Delta G_{\mathrm{net}}\) derived by Example 4, in which \(\Delta G_{\mathrm{net}} = \Delta G_{\mathrm{net}}^{+} \cup \Delta G_{\mathrm{net}}^{-}\) with
We first partition \(\Delta G_{\mathrm{net}}^{+}\) by “similar sink edges” into

In the first block of \(\Delta G_{\mathrm{net}}^{+}\), since the nodes \(q \notin V\), \(j \in V\), and \(k \in V\), we will partition this block further into \(\{ (q,i,+)\} \cup \{ (j,i,+), (k,i,+) \}\). Eventually,

\(\square \)
The main advantage of our partitioning approach is that, after partition, all the edge updates in each block can be processed simultaneously, instead of one by one. To elaborate on this, we use case (C0) as an example, i.e., the insertion of \(\delta \) edges \(\{(i_1,j), \ (i_2,j), \ \ldots , \ (i_{\delta },j)\}\) into \(G=(V,E)\) when \(i_1 \in V, \ldots , i_{\delta } \in V\), and \(j \in V\). Analogous to Theorem 1, one can readily prove that, after such \(\delta \) edges are inserted, the changes \({\varvec{\Delta }}{} \mathbf{Q}\) to the old transition matrix is still a rank-one matrix that can be decomposed as \({\tilde{\mathbf{Q}}} = \mathbf {Q}+\mathbf {u} \cdot \mathbf {v}^\mathrm{T} \ \text { with } \)

where \({\mathbf {e}}_{I}\) is an \(n \times 1\) vector with its entry \([{\mathbf {e}}_{I}]_x=1\) if \(x \in I\triangleq \{i_1,i_2, \ldots , i_{\delta }\}\), and \([{\mathbf {e}}_{I}]_x=0\) if \(x \notin V\). Since the rank-one structure of \({\varvec{\Delta }}{} \mathbf{Q}\) is preserved for updating \(\delta \) edges, Theorem 2 still holds under the new settings of \(\mathbf {u}\) and \(\mathbf {v}\) for batch updates. Therefore, the changes \({\varvec{\Delta }}{} \mathbf{S}\) to the SimRank matrix in response to \(\delta \) edges insertion can be represented as a similar formulation to Theorem 3, as illustrated in the first row of Table 2. Similarly, we can also extend Theorems 6–9 in Sect. 5 to support batch updates of \(\delta \) edges for other cases (C1)–(C3) that accompany new node insertions. Table 2 summarizes the new \(\mathbf {Q}\) and \(\mathbf {S}\) in response to such batch edge updates of all the cases. When \(\delta =1\), these batch update results in Table 2 can be reduced to the unit update results of Theorems 1–9.

Algorithm 4 presents an efficient batch updates algorithm, Inc-bSR, for dynamical SimRank computation. The actual computational time of Inc-bSR depends on the input parameter \(\Delta G\) since different update types in Table 2 would result in different computational time. However, we can readily show that Inc-bSR is superior to the \(|\Delta G|\) executions of the unit update algorithm, because Inc-bSR can process the “similar sink updates” of each block simultaneously and can cancel out redundant updates. To clarify this, let us assume that \(|\Delta G_{\mathrm{net}}|\) can be partitioned into |B| blocks, with \(\delta _t\) denoting the number of edge updates in tth block. In the worst case, we assume that all edge updates happen to be the most time-consuming case (C0) or (C2). Then, the total time for handling \(|\Delta G|\) updates is bounded by
Note that \(|B| \le |\Delta G_{\mathrm{net}}|\), in general \(|B| \ll |\Delta G_{\mathrm{net}}|\). Thus, Inc-bSR is typically much faster than the \(|\Delta G|\) executions of the unit update algorithm that is bounded by \(O\big ( |\Delta G| K(nd+\Delta G+|{\textsf {AFF}}|) \big )\).
Example 6
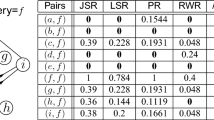
Recall from Example 4 that a sequence of edge updates \(\Delta G\) to the graph \(G=(V,E)\) in Fig. 5. We want to compute new SimRank scores in \(G \oplus \Delta G\).
First, we can use hashing method to obtain the net update \(\Delta G_{\mathrm{net}}\) from \(\Delta G\), as shown in Example 4.
Next, by Example 5, we can partition \(\Delta G_{\mathrm{net}}\) into
Then, for each block, we can apply the formulae in Table 2 to update all edges simultaneously in a batch fashion. The results are partially depicted as follows:
Node | \(\textsf {sim}_\textsf {old}\) | \((f,b,-)\) | \((q,i,+)\) | \((j,i,+)\) | \((p,f,+)\) |
|---|---|---|---|---|---|
Pairs | in G | \((k,i,+)\) | \((r,f,+)\) | ||
(a, b) | 0.0745 | 0.0809 | 0.0809 | 0.0809 | 0.0809 |
(a, i) | 0 | 0 | 0 | 0.0340 | 0.0340 |
(b, i) | 0 | 0 | 0 | 0.0340 | 0.0340 |
(f, i) | 0.2464 | 0.2464 | 0.1232 | 0.1032 | 0.0516 |
(f, j) | 0.2064 | 0.2064 | 0.2064 | 0.2064 | 0.1032 |
(g, h) | 0.128 | 0.128 | 0.128 | 0.128 | 0.128 |
(g, k) | 0.128 | 0.128 | 0.128 | 0.128 | 0.128 |
(h, k) | 0.288 | 0.288 | 0.288 | 0.288 | 0.288 |
(i, j) | 0.3104 | 0.3104 | 0.1552 | 0.1552 | 0.1552 |
(l, m) | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 |
(l, n) | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 |
(m, n) | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 |
The column “\((q,i,+)\)” represents the updated SimRank scores after the edge (q, i) is added to \(G \oplus \{(f,b,-)\} \). The last column is the new SimRanks in \(G \oplus \Delta G\). \(\square \)
7 Memory efficiency
In previous sections, our main focus was devoted to speeding up the computational time of incremental SimRank. However, for updating all pairs of SimRank scores, the memory requirement for Algorithms 1–4 remains at \(O(n^2)\) since they need to store all \((n^2)\) pairs of old SimRank \(\mathbf {S}\) into memory, which hinders its scalability on large graphs. We call Algorithms 1–4 in-memory algorithms.
In this section, we propose a novel scalable method based on Algorithms 1–4 for dynamical SimRank search, which updates all pairs of SimRanks column by column using only \(O(Kn+m)\) memory, with no need to store all \((n^2)\) pairs of old SimRank \(\mathbf {S}\) into memory, and with no loss of accuracy.
Let us first analyze the \(O(n^2)\) memory requirement for Algorithms 1–4 in Sects. 3–5. We notice that there are two factors dominating the original \(O(n^2)\) memory: (1) the storage of the entire \(n \times n\) old SimRank matrix \(\mathbf {S}\), and (2) the computation of \(\mathbf {M}_k\) from one outer product. For example, in Inc-uSR (in “Appendix D.1” [32]), Lines 3, 4, 6, 9, 15 need to get elements from old \(\mathbf {S}\) (see Table 3); Lines 10, 14, 15 require to store \( n \times n\) entries of matrix \(\mathbf {M}_k\) (see Table 4). Indeed, the storage of \(\mathbf {S}\) and \(\mathbf {M}_k\) are the main obstacles to the scalability of our in-memory algorithms on large graphs, resulting in \(O(n^2)\) memory space. Apart from these lines, the memory required for the remaining steps of Inc-uSR is O(m), dominated by (a) the storage of sparse matrix \(\mathbf {Q}\) and (b) sparse matrix–vector products.
To overcome the bottleneck of the \(O(n^2)\) memory, our main idea is to update all pairs of \(\mathbf {S}\) in a column-by-column style, with no need to store the entire \(\mathbf {S}\) and \(\mathbf {M}_k\). Specifically, we update \(\mathbf {S}\) by updating each column \([\mathbf {{S}}]_{\star ,x} \ (\forall x=1,2,\ldots )\) of \(\mathbf {S}\) individually. Let us rewrite Line 15 of Table 3 into the column-wise style:
Applying the following facts
into Eq. (36) produces
This implies that, to compute one column of \({{\varvec{\Delta }}{} \mathbf{S}}\), we only need prepare one row and one column of \(\mathbf {M}_{K}\). To compute only the xth row and xth column of \(\mathbf {M}_{K}\), there are two challenges: (1) From Line 10 of Table 3, we notice that \(\mathbf {M}_{K}\) is derived from the auxiliary vector \(\varvec{\gamma }\), and \(\varvec{\gamma }\) depends on the ith and jth column of old \({\mathbf {S}}\) according to lines 3, 4, 6, 9 of Table 3. Since the update edge (i, j) can be arbitrary, it is hard to determine which columns of old \({\mathbf {S}}\) will be used in future. Thus, all our in-memory algorithms in Sect. 5 prepare \(n \times n\) elements of \({\mathbf {S}}\) into memory, leading to \(O(n^2)\) memory. (2) According to lines 10, 14, 15 of Table 4, it also requires \(O(n^2)\) memory to iteratively compute \(\mathbf {M}_{K}\). It is not easy to use just linear memory for iteratively computing only one row and one column of \(\mathbf {M}_{K}\). In the next two subsections, we will address these two challenges, respectively.
7.1 Avoid storing \(n \times n\) elements of old \(\mathbf {S}\)


Our above analysis imply that, to compute each column \({[{{\varvec{\Delta }}{} \mathbf{S}}]}_{\star , x}\), we only need prepare two columns information (ith and jth) from old \(\mathbf {S}\). Since the update edge (i, j) can be arbitrary, there are no prior knowledge which ith and jth columns in old \(\mathbf {S}\) will be used. As opposed to Algorithms 1–4 that memorize all \((n^2)\) pairs of old \(\mathbf {S}\), we use the following scalable method to compute only the ith and jth columns of old \(\mathbf {S}\) on demand in linear memory. Specifically, based on our previous work [27] on partial-pairs SimRank retrieval, we can readily verify that the following iterations will yield \([\mathbf {S}]_{\star ,i}\) and \([\mathbf {S}]_{\star ,j}\) in just \(O(Kn+m)\) memory.

Next, \([\mathbf {S}]_{i,i}\) is obtained from the ith element of \([\mathbf {S}]_{\star ,i}\), and \([\mathbf {S}]_{j,j}\) from the jth element of \([\mathbf {S}]_{\star ,j}\). Having prepared \([\mathbf {S}]_{\star ,i}, [\mathbf {S}]_{\star ,j}, [\mathbf {S}]_{i,i}\), and \( [\mathbf {S}]_{j,j}\), we follow Lines 3, 4, 6, 9 of Table 3 to derive the vector \(\varvec{\gamma }\) in linear memory. In addition, since Line 15 of Table 3 can be computed column-wisely via Eq. (37). Throughout all lines in Table 3, we do not need store \(n^2\) pairs of old \(\mathbf {S}\) in memory. However, \(O(n^2)\) memory is still required to store \(\mathbf {M}_k\). In the next subsection, we will show how to avoid \(O(n^2)\) memory to compute \(\mathbf {M}_k\).
7.2 Compute \({[\mathbf {M}_K]}_{\star , x}\) and \({[\mathbf {M}_K]}_{x, \star }\) in linear memory
Using \(\varvec{\gamma }\), we next devise our method based on Table 4, aiming to use linear memory to compute each column \({[\mathbf {M}_K]}_{\star , x}\) and each row \({[\mathbf {M}_K]}_{x, \star }\) for Eq. (37). In Table 4, our key observation is that \(\mathbf {M}_k\) is the summation of the outer product of two vectors. Due to this structure, instead of using \(O(n^2)\) memory to store \(\mathbf {M}_k\), we can use only O(n) memory to compute \({[\mathbf {M}_K]}_{\star , x}\) and \({[\mathbf {M}_K]}_{x,\star }\). Specifically, we can compute Lines 10 and 14 of Table 4 in a column-wise style for \({[\mathbf {M}_K]}_{\star , x}\) as follows:

and in a row-wise style for \({[\mathbf {M}_K]}_{x,\star }\) as follows:

Figure 6 pictorially visualizes the column-wise computation of \({[{\mathbf {M}}_{K}]}_{\star , x }\). Having computed \({[{\mathbf {M}}_{K}]}_{\star , x }\) and \({[{\mathbf {M}}_{K}]}_{x, \star }\), we can use Eq. (37) to derive the column \({[{{\varvec{\Delta }}{} \mathbf{S}}]}_{\star , x}\) of \({{\varvec{\Delta }}{} \mathbf{S}}\).
The main advantage of our method is that, throughout the entire updating process, we need not store \(n \times n\) pairs of \(\mathbf {M}_k\) and \(\mathbf {S}\), and thereby, significantly reduce the memory usage from \(O(n^2)\) to \(O(Kn+m)\). In addition to the insertion case (C0), our memory-efficient methods are applicable to other insertion cases in Sect. 5.1. The complete algorithm, denoted as Inc-SR-All-P, is described in Algorithm 5. Inc-SR-All-P is a memory-efficient version of Algorithms 1–4. It includes a procedure PartialSim that allows us to compute two columns information of old \(\mathbf {S}\) on demand in linear memory, rather than store \(n^2\) pairs of old \(\mathbf {S}\) in memory. In response to each edge update (i, j), once the two old columns \(\mathbf {S}_{\star ,i}\) and \(\mathbf {S}_{\star ,j}\) are computed via PartialSim for updating the xth column \([{\varvec{\Delta }}{} \mathbf{S}]_{\star ,x}\), they can be memorized in only O(n) memory and reused later to compute another yth column \([{\varvec{\Delta }}{} \mathbf{S}]_{\star ,y}\) in response to the edge update (i, j).
Correctness. Inc-SR-All-P correctly returns similarity. It consists of four update cases: lines 6–22 for Case (C0), lines 23–30 for Case (C1), lines 31–45 for Case (C2), and lines 46–54 for Case (C3). The correctness of each case can be verified by Theorems 3, 6, 8, and 9, respectively. For instance, to verify the correctness for Case (C0), we apply successive substitution to for-loop in lines 14–21, which produces the following result:
This is consistent with Eq. (36), implying that our memory-efficient method does not compromise any accuracy for scalability.

It is worth mentioning that Inc-SR-All-P can be also combined with our batch updating method in Sect. 6. This will speed up the dynamical update of SimRank further, with \(O(n(\max _{t=1}^{|B|}\delta _t) + m + Kn)\) memory. Here \(O(n\delta _t)\) memory is needed to store \(\delta _t\) columns of \(\mathbf {S}\) when \([\mathbf {S}]_{\star ,I}\) is required for processing the tth block.
8 Experimental evaluation
In this section, we present a comprehensive experimental study on real and synthetic datasets, to demonstrate (i) the fast computational time of Inc-SR to incrementally update SimRanks on large time-varying networks, (ii) the pruning power of Inc-SR that can discard unnecessary incremental updates outside “affected areas”; (iii) the exactness of Inc-SR, as compared with Inc-SVD; (iv) the high efficiency of our complete scheme that integrates Inc-SR with Inc-uSR-C1, Inc-uSR-C2, Inc-uSR-C3 to support link updates that allow new node insertions; (v) the fast computation time of our batch update algorithm Inc-bSR against the unit update method Inc-SR; (vi) the scalability of our memory-efficient algorithm Inc-SR-All-P in Sect. 7 on million-scale large graphs for dynamical updates; (vii) the performance comparison between Inc-SR-All-P and LTSF in terms of computational time, memory space, and top-k exactness; (viii) the average updating time and memory usage of Inc-SR-All-P for each case of edge updates.
8.1 Experimental settings
Datasets. We adopt both real and synthetic datasets. The real datasets include small-scale (DBLP and CitH), medium-scale (YouTu, WebB and WebG), and large-scale graphs (CitP, SocL, UK05, and IT04). Table 5 summarizes the description of these datasets.
(Please refer to “Appendix E” [32] for details.)
To generate synthetic graphs and updates, we adopt GraphGen Footnote 6 generation engine. The graphs are controlled by (a) the number of nodes |V|, and (b) the number of edges |E|. We produce a sequence of graphs that follow the linkage generation model [7]. To control graph updates, we use two parameters simulating real evolution: (a) update type (edge/node insertion or deletion), and (b) the size of updates \(|\Delta G|\).
Algorithms. We implement the following algorithms: (a) Inc-SVD, the SVD-based link-update algorithm [13]; (b) Inc-uSR, our incremental method without pruning; (c) Batch, the batch SimRank method via fine-grained memorization [24]; (d) Inc-SR, our incremental method with pruning power but not supporting node insertions; (e) Inc-SR-All, our complete enhanced version of Inc-SR that allows node insertions by incorporating Inc-uSR-C1, Inc-uSR-C2, and Inc-uSR-C3; (f) Inc-bSR, our batch incremental update version of Inc-SR; (g) Inc-SR-All-P, our memory-efficient version of Inc-SR-All that dynamically computes the SimRank matrix column by column without the need to store all pairs of old similarities; (h) LTSF, the log-based implementation of the existing competitor, TSF [20], which supports dynamic SimRank updates for top-k querying.
Parameters. We set the damping factor \(C=0.6\), as used in [9]. By default, the total number of iterations is set to \(K=15\) to guarantee accuracy \({C}^{K} \le 0.0005\) [16]. On CitH and YouTu, we set \(K=10\); On large graphs (CitP, SocL, UK05, and IT04), we set \(K=5\). The target rank r for Inc-SVD is a speed-accuracy trade-off, we set \(r=5\) in our time evaluation since, as shown in the experiments of [13], the highest speedup is achieved when \(r=5\). In our exactness evaluation, we shall tune this value. For LTSF algorithm, we set the number of one-way graphs \(R_g = 100\), and the number of samples at query time \(R_q=20\), as suggested in [20].
All the algorithms are implemented in Visual C++ and MATLAB. For small-scale graphs, we use a machine with an Intel Core 2.80GHz CPU and 8GB RAM. For medium- and large-scale graphs, we use a processor with Intel Core i7-6700 3.40GHz CPU and 64GB RAM.
8.2 Experimental results
8.2.1 Time efficiency of Inc-SR and Inc-uSR
We first evaluate the computational time of Inc-SR and Inc-uSR against Inc-SVD and Batch on real datasets.
Note that, to favor Inc-SVD that only works on small graphs (due to memory crash for high-dimension SVD \(n>10^5\)), we just use Inc-SVD on DBLP and CitH.
Figure 7 depicts the results when edges are added to DBLP, CitH, YouTu, respectively. For each dataset, we fix |V| and increase |E| by \(|\Delta E|\), as shown in the x-axis. Here, the edge updates are the differences between snapshots w.r.t. the “year” (resp. “video age”) attribute of DBLP, CitH (resp. YouTu), reflecting their real-world evolution. We observe the following. (1) Inc-SR always outperforms Inc-SVD and Inc-uSR when edges are increased. For example, on DBLP, when the edge changes are 10.7%, the time for Inc-SR (83.7s) is 11.2x faster than Inc-SVD (937.4s), and 4.2x faster than Inc-uSR (348.7s). This is because Inc-SR employs a rank-one matrix method to update the similarities, with an effective pruning strategy to skip unnecessary recomputations, as opposed to Inc-SVD that entails rather expensive costs to incrementally update the SVD. The results on CitH are more pronounced, e.g., Inc-SR is 30x better than Inc-SVD when |E| is increased to 401K. (2) Inc-SR is consistently better than Batch when the edge changes are fewer than 19.7% on DBLP, and 7.2% on CitH. When link updates are 5.3% on DBLP (resp. 3.9% on CitH), Inc-SR improves Batch by 10.2x (resp. 4.9x). This is because (i) Inc-SR can exploit the sparse structure of \({\varvec{\Delta }}{} \mathbf{S}\) for incremental update, and (ii) small link perturbations may keep \({\varvec{\Delta }}{} \mathbf{S}\) sparsity. Hence, Inc-SR is highly efficient when link updates are small. (3) The computational time of Inc-SR, Inc-uSR, Inc-SVD, unlike Batch, is sensitive to the edge updates \(|\Delta E|\). The reason is that Batch needs to reassess all similarities from scratch in response to link updates, whereas Inc-SR and Inc-uSR can reuse the old information in SimRank for incremental updates. In addition, Inc-SVD is too sensitive to \(|\Delta E|\), as it entails expensive tensor products to compute SimRank from the updated SVD matrices.
Figure 8 shows the target rank r required for the Li et al.’s lossless SVD approach w.r.t. the edge changes \(|\Delta E|\) on DBLP and CitH. The y-axis is \(\frac{r}{n} \times 100\%\). On each dataset, when increasing \(|\Delta E|\) from 6K to 18K, we see that \(\frac{r}{n}\) is 95% on DBLP (resp. 80% on CitH), Thus, r is not negligibly smaller than n in real graphs. Due to the quartic time w.r.t. r, Inc-SVD may be slow in practice to get a high accuracy.
On synthetic data, we fix \(|V|=79{,}483\) and vary |E| from 485K to 560K (resp. 560K to 485K) in 15K increments (resp. decrements). The results are shown in Fig. 9. We can see that, when 6.4% edges are increased, Inc-SR runs 8.4x faster than Inc-SVD, 4.7x faster than Batch, and 2.7x faster than Inc-uSR. When 8.8% edges are deleted, Inc-SR outperforms Inc-SVD by 10.4x, Batch by 5.5x, and Inc-uSR by 2.9x. This justifies our complexity analysis of Inc-SR and Inc-uSR.
8.2.2 Effectiveness of pruning
Figure 10 shows the pruning power of Inc-SR as compared with Inc-uSR on DBLP, CitH, and YouTu, in which the percentage of the pruned node pairs of each graph is depicted on the black bar. The y-axis is in a log scale. It can be discerned that, on every dataset, Inc-SR constantly outperforms Inc-uSR by nearly 0.5 order of magnitude. For instance, the running time of Inc-SR (64.9s) improves that of Inc-uSR (314.2s) by 4.8x on CitH, with approximately 82.1% node pairs being pruned. That is, our pruning strategy is powerful to discard unnecessary node pairs on graphs with different link distributions.
Since our pruning strategy hinges mainly on the size of the “affected areas” of the SimRank update matrix, Fig. 11 illustrates the percentage of the “affected areas” of SimRank scores w.r.t. link updates \(|\Delta E|\) on DBLP, CitH, and YouTu. We find the following. (1) When \(|\Delta E|\) is varied from 6K to 18K on every real dataset, the “affected areas” of SimRank scores are fairly small. For instance, when \(|\Delta E|=12\)K, the percentage of the “affected areas” is only 23.9% on DBLP, 27.5% on CitH, and 24.8% on YouTu, respectively. This highlights the effectiveness of our pruning method in real applications, where a larger number of elements of the SimRank update matrix with zero scores can be discarded. (2) For each dataset, the size of the “affect areas” mildly grows when \(|\Delta E|\) is increased. For example, on YouTu, the percentage of \(|{\textsf {AFF}}|\) increases from 19.0 to 24.8% when \(|\Delta E|\) is changed from 6K to 12K. This agrees with our time efficiency analysis, where the speedup of Inc-SR is more obvious for smaller \(|\Delta E|\).
8.2.3 Time efficiency of Inc-SR-All and Inc-bSR
We next compare the computational time of Inc-SR-All with Inc-SVD and Batch on DBLP, CitH, and YouTu. For each dataset, we increase |E| by \(|\Delta E|\) that might accompany new node insertions. Note that Inc-SR cannot deal with such incremental updates as \({\varvec{\Delta }}{} \mathbf{S}\) does not make any sense in such situations. To enable Inc-SVD to handle new node insertions, we view new inserted nodes as singleton nodes in the old graph G. Figure 12 depicts the results. We can discern that (1) on every dataset, Inc-SR-All runs substantially faster than Inc-SVD and Batch when \(|\Delta E|\) is small. For example, as \(|\Delta E|=6K\) on CitH, Inc-SR-All (186s) is 30.6x faster than Inc-SVD (5692s) and 15.1x faster than Batch (2809s). The reason is that Inc-SR-All can integrate the merits of Inc-SR with Inc-uSR-C1, Inc-uSR-C2, Inc-uSR-C3 to dynamically update SimRank scores in a rank-one style with no need to do costly matrix–matrix multiplications. Moreover, the complete framework of Inc-SR-All allows itself to support link updates that enables new node insertions. (2) When \(|\Delta E|\) grows larger on each dataset, the time of Inc-SVD increases significantly faster than Inc-SR-All. This larger increase is due to the SVD tensor products used by Inc-SVD. In contrast, Inc-SR-All can effectively reuse the old SimRank scores to compute changes even if such changes may accompany new node insertions.
Figure 13 compares the computational time of Inc-bSR with Inc-SR-All. From the results, we can notice that, on each graph, Inc-bSR is consistently faster than Inc-SR-All. The last column “(%)” denotes the percentage of Inc-bSR improvement on speedup. On each dataset, the speedup of Inc-bSR is more apparent when \(|\Delta E|\) grows larger. For example, on DBLP, the improvement of Inc-bSR over Inc-SR-All is 8.8% when \(|E|=75\)K, and 14.0% when \(|E|=83\)K. On CitH (resp. YouTu), the highest speedup of Inc-bSR over Inc-SR-All is 20.7% for \(|E|=419\)K (resp. 16.4% for \(|E|=901\)K). This is because the large size of \(|\Delta E|\) may increase the number of the new inserted edges with one endpoint overlapped. Hence, more edges can be handled simultaneously by Inc-bSR, highlighting its high efficiency over Inc-SR-All.
8.2.4 Total memory usage
Figure 14 evaluates the total memory usage of Inc-SR-All and Inc-bSR against Inc-SVD on real datasets. Note that the total memory usage includes the storage of the old SimRanks required for all-pairs dynamical evaluation. For Inc-SR-All, we test its three versions: (a) We first switch off our methods of “pruning” and “column-wise partitioning,” denoted as “No Optimization”; (b) next turn on “pruning” only; and (c) finally turn on both. For Inc-SVD, we also tune the default target rank \(r=5\) larger to see how the memory space is affected by r.
The results indicate that (1) on each dataset when the memory of Inc-SVD and Inc-bSR does not explode, the total spaces of Inc-SR-All and Inc-bSR are consistently much smaller Inc-SVD whatever target rank r is. This is because, unlike Inc-SVD, Inc-SR-All and Inc-bSR need not memorize the results of SVD tensor products. (2) When the “pruning” switch is open, the space of Inc-SR-All can be reduced by \(\sim 4\)x further on real data, due to our pruning method that discards many zeros in auxiliary vectors and final SimRanks. (3) When the “column-wise partitioning” switch is open, the space of Inc-SR-All can be saved by \(\sim 100\)x further. The reason is that, as all pairs of SimRanks can be computed in a column-by-column style, there is no need to memorize the entire old SimRank \(\mathbf {S}\) and auxiliary \(\mathbf {M}\). This improvement agrees with our space analysis in Sect. 7. (4) The space of Inc-bSR is 8-11x larger than Inc-SR-All, but is still acceptable. This is because batch updates require more space to memorize several columns from the old \(\mathbf {S}\) to handle a subset of edge updates simultaneously. (5) For Inc-SVD, when the target rank r is varied from 5 to 25, its total space increases from 1.36G to 3.86G on DBLP, but crashes on CitH and YouTu. This implies that r has a huge impact on the space of Inc-SVD, and is not negligible in the big-O analysis of [13].
8.2.5 Exactness
We next evaluate the exactness of Inc-SR-All, Inc-bSR, and Inc-SVD on real datasets. We leverage the NDCG metrics [13] to assess the top-100 most similar pairs. We adopt the results of the batch algorithm [6] on each dataset as the \(\text {NDCG}_{100}\) baselines, due to its exactness. For Inc-SR-All, we evaluate its two enhanced versions: “with column-wise partitioning” and “with pruning”; for Inc-SVD, we tune its target rank r from 5 to 25.
Figure 15 depicts the results, showing the following. (1) On each dataset, the \(\text {NDCG}_{100}\)s of Inc-SR-All and Inc-bSR are 1, which are better than Inc-SVD (\(<0.62\)). This agrees with our observation that Inc-SVD may loss eigen-information in real graphs. In contrast, Inc-SR-All and Inc-bSR guarantee the exactness. (2) The \(\text {NDCG}_{100}\)s for the two versions of Inc-SR-All are exactly the same, implying that both our pruning and column-wise partitioning methods are lossless while achieving high speedup.
8.2.6 Scalability on large graphs
To evaluate the scalability of our incremental techniques, we run Inc-SR-All-P, a memory-efficient version of Inc-SR, on six real graphs (WebB, WebG, CitP, SocL, UK05, and IT04), and compare its performance with LTSF. Both Inc-SR-All-P and LTSF can compute any single column, \(\mathbf {S}_{\star , u}\), of \(\mathbf {S}\) with no need to memorize all \(n^2\) pairs of the old \(\mathbf {S}\). To choose the query node u, we randomly pick up 10,000 queries from each medium-sized graph (WebB and WebG), and 1000 queries from each large-sized graph (CitP, SocL, UK05, and IT04). To ensure every selected u can cover a board range of any possible queries, for each dataset, we first sort all nodes in V in descending order based on their importance that is measured by PageRank (PR), and then split all nodes into 10 buckets: nodes with \(\text {PR} \in [0.9, 1]\) are in the first bucket; nodes with \(\text {PR} \in [0.8, 0.9)\) the second, etc. For every medium- (resp. large-) sized graph, we randomly select 1000 (resp. 100) queries from each bucket, such that u contains a wide range of various types of queries. To generate dynamical updates, we follow the settings in [20], randomly choosing 1000 edges, and considering 80% of them as insertions and 20% deletions.
Figure 16 compares the average time of Inc-SR-All-P and LTSF required to compute any column \(\mathbf {S}_{\star , u}\) w.r.t. a given query u for each edge update on six real graphs. It can be discerned that, on each dataset, Inc-SR-All-P is scalable well over large graphs, and runs consistently 4–7x faster than log-based LTSF per edge update. On one-billion-edge graphs (IT04), for every edge update, the updating time of Inc-SR-All-P (69.301s) is 7.3x faster than that of LTSF (505.794 s). This is because the time of LTSF is dominated by its cost of merging \(R_g=100\) one-way graphs’ log buffers for updating the index. For example, on large IT04, almost 99.92% time required by LTSF is due to its merge operations. In comparison, our memory-efficient method for Inc-SR-All-P takes advantage of the rank-one Sylvester equation which computes the updates to \(\mathbf {S}_{\star , u}\) in a column-by-column style on demand, without the need to merge one-way graphs and memorize all pairs of old \(\mathbf {S}\) in advance.
Figure 17 shows the time complexities of Inc-SR-All-P for four cases of edge insertions on each real dataset. For every graph, we randomly select 1000 edges \(\{(i,j)\}\) for insertion updates, with nodes i and j, respectively, having the probability 1 / 2 to be picked up from the old vertex set V. Hence, each case of edge insertion occurs at 1 / 4 probability. For each insertion case, we sum all the time spent in this case, and divide it by the total number of edge insertions counted for this case. Figure 17 reports the average time per edge update for each case, together with the preprocessing time over each dataset (including the cost of loading the graph and preparing its transition matrix \(\mathbf {Q}\)). From the results, we see that, on each dataset, the time spent for Cases (C0) and (C2) is moderately higher than that for Case (C1); Case (C0) is slightly slower than Case (C2); Case (C3) entails the lowest time cost. These results are consistent with our intuition and mathematical formulation of \({\varvec{\Delta }}{} \mathbf{S}\) for each case. Case (C0) has the most expensive time cost as it needs to iteratively prepare vectors \(\varvec{\xi }_k\) and \(\varvec{\eta }_k\), and old similarities \(\mathbf {S}_{\star ,i}\) and \(\mathbf {S}_{\star ,j}\) via matrix–vector products. In contrast, Case (C2) only requires to iteratively prepare \(\varvec{\xi }_k, \varvec{\eta }_k\) and \(\mathbf {S}_{\star ,i}\); Case (C1) just requires to perform one matrix–vector product to prepare one vector \(\mathbf {y}\). For Case (C3), the new inserted edge forms a new component of the graph. There is no precomputation of any auxiliary vectors, and thus Case (C3) is the fastest.
8.2.7 Precision
To compare the precision of Inc-SR-All-P and LTSF, we define the precision measure [10] for top-k querying:
The original batch algorithm in [9] (resp. [13]) serves as the exact solution to obtain SimRank results for LTSF (resp. Inc-SR-All-P). We evaluate the precision of both algorithms on several real datasets. Figure 18 reports the results on YouTu; the tendencies on other datasets are similar. We see that, when top-k varies from 10 to \(10^5\), the precision of LTSF remains high \((>84\%)\) for small top-k \((<1000)\), but is lower (68–75%) for large top-k \((>{10}^4)\). This is because the probabilistic guarantee for the error bound of LTSF is based on the assumption that no cycle in the given graph has a length shorter than K (the total number of steps). Hence, LTSF is highly efficient for top-k single-source querying, where k is not large. In contrast, the precision of Inc-SR-All-P is stable at 1, meaning that it produces the exact SimRank results of [13], regardless of its top-k size. Thus, Inc-SR-All-P is better for non-top-k query.
8.2.8 Memory of Inc-SR-All-P
Figure 19 evaluates the memory usage of Inc-SR-All-P and LTSF over six real datasets. We observe that both algorithms scale well on large graphs. On WebB, IT04, and UK05, the memory space of Inc-SR-All-P is almost the same as LTSF; On WebG, CitP, and SocL, the memory usage of Inc-SR-All-P is 5–8x less than LTSF. This is because, unlike LTSF that need load a one-way graph to memory, Inc-SR-All-P only requires to prepare the vector information of \(\varvec{\xi }_k, \varvec{\eta }_k\), old \(\mathbf {S}_{\star ,i}\), and old \(\mathbf {S}_{\star ,j}\) to assess the changes to each column of \(\mathbf {S}\) in response to edge update (i, j). The memory space of these auxiliary vectors can sometimes be comparable to the size of the one-way graph and sometimes be much smaller. However, such memory space is linear to n as we do not need \(n^2\) space to store the entire old \(\mathbf {S}\). Note that the old \(\mathbf {S}_{\star ,j}\) and \(\mathbf {S}_{\star ,i}\) can be computed on demand with only linear memory by our partial-pairs SimRank approach [27]. Moreover, we see that, with the growing scale of the real datasets, the memory space of Inc-SR-All-P is increasing linearly, highlighting its scalability on large graphs.
Figure 20 depicts further the average memory usage of Inc-SR-All-P for each case of edge insertion. We randomly pick up 1000 edges \(\{(i,j)\}\) for insertion updates on each dataset, with nodes i and j, respectively, having the probability 1 / 2 to be chosen from the old vertex set V. The average memory space of Inc-SR-All-P for each case is reported in Fig. 20. We see that, on each dataset, the memory required for Cases (C0), (C1), and (C2) are similar, whereas the memory space of Case (C3) is much smaller than the other cases. The reason is that, for Cases (C0), (C1), and (C2), Inc-SR-All-P needs linear memory to store some auxiliary vectors (e.g., \(\varvec{\xi }_k, \varvec{\eta }_k\), \(\mathbf {y}\), old \(\mathbf {S}_{\star ,i}\), and old \(\mathbf {S}_{\star ,j}\)) for updating SimRank scores, whereas for Case (C3), no auxiliary vectors are required for precomputation, thus saving much memory space.
9 Related work
Recent results on SimRank can be distinguished into two categories: (i) dynamical SimRank [8, 10, 13, 20, 25] and (ii) static SimRank [5, 6, 11, 12, 14,15,16, 24].
9.1 Incremental SimRank
Li et al. [13] devised an interesting matrix representation of SimRank, and was the first to show a SVD method for incrementally updating all-pairs SimRanks, which requires \(O(r^4n^2)\) time and \(O({r}^{2}n^2)\) memory. However, their incremental techniques are inherently inexact, with no guaranteed accuracy.
Recently, Shao et al. [20] provided an excellent exposition of a two-stage random sampling framework, TSF, for top-k SimRank dynamic search w.r.t. one query u. In the preprocessing stage, they sampled a collection of one-way graphs to index random walks in a scalable manner. In the query stage, they retrieved similar nodes by pruning unqualified nodes based on the connectivity of one-way graph. To retrieve top- k nodes with highest SimRank scores in a single column \(\mathbf {S}_{\star ,u}\), [20] requires \(O(K^2 R_q R_g)\) average query time to retrieve \(\mathbf {S}_{\star ,u}\) along with \(O(n \log k)\) time to return top-k results from \(\mathbf {S}_{\star ,u}\). The recent work of Jiang et al. [10] has argued that, to retrieve \(\mathbf {S}_{\star ,u}\), the querying time of [20] is \(O(K n R_q R_g)\). The n factor is due to the time to traverse the reversed one-way graph; in the worst case, all n nodes are visited. Moreover, Jiang et al. [10] observed that the probabilistic error guarantee of Shao et al.’s method is based on the assumption that no cycle in the given graph has a length shorter than K, and they proposed READS, a new efficient indexing scheme that improves precision and indexing space for dynamic SimRank search. The query time of READS is O(rn) to retrieve one column \(\mathbf {S}_{\star ,u}\), where r is the number of sets of random walks. Hence, TSF and READS are highly efficient for top- k single-source SimRank search. In comparison, our dynamical method focuses on all \((n^2)\) -pairs SimRank search in \(O(K(m+|{\textsf {AFF}}|))\) time. Optimization methods in this work are based on a rank-one Sylvester matrix equation characterizing changes to \(n^2\) pairs of SimRank scores, which is fundamentally different from [10, 20]’s methods that maintain one-way graphs (or SA forests) updating. It is important to note that, for large-scale graphs, our incremental methods do not need to memorize all \((n^2)\) pairs of old SimRank scores, and can dynamically update \(\mathbf {S}\) column-wisely in only \(O(Kn+m)\) memory. For updating each column of \(\mathbf {S}\), our experiments in Sect. 8 verify that our memory-efficient incremental method is scalable on large real graphs while running 4–7 times faster than the dynamical TSF [20] per edge update, due to the high cost of [20] merging one-way graph’s log buffers for TSF indexing.
There has also been a body of work on incremental computation of other graph-based relevance measures. Banhmani et al. [1] utilized the Monte Carlo method for incrementally computing Personalized PageRank. Desikan et al. [3] proposed an excellent incremental PageRank algorithm for node updating. Their central idea revolves around the first-order Markov chain. Sarma et al. [19] presented an excellent exposition of randomly sampling random walks of short length, and merging them together to estimate PageRank on graph streams.
9.2 Batch SimRank
In comparison to incremental algorithms, the batch SimRank computation has been well-studied on static graphs.
For deterministic methods, Jeh and Widom [9] were the first to propose an iterative paradigm for SimRank, entailing \(O(Kd^2n^2)\) time for K iterations, where d is the average in-degree. Later, Lizorkin et al. [16] utilized the partial sums memorization to speed up SimRank computation to \(O(Kdn^2)\). Yu et al. [24] have also improved SimRank computation to \(O(Kd'n^2)\) time (with \(d' \le d\)) via a fine-grained memorization to share the common parts among different partial sums. Fujiwara et al. [6] exploited the matrix form of [13] to find the top-k similar nodes in O(n) time w.r.t. a given query node. All these methods require \(O(n^2)\) memory to output all pairs of SimRanks. Recently, Kusumoto et al. [11] proposed a linearized method that requires only O(dn) memory and \(O(K^2 d n^2)\) time to compute all pairs of SimRanks. The recent work of [27] proposes an efficient aggregate method for computing partial pairs of SimRank scores. The main ideas of partial-pairs SimRank search are also incorporated into the incremental model of our work, achieving linear memory to update \(n^2\)-pairs similarities.
For parallel SimRank computing, Li et al. [15] proposed a highly parallelizable algorithm, called CloudWalker, for large-scale SimRank search on Spark with ten machines. Their method consists of offline and online phases. For offline processing, an indexing vector is derived by solving a linear system in parallel. For online querying, similarities are computed instantly from the index vector. Throughout, the Monte Carlo method is used to maximally reduce time and space.
The recent work of Zhang et al. [33] conducted extensive experiments and discussed in depth many existing SimRank algorithms in a unified environment using different metrics, encompassing efficiency, effectiveness, robustness, and scalability. The empirical study for 10 algorithms from 2002 to 2015 shows that, despite many recent research efforts, the running time and precision of known algorithms have still much space for improvement. This work makes a further step toward this goal.
Fogaras and Rácz [5] proposed P-SimRank in linear time to estimate a single-pair SimRank s(a, b) from the probability that two random surfers, starting from a and b, will finally meet at a node. Li et al. [14] harnessed the random walks to compute local SimRank for a single node pair. Later, Lee et al. [12] employed the Monte Carlo method to find top-k SimRank node pairs. Tao et al. [22] proposed an excellent two-stage way for the top-k SimRank-based similarity join.
Recently, Tian and Xiao [23] proposed SLING, an efficient index structure for static SimRank computation. SLING requires \(O(n/\epsilon )\) space and \(O(m/\epsilon +n\log \tfrac{n}{\delta } /\epsilon )\) precomputation time and answers any single-pair (resp. single-source) query in \(O(1/\epsilon )\) (resp. \(O(n/\epsilon )\)) time.
10 Conclusions
In this article, we study the problem of incrementally updating SimRank scores on time-varying graphs. Our complete scheme, Inc-SR-All, consists of five ingredients: (1) For edge updates that do not accompany new node insertions, we characterize the SimRank update matrix \({\varvec{\Delta }}{} \mathbf{S}\) via a rank-one Sylvester equation. Based on this, a novel efficient algorithm is devised, which reduces the incremental computation of SimRank from \(O(r^4n^2)\) to \(O(Kn^2)\) for each link update. (2) To eliminate unnecessary SimRank updates further, we also devise an effective pruning strategy that can improve the incremental computation of SimRank to \(O(K(m+|{\textsf {AFF}}|))\), where \(|{\textsf {AFF}}|\ (\ll n^2)\) is the size of the “affected areas” in the SimRank update matrix. (3) For edge updates that accompany new node insertions, we consider three insertion cases, according to which end of the inserted edge is a new node. For each case, we devise an efficient incremental SimRank algorithm that can support new node insertions and accurately update the affected similarities. (4) For batch updates, we also propose efficient batch incremental methods that can handle “similar sink edges” simultaneously and eliminate redundant edge updates. (5) To optimize the memory for all-pairs SimRank updates, we also devise a column-wise memory-efficient technique that significantly reduces the storage from \(O(n^2)\) to \(O(Kn+m)\), without the need to memorize \(n^2\) pairs of SimRank scores. Our experimental evaluations on real and synthetic datasets demonstrate that (a) our incremental scheme is consistently 5–10 times faster than Li et al.’s SVD-based method; (b) our pruning strategy can speed up the incremental SimRank further by 3–6 times; (c) the batch update algorithm enables an extra 5–15% speedup, with just a little compromise in memory; (d) our memory-efficient incremental method is scalable on billion-edge graphs; for every edge update, its computational time can be 4–7 times faster than LTSF and its memory space can be 5–8 times less than LTSF; (e) for different cases of edge updates, Cases (C0) and (C2) entail more time than Case (C1), and Case (C3) runs the fastest.
Notes
\(\Delta G\) consists of a sequence of edges to be inserted/deleted.
According to [13], using our notation, \(r \le \text {rank}({\varvec{\Sigma }} + \mathbf {U}^\mathrm{T} \cdot {\varvec{\Delta }}{} \mathbf{Q} \cdot \mathbf {V})\), where \({\varvec{\Delta }}{} \mathbf{Q}\) is the changes to \(\mathbf {Q}\) for link updates.
In the next sections, we shall substantially reduce its time and memory complexity further.
References
Bahmani, B., Chowdhury, A., Goel, A.: Fast incremental and personalized PageRank. PVLDB 4(3), 173–184 (2010)
Berkhin, P.: Survey: a survey on PageRank computing. Internet Math. 2, 73–120 (2005)
Desikan, P.K., Pathak, N., Srivastava, J., Kumar, V.: Incremental PageRank computation on evolving graphs. In: WWW, pp. 1094–1095 (2005)
Fogaras, D., Rácz, B.: Scaling link-based similarity search. In: WWW, pp. 641–650 (2005)
Fogaras, D., Rácz, B.: Practical algorithms and lower bounds for similarity search in massive graphs. IEEE Trans. Knowl. Data Eng. 19, 585–598 (2007)
Fujiwara, Y., Nakatsuji, M., Shiokawa, H., Onizuka, M.: Efficient search algorithm for SimRank. In: ICDE, pp. 589–600 (2013)
Garg, S., Gupta, T., Carlsson, N., Mahanti, A.: Evolution of an online social aggregation network: an empirical study. In: Internet Measurement Conference, pp. 315–321 (2009)
He, G., Feng, H., Li, C., Chen, H.: Parallel SimRank computation on large graphs with iterative aggregation. In: KDD, pp. 543–552 (2010)
Jeh, G., Widom, J.: SimRank: a measure of structural-context similarity. In: KDD, pp. 538–543 (2002)
Jiang, M., Fu, A.W., Wong, R.C., Wang, K.: READS: a random walk approach for efficient and accurate dynamic SimRank. PVLDB 10(9), 937–948 (2017)
Kusumoto, M., Maehara, T., Kawarabayashi, K.: Scalable similarity search for SimRank. In: SIGMOD, pp. 325–336 (2014)
Lee, P., Lakshmanan, L.V., Yu, J.X.: On top-\(k\) structural similarity search. In: ICDE, pp. 774–785 (2012)
Li, C., Han, J., He, G., Jin, X., Sun, Y., Yu, Y., Wu, T.: Fast computation of SimRank for static and dynamic information networks. In: EDBT, pp. 465–476 (2010)
Li, P., Liu, H., Yu, J.X., He, J., Du, X.: Fast single-pair SimRank computation. In: SDM, pp. 571–582 (2010)
Li, Z., Fang, Y., Liu, Q., Cheng, J., Cheng, R., Lui, J.C.S.: Walking in the cloud: parallel SimRank at scale. PVLDB 9(1), 24–35 (2015)
Lizorkin, D., Velikhov, P., Grinev, M.N., Turdakov, D.: Accuracy estimate and optimization techniques for SimRank computation. PVLDB 1, 422–433 (2008)
Ntoulas, A., Cho, J., Olston, C.: What’s new on the web? The evolution of the web from a search engine perspective. In: WWW, pp. 1–12 (2004)
Rothe, S., Schütze, H.: CoSimRank: A flexible & efficient graph-theoretic similarity measure. In: ACL, pp. 1392–1402 (2014)
Sarma, A.D., Gollapudi, S., Panigrahy, R.: Estimating PageRank on graph streams. J. ACM 58, 13 (2011)
Shao, Y., Cui, B., Chen, L., Liu, M., Xie, X.: An efficient similarity search framework for SimRank over large dynamic graphs. PVLDB 8(8), 838–849 (2015)
Sun, Y., Han, J., Yan, X., Yu, P.S., Wu, T.: PathSim: meta path-based top-\(k\) similarity search in heterogeneous information networks. PVLDB 4, 992–1003 (2011)
Tao, W., Yu, M., Li, G.: Efficient top-\(k\) SimRank-based similarity join. PVLDB 8(3), 317–328 (2014)
Tian, B., Xiao, X.: SLING: a near-optimal index structure for SimRank. In: SIGMOD, pp. 1859–1874 (2016)
Yu, W., Lin, X., Zhang, W.: Towards efficient SimRank computation on large networks. In: ICDE, pp. 601–612 (2013)
Yu, W., Lin, X., Zhang, W.: Fast incremental SimRank on link-evolving graphs. In: ICDE, pp. 304–315 (2014)
Yu, W., McCann, J.A.: Sig-SR: SimRank search over singular graphs. In: SIGIR, pp. 859–862 (2014)
Yu, W., McCann, J.A.: Efficient partial-pairs SimRank search for large networks. PVLDB 8(5), 569–580 (2015)
Yu, W., McCann, J.A.: High quality graph-based similarity retrieval. In: SIGIR, pp. 83–92 (2015)
Yu, W., Lin, X., Zhang, W., McCann, J.A.: Fast all-pairs SimRank assessment on large graphs and bipartite domains. IEEE Trans. Knowl. Data Eng. 27, 1810–1823 (2015)
Yu, W., McCann, J.A.: Gauging correct relative rankings for similarity search. In: CIKM, pp. 1791–1794 (2015)
Yu, W., McCann, J.A.: Random walk with restart over dynamic graphs. In: ICDM, pp. 589–598 (2016)
Yu, W., Lin, X., Zhang, W., McCann, J.A.: Dynamical SimRank search on time-varying networks. Technical report, arXiv:1711.00121 (2017)
Zhang, Z., Shao, Y., Cui, B., Zhang, C.: An experimental evaluation of SimRank-based similarity search algorithms. PVLDB 10(5), 601–612 (2017)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yu, W., Lin, X., Zhang, W. et al. Dynamical SimRank search on time-varying networks. The VLDB Journal 27, 79–104 (2018). https://doi.org/10.1007/s00778-017-0488-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00778-017-0488-z