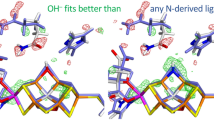
Abstract
Recently, a 1.83 Å crystallographic structure of nitrogenase was suggested to show N2-derived ligands at three sites in the catalytic FeMo cluster, replacing the three \(\mu_{2}\) bridging sulfide ligands (two in one subunit and the third in the other subunit) (Kang et al. in Science 368: 1381–1385, 2020). Naturally, such a structure is sensational, having strong bearings on the reaction mechanism of the enzyme. Therefore, it is highly important to ensure that the interpretation of the structure is correct. Here, we use standard crystallographic refinement and quantum refinement to evaluate the structure. We show that the original crystallographic raw data are strongly anisotropic, with a much lower resolution in certain directions than others. This, together with the questionable use of anisotropic B factors, give atoms an elongated shape, which may look like diatomic atoms. In terms of standard electron-density maps and real-space Z scores, a resting-state structure with no dissociated sulfide ligands fits the raw data better than the interpretation suggested by the crystallographers. The anomalous electron density at 7100 eV is weaker for the putative N2 ligands, but not lower than for several of the \({\mu }_{3}\) bridging sulfide ions and not lower than what can be expected from a statistical analysis of the densities. Therefore, we find no convincing evidence for any N2 binding to the FeMo cluster. Instead, a standard resting state without any dissociated ligands seems to be the most likely interpretation of the structure. Likewise, we find no support that the homocitrate ligand should show monodentate binding.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Nitrogenase is the only enzyme that can catalyse the cleavage of the strong triple bond in N2, thereby making nitrogen available for plants [1]. Nitrogenase reduces N2 to ammonia, through the reaction:
The mechanism is normally discussed in terms of the eight-state Thorneley–Lowe cycle, involving states E0 to E7, differing in the number of added electrons and protons [2, 3]. E0 is the resting state and it is currently believed that N2 binds to E4 with the concomitant release of H2 through reductive elimination of two hydride ions [1].
Several crystal structures have shown that the active site is a complicated MoFe7S9C(homocitrate) cluster [4, 5], the FeMo cluster, shown in Fig. 1. It is essentially composed of two merged Fe4S4 cubane clusters (one with a Mo substitution), connected by three \(\mu_{2}\) bridging sulfide ions and a central carbide ion. The homocitrate ligand binds bidentately to Mo and the cluster is connected to the protein by a histidine ligand to Mo and a single cysteine ligand binding to the terminal Fe ion.
A problem with the mechanistic understanding of nitrogenases has been that it is not clear where the N2 substrate binds – there is no open coordination site or any labile ligands. However, crystal structures of CO-inhibited nitrogenases have shown that CO replaces one of the \(\mu_{2}\) bridging sulfide ions (S2B; atom labels are shown in Fig. 1), bridging Fe2 and Fe6 [6]. A similar replacement was also observed for a crystal structure of a turnover state, which was originally interpreted as showing a N2-derived reaction intermediate [7], but later studies have shown that it probably contains an OH− ion instead [8, 9]. This has inspired computational investigations of reaction mechanisms involving the exchange of S2B with the N2 substrate [10, 11].
Recently, a 1.83 Å crystal structure of nitrogenase was presented, obtained under physiological N2 turnover conditions [12]. The authors suggested that in one of FeMo clusters in the dimeric enzyme, the S2B ligand is replaced by N2, whereas in the other FeMo cluster, the other two \(\mu_{2}\) sulfide ligands (S3A and S5A) are replaced by N2 (or possibly N2H2 or N2H4). The suggestions were supported by anomalous density maps measured at 7100 eV, showing reduced densities for the dissociated sulfide ligands, as well as elongated omit maps, indicating diatomic molecules, rather than the spherical sulfide ions. Based on these findings, the authors suggested that all these three sites are employed in the reaction mechanism (possibly by the rotation of the whole cluster), taking advantage of the differing surroundings that may provide protonation at different positions of the substrate or intermediates.
Of course, such suggestions are sensational and would have a strong impact on the understanding of nitrogenase. Therefore, it is important to ensure that the interpretation of the crystal structure is correct and better than alternative interpretations. In this study, we provide a thorough evaluation of the crystal structure with both standard crystallography means and by quantum refinement [13]. We show that the crystallographic raw data are quite poor, with a strong anisotropy. The arguments for replacement of the three \(\mu_{2}\) sulfide ligands are weak and a model of the E0 resting state with all sulfide ligands bound to the cluster fits the data at least as good as the structure presented in the original publication.
Methods
Crystal structure
This study is based on the 6UG0 crystal structure of Mo nitrogenase at 1.83 Å resolution [12]. Coordinates, occupancies, B factors and structure factors were obtained from the Protein Data Bank, together with the space group, unit-cell parameters, resolution limits, \(R\) factors and the test set used for the evaluation of the Rfree factor. For the evaluation of the deposited structure, the electron-density map coefficients were also downloaded from the Protein Data Bank. The anomalous electron density map was downloaded from Zenodo [14].
Quantum refinement
In standard crystallographic refinement, the current model (coordinates, B factors, occupancies, etc.) is optimised by minimising the difference between structure factors observed experimentally or calculated from the model [15]. Owing to the limited resolution of protein crystal structures, it is normally necessary to introduce restraints in the crystallographic refinement to ensure that the structure makes chemical sense. These restraints are usually derived from high-resolution structures [16] and in the language of computational chemistry, they represent a molecular-mechanics (MM) force field. Therefore, the refinement optimises an energy function of the form
Here, EXray is the crystallographic goodness-of-fit criterion, typically a maximum-likelihood function [17, 18], EMM is the empirical restraints and wA is a weight factor determining the relative importance of the two terms.
The empirical restraints are most accurate for protein residues and nucleic acids, for which there are much accurate experimental data. However, for cofactors, substrates and inhibitors, much less information is available, making the restraints less certain [19]. Even worse, for metal sites, it is hard to set up an empirical potential [20] and it depends strongly on all the ligands, as well as the charge and spin state of the metal. Therefore, these parts of crystal structures have a lower accuracy than the amino-acid parts.
To overcome these problems, the empirical restraints can be replaced by quantum–mechanical (QM) calculations. This can be done for a small, but interesting part of the structure (e.g. the active site) in the same way as in standard QM/MM methods [21, 22]. This part is called system 1 in the following. This leads to the quantum-refinement energy function [13].
Here, EQM1 is the QM energy of system 1. To avoid double-counting of energy terms, we need to subtract the corresponding MM energy of system 1, EMM1. wMM is another weight factor that is necessary because the empirical restraints are normally in statistical units, whereas the QM energy is in energy units.
Such an energy function is implemented in the ComQum-X software [13], which is an interface between the QM software Turbomole [23] and the software crystallography and NMR system (CNS) [24, 25]. We employed the default wA factor, selected by CNS, 1.5368. Likewise, we used wMM = 1/3 as in all our previous applications [13].
QM calculations
The QM calculations were performed at the TPSS/def2-SV(P) level of theory [26, 27]. The calculations were sped up by expanding the Coulomb interactions in an auxiliary basis set, the resolution-of-identity (RI) approximation [28, 29]. Empirical dispersion corrections were included with the DFT-D4 approach [30, 31]. We studied the FeMo clusters in both the A and C subunit of the protein. In both cases, the QM systems were FeMo cluster, homocitrate, the imidazole ring from His-442, the side chain of Cys-275 and the side chains of Arg-96 and Arg-359 (modelled as CH3NHC(NH2)2+). The two Arg residues where included to compensate the negative charge of the cluster. The QM system is shown in Fig. 1.
In the \(E_{0}\) resting state of Mo nitrogenase, the FeMo cluster is in the Mo(III)Fe(II)3Fe(III)4 oxidation state [32, 33]. This gives a net charge of –3 for the QM system in Fig. 1. It is normally assumed that this charge is conserved throughout the Thorneley–Lowe reaction cycle, because each added electron is accompanied by a proton. However, when a sulfide ion dissociates, it takes two negative charges with it (S2−), so that the net charge of the cluster increases by two for each dissociated sulfide. Therefore, we have assumed that structures with one sulfide ion displaced by N2 has a net charge of − 1, whereas models with two N2 molecules have a net charge of + 1. On the other hand, we assumed that systems with N2 and N2H2 have the same net charge (because they represent two different \(E_{n}\) states, viz. after the addition of two electrons and protons). In three cases, we tested also a net charge of − 3 for the N2-bound systems, i.e. assuming that the net charge of the cluster is conserved also after the dissociation of the sulfide ion. That would correspond to a formal reduction of two Fe ions. All structures were studied in the quartet state, which is the observed spin state for \(E_{0}\) [1].
The electronic structure in all QM calculations was obtained with the broken-symmetry approach [34]: each of the seven Fe ions were modelled in the high-spin state, with either a surplus of \(\alpha\) (four Fe ions) or \(\beta\) (three Fe ions) spin. We employed the broken-symmetry BS7-235 state with \(\beta\) spin on Fe2, Fe3 and Fe5 for all calculations (the numbering of the Fe ions is shown in Fig. 1). This is the best broken-symmetry state for the resting state of Mo nitrogenase and also for several other \(E_{n}\) states [34,35,36]. This state was obtained using the fragment approach by Szilagyi and Winslow [37] or by swapping the coordinates of the Fe ions [38].
Result and discussion
We have performed a critical evaluation of the recent crystal structure of nitrogenase (6UG0 at 1.83 Å resolution) [12], suggested to show that in chain A, one of the \(\mu_{2}\) bridging belt sulfide ions of the FeMo cluster (S2B) is replaced by a N2 ligand (possibly protonated), whereas in chain C, instead the other two \(\mu_{2}\) bridging sulfide ions (S3A and S5A) are replaced by N2. We employ standard crystallographic metrics (electron-density maps and RSZD scores), as well as quantum refinement to evaluate the structure and study whether there are any convincing arguments that the sulfide ions really are replaced by N2. In the following we will call the three sites 2B, 3A and 5A, corresponding to the binding sites of S2B, S3A and S5A, respectively (Fig. 1), even when N2 is binding in that site.
The original crystal structure
We start by describing the deposited structure and the corresponding electron-density maps (downloaded from the PDB server, https://www.rcsb.org/structure/6UG0). The 2mFo–DFc electron-density map of the FeMo cluster in chain A is shown in Fig. 2a. The Fe ion peaks start to be visible in the 2mFo–DFc map at 15.4 \(\sigma\), but the weakest one (Fe) appears at 10.9 \(\sigma\). The S ion peaks start appearing at 8.4 \(\sigma\) while the putative N2 ligand is a \(\sim\) 6.8 \(\sigma\) peak. On the other hand, S1A in the same cluster is only a 5.7 \(\sigma\) peak and the Cys sulfur a 5.3 \(\sigma\) peak, so the 2B site does not have the lowest electron density among the S ions in the cluster. In fact, the 2mFo–DFc electron-density map shows a conspicuous layered structure and sites outside these layers seem to have a lower electron density.
To obtain more robust measures of the density peak volumes, we have integrated the 2mFo–DFc electron density around each S atom in the crystal structure within a sphere with a radius of 1.05 Å (the covalent radius of S). The results are shown in Table 1. It can directly be seen that the integrated density at the 2B site is not particularly low, neither when compared to all other S atoms in the crystal structure (+ 0.6 \(\sigma\), i.e. larger than the average) nor when compared to all the other S atoms in the cluster (close to the average value).
The layered structure becomes even clearer when considering the mFo–DFc electron-density difference maps (Fig. 2b), showing alternating layers of positive and negative densities. In particular, there is strong positive densities at almost all atoms in the FeMo cluster and strong negative density between the atoms. The positive density is highest close to the central carbide ion (6.7 \(\sigma\)), but it is high also close to the N2 ligand (6.6 \(\sigma\)), indicating that the N2 model contains too few electrons (N2 contains 14 electrons, whereas S2– contains 18 electrons). The largest positive density at any other S atom of the FeMo cluster appears at \(\sim\) 5.6 \(\sigma\) (but there is a layer of positive density between Fe7 and S5A at 6.1 \(\sigma\).
In chain C, the crystal structure suggests that S2B is present, but both S3A and S5A are replaced by N2 (again possibly protonated). Figure 3a shows the 2mFo–DFc electron density of the FeMo cluster in chain C. The Fe ion peaks start to appear at 15.5 \(\sigma\) and all are visible at 13.6 \(\sigma\). The sulfide ions start to appear at 9.7 \(\sigma\) (S2A). There is electron density at the N2 ligand in the 5A site already at 9.3 \(\sigma\), when several sulfide ions are still not seen, including S2B. Density is seen at the other N2 ligand at 8.6 \(\sigma\) and at the same level also S2B starts to appear. S4B does not appear until 7.5 \(\sigma\). The integrated densities show that the 3A and 5A sites actually have high densities compared to all S atoms (1.3–1.4 \(\sigma\)), but slightly lower than for the \(\mu_{3}\) bridging sulfide ions (–0.3 \(\sigma\) compared to all S atoms in the cluster), but the deviation is very small (the S2B ion actually has a much smaller integrated density). Thus, there is no indication from the electron density that S3A and S5A have been replaced by other ligands.
The mFo–DFc electron-density difference maps of the FeMo cluster in chain C are shown in Fig. 3b. They also show a layered structure and large difference densities in the FeMo cluster. The largest positive density is found between Mo and the OH group of the homocitrate ligand (8.9 \(\sigma\)), but there are also large positive densities both at the N2 ligand in the 3A site and between Fe7 and S3B (\(\sim\) 8.0 \(\sigma\)). A positive density appears at the other N2 ligand at 7.7 \(\sigma\). None of the other S ligands have any positive density until \(\sim\) 3 \(\sigma\).
The prominent layer-like features of the electron density can be linked to a strong anisotropy of the data. In fact, the data extends to the reported 1.83 Å resolution along the c*-axis, but along the b*-axis the resolution is only \(\sim\) 2.6 Å according to the PDBPeep server [39]. Since \(I{/}\sigma \left( I \right) > 5\) in the best direction at the 1.83 Å resolution cutoff, it cannot be excluded that the layers are anisotropic Fourier ripples around the electron rich FeMo cluster. There are also missing wedges of data around the a* and c* axes, which further degrades the quality of the data set.
Interestingly, the original authors selected to refine the structure with anisotropic B factors, although the resolution is only 1.83 Å. This is strongly questionable, especially given the anisotropy of the data. Even with isotropic data to 1.83 Å, the use of anisotropic B factors would hardly be standard, but the marked data anisotropy causes an unphysical systematic effect in the B factors. Figure S2 in the supplementary material indeed shows that all B factors are strongly anisotropic, in contrast to normal high-resolution structures, in which most atoms have almost spherical B factors. The anisotropy follows the layers in the difference density, implying that the two phenomena are connected. Naturally, this will strongly affect the interpretation of the structure, in particular whether the replaced sulfide ligands are interpreted as a single atom or two N atoms. In that regard, it is important to note that the two N atoms of the N2 ligands always lie along the axis of maximum anisotropy. This indicates that the interpretation of the ligands as diatomic ligand may actually be an artefact of the anisotropy of the data.
To avoid this bias, we refined the structure with only isotropic B factors in the following sections, using default settings with the Phenix software.
Quantum refinement
Next, we used the method of quantum refinement to test different models of the crystallographic data, viz. testing either S2–, N2 or N2H2 in the 2B (chain A) or 3A and 5A (chain C) binding sites. Quantum refinement is standard crystallographic refinement in which the empirical restraints are replaced by accurate QM calculations for a small (but interesting) part of the structure. Thereby, we introduce information of the expected structure with different sets of ligands, which may help the interpretation of the structure. We judge the results in terms of the real-space Z score (RSZD) for the various parts of the QM system (other atoms are kept at the original crystal structure) and the mFo–DFc electron-density difference maps (obtained using Phenix without any anisotropic B factors).
The RSZD scores for chain A are shown in Table 2. It can be seen that a S2– ligand gives slightly smaller RSZD scores than a N2 ligand. In particular, the RSZD score around the 2B site is 2.1 for S2– but 2.7 for N2. Moreover, the sum of the RSZD scores of all atoms in the QM system are 21.8 for S2–, but 23.0 for N2. Changing the net charge of the QM system for the N2-bound model to − 3 (i.e. the same as for the S2–-bound model instead of − 1, has only a small effect on the RSZD scores, but gives slightly worse results (the sum of the RSZD scores increases to 23.7).
This interpretation is also confirmed by the mFo–DFc electron-density difference maps for the FeMo cluster in chain A with the 2B site modelled either with S2− or N2, shown in Fig. 4. It can be seen that the N2 ligand gives rise to a large positive density around the ligand, indicating that it contains too few electrons. On the other hand, the S2− ligand does not show any negative density, although there are some enhanced negative densities around the Fe6 ion and in the direction towards S2B.
For chain C, we performed six different quantum-refinement calculations employing different ligands in the 3A and 5A binding sites, viz. either S2−, N2 or N2H2. The results in Table 3 show that the model with S2– in both sites clearly gives the best results. In particular, the sum of the RSZD scores of the QM system is 16.3, whereas the other five models have sums of 18.2–23.3, with the structure using N2 in both sites (i.e. the interpretation in the original crystal structure) giving the worst results. Likewise, it can be seen that all models with S2– in site 5A give an appreciably lower RSZD score for site 5A (1.1–1.4), than N2 (3.2–3.7), and that N2H2 gives the worst results (5.7). The results are similar (but slightly worse) in site 3A: all models with S2– give lower RSZD (2.8–3.1) than N2 (5.1–6.3) or N2H2(6.7).
This is also supported by the mFo–DFc electron-density difference maps in Fig. 5, showing that the model with two N2 ligands give significant positive densities for the two N2 ligands, indicating that they contain too few electrons. On the other hand, if we instead use two S2– ligands, no negative difference densities are seen around the ligands in the 3A and 5A sites, which would indicate that they contain too many electrons (there is instead still some positive density around the S3A ion). mFo–DFc difference maps for the other quantum-refined structures are given in the supplementary material.
Thus, the quantum-refinement calculations give no support to the suggestion that some of the \(\mu_{2}\) sulfide ligands are replaced by N2 in any of the two chains. On the contrary, a normal cluster with all sulfide ligands remaining gives appreciably better results.
Anomalous densities
The strongest argument for the replacement of the \(\mu_{2}\) belt sulfide ions came from an analysis of the anomalous densities [12]. Electron-density maps collected at 7100 eV show signals that mainly reflect sulfur and molybdenum atoms. Figure 6 shows the 2mFo–DFc anomalous maps for the two FeMo clusters (2.18 Å resolution) [12]. It can be seen that there are significant anomalous densities at all sulfur sites in the two clusters (3.3–8.3 \(\sigma\)), including the \(\mu_{2}\) bridging sites. However, the density is somewhat lower at the sites modelled by N2 (in the original publication [12], the maps were shown at a \(\sigma\)-level just before densities are seen at the sites modelled as N2). On the other hand, the very large anomalous density on the Mo ion does not reach the three coordinated sulfide ions (S1B, S3B and S4B) until a level at which the anomalous density at the putative N2 sites is large. In particular, the anomalous densities at the putative N2 sites are appreciably higher than the noise level (the first peaks at random positions appear at 3.1 \(\sigma\)).
Anomalous-density 2mFo–DFc maps around the active-side MoFe cluster (left: chain A at 3.3 σ and right: chain C at 4.4 σ) of Mo nitrogenase. In the upper figures, S2B points to the left, S3A points up and S5A points down. The two lower figures show a transverse view, like the one in Fig. 1
It is also notable that the anomalous densities are significantly larger for the FeMo cluster in chain C than for the cluster in chain A (by 1.4 \(\sigma\) units on average). This difference is connected to appreciably higher B factors for all atoms in the FeMo cluster in chain A (average 47) than in chain B (average 34).
As for the electron density, we obtain more reliable estimates by integrating the anomalous 2mFo–DFc electron densities within a sphere with the covalent radius of S. The results are collected in Table 4. It can be seen that the integrated anomalous density at the 3A and 5A sites of chain C (8.6 and 8.8 \(e\)) indeed is lower than in the S2B site (11.9 \(e\)) and the Fe-side sulfur atoms (S1A, S2A and S4A, 9.7–13.0 \(e\)). However, the integrated anomalous densities of two of the Mo-side sulfide ions (S3B and S4B) are similar or even lower, 8.2–8.8 \(\sigma\). If the integrated anomalous densities are compared to those of all other S atoms in the crystal structure, the densities at the 3A and 5A sites are just below the average (− 0.2 and − 0.1 \(\sigma\)). If they are instead compared to the other eight S atoms in the C-chain FeMo cluster, the deviation is somewhat larger (− 0.9 and − 0.8 \(\sigma\)), but these deviations are far from significant.
Likewise, it can be seen that the integrated anomalous density at the 2B site in chain A (6.0 \(e\)) is lower than in the 3A and 5A sites (8.4–9.0 \(e\)) and actually lower than for any of the sulfur atoms in the cluster (7.3–12.0 \(e\)). Compared to all the (140) other S atoms in the crystal structure, it is rather small (− 1.3 \(\sigma\)), but there are 16 atoms with lower integrated anomalous densities (11%). Compared to the other nine S atoms in the same FeMo cluster, it deviates by − 1.7 \(\sigma\), corresponding to a significance of 0.87. Thus, it is not unexpected that one of ten sulfur atoms shows a deviation of that level (the Cys sulfur atom of the same cluster shows the same deviation in the opposite direction).
Thus, we conclude that not even the anomalous densities give any strong support to the suggestion that the sulfur ions are replaced by N2-derived ligands. In particular, there is no doubt that all sites are significantly occupied with sulfur ions (cf. Figure 6).
Distances to the homocitrate ligand
In the original publication [12], the authors reported large differences in the Mo–O distances to the homocitrate ligand in the two FeMo clusters. In chain A, the Mo–O distance to the alcohol group on homocitrate (O7) is 2.35 Å, whereas the distance to the carboxylate oxygen (O6) is 2.73 Å. Both distances are appreciably longer than in accurate crystal structures of the resting state of the FeMo cluster, e.g. 2.18 and 2.21 Å, respectively, in the 3U7Q structure [4]. In the FeMo cluster in chain C, the distances are similar, but opposite: the distance to the alcohol group is long, 2.74 Å, whereas the distance to the carboxylate group is 2.32 Å (according to the 6UG0 structure; the article reports a distance of 2.0 Å [12]). The authors suggested that these differences may be mechanistically significant, possibly representing protonation events of the hydroxyl group [12].
Interestingly, our quantum-refinement calculations give no support to this suggestion as can be seen in Table 5. All calculations give nearly the same Mo–O distances for the hydroxyl and carboxylate groups (within 0.03 Å). Moreover, they are short in all structures, 2.05–2.16 Å. They are shortest with two N2 ligands (2.05–2.06 Å), intermediate with one N2 group (2.08–2.12 Å) and longest with only sulfide ligands (2.10–2.16 Å), reflecting the net charge of the cluster. This is confirmed by the N2 calculations with a net QM charge of − 3, which give 0.01–0.04 Å longer Mo–O bonds than the corresponding calculations with a net charge of − 1.
For the FeMo cluster in chain C, the electron-density difference maps in Fig. 5 show no significant features around the Mo ion and the homocitrate ligand. In particular, the structure is strongly improved compared to the original crystal structures, shown in Fig. 3. This is also reflected in the RSZD scores in Table 3. This indicates that the original crystal structure contains distances that are wrong by \(\sim\) 0.6 Å. For the FeMo cluster in chain A, the situation is slightly less clear, because the quantum-refined structures show strong negative densities around the Mo ion (cf. Figure 4). However, the structure is still appreciably better than the original crystal structure in Fig. 2, as is confirmed by the RSZD scores in Table 2.
Finally, we note that the quantum-refined structures with no N2 ligands reproduce the metal–metal and metal–ligand distances in the high-resolution crystal structure of the resting state [4] within 0.03–0.08 Å with maximum deviations of 0.08–0.20 Å. Thus, there are no indications of any significant changes in the structure compared to the resting state.
Conclusions
In this study, we have made a critical evaluation of the recent crystal structure of Mo nitrogenase [12], suggested to show that the \(\mu_{2}\) bridging sulfide ligands are replaced by substrate N2-derived ligands. We make several important observations.
-
The crystal structure is of poor and uneven quality, with a strong anisotropy.
-
The electron-density maps (Figs. 2 and 3) do not give any support for the binding of N2 to the cluster and there is no indication that the electron density for the putative N2 ligands is significantly lower than for the other sulfide sites. On the contrary, the suggested N2 ligands give rise to strong and highly significant positive difference densities in both clusters (Figs. 2b and 3b).
-
The suggestion that the \(\mu_{2}\) bridging ligands are diatomic is probably an artefact caused by the strong anisotropy of the data.
-
Quantum-refinement calculations with different interpretations of the atoms in the \(\mu_{2}\) positions (Tables 2 and 3) show that sulfide ligands always give better RSZD scores than N2 or N2H2 ligands. This is also supported by difference electron-density maps (Figs. 4 and 5).
-
Likewise, the quantum-refinement calculations give no support to the suggestion that the homocitrate ligand should bind monodentately in the crystal structure.
-
Anomalous electron-density maps, obtained at 7100 eV (Fig. 6), show that the anomalous density indeed is somewhat lower at the putative N2 sites, but it is still significant and actually larger than for the sulfides on the Mo-side of the cluster. Moreover, a statistical analysis of the anomalous densities (Table 4), show that the densities are not lower than what could be expected by random variations.
Consequently, we conclude that there is no convincing evidence that the crystal structure should show any bound N2-derived ligands. Instead, a standard resting state with nine sulfide ligands seems to be a better interpretation.
References
Hoffman BM, Lukoyanov D, Yang Z-Y et al (2014) Mechanism of nitrogen fixation by nitrogenase: the next stage. Chem Rev 114:4041–4062. https://doi.org/10.1021/cr400641x
Thorneley RNF, Lowe DJ (1984) The mechanism of Klebsiella pneumoniae nitrogenase action. Pre-steady-state kinetics of an enzyme-bound intermediate in N2 reduction and of NH3 formation. Biochem J 224:887–894. https://doi.org/10.1042/bj2240887
Thorneley RNF, Lowe DJ (1985) Kinetics and mechanism of the nitrogenase enzyme system. In: Spiro TG (ed) Molybdenum enzymes. Wiley, New York, pp 221–284
Spatzal T, Aksoyoglu M, Zhang L et al (2011) Evidence for Interstitial Carbon in Nitrogenase FeMo cofactor. Science (80-) 120:940. https://doi.org/10.1126/science.1214025
Einsle O, Rees DC (2020) Structural enzymology of nitrogenase enzymes. Chem Rev 120:4969–5004. https://doi.org/10.1021/acs.chemrev.0c00067
Spatzal T, Perez KA, Einsle O et al (2014) Ligand binding to the FeMo-cofactor: Structures of CO-bound and reactivated nitrogenase. Science 345:1620–1623. https://doi.org/10.1126/science.1256679
Sippel D, Einsle O (2017) The structure of vanadium nitrogenase reveals an unusual bridging ligand. Nat Chem Biol 13:956–960. https://doi.org/10.1038/nchembio.2428
Benediktsson B, Thorhallsson AT, Bjornsson R (2018) QM/MM calculations reveal a bridging hydroxo group in a vanadium nitrogenase crystal structure. Chem Commun 54:7310–7313. https://doi.org/10.1039/C8CC03793K
Cao L, Caldararu O, Ryde U (2020) Does the crystal structure of vanadium nitrogenase contain a reaction intermediate? Evidence from quantum refinement. J Biol Inorg Chem 25:847–861. https://doi.org/10.1007/s00775-020-01813-z
Varley JB, Wang Y, Chan K et al (2015) Mechanistic insights into nitrogen fixation by nitrogenase enzymes. Phys Chem Chem Phys 17:29541–29547. https://doi.org/10.1039/C5CP04034E
Cao L, Ryde U (2020) Putative reaction mechanism of nitrogenase after dissociation of a sulfide ligand. J Catal 391:247–259. https://doi.org/10.1016/j.jcat.2020.08.028
Kang W, Lee CC, Jasniewski AJ et al (2020) Structural evidence for a dynamic metallocofactor during N2 reduction by Mo-nitrogenase. Science (80-) 368:1381–1385. https://doi.org/10.1126/science.aaz6748
Ryde U, Olsen L, Nilsson K (2002) Quantum chemical geometry optimizations in proteins using crystallographic raw data. J Comput Chem 23:1058–1070. https://doi.org/10.1002/jcc.10093
Kang W, Lee CC, Jasniewski AJ et al (2020) Anomalous datasets for 6UG0 and 6VXT. Zenodo. https://doi.org/10.5281/zenodo.3756201
Kleywegt GJ, Jones TA (1997) Model building and refinement practice. Meth Enzym 227:208–230
Engh RA, Huber R (1991) Accurate bond and angle parameters for X-ray protein structure refinement. Acta Crystallogr Sect A 47:392–400. https://doi.org/10.1107/S0108767391001071
Pannu NS, Read RJ (1996) Improved structure refinement through maximum likelihood. Acta Crystallogr Sect A A52:659–668. https://doi.org/10.1107/S0108767396004370
Adams PD, Pannu NS, Read RJ, Brünger AT (1997) Cross-validated maximum likelihood enhances crystallographic simulated annealing refinement. Proc Natl Acad Sci USA 94:5018–5023. https://doi.org/10.1073/pnas.94.10.5018
Kleywegt GJ (2007) Crystallographic refinement of ligand complexes. Acta Crystallogr Sect D 63:94–100. https://doi.org/10.1107/S0907444906022657
Hu L, Ryde U (2011) Comparison of methods to obtain force-field parameters for metal sites. J Chem Theory Comput 7:2452–2463. https://doi.org/10.1021/ct100725a
Senn HM, Thiel W (2009) QM/MM methods for biomolecular systems. Angew Chem Int Ed 48:1198–1229. https://doi.org/10.1002/anie.200802019
Ryde U (2016) QM/MM calculations on proteins. Methods Enzymol 577:119–158. https://doi.org/10.1016/bs.mie.2016.05.014
Furche F, Ahlrichs R, Hättig C et al (2014) Turbomole. Wiley Interdiscip Rev Comput Mol Sci 4:91–100. https://doi.org/10.1002/wcms.1162
Brunger AT, Adams PD, Clore GM et al (1998) Crystallography & NMR system: a new software suite for macromolecular structure determination. Acta Crystallogr D 54:905–921. https://doi.org/10.1107/S0907444998003254
Brunger AT (2007) Version 1.2 of the Crystallography and NMR system. Nat Protoc 2:2728–2733. https://doi.org/10.1038/nprot.2007.406
Tao J, Perdew JP, Staroverov VN, Scuseria GE (2003) Climbing the density functional ladder: non-empirical meta-generalized gradient approximation designed for molecules and solids. Phys Rev Lett 91:146401. https://doi.org/10.1103/PhysRevLett.91.146401
Weigend F, Ahlrichs R (2005) Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys Chem Chem Phys 7:3297–3305. https://doi.org/10.1039/b508541a
Eichkorn K, Treutler O, Öhm H et al (1995) Auxiliary basis-sets to approximate coulomb potentials. Chem Phys Lett 240:283–289. https://doi.org/10.1016/0009-2614(95)00621-a
Eichkorn K, Weigend F, Treutler O, Ahlrichs R (1997) Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor Chem Acc 97:119–124. https://doi.org/10.1007/s002140050244
Caldeweyher E, Bannwarth C, Grimme S (2017) Extension of the D3 dispersion coefficient model. J Chem Phys 147:34112. https://doi.org/10.1063/1.4993215
Caldeweyher E, Ehlert S, Hansen A et al (2019) A generally applicable atomic-charge dependent London dispersion correction. J Chem Phys 150:154122. https://doi.org/10.1063/1.5090222
Bjornsson R, Lima FA, Spatzal T et al (2014) Identification of a spin-coupled Mo(III) in the nitrogenase iron–molybdenum cofactor. Chem Sci 5:3096–3103. https://doi.org/10.1039/C4SC00337C
Bjornsson R, Neese F, DeBeer S (2017) Revisiting the Mössbauer isomer shifts of the FeMoco cluster of nitrogenase and the cofactor charge. Inorg Chem 56:1470–1477. https://doi.org/10.1021/acs.inorgchem.6b02540
Lovell T, Li J, Liu T et al (2001) FeMo cofactor of nitrogenase: a density functional study of states MN, Mox, MR, and MI. J Am Chem Soc 123:12392–12410. https://doi.org/10.1021/ja011860y
Cao L, Caldararu O, Ryde U (2018) Protonation and reduction of the FeMo cluster in nitrogenase studied by quantum mechanics/molecular mechanics (QM/MM) calculations. J Chem Theory Comput 14:6653–6678. https://doi.org/10.1021/acs.jctc.8b00778
Cao L, Ryde U (2018) Influence of the protein and DFT method on the broken-symmetry and spin states in nitrogenase. Int J Quantum Chem 118:e25627. https://doi.org/10.1002/qua.25627
Szilagyi RK, Winslow MA (2006) On the accuracy of density functional theory for iron—sulfur clusters. J Comput Chem 27:1385–1397. https://doi.org/10.1002/jcc.20449
Greco C, Fantucci P, Ryde U, de Gioia L (2011) Fast generation of broken-symmetry states in a large system including multiple iron–sulfur assemblies: Investigation of QM/MM energies, clusters charges, and spin populations. Int J Quantum Chem 111:3949–3960. https://doi.org/10.1002/qua.22849
Tickle IJ, Sharff A, Flensburg C, et al (2020) The STARANISO/PDBpeep Server. http://staraniso.globalphasing.org/172cgi-bin/PDBpeep.cgi?crit=tism&tval=1.20&ID=6ug0. Accessed 15 Dec 2020
Acknowledgements
This investigation has been supported by grants from the Swedish research council (project 2018-05003) and from eSSENCE: the e-science collaboration. The computations were performed on computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University and HPC2N at Umeå University, partially funded by the Swedish Research Council (grant 2018-05973).
Funding
Open access funding provided by Lund University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bergmann, J., Oksanen, E. & Ryde, U. Critical evaluation of a crystal structure of nitrogenase with bound N2 ligands. J Biol Inorg Chem 26, 341–353 (2021). https://doi.org/10.1007/s00775-021-01858-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00775-021-01858-8