Abstract
Formate dehydrogenases (FDHs) are metalloenzymes that catalyse the reversible conversion of formate to carbon dioxide. Since such a process may be used to combat the greenhouse effect, FDHs have been extensively studied by experimental and theoretical methods. However, the reaction mechanism is still not clear; instead five putative mechanisms have been suggested. In this work, the reaction mechanism of FDH was studied by computational methods. Combined quantum mechanical and molecular mechanic (QM/MM) optimisations were performed to obtain the geometries. To get more accurate energies and obtain a detailed account of the surroundings, big-QM calculations with a very large (1121 atoms) QM region were performed. Our results indicate that the formate substrate does not coordinate directly to Mo when it enters the oxidised active site of the FDH, but instead resides in the second coordination sphere. The sulfido ligand abstracts a hydride ion from the substrate, giving a Mo(IV)–SH state and a thiocarbonate ion attached to Cys196. The latter releases CO2 when the active site is oxidised back to the resting (MoVI) state. This mechanism is supported by recent experimental studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Biological transformations of carbon dioxide (CO2) are key processes in the global carbon cycle and have lately attracted great attention, because they may be used to combat the greenhouse effect [1,2,3,4,5,6,7]. In nature, the reversible conversion of CO2 to formate (HCOO−), shown in Eq. 1, is catalysed by formate dehydrogenases (FDHs) [4, 8,9,10,11]. The product of the reduction reaction, formate, is an ideal hydrogen fuel, with the advantage of being safe and clean [4].
The FDHs are divided into two classes, based on whether they require metal ions for their activity or not: metal independent [12,13,14,15,16,17] and metal dependent [8, 18]. The former class comprises NAD-dependent enzymes that belong to the D-specific dehydrogenases of the 2-oxyacid family and can be widely found in bacteria, yeasts, fungi and plants. The latter class comprises prokaryotic enzymes that harbour one tungsten (W) or molybdenum (Mo) ion in their active sites [4, 8,9,10]. We will focus on the Mo-FDHs in this paper.
The Mo-FDHs are structurally diverse, but the active site is highly conserved [9, 10]. Crystallographic studies have revealed three main classes of Mo-FDHs: one consisting of monomeric cytoplasmic enzymes (FDH H), which contain only the molybdenum centre and one Fe–S cluster [19,20,21,22,23], and two classes of more complex heteromeric (αβγ) membrane-bound respiratory enzymes (FDH N and O), which contain seven [24,25,26,27,28] or six additional redox-active centres (Fe–S clusters and heme groups) [29,30,31], besides the Mo active site. However, the active sites of all Mo-FDHs (Fig. 1) contain in the oxidised (MoVI) state two molybdopterin guanine dinucleotide (MGD) cofactors, one protein-derived ligand (cysteine or selenocysteine) and a sulfido group, which coordinate with Mo ion in a distorted hexa-coordinated trigonal prismatic geometry [22,23,24, 32, 33].
However, for the reduced (MoIV) state, the structure is still not fully clear. Boyingto et al. [22] reported that the Mo ion is penta-coordinate with the two MGD ligands in the equatorial positions and the selenium atom of the selenocysteine (Sec) residue in the axial position, leading to an approximate square pyramidal geometry. However, Raaijmakers and Romão reinterpreted this structure and suggested that the Sec residue has dissociated from Mo and the fifth axial ligand is a sulfido group [23]. X-ray absorption spectroscopy suggests that the Sec/Cys residue is still bound to Mo [33,34,35]. In particular, EXAFS data show a Se–S bond of 2.19 Å between Sec and the sulfido group [34, 35]. In addition, the Sec/Cys residue still binds to the Mo(V) ion according to electron paramagnetic resonance (EPR) spectroscopy [36, 37].
Although FDHs play an important role by oxidising formate and reducing carbon dioxide in nature and have been studied extensively by both experimental and computational methods, the reaction mechanism is still not fully understood [8, 9, 18, 33, 38]. Raaijmakers et al. have suggested a mechanism, based on the crystal structure, which involves the coordination of formate with the oxidised active site, displacing the hydroxyl group (reassigned to a sulfido group in later studies) [22]. Subsequently, the formate ion is oxidised to CO2 either by the proton moving to His141, coupled with one-electron transfer to Mo ion, followed by the same proton moving to Sec140 together with another electron transfer to Mo, or by the proton moving directly to Sec140 and the transfer of two electrons to Mo (cf. reaction 1 in Scheme 1).
However, in the reinterpretation of the crystal structure by Raaijmakers and Romão, a new reaction mechanism was suggested (reaction 2 in Scheme 1) [23]. In this, the Sec/Cys residue dissociates and formate binds to Mo. After that, the proton of formate is abstracted by His141 and two electrons are transferred to Mo simultaneously [23]. On the other hand, a sulfur-shift reaction mechanism has been suggested based on computational studies (reaction 3 in Scheme 1) [39,40,41]. In the first step of this mechanism, the Sec/Cys ligand dissociates from Mo ion and the sulfido group then forms a bond to the Se/S atom of Sec/Cys. In this process, the Mo(VI) ion is reduced to Mo(IV). This leads to a vacant coordination position, which is taken by the formate substrate. In the next step, cleavage of Se/S–S bond results in the free ionic form of Sec/Cys, which can abstract a proton from formate [39,40,41,42].
In another computational study by Tiberti et al. [42], the formate ion first binds to Mo by displacing the Sec group (reaction 4 in Scheme 1). Then, Mo abstracts a hydride ion from formate, giving a Mo–H species. This involves a cleavage of the Mo–O bond and formation of a Mo–H bond. Next, the hydride moves as a proton to the sulfido group, with the concomitant reduction of Mo. Finally, a fifth reaction mechanism was recently proposed based on the experimental data (reaction 5 in Scheme 1) [31, 43]. In this, the formate substrate enters the oxidised active site, without coordinating with Mo, but instead resides in the second coordination sphere, where the sulfido group can abstract a hydride ion, yielding Mo(IV)–SH.
In this study, we have studied and compared these five reaction mechanisms of FDH with the computational QM/MM approach. This allows us to decide which is the most likely mechanism and to discuss how the protein affects the reaction energies, thereby providing an improved understanding of the function of the FDHs.
Methods
The protein
All calculations were based on the 1.6-Å crystal structure of formate dehydrogenase (FDH N) from Escherichia coli (PDB code 1KQF) [25]. There are three subunits in this enzyme, A, B and C: the Mo centre and one of the [4Fe–4S] clusters are located in subunit A, four [4Fe–4S] clusters are in subunit B, and two heme groups are in subunit C. In this paper, we included only subunit A in the calculations. The substrate formate was added to the active site because it is missing in the crystal structure. In addition, we replaced Sec196 by Cys.
The setup of the enzyme was the same as in our previous calculations [44, 45]. The protonation states of all the residues were determined by a study of the solvent accessibility, the hydrogen-bond pattern, and the possible formation of ionic pairs; it was checked by PROPKA [46] calculations. All Arg, Lys, Asp, and Glu residues were assumed to be charged. Cysteine ligands coordinating with metals were deprotonated. Among the His residues, His84, 197, 216, 237, 356, 367, 658, 849, 900, and 907 were assumed to be protonated on NE2 atom, His448, 902, and 975 were assumed to be protonated on ND1, whereas the others were modelled as doubly protonated. His197 is close to the active site and forms a hydrogen bond with the OG1 atom of Thr200. One of the molybdopterin ligands (MGD1018) was modelled with both phosphate groups singly protonated (because it does not have any nearby positively charged residues), whereas both phosphate groups of the other molybdopterin ligand (MGD1019) were fully deprotonated (because all four O atoms accept hydrogen bonds from surrounding residues and there are one Lys and two Arg residues close to it).
The protein was protonated and solvated with water molecules forming a sphere with a radius of 53 Å around the geometric centre using the leap module of the Amber software package (~ 57,000 atoms in total) [47]. The added protons and water molecules were optimised by 120-ps simulated annealing calculations, followed by a minimisation, keeping the other atoms fixed at their crystal-structure positions.
QM calculations
All QM calculations were performed with the Turbomole 7.0 software [48]. The TPSS [49] and B3LYP [50,51,52] density functional theory methods were employed for all calculations and two different basis sets were used, viz. def2-SV(P) [53] and def2-TZVP [54]. Test calculations were performed also with the def2-TZVPD [55] basis set but the difference was small, ~ 1 kJ/mol. The calculations were sped up by expanding the Coulomb interactions in an auxiliary basis set, the resolution-of-identity (RI) approximation [56, 57].
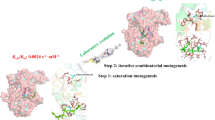
All the calculations used a QM system (shown in Fig. 1) consisting of the Mo ion with all the first-sphere ligands (sulfido, Cys196, and the two MDG molecules), four residues from the second sphere of Mo, His197, Arg446, Ile451 and Asn191, and the formate substrate. For Ile451 and Asn191, we truncated the QM region between the CA and CB atoms. The full Cys196 and His197 residues were included in the QM region and the junctions were between the backbone CA and C atoms in Val195 and the N and CA atoms in Gly198. Arg446 was truncated between CA and CB atoms. The MDG groups were truncated between the C10 and C11 atoms, so that the full pyranopterin system was included, but not the phosphate groups and the nucleotide. These large models allow a great flexibility in the active site, which is needed in several of the suggested mechanisms. The second-sphere residues also affected the energies significantly. The QM system in our calculations is larger than in any previous QM calculation [39, 40, 42, 58]. It should be noted that all the groups in the QM system are conserved in all FDHs, except Ile451 and Asn191 [22,23,24, 32]. In some calculations of the sulfur-shift mechanism, an even larger model was used, in which the junction on Cys196 was moved two residues away (to give this residue a larger flexibility).
Thermal corrections to the Gibbs free energy (ΔΔGtherm), including the zero-point vibrational energy, were calculated at 298.15 K and 1 atm pressure using an ideal-gas rigid-rotor harmonic-oscillator approach [59] from vibrational frequencies calculated for a small model (involving the Mo ion, the formate ion, two dimethyldithiolene groups for MPT, and a methanethiol group for Cys196) in vacuum at the TPSS/def2-SV(P) level of theory. To obtain more stable results, low-lying vibrational modes (below 100 cm−1) were treated with the free-rotor approximation, using the interpolation model suggested by Grimme and implemented in the thermo program [60].
QM/MM calculations
The QM/MM calculations were performed with the ComQum software [61, 62]. In this approach, the protein and solvent are split into three subsystems: system 1 (the QM region) was relaxed by QM methods. It contained the same atoms as the QM-cluster calculations (Fig. 1). System 2 consisted of all the residues or water molecules within 6 Å of any atom in system 1 and was optionally relaxed by a full MM minimisation in each step of the QM/MM geometry optimisation. Finally, system 3 contained the remaining part of the protein and the solvent. It was kept fixed at the original (crystallographic) positions.
In the QM calculations, system 1 was represented by a wave function, whereas all the other atoms were represented by an array of partial point charges, one for each atom, taken from MM libraries. Thereby, the polarisation of the QM region by the surroundings is included in a self-consistent manner (electronic embedding). When there is a bond between systems 1 and 2 (a junction), the hydrogen link-atom approach was employed: the QM region was capped with hydrogen atoms (hydrogen link atoms, HL), the position of which is linearly related to the corresponding atom (carbon link atoms, CL) in the full system [61, 63]. All atoms were included in the point-charge model, except the CL atoms [64].
The total QM/MM energy in ComQum was calculated as [61, 62]
where \(E_{{{\text{QM}}1 + {\text{ptch}}23}}^{\text{HL}}\) is the QM energy of the QM region truncated by HL atoms and embedded in the set of point charge modelling systems 2 and 3 (but excluding the self-energy of the point charges). \(E_{{{\text{MM}}1,q_{1} = 0}}^{\text{HL}}\) is the MM energy of the QM system, still truncated by HL atoms, but without any electrostatic interactions. Finally, \(E_{{{\text{MM}}123,q_{1} = 0}}^{\text{CL}}\) is the classical energy of all atoms in the system with CL atoms and with the charges of the QM system set to zero (to avoid double counting of the electrostatic interactions). By this approach, which is similar to the one used in the ONIOM method [65], errors caused by the truncation of the QM system should cancel.
The geometry optimisations were continued until the energy change between two iterations was less than 2.6 J/mol (10−6 a.u.) and the maximum norm of the Cartesian gradients was below 10−3 a.u. The QM calculations were carried out using the Turbomole 7.0 software [48]. Geometry optimisation was performed using the TPSS [49] functional in combination with def2-SV(P) [53] basis set, including the empirical DFT-D3 dispersion correction in Turbomole [66]. The MM calculations were performed with the Amber software [47], using the Amber ff14SB field [67].
Molecular dynamics simulations
To further examine the sulfur-shift mechanism, molecular dynamics (MD) simulations were performed with Amber package [47]. The entire system was minimised by 1000 step, followed by 20-ps constant-volume equilibration and 20-ps constant-pressure equilibration. Then, 1-ns constant-pressure equilibration was performed. Finally, the 10-ns production simulation was carried out and coordinates were saved every 0.5 ps. In all simulations, the bonds between Mo ion and its ligands were restrained to the crystallographic values. Finally, the coordinates from MD simulation were used for QM/MM calculations.
Big-QM calculations
To obtain stable and converged energies, we employed the big-QM approach [44]. This method employs a QM system that includes all groups with at least one atom within 4.5 Å of a minimal QM region, consisting of the Mo ion and its first-sphere ligands. In addition, junctions were moved at least two residues away from the minimal QM system and all charged groups buried inside the protein were included, but the Fe–S cluster was omitted to avoid convergence problems. This gave a QM region of 1121 atoms, shown in Fig. 2, including residues 94, 107, 141, 179, 182, 190–199, 210, 219, 235–238, 259, 261, 264, 276, 280, 370, 409, 410, 413–415, 423, 445–448, 451, 456, 536, 557, 561–563, 565, 583, 588, 621, 631, 636, 649, 696, 775, 776, 809, 830, 834, 843, 848, 851, 854, 873, 881, 893–902, 906, 921, 944, 956, 974, 975, 988, 989, 992, 1002, 1005, 1006, MGD, the sulfido ligand, the Mo ion and formate. The big-QM calculations were performed on coordinates from the QM/MM calculations and with a point-charge model of the surroundings, because this gave the fastest calculations in our previous test [44]. To this big-QM energy, we added the DFT-D3 dispersion correction, calculated for the same big-QM region with Becke–Johnson damping [68], third-order terms, and default parameters for the TPSS functional using dftd3 program [66]. We also included a MM correction
yielding a standard QM/MM energy, but with the big-QM system as the QM region.
Total free energies used in the article to describe the reaction energy barrier are obtained as
Thus, they are based on the big-QM/MM energies with TPSS functional, including dispersion and the MM correction (\(E_{{{\text{bigQM}}/{\text{MM}}}}^{\text{SV(P)}}\)). This energy is then extrapolated to the B3LYP/def2-TZVP level using QM calculations with the normal QM region and including the point-charge model. Finally, entropic and thermal corrections are added.
Results and discussion
In this paper, we have studied the reaction mechanism of FDH. Geometries were obtained by QM/MM optimisations at the TPSS/def2-SV(P) level of theory with the surrounding protein outside the QM system (shown in Fig. 1) fixed at the crystal structure. To confirm that the structures are converged, we compared structures and energies with those obtained from QM/MM optimisations with all residues with at least one atom within 6 Å of any atom in the QM system optimised by MM. In addition, single-point big-QM calculations were carried out on the optimised geometries to obtain converged and reliable energies. We will first discuss issues regarding the initial state, e.g., whether the substrate coordinates with the Mo(VI) ion, if the cysteine ligand dissociates from the Mo and if the sulfur-shift mechanism is applicable for this enzyme. Then, the oxidation of formate is investigated, testing the five putative mechanisms shown in Scheme 1.
Substrate binding
In the crystal structure employed (PDB code: 1KQF [25]), no substrate is bound. The backbone N group of His448 forms a hydrogen bond with the sulfido group (S–N distance of 3.4 Å; cf. Fig. 1). There are three residues around the sulfido group, viz. Gln192, Ile451 and Asn191. There are also several water molecules close to the active site, which form a proton-transfer path from the active site to the solution. In addition, there is a hydrogen bond between ND1 of His197 and the carbonyl oxygen of Thr200 (N–O distance of 2.7 Å). There are also several groups around the Cys196 ligand. The side chain of Leu410 forms a close interaction (4 Å) with the sulfur atom of Cys196. Thr413 forms a hydrogen bond with the backbone O atom of Cys196 (O–O distance 2.7 Å). In addition, Cys196 is surrounded by His197. Thus, the active site is quite crowded.
In four of the suggested mechanisms, the formate substrate coordinates directly to the Mo ion in the first step. It does so by displacing either the sulfido group [22] or the cysteine ligand [23, 33, 39, 58]. However, the first suggestion was based on an incorrect crystal structure. Therefore, we did not investigate that suggestion. In the sulfur-shift mechanism [40, 41], the sulfido group and the Cys ligand first react to form a disulfide bond (with the concomitant reduction of Mo), leading to the dissociation of the SCys atom from Mo, leaving an open coordination site for formate.
For the binding of formate displacing the Cys ligand, we first tried to cleave the Mo–SCys bond, but it always re-formed during the optimisation, even if we started from structures with formate bound to Mo and employed restraints; as soon as the restraints were removed, the Cys ligand rebound to Mo and formate dissociated into the second coordination sphere. Thus, we have not been able to find any stable low-energy structure with formate coordinated with Mo. This is in accordance with some recent suggestions [31, 43].
On the other hand, a reasonable structure could be found with formate bound in the second coordination sphere of Mo, as can be seen in Fig. 1 (this state will be called RS in the following). One of the carboxylate atoms (OS1) forms a strong hydrogen bond to the backbone H atom of His197, whereas the proton is directed towards the sulfido ligand. The Arg446, His197, Ile451, and Asn191 residues surround the substrate, placing it in a proper position for the next step in the reaction mechanism.
To study the sulfur-shift mechanism [39,40,41], we used a larger QM region (Fig. 3) to allow extensive flexibility of the model (initial studies with the normal model gave only high-energy structures). With this large QM region, a species with the substrate binding to Mo ion and a disulfide bond between the sulfido group and the Cys ligand could be found (Fig. 3, named the S-shift species). However, this species was 260 kJ/mol higher (129 kJ/mol with system 2 relaxed) in energy than the RS species. Owing to the large difference in the energies obtained with system 2 fixed or relaxed, we run MD simulations to further relax the surrounding residues and solvent, which were followed by QM/MM calculation with the large QM region, using geometries taken from snapshot of the MD simulation. Because the surrounding protein and water solvent moved in the MD simulation, the QM/MM energies are not comparable. However, by comparing only the energies of the QM region in vacuum, it can be concluded that the S-shift species is still 157 kJ/mol higher in energy than RS. Thus, our results strongly indicate that the sulfur-shift mechanism is not possible in the protein (i.e., that the protein is constructed to avoid such a mechanism).
This is in contrast to previous QM calculations, which suggested that the sulfur-shift mechanism is favourable [39,40,41]. However, these studies were based on QM-cluster calculations, in which the surrounding protein was ignored. In the original study by Ramos and coworkers [40], all atoms were allowed to move freely and a low activation energy of 29 kJ/mol was obtained for the formation of the S–S bond. It should be noted that the Arg333 was at a position that is not supported by the crystal structure in their calculations. However, in another study by Cerqueira and coworkers with the same QM region, but with some atoms in the periphery frozen during the geometries optimisation (to model constraints of the surrounding protein) [39], the activation energy increased to 84 kJ/mol, showing that the results depend strongly on these constraints.
We also tried to run QM-cluster calculation with different models (Table S1). With the small model used by Ramos and coworkers (MPT modelled by dimethyldithiolene, but without Arg333, because there is no such residue in our crystal structure; Figure S1) [40], the S-shift species was 27 kJ/mol higher in energy than the RS species. With the large model for the MPT ligand, shown in Fig. 3, the gap decreased to 0.3 kJ/mol. However, if the same model is optimised in the protein with QM/MM calculations, the S-shift species was 176 kJ/mol higher than RS, with a very large MM correction (72 kJ/mol), but a modest effect of the point charges (28 kJ/mol). As can be seen from Fig. 1, Cys196 is surrounded by Leu410 and His197, and there is not much space for it to move. Therefore, we believe that the QM/MM optimisations give more reliable and relevant structures than QM-cluster calculations, showing that the sulfur-shift mechanism is strongly disfavoured by the protein.
Reaction mechanism of formate dehydrogenase
The results in the previous section showed that only a single low-energy substrate-bound structure was found, RS, with the substrate in the second coordination sphere. Starting from this structure, two possible reactions were tested, viz. proton abstraction by the sulfide ion or by SCys. However, in the latter case, no proton transfer could be obtained; instead the proton always returned to the formate ion after geometry optimisation. On the other hand, a favourable mechanism could be obtained with the sulfido group as the proton acceptor. As can be seen in Fig. 1, the proton on the substrate (HS) is close to the S2− group in the starting structure, 2.16 Å. Therefore, HS could easily be transferred to S2−.
Previous computational studies of FDH with the QM-cluster approach included only three conserved residues in the QM region, viz. Cys196, His197 and Arg446 in our structure [39, 58]. We used the same QM region in our preliminary calculations. However, we found that such a QM region was not large enough to give converged structures and energies (Table 1). In particular, the QM/MM energies changed by 31–45 kJ/mol if system 2 was relaxed. We solved this problem by enlarging the QM region to that in Fig. 1. Looking at the largest contributions to the difference between the QM/MM calculations with and without system 2 fixed, we found that Ile451 and Asn191, which are close to the substrate, made the largest movements. Therefore, we included them in the QM region to make the results more stable. However, it should be noted that these two residues are not conserved among all FDHs, making it unclear how transferable this QM region is to other FDHs.
With this QM region, we studied the oxidation of formate to CO2 on FDH. In some experimental studies, a hydride transfer from formate to the sulfido group has been suggested [31, 43]. In addition, EPR spectroscopic studies have found a Mo(V) signal [43]. Our QM/MM calculations confirm that the mechanism is hydride-transfer reaction. As is shown in Fig. 4, a transition state (TS) and an intermediate state (IM) were located for the transfer of the proton from formate to the sulfide ion with a concomitant transfer of two electrons to Mo. Interestingly, this did not give rise to the CO2 product, but instead the product reacted with the sulfur atom of Cys196, forming a thiocarbonate group, which is at the same oxidation level (IV). Thus, the oxidation state of Mo ion is +VI in RS state and it is reduced to +IV after the hydride transfer.
Key bond distances for these three states are collected in Table 2. For the RS state, the SS–HS bond is 2.16 Å, and the HS is ready to transfer to sulfido group. The Mo–SS distance is 2.23 Å and the Mo–SCys distance is 2.45 Å, indicating that there is a double bond between the Mo and SS atoms but a single bond between Mo and SCys. The Mo–S bonds to the sulfur atoms of the molybdopterin ligands Mo are 2.46–2.48 Å, except Mo–S3, which is 2.38 Å. For the transition state, the CS–HS bond (CS is the carbon atom in the formate substrate) is 1.32 Å and SS–HS is 1.60 Å (SS is the sulfide ion), which are 0.18 Å longer and 0.46 shorter than in RS state, respectively. The Mo–SS distance is 2.28 Å, which is 0.05 Å longer than in RS state. The Mo–SCys bond is 0.02 Å longer, whereas the Mo–S bonds with MPT are 0.1–0.3 Å shorter, except the Mo–S3 bond, which is 0.02 Å longer. For the IM state, the CS–HS bond is cleaved and the SS–HS bond has formed. The Mo–SS and Mo–SCys bonds are 0.16 and 0.07 Å longer than in TS state.
In the first step of the reaction mechanism, the activation barrier is 28 kJ/mol and IM is 39 kJ/mol more stable than the RS state. As shown in Table 3, QM/MM calculations with and without system 2 fixed gave a difference of 15 kJ/mol for TS and 1 kJ/mol for IM state, indicating that the residues in system 2 did not affect the energies significantly. The basis set effect (between def2-SV(P) and TZVP) is small, 0–4 kJ/mol. Calculations with the B3LYP functional give a 12 kJ/mol higher TS and 15 kJ/mol lower IM state than the TPSS functional. For the big-QM calculations, the energy barrier is 16 kJ/mol and the reaction is exothermic by 16 kJ/mol. The MM correction is 2–8 kJ/mol, whereas the dispersion correction is minimal (0.1–0.2 kJ/mol). The thermal correction is negative and quite small, 4–5 kJ/mol.
Product release
As mentioned above, the CO2 product was not released, but was bound to SCys in the IM state as a thiocarbonate ion. In fact, if we try to cleave the SCys–C bond, the RS state is re-formed. In this process, the energy increased to 51 kJ/mol (relative to IM at the B3LYP/def2-TZVP level of theory) when SCys–C distance was stretched to 2.6 Å, which is consistent with the forward reaction from RS to IM. We studied also the cleavage at the TPSS/def2-TZVP and B3LYP/de2-SV(P) level of theory, but both calculations predicted that IM was re-formed when the restraint was released. The same was the case if the surrounding protein was allowed to relax in the calculations. Therefore, we investigated whether the product release was facilitated by oxidising the active site (remember that two electrons need to be removed from Mo to return the active site to the starting state). It is noteworthy that the release of CO2 also seems to be necessary before the proton on the sulfido ligand may move out the active site, because there is no apparent way to transfer it to solution as long as CO2 binds to Cys196.
First, we removed one electron from the QM system, resulting in the +V oxidation state of Mo, which has been observed in an EPR study [43]. The resulting structure (IM2) in Fig. 5 shows that the substrate is still bound to SCys. Moreover, the product release was still strongly uphill (e.g., 82 kJ/mol relative to the IM2 state at the B3LYP/def2-TZVP level when the CS–SCys distance was constrained to 3.8 Å) and the structure returned to the IM2 if the restraint was released. The same applied if the calculations were performed at the TPSS/def2-TZVP and B3LYP/def2-S(P) levels of theory.
However, when another electron was removed from the active site, to form the Mo(VI) state, a species (PS, also shown in Fig. 5) with a CS–SCys distance of 2.8 Å was obtained, indicating an essentially released CO2 product (this distance is 2.0 and 2.1 Å in IM and IM2), which is also confirmed by the O–C–O angle which was 168° compared to 133° and 132° in IM and IM2.
For the IM species, we also tried to form the product by hydrolysis with H2O, forming carbonic acid. In the crystal structure, there are several water molecules close to the CO2 molecule. The three closest were included in the QM region. One of them was allowed to attack the CO2, but the activation energy was too high, 300 kJ/mol.
Thus, our results indicate that the CO2 product is not released until the active site is re-oxidised to the starting Mo(VI) state. To check this suggestion, we studied the simple reaction CH3S− + CO2 → CH3SCO2−, i.e., the formation of a thiocarbonate anion from CO2 and a simple model of Cys196. At the TPSS-D3/def2-SV(P) level of theory (used for our geometry optimisations), the reaction energy is −129 kJ/mol, showing that the formation of the thiocarbonate ion is strongly favourable. However, this effect is reduced by a larger basis set and by solvation effects, whereas the effect of the DFT method is restricted, so that at the B3LYP-D3/def2-TZVPD level in a COSMO solvent with a dielectric constant of 80 (modelling water), the reaction energy is only −47 kJ/mol.
Moreover, it is also counteracted by the entropy, because two molecules are converted to a single product. Thermal corrections to the Gibbs free energy (calculated from vibrational frequencies obtained at the TPSS-D3/def2-SV(P) level of theory) amount to +46 kJ/mol, so that the reaction becomes essentially thermoneutral in water solution (−1 kJ/mol).
Since both solvation and entropy effects are hard to estimate accurately for enzyme reactions, we need to conclude that the suggestion that a thiocarbonate intermediate is formed and that the active site needs to be oxidised twice before CO2 is released is rather weak. In particular, it is not needed for the suggested second-sphere mechanism of the formate reaction.
Conclusions
In this paper, we have studied the reaction mechanism of formate dehydrogenase with the QM/MM approach. Our results indicate that formate substrate does not bind directly to the Mo ion, but instead resides in the second coordination sphere. There, it transfers the proton to the sulfido group, while two electrons are transferred to Mo. Initially, the CO2 product forms a thiocarbonate group with the Cys ligand. This step is quite favourable with an activation energy of 28 kJ/mol and a reaction energy of −39 kJ/mol. However, the CO2 product cannot be released until the active site is oxidised by two electrons.
The QM region in our QM/MM calculations is larger than in previous computational studies [39, 40, 42, 58]. We compared the calculations with a small QM region (without Ile451 and Asn191) to those with large QM region and found the two residues are important for the energies. In fact, with a fixed MM system, the QM/MM energy barrier was 85 kJ/mol lower with the two residues in the QM system. However, these two residues are not conserved in all FDHs. Therefore, the size of QM region needs to be carefully selected in QM studies of FDHs. To obtain accurate and stable energies, we performed big-QM calculations with 1121 atoms, which lowered the energies by 20–38 kJ/mol.
References
Pierre AC (2012) Chem Eng 2012:1–22
Mikkelsen M, Jorgensen M, Krebs FC (2010) Energy Environ Sci 3:43–81
DiCosimo R, McAuliffe J, Poulose AJ, Bohlmann G (2013) Chem Soc Rev 42:6437–6474
Appel AM, Bercaw JE, Bocarsly AB, Dobbek H, DuBois DL, Dupuis M, Ferry JG, Fujita E, Hille R, Kenis PJA, Kerfeld CA, Morris RH, Peden CHF, Portis AR, Ragsdale SW, Rauchfuss TB, Reek JNH, Seefeldt LC, Thauer RK, Waldrop GL (2013) Chem Rev 113:6621–6658
Alissandratos A, Kim HK, Easton CJ (2013) Bioengineered 4:348–350
Mondal B, Song JS, Neese F, Ye SF (2015) Curr Opin Chem Biol 25:103–109
Sakakura T, Choi JC, Yasuda H (2007) Chem Rev 107:2365–2387
Hille R, Hall J, Basu P (2014) Chem Rev 114:3963–4038
Maia LB, Moura JJG, Moura I (2015) J Biol Inorg Chem 20:287–309
Hartmann T, Schwanhold N, Leimkuhler S (2015) Biochim Biophys Acta Proteins Proteom 1854:1090–1100
Jormakka M, Byrne B, Iwata S (2003) Curr Opin Struct Biol 13:418–423
Kato N (1990) Methods Enzymol 188:459–462
Vinals C, Depiereux E, Feytmans E (1993) Biochem Biophys Res Commun 192:182–188
Popov VO, Lamzin VS (1994) Biochem J 301:625–643
Filippova EV, Polyakov KM, Tikhonova TV, Stekhanova TN, Boiko KM, Popov VO (2005) Crystallogr Rep 50:796–800
Shabalin IG, Polyakov KM, Tishkov VI, Popov VO (2009) Acta Naturae 1:89–93
Alekseeva AA, Savin SS, Tishkov VI (2011) Acta Naturae 3:38–54
Maia LB, Moura I, Moura JJG (2017) Inorg Chim Acta 455:350–363
Zinoni F, Birkmann A, Stadtman TC, Bock A (1986) PNAS 83:4650–4654
Axley MJ, Grahame DA, Stadtman TC (1990) J Biol Chem 265:18213–18218
Gladyshev VN, Boyington JC, Khangulov SV, Grahame DA, Stadtman TC, Sun PD (1996) J Biol Chem 271:8095–8100
Boyington JC, Gladyshev VN, Khangulov SV, Stadtman TC, Sun PD (1997) Science 275:1305–1308
Raaijmakers HCA, Romao MJ (2006) J Biol Inorg Chem 11:849–854
Jormakka M, Tornroth S, Byrne B, Iwata S (2002) Science 295:1863–1868
Jormakka M, Tornroth S, Abramson J, Byrne B, Iwata S (2002) Acta Crystallogr Sect D Biol Crystallogr 58:160–162
Pommier J, Mandrand MA, Holt SE, Boxer DH, Giordano G (1992) Biochim Biophys Acta 1107:305–313
Plunkett G, Burland V, Daniels DL, Blattner FR (1993) Nucleic Acids Res 21:3391–3398
Abaibou H, Pommier J, Benoit S, Giordano G, Mandrandberthelot MA (1995) J Bacteriol 177:7141–7149
Costa C, Teixeira M, LeGall J, Moura JJG, Moura I (1997) J Biol Inorg Chem 2:198–208
Rivas MG, Gonzalez PJ, Brondino CD, Moura JJG, Moura I (2007) J Inorg Biochem 101:1617–1622
Maia LB, Fonseca L, Moura I, Moura JJG (2016) J Am Chem Soc 138:8834–8846
Raaijmakers H, Macieira S, Dias JM, Teixeira S, Bursakov S, Huber R, Moura JJG, Moura I, Romao MJ (2002) Structure 10:1261–1272
Schrapers P, Hartmann T, Kositzki R, Dau H, Reschke S, Schulzke C, Leimkuhler S, Haumann M (2015) Inorg Chem 54:3260–3271
George GN, Colangelo CM, Dong J, Scott RA, Khangulov SV, Gladyshev VN, Stadtman TC (1998) J Am Chem Soc 120:1267–1273
George GN, Costa C, Moura JJG, Moura I (1999) J Am Chem Soc 121:2625–2626
Khangulov SV, Gladyshev VN, Dismukes GC, Stadtman TC (1998) Biochemistry 37:3518–3528
Maia LB, Moura I, Moura JJG (2017) EPR spectroscopy on mononuclear molybdenum-containing enzymes. In: Hanson G, Berliner L (eds) Future directions in metalloprotein and metalloenzyme research. Biological Magnetic Resonance, vol 33. Springer, Cham
Maia LB, Moura I, Moura JJG (2016) Molybdenum and tungsten-containing enzymes: an overview. In: Hille R, Schulzke C, Kirk ML (eds) Molybdenum and tungsten enzymes: biochemistry. The Royal Society of Chemistry, Cambridge, pp 1–80
Mota CS, Rivas MG, Brondino CD, Moura I, Moura JJG, Gonzalez PJ, Cerqueira NMFSA (2011) J Biol Inorg Chem 16:1255–1268
Cerqueira NMFSA, Fernandes PA, Gonzalez PJ, Moura JJG, Ramos MJ (2013) Inorg Chem 52:10766–10772
Cerqueira NMFSA, Gonzalez PJ, Fernandes PA, Moura JJG, Ramos MJ (2015) Acc Chem Res 48:2875–2884
Tiberti M, Papaleo E, Russo N, De Gioia L, Zampella G (2012) Inorg Chem 51:8331–8339
Niks D, Duvvuru J, Escalona M, Hille R (2016) J Biol Chem 291:1162–1174
Hu L, Söderhjelm P, Ryde U (2013) J Chem Theory Comput 9:640–649
Dong G, Ryde U (2016) J Biol Inorg Chem 21:383–394
Olsson MHM, Søndergaard CR, Rostkowski M, Jensen JH (2011) J Chem Theory Comput 7:525–537
Case DA, Berryman JT, Betz RM, Cerutti DS, Cheatham TE III, Darden TA, Duke RE, Giese TJ, Gohlke H, Goetz AW, Homeyer N, Izadi S, Janowski P, Kaus J, Kovalenko A, Lee TS, LeGrand S, Li P, Luchko T, Luo R, Madej B, Merz KM, Monard G, Needham P, Nguyen H, Nguyen HT, Omelyan I, Onufriev A, Roe DR, Roitberg A, Salomon-Ferrer R, Simmerling CL, Smith W, Swails J, Walker RC, Wang J, Wolf RM, Wu X, York DM, Kollman PA (2014) AMBER 14. University of California, San Francisco
TURBOMOLE V70 (2015) A development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com
Tao J, Perdew JP, Staroverov VN, Scuseria GE (2003) Phys Rev Lett 91:146401
Becke AD (1988) Phys Rev A 38:3098–3100
Lee CT, Yang WT, Parr RG (1988) Phys Rev B 37:785–789
Becke AD (1993) J Chem Phys 98:5648–5652
Schäfer A, Horn H, Ahlrichs R (1992) J Chem Phys 97:2571–2577
Weigend F, Ahlrichs R (2005) Phys Chem Chem Phys 7:3297–3305
Rappoport D, Furche F (2010) J Chem Phys 133:134105
Eichkorn K, Treutler O, Öhm H, Häser M, Ahlrichs R (1995) Chem Phys Lett 240:283–290
Eichkorn K, Weigend F, Treutler O, Ahlrichs R (1997) Theor Chem Acc 97:119–124
Leopoldini M, Chiodo SG, Toscano M, Russo N (2008) Chem Eur J 14:8674–8681
Frank J (2017) Introduction to computational chemistry. Wiley, Chichester, pp 454–464
Grimme S (2012) Chem Eur J 18:9955–9964
Ryde U (1996) J Comput Aided Mol Des 10:153–164
Ryde U, Olsson MHM (2001) Int J Quantum Chem 81:335–347
Reuter N, Dejaegere A, Maigret B, Karplus M (2000) J Phys Chem A 104:1720–1735
Hu L, Söderhjelm P, Ryde U (2011) J Chem Theory Comput 7:761–777
Svensson M, Humbel S, Froese RDJ, Matsubara T, Sieber S, Morokuma K (1996) J Phys Chem 100:19357–19363
dftd3 software. http://www.thchuni-bonnde/tc/indexphp?section=downloads&subsection=DFT-D3. Accessed 1 Aug 2018
Maier JA, Martinez C, Kasavajhala K, Wickstrom L, Hauser KE, Simmerling C (2015) J Chem Theory Comput 11:3696–3713
Grimme S, Ehrlich S, Goerigk L (2011) J Comput Chem 32:1456–1465
Acknowledgements
This investigation has been supported by grants from the Swedish research council (project 2014-5540), the China Scholarship Council, the Royal Physiographic Society in Lund and COST through Action CM1305 (ECOSTBio). The computations were performed on computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University. We acknowledge fruitful discussions with Prof. Silke Leimkühler, Potsdam.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dong, G., Ryde, U. Reaction mechanism of formate dehydrogenase studied by computational methods. J Biol Inorg Chem 23, 1243–1254 (2018). https://doi.org/10.1007/s00775-018-1608-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00775-018-1608-y