1 Introduction

An unmanned underwater vehicle (UUV) is a type of robot designed to operate underwater without the need for human intervention. The primary role of UUV’s is to perform tasks that are difficult, dangerous, or impossible for human divers to undertake. UUV’s play an increasingly important role in a range of underwater activities, from scientific research to military purposes, maritime surveillance, and exploration of marine resources, such as biological organisms, chemicals, minerals, and natural gas. The current technology has allowed UUV’s to excel at tasks including underwater detection, tracking, and rescue.

With the increasing complexity and diversity of underwater tasks, UUV demanded the capability to travel a long distance in a short period of time and with a high accuracy in motion control. An UUV’s propulsion system should be designed considering the UUV’s maneuverability, as precise and swift movements underwater are critical for a UUV, enabling the UUV to easily change direction and speed to navigate complex environments and complete challenging tasks. The propulsion system of UUV’s can be classified into two groups based on the propulsor, i.e., a screw propeller or a jet. The propeller propulsion system has traditionally been used in most UUV designs because of its stability and convenience for operation. Such designs have a characteristic that can generate constant thrust, so they can be used in environments where there is no space constraint or continuous work is required [1, 2]. However, a propeller can cause rotational energy loss which is unavoidable no matter how optimized it is. In addition, at low speeds and in tight spaces, the maneuvering performance degrades significantly. A jet propulsion system was loosely inspired by marine animals like jellyfish and squid. This propulsion device can be simplified into a system consisting of a piston and a nozzle. Thrust is produced by the piston pushing water. As the piston moves along the thrust direction during the stroke, there is no rotational energy loss. It can achieve relatively higher efficiency than the propeller propulsion system. In addition, it offers advantages such as low noise generation, great attitude control, and enhanced maneuvering performance [3].

Several researchers have applied jet propulsion systems to underwater vehicles. Xin et al. [4] used a waterjet system for an autonomous underwater vehicle. Based on the six-degrees-of-freedom nonlinear dynamic equations of the vehicle motion, they investigated the vehicle’s response to various vectoring angles. The results indicated that the thrust components responsible for yaw and pitch control could reach a high level of maneuvering performance with a low thrust deduction when the vectoring angle was changed. These results suggested that a jet propulsion system could achieve precise attitude control. Zhang et al. [5] adopted a high-pressure jet propulsion system with a thrust vector control system (TVCS) to improve the maneuverability of underwater vehicles. They conducted turning circle tests with the change of sailing speeds, and the results showed that the tactical diameter was independent of the sailing speed. The case with the fastest sailing speed took the shortest time to complete the turning circle maneuver, but the advance and transfer times were greater, and the distance was longer. Their studies concluded that underwater vehicles that adopted a jet propulsion system with TVCS showed good maneuverability at various speed conditions.

During the periodic motion of contraction and relaxation in a jet propulsion system, it is often accompanied by the generation of a vortex ring. The resulting vortex can then be manipulated to produce a net forward or backward thrust, depending on the direction of the jet and the orientation of the vortex. Such a device is called a vortex ring thruster (VRT). When the piston contracts, vortex rings are formed behind the VRT exit, resulting in an axisymmetric velocity distribution between the center of the nozzle and the nozzle wall. Many studies have dealt with experiments and numerical simulations for these vortex rings. Gharib et al. [6] demonstrated that a time scale with a narrow range of values characterized the formation of vortex rings in the water tank. Their studies concluded that the disconnection of the leading vortex ring from the trailing jet occurred at a critical stroke ratio, which they called the formation number. They measured the velocity and vorticity fields of vortex rings using the digital particle image velocimetry. They showed that the formation numbers of vortex ring are in the range of 3.6 to 4.5. For the case of a stroke ratio greater than four, they observed an apparent trailing jet followed by vortex rings. The process for termination of flux into the vortex ring is called pinch-off, which separates the vortex ring and the trailing jet. Rosenfeld et al. [7] performed CFD simulations under the same conditions as Gharib et al. [6]. It was confirmed that the formation number was approximately four, which was in good agreement with the experiment of Gharib et al. [6]. They also found that the formation number depended on the velocity profile at the exit of the piston.

In many previous studies, CFD simulations have also been conducted to accelerate or delay the formation number of vortex rings by varying different conditions. Dabiri and Gharib [8] presented experimental results that the pinch-off process was delayed by approximately 10% by imposing a bulk axisymmetric counter-flow during vortex ring formation. They insisted that retardation of formation number led to an increase in propulsion performance. Krueger et al. [9] investigated the formation of vortex rings in uniform background co-flow, and it is the opposite setting compared to the experiments of Dabiri and Gharib [8]. They measured vortex ring circulation and the formation time that it took for them to form during pinch-off process, for the co-flow to jet velocity ratio, \(R_{v}\). In the case of \(R_{v} > 0.5\), the vortex ring pinch-off process occurred almost immediately following the vortex ring’s formation. Also, experiments were conducted by Dabiri and Gharib [10] to observe the evolution and pinch-off process of the leading vortex ring in the case of a time-dependent exit diameter. They showed that formation time could be delayed with temporally varying exit diameters.

Since a VRT has advantages such as low power consumption, increased maneuverability, and cost-effective in previous studies, studies on applying it as a propulsion system for the UUV have been conducted [11, 12]. However, there is a limitation to the application of the VRT to UUVs due to limited speed and operational range, as well as their low maneuvering and propulsion performance in tightly enclosed spaces and shallow seas. In this study, the Coanda effect was adopted to the VRT to improve the propulsion performance as well as maneuvering performance.

The Coanda effect is a phenomenon in fluid dynamics that occurs when a fluid flows over a curved surface and follows the contour of the surface. This effect is due to the reduction in pressure on the curved surface, which causes the fluid to adhere to the surface and flow around it. Newman [13] experimented to confirm the Coanda effect using a jet along a two-dimensional circular cylinder surface. The fluid attached itself to a curved wall and adhered to nearby surfaces due to the lower static pressure along the curved surface than the ambient pressure. Many studies have been carried out using the Coanda effect regarding flow control and thrust vectoring [14,15,16]. From the flow control perspective, as the jet was attached to control flows around the curved surface, it caused the generation of additional momentum due to the injected fluid. Englar [17] showed that the lift increased and drag decreased as the jet was attached near the leading edge of a elliptic configuration. Amitay et al. [18] investigated the reattachment of separated flow on an airfoil using synthetic jet actuators. In a case without synthetic jet actuators, the airfoil stalled for an angle of attack greater than five degrees. However, for less than 17.5 degrees, a fully attached flow can be obtained when the synthetic jet actuators were applied. As a result, they obtained up to 100% lift augmentation and up to 45% pressure drag reduction thanks to flow reattachment. Banazadeh and Saghafi [19] designed and developed a nozzle for multi-directional thrust vectoring using the Coanda effect. The quasi-Newton optimization was employed to find optimal nozzle geometry. The optimized nozzle showed an approximately 32% improvement in thrust vector angle compared to the conventional nozzle. Allen and Smith [20] conducted experiments to introduce a novel spray method using the Coanda effect for axisymmetric geometries through the interaction of two jets. One was a primary jet, and the other was a control jet. The control jet was parallel to the primary jet and was adjacent to the curved collar. They confirmed the effect of the thrust vectoring with the change of momentum ratio of the primary jet to the control jet. They found that the exit slot area of the control jet greatly affected the maximum vector angle and the momentum ratio. Recently, the Coanda effect has been applied to a variety of electronic products such as air conditioners, air purifiers, refrigerators, and hair dryers. There is a wind-free air conditioner that, when the cool air exits and touches a curved cooling panel, accelerates and escapes more quickly into the room. Air purifiers also apply curved panels to circulate clean air quickly indoors. In refrigerators, this principle is used to spread cold air rapidly inside. Dyson has designed the Coanda Smoothing Dryer with a semi-circular nozzle for hair stylers. The round nozzle creates a stronger airflow than flat nozzles, and when brought close to the hair, it automatically wraps around the device, allowing for hair styling.

In the present study, we performed CFD simulations on a regular VRT and a CoVoRT, using SNUFOAM, which was developed to evaluate the propulsion performance of a VRT using a CFD toolkit with open-source libraries. The simulations of a CoVoRT were conducted with different Coanda wall curvature radii, the speed ratio of the primary jet to the Coanda jet, the Coanda jet exit height, stroke ratio, and velocity function, which include acceleration and deceleration phase. These results substantiated the feasibility of implementing CoVoRT within UUV’s for diverse operational applications. Moreover, the CFD data are anticipated to serve as reliable verification benchmarks for the model test results.

2 Computational methods

Previous studies [7, 13] adopted a relatively low piston velocity. The governing equations were the continuity and the Navier–Stokes equations for unsteady, laminar, incompressible flow, which are expressed as

$$\frac{{\partial u_{i} }}{{\partial x_{i} }} = 0,$$
(1)
$$\frac{{\partial u_{i} }}{\partial t} + u_{j} \frac{{\partial u_{i} }}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {\nu \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right),$$
(2)

where \(u_{i}\) is the velocity in three-axial directions (\(i = x,y,z\)), \(\rho\) is the fluid density. \(p\) is the static pressure, and \(\nu\) is the fluid kinematic viscosity.

The Crank–Nicolson scheme was applied with a second-order accuracy for temporal discretization. For spatial discretization, the Gauss linear scheme to achieve second-order accuracy for divergence and Laplacian terms was used. For pressure–velocity coupling, the PIMPLE algorithm was adopted, which is the merged semi-implicit method for pressure linked equations (SIMPLE) algorithm and pressure implicit with the splitting of operator (PISO) algorithm [21]. The computational methods are summarized in Table 1.

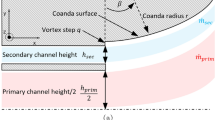
Table 1 Summary of computational methods
Full size table

The computational domains for a VRT and a CoVoRT are illustrated in Fig. 1.

Fig. 1
figure 1

Computational domains for a VRT and b CoVoRT

Full size image

A piston-cylinder mechanism was used to simulate the VRT and the CoVoRT. The computational domains for the VRT and the CoVoRT are axisymmetric, and the piston diameter \(\left( {D_{p} } \right)\), piston maximum stroke \(\left( {L_{p} } \right)\), and maximum piston stroke ratio \(\left( {L_{m} /D_{p} } \right)\) are identical to those adopted for experiments of Gharib et al. [6]. The Coanda jet has different radii of curvature, one is the outer radius of curvature, \(R_{out}\), and the other is the inner radius of curvature, \(R_{in}\). The main dimensions of the VRT and the CoVoRT are shown in Table 2.

Table 2 Main dimensions of the VRT and the CoVoRT
Full size table

Concerning the boundary conditions, the Dirichlet boundary condition for the velocity was applied at the farfield. The no-slip boundary condition was imposed at the cylinder wall. To implement the piston motion, a fixed mass flow rate was adopted at the piston. For all simulations, a mass flow rate of the primary jet, denoted as \(\dot{m}_{p}\), of \(8.58 \times 10^{ - 4}\) kg/s, was used. The Neumann boundary condition for the pressure was applied to the piston, cylinder wall, and farfield. At the outlet boundary, the Dirichlet condition was applied for the pressure, while the Neumann condition was used for the velocity. The details of boundary conditions are shown in Fig. 2.

Fig. 2
figure 2

Boundary conditions of VRT and CoVoRT

Full size image

3 Results and discussion

To quantify the degree of numerical uncertainty in this study, we conducted preliminary simulations and calculated the grid convergence index (GCI) using a grid refinement ratio \(r_{G}\) of \(\sqrt 2\) in all directions, as recommended in previous studies [22, 23]. The coarse, medium, and fine grid distributions in the x and y directions are denoted as c, m, and f, respectively. Table 3 provides the details of the grid systems used in the preliminary simulations.

Table 3 Details of grid system for preliminary simulations
Full size table

For the grid convergence study, we selected the time-averaged kinetic energy in the x-direction over the entire domain and time-averaged pressure at a particular position located \(2D_{p}\) away from the piston exit in the x-axis direction. The grid convergence study involves multiple variables, which \(R_{G}\) denotes the convergence ratio, \(p_{G}\) is the apparent accuracy order, \(\delta_{RE}\) is the error derived using Richardson extrapolation, \(C_{G}\) represents the correction factor, and \(U_{G}\) denotes the uncorrected uncertainty. Roache [24] provides a comprehensive exposition on the definitions and methodologies for calculating these variables. The results of the grid convergence study for the VRT are summarized in Table 4.

Table 4 Results of the grid convergence study for the VRT
Full size table

To validate the computational methods used in this study, CFD simulations were performed under the same conditions as previous studies [6, 7, 25]. The grid density selected for this study was \(X_{m} Y_{m}\). Results from prior grid convergence tests demonstrated that this grid density offered minimal uncorrected uncertainty in each direction. Notably, Rosenfeld et al. [7] and Zhang et al. [25] used grids with dimensions of 151 × 121 and 1000 × 60 in the axial and radial directions, respectively. Figure 3 shows the non-dimensional total circulation and vortex ring circulation as a function of the formation time \(\left( {t^{*} } \right)\).

Fig. 3
figure 3

Comparison of the total and vortex ring circulation with the present results, CFD results by Rosenfeld et al. [7] and Zhang et al. [25], and experimental results by Gharib et al. [6]

Full size image

The change of total circulation and vortex ring circulation can reflect the evolution of vortex in the jet propulsion. The formation time is defined as

$$t^{*} = \frac{L}{{D_{p} }} = \frac{{U_{p} t}}{{D_{p} }},$$
(3)

where L is piston stroke, \(D_{p}\) is the diameter of primary cylinder, \(U_{p}\) is primary jet velocity, and t is the time.

The total circulation and the vortex ring circulation were calculated by integrating the vorticity in the whole computational domain and the interior region of the vortex ring, respectively. The total circulation increased linearly during the pushing stroke \(\left( {0 \le t^{*} \le 6} \right)\) and decreased slowly after stopping. Open symbols represent experimental data [6], and dashed and dash-double dotted lines represent CFD results of Rosenfield et al. (1998) and Zhang et al. [25], respectively. The present results (solid line) were identified in the previous CFD and experimental results. Table 5 shows the comparison of formation numbers between the present and previous results [6, 7]. The formation number is determined by the point in time when the maximum value of vortex ring circulation aligns with the total circulation curve. The formation number was predicted to be 3.74 under these flow condition, which was within 1.57% of previous results and close to those obtained from other CFD and experimental studies.

Table 5 Comparison of formation numbers with the previous results [6, 7]
Full size table

To further validate the present computational methods, the evolution of the discharged flow was compared with the previous CFD results [7] at three different formation times (\(t^{*} =\) 0.48, 1.44, and 3.84), as shown in Fig. 4. Rosenfeld et al. [7] used a grid density of \(151 \times 121\) in the axial and radial directions, respectively.

Fig. 4
figure 4

The evolution of the discharged flow velocity for the present and Rosenfeld et al. [7] depending on the different formation times

Full size image

The velocity profiles of the discharged flow were neither uniform nor parabolic but evolved over time and showed similar velocity profiles to those of Rosenfeld et al. [7] with a maximum error of about 2.6%. Figure 5 shows three vortex rings generated by three different maximum ratios and comparison with the experimental [6] and CFD results [25, 26].

Fig. 5
figure 5

Comparison of the present CFD result and previous results for vortex rings generated by three different maximum stroke ratios

Full size image

In the present results, most of the discharged flow entered the vortex ring and increased until \(T^{*} = 3.8\). The trailing vortex was captured behind the leading vortex ring at \(T^{*} = 14.5\), and the evolution of the vortex ring was observed. In addition, as \(T^{*}\) increases, smaller vortices are observed. The fact that the vortex ring was identified, and its evolution was simulated suggested that the CFD simulations were able to capture the relevant physical phenomena of the flow, further increasing the accuracy of the simulation results. Therefore, it can be considered that the simulations produced accurate and reliable results as the flow behavior and characteristics were in good agreement with previous literature results.

In this study, the propulsion performance evaluation index (PPEI, \({\upeta }\)) was introduced to quantitatively evaluate the propulsion performance of the VRT and the CoVoRT. The PPEI was defined as the ratio of the averaged kinetic energy in the flow direction generated in the entire domain and the kinetic energy of each jet for propulsion. The PPEI can be written as follows:

$$\eta = \frac{{\overline{E}_{kine} }}{{E_{jet} }} = \frac{{\frac{1}{2T}\rho \mathop \smallint \nolimits_{0}^{T} \int_{cv} {U_{x}^{2} d\forall } }}{{\frac{1}{2}m_{c} U_{C}^{2} + \frac{1}{2}m_{p} U_{p}^{2} }},$$
(4)

where \(E_{jet}\) is entrained energy by the primary jet and the Coanda jet, \(\overline{E}_{kine}\) is averaged kinetic energy in the direction of the piston motion over the whole computational domain. \(m_{c}\) and \(m_{p}\) are the mass of the flow discharged by the Coanda jet and the primary jet, respectively. \(U_{x}\) denotes the velocity component in the x-direction, \(U_{c}\) corresponds to the inflow velocity induced by the Coanda effect, and \(U_{p}\) represents the velocity of the primary jet.

The velocity ratio \((\lambda )\) of the primary jet to the Coanda jet was defined as:

$$\lambda = \frac{{U_{c} }}{{U_{p} }}.$$
(5)

Numerical simulations were performed to analyze the propulsion performance with two different the velocity ratios (\(\lambda = 0.5,{ }2.0)\). The computational domain is shown in Fig. 6, and the main particulars of the Coanda jet are presented in Table 6. The shape of the CoVoRT was designed following to the Coanda jet shape described by Rhee et al. [14].

Fig. 6
figure 6

Computational domain with Coanda jet

Full size image
Table 6 Main particulars of the CoVoRT
Full size table

Table 7 shows the PPEI of the VRT and the CoVoRT with the velocity ratios \((\lambda = 0.5,{ }2.0)\). The PPEI of the CoVoRT with \(\lambda = 0.5\) was increased by 45.3% compared to that of the VRT whereas in the case of \(\lambda = 2.0\), the PPEI was decreased by 9.3%.

Table 7 PPEI of the VRT and the CoVoRT with different velocity ratios
Full size table

To investigate the PPEI difference according to the change in velocity ratio, Fig. 7 presents the vorticity contours at \(t^{*} = 0.3\) and \(3.0\). At \(t^{*} = 0.3\), the CoVoRT with \(\lambda = 0.5\) showed a vorticity field similar to that of VRT.

Fig. 7
figure 7

Comparison of vorticity contours of VRT and CoVoRT with two different velocity ratio at t* = 3.0

Full size image

However, for the CoVoRT with \(\lambda = 2.0\), negative vorticity was formed around the piston exit due to the additional momentum flux by the Coanda jet. At \(t^{*} = 3.0\), the CoVoRT with \({\uplambda } = 0.5\) showed an increase in both the translation velocity and thickness of the trailing vortex ring, in comparison to the VRT, as a result of the Coanda jet’s continuous momentum addition to the background flow. On the other hand, for the CoVoRT with λ = 2.0, the large-scale leading vortex with positive and negative flowed into the entire domain, then the pinch-off phenomenon was occurred. It is due to the excessive momentum flux of the Coanda jet, and trailing vorticity was formed behind the leading vortex ring, adversely affecting propulsion performance. These results had been known to have a negative effect on propulsion performance, as the phenomenon of vortex ring separation mentioned by Krueger and Gharib (2003).

To quantitatively analyze the effect of negative vortex formation on the velocity distribution of the CoVoRT at the exit \(\left( {x/D_{p} = - 0.16} \right)\), Fig. 8 shows the velocity distribution of the VRT and the CoVoRT with \(\lambda = 0.5\) and 2.0 at \(t^{*} = 0.3\) and \(3.0\).

Fig. 8
figure 8

Exit velocity profile of VRT, CoVoRT with \(\lambda = 0.5\) and \(2.0\) at \(t^{*} = 0.3\) and \(3.0\)

Full size image

At the beginning of vortex ring formation \(\left( {t^{*} = 0.3} \right)\), the velocity at the center of the CoVoRT with \(\lambda = 0.5\) and 2.0 increased by 11.6% and 31.6%, respectively, compared to that of the VRT. At the end of the piston motion \(\left( {t^{*} = 3.0} \right)\), the velocity of the center of the CoVoRT with \(\lambda = 2.0\) slightly increased than that of the CoVoRT with \({\uplambda } = 0.5\). For the CoVoRT with \(\lambda = 2.0\), the velocity was increased in the range \(0.45 < y/D_{p} < 0.5\) due to the fluid ejection from the Coanda jet, and the maximum velocity was found at \(y/D_{p} = 0.45\). However, the negative vorticity caused the velocity to decrease rapidly in the rage of \(0.4 < y/D_{p} < 0.45\). In the end, the velocity at the center of the piston \(\left( {y/D_{p} = 0} \right)\) was similar regardless of the jet velocity ratio. In other words, the excessive momentum flux in the CoVoRT did not contribute to an increase in the velocity at the center of the piston, resulting in no improvement in propulsion performance. The reason for the PPEI difference between the VRT and the CoVoRT was identified from the dynamic characteristics of the vortex ring and the velocity distribution at the piston exit.

The exit height of the Coanda jet can also affect the PPEI of the VRT and the CoVoRT. Figure 9 presents the computational domain of the CoVoRT with different exit heights \(\left( {y_{c} /D_{p} = 0.05, 0.075, 0.1} \right)\) of the Coanda jet.

Fig. 9
figure 9

Computational domain of CoVoRT with different exit heights of the Coanda jet

Full size image

Table 8 shows the PPEI according to the change in the exit height of the Coanda jet, with a fixed velocity ratio of the primary jet and the Coanda jet at 0.5. In the case of \(y_{c} /D_{p} = 0.05\), the PPEI was improved by about 45%, while the PPEI generally decreased as the exit height increased.

Table 8 PPEI of the VRT and the CoVoRT with different exit heights of Coanda jet
Full size table

To elucidate the cause of the PPEI difference following the change in the height of the Coanda jet exit, Fig. 10 shows the contours of the vortex ring formation at \(t^{*} = 4.8\).

Fig. 10
figure 10

Vorticity contours with different exit height at \(t^{*} = 4.8\)

Full size image

In the case where \(y_{c} /D_{p} = 0.05\), the negative vortex did not significantly affect the velocity at the piston exit, allowing for a stable trailing jet. However, when the exit height of the Coanda jet increased, a negative vortex extended farther from the jet, resulting in the trailing jet separation and trailing vortex ring. These results suggest that the negative vortex generated by the Coanda jet entailed the PPEI difference.

Finally, the propulsion performance of the CoVoRT was investigated with respect to changes in the stroke ratio. The stroke ratio is defined as the ratio of the Coanda jet stroke \(\left( {T_{c}^{*} } \right)\) and the primary jet stroke \(\left( {T_{p}^{*} } \right)\), which can be written as follows

$$T_{c}^{*} = \frac{{L_{{m_{c} }} }}{{D_{p} }} = \frac{{U_{c} T}}{{D_{p} }},$$
(6)
$$T_{p}^{*} = \frac{{L_{{m_{p} }} }}{{D_{p} }} = \frac{{U_{p} T}}{{D_{p} }},$$
(7)

where \(L_{{m_{c} }}\) and \(L_{{m_{p} }}\) are the total moving distance of the piston in the Coanda jet and the primary jet, T represents the time the piston moves, and \(U_{c}\) and \(U_{p}\) are the Coanda jet velocity and the primary jet velocity, respectively.

To vary the stroke ratio, we adjusted \(U_{c}\) and \(U_{p}\) and evaluated the PPEI in two cases: (1) when the stroke ratio of the Coanda jet was the same as that of the primary jet, and (2) when it was different. First, the PPEI was analyzed at \(T_{c}^{*}\)=\(T_{p}^{*}\)=6, 8, and 10 for both the VRT and the CoVoRT with varying stroke ratios, and the results are presented in Table 9.

Table 9 PPEI of the VRT and the CoVoRT with the same stroke ratios
Full size table

Table 9 shows that the PPEI of the VRT and the CoVoRT decreased as the stroke ratio increased, which is consistent with experimental results reported by Bartol et al. [27]. To analyze the effect of changes in the stroke ratio on the PPEI, Fig. 11 shows the vortex ring at different stroke ratios for both the VRT and the CoVoRT at \(T_{p}^{*} = 6\) and 10.

Fig. 11
figure 11

Vorticity contours for VRT and CoVoRT with the same stroke ratios of Coanda and primary jets at t* = 4.8

Full size image

At \(T_{p}^{*} = 6\), the VRT showed the stable vortex ring formation. The CoVoRT also exhibited vortex ring formation similar to that of the VRT with an increased vortex ring velocity due to the additional momentum flux from the Coanda jet. However, at \(T_{p}^{*} = 10\), the onset of trailing vortex evolution was observed at \(x/D_{p} = 2.1\) for the VRT, and with the increase in the stroke ratio of the primary jet, the vortex ring formation became unstable. At \(T_{p}^{*} = T_{c}^{*} = 10\), the vortex ring of the CoVoRT separated from the trailing jet and developed a trailing vortex as a result of the excessive momentum flux from the Coanda jet. This phenomenon had a negative impact on the propulsion performance of the CoVoRT. The separation of the vortex rings and the formation of trailing vorticity are known to adversely affect the propulsion performance.

Next, the effect of different stroke ratios on the propulsion performance of the primary jet and the Coanda jet was investigated. CFD simulations were performed at a fixed \(T_{p}^{*}\) of 6, with three different stroke ratios of \(T_{c}^{*} = 6, 10\). Table 10 provides a comparison of the PPEI values between the CoVoRT and the VRT.

Table 10 PPEI of the VRT and the CoVoRT with different stroke ratios
Full size table

When the Coanda and primary jets moved with the same stroke ratios, the PPEI decreased as the stroke ratio of the Coanda jet increased. The largest increase rate of PPEI compared to the VRT was observed at \(T_{c}^{*} = 6\) (49.5%), while the smallest increase rate was at \(T_{c}^{*} = 10\) (17.9%). Figure 12 displays the vortex ring contours to identify the cause of the different PPEI values due to changes in the Coanda jet’s stroke ratio.

Fig. 12
figure 12

Vorticity contours for VRT and CoVoRT with different stroke ratios of Coanda and primary jets at \(t^{*} = 4.8\)

Full size image

At \(T_{p}^{*} = 6\) and \(T_{c}^{*} = 6\), the increase in vorticity was observed in both the trailing jet and vortex ring for the CoVoRT, as compared to the VRT. This increase in vorticity led to a rise in the averaged kinetic energy in the flow direction in the entire computational domain, resulting in an improvement in the PPEI.

However, at \(T_{p}^{*} = 6\) and \(T_{c}^{*} = 10\), the excessive momentum flux from the Coanda jet impeded the inflow of vorticity from the primary jet, leading to the “pinch-off” phenomenon. This resulted in the formation of trailing vorticity in the flow field. Based on the previous results, it was observed that when the stroke ratio of the Coanda jet was greater than that of the primary jet, the propulsion efficiency was reduced.

4 Summary and conclusion

In this study, a new vortex ring thruster utilizing the Coanda effect, named CoVoRT, was developed with the objective of improving the propulsion performance of the VRT, and its applicability was examined. To develop the CoVoRT, CFD simulations were conducted using the open-source CFD toolkit OpenFOAM, and for the purpose of result validation, comparisons were made with previous studies on the exit velocity distribution, total circulation, and vortex ring circulation, as well as the vortex ring formation process with changes in stroke ratio. The propulsion performance was evaluated based on the curvature radius of the Coanda wall, the velocity ratio of the Coanda jet and the primary jet, and the exit height of the Coanda jet.

In the first part of the study, the thrust performance was investigated for changes in the curvature radius of the Coanda wall. The results showed that as the curvature radius increased, the propulsion performance decreased compared to the case of the small curvature radius. This was due to the increased inflow angle, which prevented the entrainment of energy required to form the vortex ring.

The second part of the study examined the propulsion performance based on the changes in velocity ratio of the primary and Coanda jets. The PPEI of the CoVoRT with a velocity ratio of \(\lambda = 1.0\) was found to be improved by about 49.5% compared to that of the VRT. However, the PPEI of the CoVoRT with \(\lambda = 2.0\) decreased by about 9.3% compared to the VRT. As the velocity ratio increased, the excessive momentum flux from the Coanda jet led to the development of a separation of the vortex ring and trailing vorticity, which adversely affected the propulsion performance.

In the last part of the study, propulsion performance was examined based on the change in the exit height of the Coanda jet. When the exit height of the Coanda jet was set to \(y_{c} /D_{p} = 0.05\) and \(0.1\), the PPEI increased by approximately 45.3 and 34.7% compared to that of the VRT, respectively. The results showed that as the exit height increased, the effect of the negative vortex on the propulsion performance increased, resulting in the separation of the trailing jet and the formation of trailing vorticity. In cases where the exit height was large enough, negative vortices enhanced the separation of the trailing jet and trailing vorticity.

As a result, the newly developed CoVoRT, through changes in various design parameters, has demonstrated an improvement in propulsion performance compared to the VRT. It is anticipated that the vortex ring thruster developed in this study can be utilized in UUVs currently operating for various purposes.