1 Introduction

According to EMSA [1], ship navigational accidents attributed to collisions and groundings continue to dominate ship casualty statistics and lead to oil spills (Figs. 1, 2). Recent examples are the groundings of the bulk carrier MV Wakashio in Mauritius on 25 July 2020 (see Fig. 2) [2] and the Ro–Ro passenger ship Amorella in Finland on 20 September 2020 [3]. To mitigate risks, develop improved capability for force is investigations and new generation IMO SOLAS regulations it is useful to introduce practical, yet accurate methods for rapid assessment of ship grounding events.

Fig. 1
figure 1

Distribution of maritime casualty events over 2014–2019 [1]

Full size image
Fig. 2
figure 2

Wakashio grounding accident in Mauritius on 25 July 2020 [2]

Full size image

To date analytical methods for the estimation of grounding damage have been developed by Simonsen [4, 5], Sun et al. [6] and Zeng et al. [7]. Empirical formulas that may be used to obtain structural responses of ships in groundings have been presented by [8,9,10,11]. Recently, Pineau and Le Sourne [12] and Pineau et al. [13] introduced empirical formulas for the evaluation of ship structural response in hard groundings. In their model, rock mechanics are idealised by a paraboloid rock and grounding dynamics are idealised by the super-element method. The sensitivity of finite element (FE) methods has been studied by Glykas and Das [14], Zhang and Suzuki [15], Haris and Amdahl [16] and Nauyen et al. (2012).

The influence of hydrodynamic effects of the surrounding water has been studied by Le Sourne et al. [17, 18], Yu and Amdahl (2016) and Rudan et al. [19]. These methods demonstrated the importance of added on dynamic response. Recently, Kim et al. [20] confirmed the significance of evasive actions and hydrodynamic restoring forces on ship responses following collisions and groundings using large-scale LS-DYNA/MCOL. In a follow-up study, Conti et al. [21] introduced a comparative method scaling comparative collision damage distributions for use in probabilistic damage stability analysis. Due to the prohibitive cumulated computation time required by simulations considering the finite element method, in this work the collision scenarios were simulated using the super-element method (software programme SHARP).

FSI simulations using commercial algorithms are not open source. For example, the MCOL algorithm used in both SHARP super-element and LS-DYNA FE explicit solvers requires the input of hydrodynamic effects following the analysis of ship motions. This type of analysis is instilled with a broad number of computational modelling uncertainties and pertains to large-scale/uneconomic numerical computations. Also, with the exception of the work recently published by Kim et al. [20] FSI simulations mostly focus on collision dynamics only. This paper presents a simplified and general FSI method for the rapid analysis of ship grounding. Along the lines of earlier work presented by Kim et al. [22] the model utilizes a spring system to idealize mooring systems. Results are compared against the method of Kim et al. [20] for the case of a box-like vessel. Then, the validated method is applied for the case of a passenger ship.

2 Methodology

Global rigid ship dynamics can be idealized Newton’s equation of motion:

$$\left[ {M + M_{a} } \right]\left[ {\ddot{x}} \right] + \left[ G \right]\left[ {\dot{x}} \right] = \left[ {F_{R} \left( x \right)} \right] + \left[ {F_{D} \left( {\dot{x}} \right)} \right] + \left[ {F_{V} \left( {\dot{x}} \right)} \right] + \left[ {F_{C} } \right],$$
(1)

where \(\left[ x \right]\), \(\left[ {\dot{x}} \right]\) and \(\left[ {\ddot{x}} \right]\) represent the 6 degree of freedom (DoF) displacement, velocity and acceleration at the earth-fixed centre of gravity (CoG) of the ship, \(\left[ M \right]\) and \(\left[ {M_{a} } \right]\) are the structural mass/inertia and added mass/inertia matrices, \(\left[ G \right]\) is the skew-symmetrical gyroscopic matrix, and \(\left[ {F_{R} } \right]\), \(\left[ {F_{D} } \right]\), \(\left[ {F_{V} } \right]\) and \(\left[ {F_{C} } \right]\) are the hydrostatic restoring, wave damping, viscous and contact forces, respectively.

According to Kim et al. [20], hydrostatic restoring force and added mass are the most influential factors for ship structural response following groundings. The application of frequency-dependent wave damping forces is computationally demanding. This acknowledgement is fundamental with respect to the simplified FSI model presented.

2.1 Simplified idealization of the hydrostatic restoring forces

The hydrostatic restoring forces are defined as

$$\begin{aligned} & \left[ {F_{R} \left( x \right)} \right] = - \left[ K \right]\left[ x \right] \\ &\quad= - \rho g\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {A_{W} } & {A_{W} \cdot y_{W} } & { - A_{W} \cdot x_{W} } & 0 \\ 0 & 0 & {A_{W} \cdot y_{W} } & {J_{Wx} } & { - J_{Wxy} } & 0 \\ 0 & 0 & { - A_{W} \cdot x_{W} } & { - J_{Wxy} } & {J_{Wy} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {d_{x} } \\ {d_{y} } \\ {d_{z} } \\ {\theta_{x} } \\ {\theta_{y} } \\ {\theta_{z} } \\ \end{array} } \right], \end{aligned}$$
(2)

where \(\left[ K \right]\) is the hydrostatic restoring stiffness matrix, \(\left[ x \right]\) is the displacement matrix at CoG, \(\rho\) is the density of water, \(g\) is the gravitational acceleration, \(A_{W}\) is the area of waterplane, \(x_{W}\) and \(y_{W}\) are the location of CoG in each direction from the centre of waterplane, \(J_{Wx}\) and \(J_{Wy}\) are the second moment of inertia of waterplane area, and \(J_{Wxy}\) is the product of inertia, respectively.

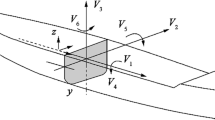
Let us assume that a ship is idealised as a rigid beam. FSI grounding contact dynamics on the ship’s heave axis of motion can be modelled by a spring that translates about the ship’s centre of gravity (CoG). Roll and pitch rotations in way of the centre of rotation (CoR) are idealised by a torsional spring (see Fig. 3). The distance between centers of gravity and rotation influence buoyancy (ship displacement) and in turn roll and pitch restoring forces.

Fig. 3
figure 3

Force and moments by restoring forces in the global system of ship

Full size image

The equilibrium equation of total forces and moments in way of the ship’s CoG are consequently defined as

$$\sum F_{{{\text{heave}}}} = F_{z} + \frac{{M_{x} }}{{y_{W} }} - \frac{{M_{y} }}{{x_{W} }} = - \rho g\left( {A_{W} d_{z} + A_{W} y_{W} \theta_{x} - A_{W} x_{W} \theta_{y} } \right),$$
(3a)
$$\because J_{Wx} = A_{W} y_{W}^{2} ,\quad J_{Wy} = A_{W} x_{W}^{2} ,$$
$$\sum M_{{{\text{roll}}}} = F_{z} y_{W} + M_{x} = M_{x} = - \rho g\left( {A_{W} y_{W} d_{z} + J_{Wx} \theta_{x} } \right),$$
(3b)
$$\sum M_{{{\text{pitch}}}} = - F_{z} x_{W} + M_{y} = - \rho g\left( { - A_{W} x_{W} d_{z} + J_{Wy} \theta_{y} } \right),$$
(3c)

where \({F}_{z}\), \({M}_{x}\) and \({M}_{y}\) are the heave, pitch and roll restoring forces in the global system of ship, \({F}_{\mathrm{heave}}\), \({M}_{\mathrm{pitch}}\) and \({M}_{\mathrm{roll}}\) are forces in the heave, pitch and roll directions at CoG, respectively.

Under conditions of symmetry (\({J}_{Wxy}=0\)). Thus, the total restoring force can be defined as:

$$\left[ {F_{{R_{{{\text{spring}}}} }} \left( x \right)} \right] = - \left[ K \right]\left[ x \right] = - \rho g\left[ {\begin{array}{*{20}c} {A_{W} } & {A_{W} y_{W} } & { - A_{W} \cdot x_{W} } \\ {A_{W} y_{W} } & {J_{Wx} } & 0 \\ { - A_{W} \cdot x_{W} } & 0 & {J_{Wy} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {d_{z} } \\ {\theta_{x} } \\ {\theta_{y} } \\ \end{array} } \right].$$
(4)

\([{F}_{{R}_{\mathrm{spring}}}\left(x\right)]\) is the restoring force matrix by spring elements in the FE model.

This concludes that a translational spring of stiffness \({F}_{z}/{d}_{z}=\rho g{A}_{W}\) (unit: force/displacement) for heave, and torsional springs with \({M}_{x}/{\theta }_{x}=\rho g{J}_{Wx}\) and \({M}_{y}/{\theta }_{y}=\rho g{J}_{Wy}\) (unit: moment/angle) for roll and pitch directions can be applied on an FEA idealisation so as to idealise the influence of hydrostatic restoring forces (see Fig. 3).

2.2 Simplified idealization of the added mass

The added mass of a fluid can be expressed in 6-DOF by the matrix as Eq. 5.

$$\left[{M}_{a}\right]=\left[\begin{array}{cccccc}{m}_{11}& 0& {m}_{13}& 0& {m}_{15}& 0\\ 0& {m}_{22}& 0& {m}_{24}& 0& {m}_{26}\\ {m}_{31}& 0& {m}_{33}& 0& {m}_{35}& 0\\ 0& {m}_{42}& 0& {m}_{44}& 0& {m}_{46}\\ {m}_{51}& 0& {m}_{53}& 0& {m}_{55}& 0\\ 0& {m}_{62}& 0& {m}_{64}& 0& {m}_{66}\end{array}\right],$$
(5)

where \({m}_{ij}\) is an added mass in the ith-direction caused by an acceleration in jth-direction assuming port/starboard symmetry [23]. This model can be applied to the ship’s CoG during seakeeping analysis [23, 24]. For the model presented in this paper, the hydrodynamic effects from the added mass matrix obtained using Hydrostar [25] are distributed on FEA nodes in way of the CoG of the structure. It is noted that it may be possible to apply the added masses by empirical formulae [26,27,28,29,30].

3 Validation with existing method

MCOL is a subroutine program in LS-DYNA that accounts for hydrodynamic properties in structural response analysis. MCOL is well known and validated solver (see [Le Sourne et al. 2021, 17–19, 31, 37], [38], [39]), the LS-DYNA with MCOL explicit FE code was adopted to validate the simplified FSI model using spring elements. This idealisation accounts for the influence of ship positions at each time step [17, 32] via inclusion of the following parameters in 6 DoF:

  • Mass matrix of target structure (both structural mass and cargo load)

  • Hydrostatic restoring forces and moments

  • Added mass matrix

The comparisons presented in this paper did not account for velocity-dependent viscous damping and ship’s frequency-dependent wave damping forces. This is because such forces do not significantly affect the structural behavior [20] and it is difficult to model them by pure FE analysis without the use of a subroutine program.

3.1 FSI idealization of a barge structure

The general particulars, topology, and properties of the barge used to validate the simplified FSI model are given in Tables 1 and 2, and Fig. 4.

Table 1 Principal dimensions and structural details of the box-shaped ship
Full size table
Table 2 Material properties applied to the box-shaped ship in the present study
Full size table
Fig. 4
figure 4

Structural layout (left) and midship (right) of the box-shaped ship. (NB: The distance between

Full size image

Equations 6 and 7 show the mass matrix (mass and mass moment of inertia) and restoring stiffness matrix for a box-shaped ship.

$$\left[{M}_{\mathrm{box}}\right]=\left[\begin{array}{cccccc}11469& 0& 0& 0& 0& 0\\ 0& 11469& 0& 0& 0& 0\\ 0& 0& 11469& 0& 0& 0\\ 0& 0& 0& 5.752\times {10}^{5}& 0& 0\\ 0& 0& 0& 0& 1.010\times {10}^{7}& 0\\ 0& 0& 0& 0& 0& 1.030\times {10}^{7}\end{array}\right],$$
(6)
$$\left[{K}_{\mathrm{box}}\right]=\left[\begin{array}{ccc}1.609\times {10}^{7}& 0& 0\\ 0& 3.432\times {10}^{8}& 0\\ 0& 0& 1.341\times {10}^{10}\end{array}\right],$$
(7)

where, \([{M}_{\mathrm{box}}]\) and \([{K}_{\mathrm{box}}]\) are the mass and restoring stiffness matrices for the box-shaped ship, respectively. Units are defined as: ton (for mass), ton·m2 (for mass moment of inertia), N/m (for heave stiffness), N m (for roll and pitch stiffnesses), and N (for the bi-products of stiffnesses).

The FEA model comprised of shell elements based on the Belytschko-Tsay formulation that accounts for the translational and rotational velocity of nodes in 6 DoF [33]. And 150 \(\times\) 150 (mm) size of elements obtained by the mesh convergence study [20] at the impact zone (until 3 m above the bottom) is applied.

Strain-rate (dynamic) effects were idealized according to the Cowper-Symonds equation [34, 35]:

$${\sigma }_{Yd}=\left[1+{\left(\frac{\dot{\varepsilon }}{C}\right)}^{1/q}\right]{\sigma }_{Y},$$
(8)

where \({\sigma }_{Yd}\) and \({\sigma }_{Y}\) are the yield strength in static and dynamic loads, \(\dot{\varepsilon }\) is the strain rate, and \(C\) and \(q\) are material related (Cowper–Symonds) coefficients.

Kim et al. [20] defined various grounding accidental scenarios for passenger ships according to [36] criteria. Based on this work the typical forward vessel speed of 11 knots, the rock shapes and grounding location shown in Figs. 5 and 6 were considered representative enough for the simplified case considered.

Fig. 5
figure 5

Definition of rock’s shape and dimensions

Full size image
Fig. 6
figure 6

Grounding scenarios for developing FE technique

Full size image

Since the centre of waterplane area in x and y directions coincides with the barge CoG, both translational and torsional springs were located in way of the CoG (see Fig. 4). To apply spring elements in the FE analysis, it is necessary to use additional nodes in way of spring ends. This modelling approach ensures that spring elements will not be affected by the stiffness of any structural element. Additional nodes placed close to the CoG help ensure the influence of heave, roll and pitch motions (see Fig. 7). Table 3 presents the body fixed boundary condition at each additional node, and the corresponding constraint conditions.

Fig. 7
figure 7

Location of additional nodes for applying spring elements

Full size image
Table 3 Boundary and constraint conditions at additional nodes
Full size table

Figures 8, 9, 10 and 11 demonstrate comparison of results between the simplified FSI method and the large-scale LS-DYNA/MCOL model. Comparison of the roll angles is not presented for scenarios 1 and 2 (see Fig. 6) as they are negligible for the case of centreline grounding. In general, it seems that the simplified model with spring elements depicts well the effects of hydrostatic restoring forces and added mass. However, it gives longer surge displacement. This could be attributed to differences in motion predictions when using the deformable spring element of the method developed against the rigid MCOL simulations.

Fig. 8
figure 8

Comparison of ship motions of box-shaped ship in scenario 1

Full size image
Fig. 9
figure 9

Comparison of ship motions of box-shaped ship in scenario 2

Full size image
Fig. 10
figure 10

Comparison of ship motions of box-shaped ship in scenario 3

Full size image
Fig. 11
figure 11

Comparison of ship motions of box-shaped ship in scenario 4

Full size image

In scenario 3 corresponding to side groundings with Rock I (see Fig. 10), there are bigger differences in roll angle (Fig. 10a, b). These differences do not affect the damage length as the barge stops very soon after the grounding initiation. From an overall perspective, the influence of added mass appears to be minor. Added mass leads to smaller surge displacement possibly because of the additional kinetic energy dissipation effects.

3.2 FSI idealization of a full-scaled ship

The Ro–Ro passenger ship of Fig. 12 and Tables 2 and 4 was used for full scale hard grounding simulations at 11 knots forward speed.

Fig. 12
figure 12

Target ship for the application of developed model

Full size image

Equations 9 and 10 present, respectively, the mass matrix (including the influence of mass and mass moment of inertia) and restoring stiffness matrix for the passenger ship. The barge presented in Sect. 3.1 has a constant water plane area. Arguably, the water plane area of a real ship depends on draught variations and may vary along the ships’s depth. It is acknowledged that this may lead to variable restoring forces. However, in this study, the changes of water plane area were assumed small and, therefore, constant restoring stiffnesses may be considered acceptable.

$$\left[ {M_{{{\text{ship}}}} } \right] = \left[ {\begin{array}{*{20}c} {33879} & 0 & 0 & 0 & 0 & 0 \\ 0 & {33879} & 0 & 0 & 0 & 0 \\ 0 & 0 & {33879} & 0 & 0 & 0 \\ 0 & 0 & 0 & {6.669 \times 10^{6} } & 0 & {2.335 \times 10^{6} } \\ 0 & 0 & 0 & 0 & {9.760 \times 10^{7} } & 0 \\ 0 & 0 & 0 & {2.335 \times 10^{6} } & 0 & {9.760 \times 10^{7} } \\ \end{array} } \right],$$
(9)
$$\left[ {K_{{{\text{ship}}}} } \right] = \left[ {\begin{array}{*{20}c} {5.836 \times 10^{7} } & 0 & {1.573 \times 10^{8} } \\ 0 & {8.569 \times 10^{8} } & 0 \\ {1.573 \times 10^{8} } & 0 & {1.770 \times 10^{11} } \\ \end{array} } \right],$$
(10)

where \([{M}_{\mathrm{ship}}]\) and \([{K}_{\mathrm{ship}}]\) are the mass and restoring stiffness matrices for the passenger ship, respectively. Units are same with Eqs. 6 and 7.

In contrast with the barge model, for the case of the real ship CoG and CoR did not coincide in length and depth directions. Accordingly the heave spring was applied at CoG, and pitch and roll springs were located at CoR for considering the restoring forces (see Fig. 13). Additional nodes in way of spring ends were located as described in Fig. 7. The applied structural boundary/constraint conditions are presented in Table 4. An additional mass node was employed to apply the 6 \(\times\) 6 added mass at CoG.

Fig. 13
figure 13

Applied spring elements for restoring forces in the real ship

Full size image
Table 4 Principle dimensions of the target passenger ship
Full size table

Figures 14, 15, 16 and 17 demonstrate motions and structural responses. Spring elements and additional mass nodes appear to describe well the hydrostatic restoring forces and added masses. However, for side grounding (B/4 from the centreline) with Rock I (scenario 3) which has broader contact area than Rock II, there is a small difference of ship motions in heave, pitch and roll. In scenario 3, when the new method is implemented, the heave motion and period reach their maximum before MCOL simulations. This could be attributed to the loss of structural members during simplified FSI method as opposed to the LS-DYNA/MCOL model assumes constant mass/moment of inertia (pure rigid body dynamics) throughout the simulation.

Fig. 14
figure 14

Ship motions and structural response of the target ship in scenario 1

Full size image
Fig. 15
figure 15

Ship motions and structural response of the target ship in scenario 2

Full size image
Fig. 16
figure 16

Ship motions and structural response of the target ship in scenario 3

Full size image
Fig. 17
figure 17

Ship motions and structural response of the target ship in scenario 4

Full size image

Similarly to the box-shaped ship simulations, the method slightly overestimates surge displacement (grounding length) and internal energy. This could relate to the evaluation of ship motions. The simplified method concurrently calculates motions (displacement) and structural mechanics at each time step, while LS-DYNA and MCOL counter-map reaction forces/moments at each time step (see Fig. 18).

Fig. 18
figure 18

Scheme of motion and structural analysis by simplified and existing methods

Full size image

4 Conclusions

This paper presented a simplified FSI method that accounts for the influence of surrounding water (i.e., restoring force and 6 DoF added mass) during ship grounding dynamics. Heave, pitch and roll hydrodynamic forces are idealised by spring elements and additional mass nodes. The translational spring is used to substitute the heave restoring stiffness, and torsional springs are used to simulate pitch and roll restoring stiffnesses. The additional mass node accounts for added mass effects in 6 DoF. Key conclusions follow:

  • The simplified FSI method describes well hydrodynamic properties. This is justified by the fact that structural crashworthiness obtained by the developed approach is in good agreement with results obtained by the LS-DYNA/MCOL idealization.

  • The new method overestimates marginally the grounding length (surge displacement) and internal energy. This could be attributed to different assumptions in the evaluation of ship motions (e.g., deformable body assumption in the simplified FSI method versus rigid body dynamics in LS-DYNA/MCOL model).

  • The method presented could be useful for rapid assessment of grounding. It can also be extended to idealize ship collision analysis dynamics by applying spring elements on both striking and struck ships.  Such capabilities may be useful for ship damage stability assessment using direct [40] and comparative analysis methods [41].