Time-domain TEBEM method for wave added resistance of ships with forward speed

Abstract

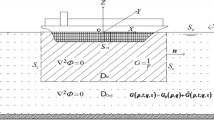
A numerical method for solving 3D unsteady potential flow problem of ship advancing in waves was put forward. The flow field was divided into an inner and an outer domain by introducing an artificial matching surface. The inner domain was surrounded by a ship-wetted surface and a matching surface as well as part of the free surface. The free-surface condition for the inner domain was formulated by perturbation about the double-body (DB) flow assumption. The outer domain was surrounded by a matching surface and the rest had a free surface as well as an infinite far-field radiation boundary. The free-surface condition for the outer domain was formulated by perturbation of the uniform incoming flow. The simple Green function and transient free-surface Green function were used to form the boundary integral equation (BIE) for the inner and outer domains, respectively. The Taylor expansion boundary element method (TEBEM) was adopted to solve the DB flow and inner-domain and outer-domain unsteady flow BIE. Matching conditions for the inner-domain flow and outer-domain flow were enforced by the continuity of velocity potential and normal velocity on the matching surface. Direct pressure integration on the ship-wetted surface was applied to obtain the first- and second-order wave forces. The numerical prediction on the displacement, acceleration and added resistance of the 14000-TEU container ship at different forward speeds were investigated by the proposed TEBEM method. Reynolds-Averaged Navier–Stokes (RANS) equations based on Computational Fluid Dynamics (CFD) method were adopted to compare with TEBEM method. The physical tank experiment results also validated the accuracy of the numerical tank results. Compared with the experimental solutions, TEBEM obtained good agreement with the RANS CFD method. TEBEM, however, was much more efficient and robust.

Appendix

According to the Gauss’ theorem, the hydrostatic pressure integration provides no contribution to the added resistance of ships. The detailed derivation process is shown as following.

We can get the hydrostatic pressure integral term from Eq. (10), as following:

$$ - \rho \iint\limits_{{S_{{\text{H}}} }} {gz\vec{n}^{(2)} {\text{d}}s}, $$

(24)

where $\vec{n}^{(2)} = H^{(2)} \vec{n},\quad \vec{n} = \left( {n_{1}^{\left( 0 \right)} ,n_{2}^{\left( 0 \right)} ,n_{3}^{\left( 0 \right)} } \right)^{{\text{T}}}$, $H^{(2)} = - \frac{1}{2}\left[ {\begin{array}{*{20}c} {\eta_{5}^{2} + \eta_{6}^{2} } & { - 2\eta_{4} \eta_{5} } & { - 2\eta_{4} \eta_{6} } \\ 0 & {\eta_{4}^{2} + \eta_{6}^{2} } & { - 2\eta_{5} \eta_{6} } \\ 0 & 0 & {\eta_{4}^{2} + \eta_{5}^{2} } \\ \end{array} } \right]$.

For the added resistance, we pay attention to the integration contribution of Eq. (24) in x axis direction:

$$ \begin{aligned} F_{{{\text{SX}}}}^{\left( 2 \right)} & = - \rho \iint\limits_{{S_{{\text{H}}} }} {gzn_{1}^{\left( 2 \right)} {\text{d}}s} = - \rho \iint\limits_{{S_{{\text{H}}} }} {gz\left( { - \frac{1}{2}\left( {\eta_{5}^{2} + \eta_{6}^{2} } \right)n_{1}^{\left( 0 \right)} + \eta_{4} \eta_{5} n_{2}^{\left( 0 \right)} + \eta_{4} \eta_{6} n_{3}^{\left( 0 \right)} } \right){\text{d}}s} \\ & \quad = \frac{1}{2}\left( {\eta_{5}^{2} + \eta_{6}^{2} } \right)\rho g\iint\limits_{{S_{{\text{H}}} }} {zn_{1}^{\left( 0 \right)} {\text{d}}s} - \eta_{4} \eta_{5} \rho g\iint\limits_{{S_{{\text{H}}} }} {zn_{2}^{\left( 0 \right)} {\text{d}}s} - \eta_{4} \eta_{6} \rho g\iint\limits_{{S_{{\text{H}}} }} {zn_{3}^{\left( 0 \right)} {\text{d}}s}. \\ \end{aligned} $$

(25)

According to Gauss’ theorem, the following integration results can be obtained easily

$$ \iint\limits_{{S_{{\text{H}}} }} {zn_{1}^{\left( 0 \right)} {\text{d}}s} = 0;\quad \iint\limits_{{S_{{\text{H}}} }} {zn_{2}^{\left( 0 \right)} {\text{d}}s} = 0;\quad \iint\limits_{{S_{{\text{H}}} }} {zn_{3}^{\left( 0 \right)} {\text{d}}s} = \forall . $$

Thus, we can get Eq. (26)

$$ F_{{{\text{SX}}}}^{\left( 2 \right)} = - \rho \iint\limits_{{S_{{\text{H}}} }} {gzn_{1}^{\left( 2 \right)} {\text{d}}s} = - \eta_{4} \eta_{6} \rho g\forall . $$

(26)

$- \rho \iint\limits_{{S_{H} }} {g\delta_{3} }\vec{n}^{(1)} ds$ is also involved in Eq. (10), where $\delta_{3}$ means the vertical displacement of ships

$$ \delta_{3} = \eta_{3} + \eta_{4} y - \eta_{5} x,\quad \vec{n}^{(1)} = H^{(1)} \vec{n},\quad \vec{n} = \left( {n_{1}^{\left( 0 \right)} ,n_{2}^{\left( 0 \right)} ,n_{3}^{\left( 0 \right)} } \right)^{T} ,\quad H^{(1)} = \left[ {\begin{array}{*{20}c} 0 & { - \eta_{6} } & {\eta_{5} } \\ {\eta_{6} } & 0 & { - \eta_{4} } \\ { - \eta_{5} } & {\eta_{4} } & 0 \\ \end{array} } \right]. $$

Similarly, we also pay attention to the integration contribution in x axis direction

$$ \begin{aligned} F_{{{\text{MX}}}}^{(2)} & = - \rho \iint\limits_{{S_{{\text{H}}} }} {g\left( {\eta_{3} + \eta_{4} y - \eta_{5} x} \right)\left( { - \eta_{6} n_{2}^{\left( 0 \right)} + \eta_{5} n_{3}^{\left( 0 \right)} } \right){\text{d}}s} \\ & \quad = - \rho g\iint\limits_{{S_{{\text{H}}} }} {\left( { - \eta_{3} \eta_{6} n_{2}^{\left( 0 \right)} + \eta_{3} \eta_{5} n_{3}^{\left( 0 \right)} - \eta_{4} \eta_{6} yn_{2}^{\left( 0 \right)} + \eta_{4} \eta_{5} yn_{3}^{\left( 0 \right)} + \eta_{5} \eta_{6} xn_{2}^{\left( 0 \right)} - \eta_{5}^{2} xn_{3}^{\left( 0 \right)} } \right)}{\text{d}}s. \\ \end{aligned} $$

(27)

From Gauss’ theorem, these integral contribution can also be got easily

$$ \begin{aligned} & \iint\limits_{{S_{{\text{H}}} }} {n_{1}^{\left( 0 \right)} {\text{d}}s} = 0;\quad \iint\limits_{{S_{H} }} {n_{2}^{\left( 0 \right)} {\text{d}}s} = 0;\quad \iint\limits_{{S_{{\text{H}}} }} {n_{3}^{\left( 0 \right)} {\text{d}}s} = A_{{\text{w}}} ; \\ & \iint\limits_{{S_{{\text{H}}} }} {yn_{2}^{\left( 0 \right)} {\text{d}}s} = \forall ;\quad \iint\limits_{{S_{{\text{H}}} }} {yn_{3}^{\left( 0 \right)} {\text{d}}s} = y_{{\text{f}}} \cdot A_{{\text{w}}} ;\quad \iint\limits_{{S_{{\text{H}}} }} {xn_{2}^{\left( 0 \right)} {\text{d}}s} = 0;\quad \iint\limits_{{S_{{\text{H}}} }} {xn_{3}^{\left( 0 \right)} {\text{d}}s} = x_{{\text{f}}} \cdot A_{{\text{w}}} , \\ \end{aligned} $$

where $x_{f}$ and $y_{f}$ mean the x- and y-coordinate of the center of the waterplane. Usually, the ship is symmetrical about the middle line plane, hence $y_{{\text{f}}} = 0$.

Consequently, we can get the integral contribution of Eq. (27)

$$ F_{{{\text{MX}}}}^{(2)} = \left( { - \rho g\eta_{3} \eta_{5} A_{{\text{w}}} + \rho g\eta_{4} \eta_{6} \forall + \rho g\eta_{5}^{2} x_{{\text{f}}} A_{{\text{w}}} } \right). $$

(28)

Obviously, the integral contribution of hydrostatic pressure in the x axis direction can be omitted, if the comparison is made between Eqs. (26) and (28). Namely, the total integral contribution of Eqs. (26) and (28) for the added resistance of ships is following:

$$ F_{{{\text{SX}}}}^{(2)} + F_{{{\text{MX}}}}^{(2)} = \left( { - \rho g\eta_{3} \eta_{5} A_{{\text{w}}} + \rho g\eta_{5}^{2} x_{{\text{f}}} A_{{\text{w}}} } \right). $$

(29)

The same analysis process is used to the integral contribution in the y axis direction and z axis direction. So, in the y axis direction

$$ \begin{aligned} & F_{{{\text{SY}}}}^{(2)} = - \rho \iint\limits_{{S_{{\text{H}}} }} {gzn_{2}^{\left( 2 \right)} {\text{d}}s} = - \eta_{5} \eta_{6} \rho g\forall , \\ & F_{{{\text{MY}}}}^{(2)} = - \rho \iint\limits_{{S_{{\text{H}}} }} {g\left( {\eta_{3} + \eta_{4} y - \eta_{5} x} \right)\left( {\eta_{6} n_{1}^{\left( 0 \right)} - \eta_{4} n_{3}^{\left( 0 \right)} } \right){\text{d}}s} = \left( {\rho g\eta_{3} \eta_{4} A_{{\text{w}}} + \rho g\eta_{5} \eta_{6} \forall - \rho g\eta_{4} \eta_{5} x_{{\text{f}}} A_{{\text{w}}} } \right), \\ & F_{{{\text{SY}}}}^{(2)} + F_{{{\text{MY}}}}^{(2)} = \left( {\rho g\eta_{3} \eta_{4} A_{{\text{w}}} - \rho g\eta_{4} \eta_{5} x_{{\text{f}}} A_{{\text{w}}} } \right). \\ \end{aligned} $$

(30)

In the z-axis direction

$$ \begin{aligned} & F_{{{\text{SZ}}}}^{\left( 2 \right)} = - \rho \iint\limits_{{S_{{\text{H}}} }} {gzn_{3}^{\left( 2 \right)} {\text{d}}s} = \frac{1}{2}\left( {\eta_{4}^{2} + \eta_{5}^{2} } \right)\rho g\forall , \\ & F_{{{\text{MZ}}}}^{\left( 2 \right)} = - \rho \iint\limits_{{S_{{\text{H}}} }} {g\left( {\eta_{3} + \eta_{4} y - \eta_{5} x} \right)\left( { - \eta_{5} n_{1}^{\left( 0 \right)} + \eta_{4} n_{2}^{\left( 0 \right)} } \right)}\\&{ {\text{d}}s} = \left( { - \rho g\eta_{4}^{2} \forall - \rho g\eta_{5}^{2} \forall } \right), \\ & F_{{{\text{SZ}}}}^{\left( 2 \right)} + F_{{{\text{MZ}}}}^{\left( 2 \right)} = - \frac{1}{2}\left( {\eta_{4}^{2} + \eta_{5}^{2} } \right)\rho g\forall . \\ \end{aligned} $$

(31)

Therefore, from Eqs. (29–31), we can say that the hydrostatic pressure only acts in the vertical direction for a general-shape floating body, which is consistent with Gauss’ theorem.