1 Introduction

Everybody is aware of the danger of a ship sailing in rough seas. The risk significantly increases for small and fast vessels, since they are more exposed to relatively large motions. The integrity of those ships and the safety of the crew are compromised by the action of the waves on the hull, which can result in lower transverse stability, high accelerations, and course keeping problems. The seakeeping of these ships is widely studied in head and bow quartering sea conditions, since the accelerations in the vertical plane are often a limiting factor for the vessel operability. However, several past studies [1,2,3,4,5,6,7,8,9,10,11,12,13] focused on the problem of a vessel sailing in following and stern-quartering waves, recognizing it as a dangerous situation for a ship at sea. In these conditions, the large wave-induced yawing moment turns the ship from its original course despite any steering counter-actions. The danger is also recognized by mariners, who are particularly concerned by the difficulty of course keeping and the associated potential hazards such broaching-to and capsizing.

The dynamic instability of ships sailing in following seas is extremely complex and the causes governing this type of phenomena are not yet well understood. In most cases, the vessel is captured by the incoming stern wave and accelerated to its speed (surf-riding); then, the vessel is suddenly turned beam on to the seaway, phenomenon known as broaching-to. In extreme cases, these events are quick and violent, and can lead to a capsize. Surf-riding and broaching-to are strictly connected phenomena. Usually broaching-to is preceded by surf-riding. These phenomena can be studied in a quasi-steady fashion [1], since the relative encounter frequency between the waves and the ship is very low during a surf. The vessel is “frozen” on a certain wave position, and the hull loads are related to that location on the wave.

The ship dynamics in following waves results from a combination of the seakeeping and manoeuvrability characteristics of the vessel. Hull hydrodynamic and hydrostatic loads, steering forces, and wave destabilizing effect contribute to different extents to the onset of loss of control. Manoeuvring loads on the hull are largely dependent on the wave characteristics and in the relative position that the vessel assumes on a wave. Variations of the hull submerged geometry result in great differences in the loads acting on the ship. These variations are particularly significant on small craft: the waves are relatively large with respect to the hull size. These loads must be predicted as a function of the longitudinal position in the wave and considering the correct hull submerged geometry at that position.

Ship manoeuvrability studies have usually been confined to the three degrees of freedom in the horizontal plane: surge, sway, and yaw. Roll is often neglected in manoeuvrability research [14]. In other works [15,16,17,18,19,20,21,22], the effect of roll on manoeuvrability was considered, mainly in calm water, both for displacement and semi-displacement vessels. Roll can affect the manoeuvrability of small craft in waves, since the heel angle significantly changes the submerged hull characteristics. When heeled, the vessel experiences a side force and a yawing moment due to the non-symmetric submerged geometry. In the literature, these effects are denominated as heel–yaw and heel–sway coupling [18] or as heel-induced loads [23]. Hereby, both the expression will be used in an equivalent way. Because of the already great complexity of the problem, the effect of the heel–sway and heel–yaw hydrodynamic coupling in following waves is not commonly investigated, either experimentally or numerically. This paper presents an investigation of the coupling between heel and the manoeuvring loads in following waves by means of experimental captive model tests. The experiments are a starting point in the understanding of this physical problem and its characterization by numerical tools.

In an earlier work by Hashimoto et al. [23], captive model tests were carried out in following waves to determine the heel-induced loads on a fishing vessel, for one wave condition and one speed. That study considered high heel angles to realize quantitative prediction of the capsize dynamics due to broaching-to. In the current work, the heel-induced loads on a high-speed craft are investigated experimentally, but at a lower range of heel angles. The interest is directed to the linear characterization of the manoeuvring loads and the inception of dynamic instabilities. Furthermore, hard-chine craft in these sea conditions usually experiences moderate roll angles which are often between 10° and 15°.

In the experimental set-up in [23], the vertical position of the ship model was fixed during each run, and then, the coefficients were corrected to account for the error in the ship heave and pitch position on the wave. In the current study, the experimental set-up was different. The ship model was fully constrained by a 6DOF oscillator (Hexapod), which moved in heave and pitch to achieve the vertical equilibrium of forces and moments of the model in the wave. This was meant to reproduce the most natural vertical attitude of the craft in waves, since the manoeuvrability of the vessel is affected by the ship position in the water. The oscillations were calculated beforehand and used as the main input to the Hexapod.

Fully constraining the model to an oscillator ensures a better stiffness of the experimental set-up: a set-up moving in heave and pitch and fixed in the other motions might interfere with the measurement of the loads in an unpredictable manner. Furthermore, the use of an oscillator allows the model to be orientated in every desired direction making it possible to measure the sensitivity of the loads with respect to well-defined positions of the model. This is very meaningful for manoeuvring and seakeeping applications: it is possible to measure all the forces and moments acting on the model in waves in static conditions or with forced oscillations [24]. In this work, the model was forced to assume its equilibrium position on the wave; more in general, the model can be forced to assume every prescribed position or to perform every oscillation on the waves.

Given the high complexity of the problem, the numerical determination of the manoeuvring loads on a heeled ship is difficult. High-speed craft are commonly assumed to be symmetrical for the purpose of validation of the calculation of the hydrodynamic pressure distribution, devoting attention to the dynamics in the vertical plane [25, 26]. Non-symmetric hard-chine heeled hulls have been studied numerically by several past researchers [27,28,29], mainly in calm water or head waves, by means of strip theory codes or simplified 2D BEM. The production of lift in heeled conditions is governed by very complex viscous phenomena (such as the separation of the flow at the chine), which are difficult to predict with slender body theories or potential flow models. Often, the results given by these numerical tools are not satisfactory, and do not focus on the effect of heel on the manoeuvring characteristics of the vessel. A validation of more sophisticated numerical fluid solvers for these conditions is still lacking.

In this work, the experimental data collected were used to define an empirical description of the loads in the domain of ship speeds and wavelengths. The aim is to be able to predict these loads over the widest interesting range of ship speeds and wavelengths. This empirical description of heel-induced loads was used to correct a 3D blended potential flow BEM with the final objective of understanding the effect of the heel-induced loads in the inception of dynamic instabilities.

In [18], Renilson and Manwarring used the heel–yaw and heel–sway coupling loads obtained experimentally in calm water to assess their effect on the inception of broaching-to. The outcomes showed that the heel-induced loads increase the likelihood of broaching-to. After the experimental investigation in following waves already mentioned in this introduction, Hashimoto et al. [23] proved that the heel-induced loads have the consequence of stabilizing the ship contrarily to what found in [18]. In the present study, this phenomenon was investigated extending the investigation in [23] to a higher number of wave and vessel speed conditions.

2 The captive model tests

2.1 Test case definition

The experimental campaign covered six different following wave conditions, resulting from a combination of three ship velocities and five waves. The velocities and the wavelengths were chosen to cover a large region where a course dynamic instability event could occur, within a reasonable number of tests to be performed. Since the loss of directional control usually happens when the ship speed is accelerated approximately to the wave celerity, the following wave crests were chosen to overtake the model at low encounter frequency. The wave slope, H/λ, was 0.06 (about 1/16) in all the conditions tested. The choice of the steepness was dictated by the limitation of the wave-making process in the towing tank. Although the dynamic course stability events could happen at higher steepness, 0.06 was the upper limit to guarantee a good quality of the waves, avoiding breaking. Each case was repeated at different heel angles, to determine the effect of heel angle on the force and moment in different positions in the wave. The conditions are summarized in Table 1 and visually depicted in Fig. 1.

Table 1 Particulars of the six conditions tested during the experiments in terms of model speed, wavelength, and wave encounter frequency
Full size table
Fig. 1
figure 1

Experimental test cases. Above the line, the wave celerity is greater than ship speed (following waves); the measurement conditions were chosen in the speed–wavelength region where broaching-to is more likely to occur (H/λ = 0.06, μ = 0 deg)

Full size image

The experimental campaign was executed using a model of the rescue boat SAR NH-1816 of the Royal Netherlands Sea Rescue Institution (KNRM). The hull lines are shown in Fig. 2. The ship main dimensions and characteristics are freely available at www.KNRM.nl, and reported in Table 2. The vessel design originates from the axe-bow concept [30] applied, for the first time, to a small high-speed craft. The axe-bow improves the seakeeping characteristics of the vessel in head sea [31]. Still more studies on the manoeuvring characteristics of this type of vessels [8] are needed to fully assess the manoeuvring behaviour of fast small vessels and the influence of the axe-bow.

Fig. 2
figure 2

Hull lines of the SAR-NH1816 rescue vessel

Full size image
Table 2 Main characteristic of the rescue boat NH-1816
Full size table

2.2 Experimental procedure

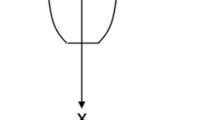
During the captive model tests, all the forces, moments, and motions were measured in 6 degrees of freedom (DOF). Hereby, the attention will be devoted to the total hydrodynamic loads in sway, Y′, and yaw, N′, of the high-speed craft at a heel angle in following waves. This is to focus on the effect of heel onto the manoeuvring characteristic of the vessel. Forces, moments, translations, and rotations are referred to the centre of the coordinate system shown in Fig. 3, located at G.

Fig. 3
figure 3

Coordinate systems. The origin of the ship moving frame is in the ship centre of gravity G; the axes x and y lie on the horizontal plane, while z is constantly vertical and pointing downwards. The location of the vessel in the wave is denoted by the distance of G from the nearest approaching following wave’s crest, ξG

Full size image

The experiments were conducted in a rectilinear towing tank, the wave incidence angle, μ, and the drift angle, β, being zero during the entire experimental campaign. Thus, sway force, Y′, and yaw moment, N′, acting on the horizontal plane were caused exclusively by the ship heel angle. The loads depend on the longitudinal location of the ship centre of gravity on the wave, ξG, given non-dimensionally as ξG/λ: ξG/λ = 0 wave crest, 0 < ξG/λ < 0.5 wave front, ξG/λ = 0.5 wave trough, ξG/λ > 0.5 wave back.

Assuming linearity of the forces and moments as function of heel angles, the actual loads measured experimentally can be written in a non-dimensional form as in Eqs. 1 and 2. The inertia loads are negligible, since the encounter frequency is low:

$$Y^{\prime} = Y^{\prime}_{\varPhi } (\xi _{G} /\lambda ,\,\lambda /L,\,U)\varPhi$$
(1)
$$N^{\prime} \, = \, N^{\prime}_{\varPhi } (\xi_{\text{G}} /\lambda ,\lambda /L, \, U) \, \varPhi .$$
(2)

The forces and moments in sway and yaw are expressed by the heel angle Φ multiplied by the hydrodynamic coefficients \(Y^{\prime}_{\varPhi }\) and \(N^{\prime}_{\varPhi }\). These coefficients represent the effect of the ship’s static heel angle on the manoeuvring loads.

The experiments were performed in the Delft University of Technology towing tank. The vessel model was attached to the carriage using an oscillator capable of moving in six degrees of freedom. The forces and moments were measured on a frame installed between the model and the oscillator. The wave elevation was measured by a wave probe rigidly attached to the carriage at the same longitudinal location as the centre of gravity of the model, G.

During every run, the model was able to move vertically to maintain its vertical equilibrium attitude in the waves. The time traces of the motions and rotations in heave and pitch were calculated by a 3D time domain potential flow BEM which is described in Sect. 3. Each planned run for the captive model tests was reproduced numerically in advance, constraining the model in surge, yaw, sway, and heel, while being free to move in heave and pitch. These motions were used as input for the Hexapod which controls the model movements. To ensure the correct realization of the experiments, the full synchronization of carriage, wave-maker, and Hexapod was necessary. Figure 4 shows an example of the comparison between the computed prediction and the measured data resulting from the synchronization.

Fig. 4
figure 4

Comparison between the computed and measured time histories of the main outputs of the synchronization: wave elevation at model G (top), carriage speed (middle), and carriage position (bottom). The dotted line highlights the instant at which the measurement starts. In this figure, λ/L = 2 and Fr  = 0.48

Full size image

The synchronization phases can be described as it follows. At the run start, the wave-maker is activated: the model is out of the water until a stable wave train is generated. After this waiting time, the carriage starts automatically according to the speed time trace specified by the user input. At this point, the Hexapod is triggered and the model moves towards the desired wave position ξG/λ at its prescribed vertical position. Once the model reaches the desired position the measurement starts. After a complete or partial wave cycle, the carriage starts to decelerate, the model is lifted out of the water and the measurement ends. Figure 5 shows three photographs taken during a measurement run.

Fig. 5
figure 5

Examples of three different phases during a run. a The waves are generated, and the ship model is out of the water. The carriage is stationary. b The carriage has accelerated to its nominal speed and the model is in its initial position on the wave. The measurement starts. c Measurement interval: the ship model oscillates in heave and pitch according to the wave positions. The forces and moments, the wave elevation, and the vertical position of the model are being measured

Full size image

The synchronization process consists of two steps. First, it is necessary to know how the waves develop along the tank. There is a phase shift, φP, between the waves and the sinusoidal input signal from the wave-maker controller. The phase φP was obtained by means of a least-squares fitting of the signal of the wave probe positioned at the model’s starting location. The second step consists of the estimation of the longitudinal position in the tank corresponding to the first position of the model on the wave. For that, Eq. 3 is solved iteratively for time t as the independent variable, until the match between the carriage longitudinal position x*T and the desired wave elevation ς* is reached. The time t is summed to obtain the waiting time needed for the wave to be fully developed:

$$\varsigma ^{*} {\mkern 1mu} = {\mkern 1mu} \varsigma _{{\text{A}}} cos{\mkern 1mu} \left( {\omega {\mkern 1mu} t{\mkern 1mu} - {\mkern 1mu} k{\mkern 1mu} x^{*} _{{\text{T}}} \left( {t,{\mkern 1mu} U} \right){\mkern 1mu} + {\mkern 1mu} \varphi _{{\text{P}}} } \right).$$
(3)

To characterize the wave propagation details along the tank, an extensive series of wave measurements was carried out during the preparatory phase of the experiments. These measurements had two aims. The first aim is to set the correct amplitude for the input to the wave-maker, and to determine the time which is required to achieve a stable regular wave train. The second aim is to determine the celerity of the wave crests, making use of the definition of encounter frequency. The method consists of moving the carriage along with the wave at a high encounter frequency to be able to record several wave periods. The wave elevation was measured using the wave probe installed on the carriage. The model was not present at this stage. The wave encounter period was then measured, and the wave celerity was calculated according to Eq. 4. The wave amplitude and celerity are considered to be constant along the length of the tank:

$$\lambda /T \, = \, c \, = \, U/\left( {1 \, - \, T/T_{\text{E}} } \right).$$
(4)

2.3 Numerical correction of the model vertical equilibrium

The use of the calculated vertical position in the time domain (heave and pitch) as input to the model motions on the wave can have certain advantages; however, it introduced a potential error. The calculated vertical positions did not ensure vertical equilibrium in the model tests, resulting in a non-zero heave force and pitch moment measured during the runs. It meant that a new vertical position must be found such to satisfy the vertical equilibrium. The approach followed was the same as that presented in the work of [23]. As a first step, it is necessary to evaluate the sensitivity derivatives of the force and moments in heave σ and pitch θ. In this study, those derivatives were calculated numerically using the 3D time domain potential flow BEM described in Sect. 4, already introduced in this paper. The derivatives are evaluated by varying the model’s vertical attitude systematically at each longitudinal location in the wave. Figure 6 shows the outcome of this analysis on the heave force and pitch moments. Each point in the plot represents a different heave or pitch value at the location in the wave ξG/λ. The range of the values of heave σ and pitch θ is chosen accordingly to their maximum variation in the measurements.

Fig. 6
figure 6

Sensitivity coefficients of heave force Z′ (top row) and pitch moment M′ (bottom row) with respect to the variation of heave Δσ (left column) and pitch Δθ (right column) with respect to the equilibrium value. This figure refers to the condition 1 (λ/L = 1; Fr  = 0.38), at the location in the wave correspondent to ξG/λ = 0.5

Full size image

The new heave and pitch values can be calculated solving the system of equations:

$$\begin{aligned} Z^{\prime}\left( t \right) \, + \, Z^{\prime}_{\sigma } \Delta \sigma^{\prime}\left( t \right) \, + \, Z^{\prime}_{\theta } \Delta \theta \left( t \right) \, = \, 0 \hfill \\ M^{\prime}\left( t \right) \, + \, M^{\prime}_{\sigma } \Delta \sigma^{\prime}\left( t \right) \, + \, M^{\prime}_{\theta } \Delta \theta \left( t \right) \, = \, 0. \hfill \\ \end{aligned}$$
(5)

The terms Z′ and M′ are, respectively, the non-zero heave force and pitch moment measured in the tests. The variations in heave for the six conditions tested are, on average, about the 10% of the maximum heave excursion of the model on the wave. For pitch, the same averaged relative variation is around the 2.5%. Figure 7 shows the values of heave and pitch before and after the correction for a single condition.

Fig. 7
figure 7

Plots of the original measured vertical motions and the values after correction (top: heave; bottom: pitch). Condition 3 examined: λ/L = 1.5, Fr  = 0.48

Full size image

With the calculated variations in heave and pitch, it is possible to evaluate the new corrected sway force Y′ and yaw moment N′ using Eqs. 6 and 7. The sensitivity coefficients Y′σ, Y′θ, N′σ, N′θ are calculated similarly to the coefficients of heave force and pitch moment:

$$Y^{\prime} \, = \, Y^{\prime} \, + Y^{\prime}_{\sigma } \Delta \sigma + Y^{\prime}_{\theta } \Delta \theta$$
(6)
$$N^{\prime} \, = \, N^{\prime} \, + N^{\prime}_{\sigma } \Delta \sigma + N^{\prime}_{\theta } \Delta \theta .$$
(7)

2.4 Uncertainty analysis

The uncertainty of the measured experimental values was estimated following the ITTC Recommended Procedures and Guidelines no. 7.5-02 06-04 [32]. The sources of uncertainty considered in the experiments are: model length L, wave probe position xP, wave elevation ς, wave frequency ω, and measured loads f. The total uncertainty is constituted by the systematic errors connected to instrumentation and set-up biases, and by the 95% confidence limits evaluated by means of repeated runs. The main contributions to the total uncertainty are the wave amplitude and the repeatability of the measured loads. The contribution to the total uncertainty of the synchronization procedure is implicitly estimated by the confidence limits of the forces and wave elevation, calculated after ten measurement repetitions. This method was the only feasible one to assess the uncertainty of the wave–carriage–oscillator synchronization. The most accurate way would be the measure of the wave elevation at the instant at which the measurement starts, to assess the relative position wave model and, hence, the synchronization between them. However, this measurement is disturbed by the presence of the model and by the flow on the probe due to the forward motion. At this stage, it is considered that the repeatability of the runs is the most reasonable way to estimate the quality of the synchronization methods. The uncertainty of the manoeuvring coefficients obtained is evaluated according to Eq. 8. The uncertainty of the generic hydrodynamic coefficient URfΦ is made up of two terms: first, the sum of the ith load points uncertainty URfi squared; and second, the error of the linear fitting of the calculation of the coefficients, according to the Standard Error Estimate given in [33]. The parameter t is the coverage factor of the Student distribution for N data points. The results of the uncertainty analysis are shown in Fig. 8:

Fig. 8
figure 8

Percentage uncertainty of the measured manoeuvring coefficients for the six conditions considered. The values are averaged along the positions on the wave and relative to the coefficient maximum absolute value

Full size image
$$U_{{{\text{Rf}}\varPhi }} = \sum_{i} U_{\text{Rfi}}^{2} + \, t \, \Big(\sum_{i} \left( {f_{i} - \, f_{\varPhi } \varPhi } \right)^{2} /\left( {N - 2} \right) \,\Big )^{0.5} .$$
(8)

3 The numerical simulations

The numerical method utilized in this study was developed and validated for many seakeeping applications [34,35,36,37,38,39]. In more recent research, the mathematical tool was utilized in following sea problems [8, 10, 40]. The numerical model is a time domain-blended 3D BEM based on potential flow theory. The hull surface is discretized by planar quadrilateral panels, and is divided in below and above water geometry by a waterline defined by the running equilibrium position of the craft at speed in calm water, as shown in Fig. 9. This position represents the initial condition for the simulations. On the submerged geometry a transient Green function is specified, which expresses the influence of the ship hull on the free surface (memory effect), eliminating the need for an additional discretization of the free surface.

Fig. 9
figure 9

Hull discretization by quadrilateral panels at Fr  = 0.48

Full size image

The dynamic pressures due to the incoming flow are evaluated only on the fixed below water geometry. Hydrostatic loads (buoyancy), Froude–Krylov wave loads, cross-flow drag, and frictional resistance are specified on the actual submerged geometry, i.e., on the instantaneous wavy free surface. The linearization of the boundary conditions and the Green function around the flat waterline results in a less accurate prediction than their computation on the actual wavy free surface. However, the linearization drastically reduces the computational effort allowing this to be applied to a wide range of variables.

4 Results

In this section, the results of the experimental investigation are presented and discussed. The results are shown in terms of:

  • non-dimensional heel–sway hydrodynamic coupling coefficient, Y′Φ;

  • non-dimensional heel–yaw hydrodynamic coupling coefficient, N′Φ.

All the measured quantities refer to the reference frame in Fig. 3. The experiments were carried out for positive heel angles (model heeled to starboard). At each position on the wave, the hydrodynamic derivatives were calculated by linearly fitting the loads measured as a function of the heel angle. Figure 10 depicts the fitting of the heel-induced sway force and yaw moment on the front and on the back of the wave as function of the heel angle for one condition considered. The yaw moment is linear with the heel angle, whereas the sway force shows a slight non-linear behaviour over 10° when the vessel is on the front of the wave. For simplicity, a linear fitting of the loads was chosen in every position in the wave. An insight on the importance and the nature of this non-linear component must be addressed yet.

Fig. 10
figure 10

Non-dimensional sway force and yaw moment as function of the heel angle Φ for two positions in the wave. Left column: the vessel is in the front of the wave (ξG/λ = 0.3); right column: the vessel is in the back of the wave. Plots refer to Condition 4: Fr  = 0.47 and λ/L = 2

Full size image

The results are plotted in term of non-dimensional heel–sway and heel–yaw hydrodynamic coefficients as functions of the non-dimensional longitudinal position of the model centre of gravity in the wave, ξG/λ. The hull loads are measured according to the equilibrium vertical attitude of the model in the wave. The results are fitted along the wave locations with a sinusoidal signal of the same frequency as the excitation wave encounter frequency for the conditions considered. The hydrodynamic coefficients Y′Φ and N′Φ are compared with the calm water value at the respective ship speed; the calm water hydrodynamic coefficients were obtained in [19] and reported in Table 3.

Table 3 Values of the heel–sway and heel–yaw hydrodynamic coupling obtained in calm water
Full size table

The hydrodynamic coefficients are non-dimensional according to Eqs. 9 and 10. The heel angle Φ is expressed in radians:

$$Y^{\prime}_{\varPhi } = \, Y_{\varPhi } / \, \left( {0.5\rho \, U^{2} L^{2} } \right)$$
(9)
$$N^{\prime}_{\varPhi } = \, N_{\varPhi } / \, \left( {0.5\rho \, U^{2} L^{3} } \right).$$
(10)

The heel–sway coupling coefficients for the conditions tested are shown in Fig. 11.

Fig. 11
figure 11

Non-dimensional heel–sway coupling hydrodynamic coefficient Y′Φ as a function of the ship location on the wave. Left: Conditions 1 and 2, Fr = 0.38; centre: Conditions 3 and 4, Fr = 0.48; right: Conditions 5 and 6, Fr = 0.58. The dashed black line denotes the value of Y′Φ in calm water at the respective Froude number from [19]

Full size image

The amplitude and the mean value of the sinusoidal signals are greater for greater values of Froude number. Between the lowest speed Fr = 0.38 and the other two higher speed cases Fr = 0.48 and Fr = 0.58, a phase shift of about half wave length was observed. The variations with respect to the calm water values are quite significant. The value of Y′Φ is mostly negative at Fr = 0.38 for all the locations ξG/λ, meaning that, when heeled at starboard, the sway force is directed to port. For the higher speeds, the sign of Y′Φ changes from negative on the wave front to positive when the ship is located on the wave back.

The heel–yaw coupling coefficients N′Φ are shown in Fig. 12.

Fig. 12
figure 12

Non-dimensional heel–yaw coupling hydrodynamic coefficient N′Φ as a function of the ship location on the wave. Left: Conditions 1 and 2, Fr = 0.38; centre: Conditions 3 and 4, Fr = 0.48; right: Conditions 5 and 6, Fr = 0.58. The dashed black line denotes the value of N′Φ in calm water at the respective Froude number from [19]

Full size image

Unlike the values of N′Φ in calm water which are negative for the speed range investigated, in following waves, the heel–yaw coefficient changes sign. Whereas at Fr = 0.38 N′Φ is always positive for all the longitudinal locations in the wave, ξG/λ, for the other two cases, the coefficient is negative on the front of the wave, and positive on the back of the wave. Thus, on the front of the wave, a heel angle to starboard means that the coupling effect makes the vessel to turn to port. The opposite occurs on the back of the wave.

The heel-induced loads originate from the non-symmetrical hull submerged geometry and by the vertical position of the vessel in the wave. They are caused by the lift developed on the hull bottom, the Froude–Krylov, radiation and diffraction effects, and by more complex viscous phenomena such as the flow separation at the chine. Since only the total forces and moments are measured during a captive model experimental test, it is very hard to examine the characteristics of these loads in detail. Advanced numerical simulations (RANSE solvers) might provide a better insight in the study of these loads.

5 Utilization of the results

The main objective of this section is to present an empirical description of the manoeuvring loads induced by heel in following waves. Although these loads were measured for only a few cases, the results can be interpolated and extrapolated to other wavelengths and ship-speed conditions. The description considers the effect of the sway force and the yaw moment caused by a heel angle. It is useful to express these loads by means of the amplitude, mean value, and phase (see Eqs. 11 and 12). Those terms can be obtained by the least square fitting of their sinusoidal signal as functions of the location of the ship in the wave ξG/λ. This facilitates the expression of the loads in the wave due to the heel of the vessel, since they can be characterized by only three terms:

$$Y^{\prime}_{\varPhi } = \, A_{{Y^{\prime}\varPhi }} \cos (2\pi \, + \varphi_{{Y^{\prime}\varPhi }} ) \, + \, m_{{Y^{\prime}\varPhi }}$$
(11)
$$N^{\prime}_{\varPhi } = \, A_{{N^{\prime}\varPhi }} \cos (2\pi \, + \varphi_{{N^{\prime}\varPhi }} ) \, + \, m_{{N^{\prime}\varPhi }} .$$
(12)

Each of these terms can be plotted as a function of the Froude number and wave length; then, the values of the six experimental cases can be fitted using a plane, as shown in Fig. 13.

Fig. 13
figure 13

Mean values of the hydrodynamic coefficient N′Φ as a function of Fr and λ/L, and the correspondent fitting plane

Full size image

Equations similar to Eq. 13 can be written for the other terms related to the wave loads. Thanks to this fitting, the loads in the waves due to the heel angle can be expressed by several other combinations of wavelengths and Froude numbers. As a first approximation, a planar fit was chosen. The characteristic parameters of the heel-coupling coefficients depend with good approximation linearly to the Froude number and the wavelength:

$$A_{{N^{\prime}\varPhi }} = \, a_{1} Fr \, + \, a_{2} \lambda /L \, + \, a_{3} .$$
(13)

This empirical description of the heel-induced loads was used to correct the mathematical BEM described in Sect. 3. The manoeuvring loads computed by the BEMs are often not satisfactory; this correction allows a not perfect but reasonable agreement with the experimental results on a wide range of Fr and λ/L. In Fig. 14, the comparison between the measured values and the obtained ones by numerical simulations is depicted, for the mean value of the heel–yaw coupling coefficient. The coefficients are evaluated at several Froude numbers and wavelengths other than the six experimental cases, showing the same trend of the experimental outcomes.

Fig. 14
figure 14

Empirical description of the mean value of the heel–yaw coupling coefficient mN′Φ by means of the 3D BEM. Left: 3D view of the experimental and predicted values. Right: the same values are plotted but in two different planes, as a function of Fr (top-right) and of λ/L (bottom-right)

Full size image

Figure 15 shows a comparison of the sway force and the yaw moment at a heel angle between a measured experimental case and its numerical reproduction.

Fig. 15
figure 15

Comparison of measurement and the corrected prediction of sway force (top) and yaw moment (bottom) plotted against the vessel location in the wave. Condition examined: λ/L = 2.25, Fr = 0.58, and Φ = 12 deg

Full size image

6 The effect of the heel-induced loads in the following sea

In this section, the 3D BEM corrected with the heel-induced sway and yaw loads obtained in the experiments is used to simulate the behaviour of the high-speed craft in the following sea. The objective is to analyse the effect of the heel-induced loads on the inception of course dynamic instability such as broaching-to. The broaching is defined as specified in Eq. 13: both the yaw rate and the yaw rate acceleration being positive despite the maximum counter-action of the steering devices. The definition was taken from the following [11]:

$$r \, > \, 0, \, \dot{r} \, > \, 0, \, \delta \, = \, \delta_{\text{M}} .$$
(13)

The ship was free to move in six degrees of freedom in the seaway. The initial conditions of the simulations in terms of heave and pitch were set to ensure the vertical state of equilibrium in calm water for each of the speeds considered. Similarly, the thrust propulsion rate was set to match the calm water resistance and kept constant during the entire time loop of the simulation. The steering angle was set by an autopilot with a control algorithm given in Eq. 14. The autopilot is meant to simulate a response by the helmsman during a normal operation; it is aimed to counteract a certain change of heading and turning rate bringing the ship back again on a straight course. The steering parameters were: the proportional coefficient cδψ = 3 deg/deg; the damping coefficient bδr = 9.49 deg s/deg; the steering rate δ̇  = 10 deg/s; the maximum steering angle δM = 23 deg. The values were taken from the work of De Jong et al. [8]. The regular waves were ramped up with a sinusoidal function, within a time interval long enough to ensure a smooth start of the ship motions and stable outcomes:

$$\delta \, = \, b_{\delta r} \Delta r \, + \, c_{\delta \psi } \Delta \psi .$$
(14)

The investigation covers 7 vessel speeds equally spaced between Fr  = 0.3–0.6; for each speed 8 wavelengths are considered, between a minimum of λ/L =0.6 and a maximum of λ/L  = 3.0, resulting in 56 total conditions. The wave steepness coincides with the value used in the experiment, H/λ  = 0.06, and the initial wave heading angle μ is equal to − 20° in all the conditions simulated.

The effect of the heel-induced loads is analysed by comparing the broaching zones within the range of the conditions examined with and without the utilization of the heel-coupling terms. In the latter case, the coupling terms were set to zero by correcting the 3D BEM outcomes in a similar way to what done in Sect. 5. The results are presented in Fig. 15.

Figure 16 shows that the heel-induced sway force and yaw moment stabilize the high-speed craft, reducing the likelihood of dynamic course instability events occurrence. In the conditions considered, which are not extreme, broaching-to inception builds-up during the surf-riding phenomenon: in this situation, the vessel location is in the wave downslope near the through at ξG/λ  = 0.4–0.5. This is confirmed by the considerations in [9]. Although the coefficient N′Φ changes sign along the wave, at the surf-riding position, N′Φ is positive in all the conditions considered. According to the ship frame depicted in Fig. 3, when the waves act at quarter starboard the vessel starts yawing towards starboard beam-to-sea, while heeling towards port. Being the heel negative and the heel–yaw coupling coefficient positive, this results in a negative yaw moment caused by the vessel’s heel which counter-acts the positive destabilizing moment. This result extends the validity of the outcomes in [23] to a wider range of ship speeds and wave conditions. The dynamic behaviour of the high-speed craft is described by the plots of Fig. 17.

Fig. 16
figure 16

Broaching zone of the high-speed craft for μ = − 20 deg and H/λ = 0.06. Left: without heel-induced loads; right: with heel-induced loads. The red area identifies the broaching region

Full size image
Fig. 17
figure 17

Plots of the main time histories of one simulation in stern-quartering waves. The continuous line refers to the simulation without heel-induced loads where broaching-to occurs after 60 s; the dotted line refers to the simulation with heel-induced loads, where the ship experiences only a surf-riding

Full size image

7 Conclusions

This work investigated the hydrodynamic coupling between heel and the manoeuvring loads in sway and yaw in following waves for a high-speed craft. The heel-induced sway force and yaw moment were investigated experimentally by means of captive model tests in six conditions of model speeds and wave lengths. The measured data were utilized for an empirical formulation of these loads on a wider range of speeds and wavelengths. This formulation was implemented into a time domain 3D BEM, and the comparison between experimental and numerical results was presented.

The experimental tests carried out in this study and presented in Sect. 2.4 are based on a not common technique of synchronization of waves and model motions. This work proved that wave-maker, carriage, and model oscillator can be synchronized with a good level of accuracy at low–medium encounter frequency. Although the measured data showed a good reliability, a more rigorous procedure to estimate the uncertainty of the experimental technique is missing. This issue must be addressed in future studies.

The results of the experiments, presented in terms of non-dimensional hydrodynamic coefficients Y′Φ and N′Φ, showed that the coupling between heel and the manoeuvring loads in sway and yaw depends strongly on the location of the vessel in the wave. Furthermore, Y′Φ and N′Φ differ significantly from their respective values in calm water. The single contribution of the hydrodynamic lift, the wave-making effect, and incoming wave to the manoeuvring loads due to heel must be still clarified by deeper hydrodynamic insights. More accurate numerical methods can be used to investigate in detail this important phenomenon which affects significantly the dynamics of the ship in the seaway.

The experimental data were used to formulate an empirical description of the loads in sway and yaw due to heeling. This empirical description was used to correct a 3D BEM, with the aim of being able to characterize the heel-induced loads in several combinations of ship speeds and wavelengths. Commonly in manoeuvrability studies, the loads acting on the hull are expressed by polynomial empirical formulations, without solving any fluid equations. Such a characterization of the loads in following waves could allow also simple mathematical tools to qualitatively and quantitatively describe the behaviour of fast vessel in a seaway. Using the terms summarized in Table 4, it is possible to define these loads in simpler parametric mathematical models. The same approach can be pursued for any other parameters of the ship manoeuvrability. In other words, the experimental results can be used to implement the parametric mathematical models and to validate and improve practical 3D BEM, both widely used in the ship manoeuvrability discipline.

Table 4 Parameters of the planar fitting of the heel–sway and heel–yaw coupling coefficients, according to Eqs. 11, 12, and 13
Full size table

The corrected 3D BEM was used to assess the effect of the heel–yaw and heel–sway hydrodynamic coupling into the inception of broaching-to in the following sea. The heel-induced loads cause the ship to be more stable and then reducing the likelihood of broaching inception. The results agree with the investigation of Hashimoto et al. [23], confirming the validity of these considerations to several wave and ship-speed conditions. The study of Renilson and Manwarring [18] shows instead an opposite result of the effect of the heel-induced loads into the inception of broaching-to. It must be said that this work was based on a containership, which is naturally very different from a semi-displacement vessel or a high-speed craft. However, most importantly, it considered only the heel-induced loads measured in calm water as first approximation for the more complex dynamics in a seaway. This confirms another fact shown by this work: the nature of heel–sway and heel–yaw coupling in the following sea is very different, even opposite, from the case in calm water. The effects originating from the incoming waves are more significant that the dynamics of the lift and wave-making in calm water, especially for the heel–yaw hydrodynamic coupling N′Φ.