Abstract
In this study, a practical maneuvering simulation method is presented considering the roll-coupling effect by extending an ordinal simulation model (3D-MMG model) proposed by Yasukawa and Yoshimura (J Mar Sci Technol 20:37–52, 2015), and adding the motion equation of roll. The roll moment acting on the hull is estimated by multiplying the hull lateral force with the vertical acting point. With respect to the surge force, lateral force, and yaw moment, the derivative expression model is employed. Subsequently, hydrodynamic derivatives with the exception of the roll-related terms are obtained by a captive model test based on the 3D-MMG model. The roll-related derivatives and the vertical acting point of the hull lateral force are estimated by simple formulae constructed based on the experimental data of four ship models. To validate the proposed simulation method, turning simulations are conducted for a pure car carrier model with variations in the metacentric height \({\overline{\mathrm{GM}}}\) and are compared with free-running model test results. The simulation method exhibits sufficient accuracy with respect to its practical use and is useful to conventionally predict turning motions by considering the roll-coupling effect.











Similar content being viewed by others
Abbreviations
- \(A_\mathrm{D}\) :
-
Advance
- \(A_\mathrm{R}\) :
-
Rudder profile area
- a, b :
-
Coefficients of the roll-extinction curve
- \(a_\mathrm{H}\) :
-
Rudder force increase factor
- \(a_{24}, a_{26}, a_{46}\) :
-
Added masses coupled among sway, roll, and yaw
- B :
-
Ship breadth
- \(C_\mathrm{b}\) :
-
Block coefficient
- \(c_0, c_1\) :
-
Constants in the proposed formulae
- \(D_\mathrm{P}\) :
-
Propeller diameter
- \(D_\mathrm{T}\) :
-
Tactical diameter
- d :
-
Ship draft
- \(F_\mathrm{N}\) :
-
Rudder normal force
- \(Fn\) :
-
Froude number based on ship length
- \(F_x, F_y\) :
-
Surge force and lateral force acting on the ship, respectively
- \(f_{\alpha }\) :
-
Rudder normal force gradient coefficient
- \({\overline{\mathrm{GM}}}\) :
-
Metacentric height
- g :
-
Gravity acceleration
- \(H_\mathrm{R}\) :
-
Rudder span length
- \(I_{xx}, I_{zz}\) :
-
Moment of inertia of the ship around x- and z-axes, respectively
- \(J_\mathrm{P}\) :
-
Propeller advance ratio
- \(J_{xx}, J_{zz}\) :
-
Added moment of inertia around x- and z-axes, respectively
- \({\overline{\mathrm{KM}}}\) :
-
Metacenter height above baseline
- \(K_\mathrm{T}\) :
-
Propeller thrust open water characteristic
- \(K_{{{\dot{\phi }}}}\), \(K_{{{\dot{\phi }}}{{\dot{\phi }}}}\) :
-
Roll-damping coefficients
- \(k_{xx}\) :
-
Radius of roll gyration including added moment of inertia with respect to the roll
- \(k_2, k_1, k_0\) :
-
Coefficients that represent \(K_\mathrm{T}\)
- L :
-
Ship length between perpendiculars
- \(l_\mathrm{P}\) :
-
Longitudinal coordinate of the propeller position in the formula for \(\beta _\mathrm{P}\)
- \(l_\mathrm{R}\) :
-
Effective longitudinal coordinate of the rudder position in the formula for \(\beta _\mathrm{R}\)
- \(M_x, M_z\) :
-
Roll moment and yaw moment acting on ship around the center of gravity, respectively
- m :
-
Ship’s mass
- \(m_x\), \(m_y\) :
-
Added masses of the x-axis direction and y-axis direction, respectively
- \(n_\mathrm{P}\) :
-
Propeller revolution
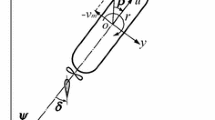
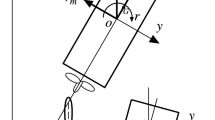
- \(o-xyz\) :
-
Horizontal body-fixed coordinate system considering the origin at midship
- \(o_0-x_0y_0z_0\) :
-
Space-fixed coordinate system
- \(R_0'\) :
-
Ship resistance coefficient in straight movement
- \(R^2\) :
-
Coefficient of determination
- r :
-
Yaw rate
- T :
-
Propeller thrust
- t :
-
Time
- \(t_\mathrm{P}\) :
-
Thrust deduction factor
- \(t_\mathrm{R}\) :
-
Steering resistance deduction factor
- U :
-
Resultant speed (\(=\sqrt{u^2+v_\mathrm{m}^2}\))
- \(U_0\) :
-
Approach ship speed
- \(U_\mathrm{R}\) :
-
Resultant inflow velocity to the rudder
- u, v :
-
Surge velocity and lateral velocity at the center of gravity, respectively
- \(u_\mathrm{R}\), \(v_{\rm{R}}\) :
-
Longitudinal and lateral inflow velocity components of the rudder, respectively
- \(v_\mathrm{m}\) :
-
Lateral velocity at midship
- \(w_\mathrm{P}\) :
-
Effective wake fraction at the propeller position in maneuvering motions
- \(w_{\mathrm{P}0}\) :
-
Effective wake fraction at the propeller position in straight movement
- X, Y, N, K :
-
Surge force, lateral force, yaw moment, and roll moment with the exception of added mass components, respectively
- \(X_\mathrm{H}\), \(Y_\mathrm{H}\), \(N_\mathrm{H}\), \(K_\mathrm{H}\) :
-
Surge force, lateral force, yaw moment, and roll moment acting on the ship hull with the exception of added mass components, respectively
- \(X_\mathrm{P}\) :
-
Surge force due to the propeller
- \(X_\mathrm{R}\), \(Y_\mathrm{R}\), \(N_\mathrm{R}\), \(K_\mathrm{R}\) :
-
Surge force, lateral force, yaw moment, and roll moment by steering, respectively
- \(x_{G}\) :
-
Longitudinal coordinate of the center of gravity of the ship
- \(x_\mathrm{H}\) :
-
Longitudinal coordinate of the acting point of the additional lateral force component induced by steering
- \(x_\mathrm{P}\) :
-
Longitudinal coordinate of the propeller position
- \(x_\mathrm{R}\) :
-
Longitudinal coordinate of the rudder position (= \(-\,0.5\) L)
- \(Y_{v}', N_{v}'\) :
-
Linear hydrodynamic derivatives with respect to the lateral velocity
- \(Y_{r}', N_{r}'\) :
-
Linear hydrodynamic derivatives with respect to the yaw rate
- \(Y_{\phi }', N_{\phi }'\) :
-
Linear hydrodynamic derivatives with respect to the roll
- \(z_{G}\) :
-
Vertical coordinate of the center of gravity of the ship
- \(z_\mathrm{H}\) :
-
Vertical coordinate of the acting point of the hull lateral force
- \(z_\mathrm{P}\) :
-
Vertical coordinate of the propeller position
- \(z_\mathrm{R}\) :
-
Vertical coordinate of the acting point of the rudder force
- \(z_\mathrm{v}\) :
-
Vertical coordinate of the acting point of the hull lateral force in the oblique towing condition
- \(\alpha _\mathrm{R}\) :
-
Effective inflow angle to the rudder
- \(\alpha _\mathrm{z}\) :
-
Vertical acting point of the lateral added mass component \(m_y\)
- \(\beta \) :
-
Hull drift angle at midship
- \(\beta _\mathrm{P}\) :
-
Geometrical inflow angle to the propeller in maneuvering motions
- \(\beta _\mathrm{R}\) :
-
Effective inflow angle to the rudder in maneuvering motions
- \(\gamma _\mathrm{R}\) :
-
Flow-straightening coefficient
- \(\delta \) :
-
Rudder angle
- \(\eta \) :
-
Ratio of the propeller diameter to the rudder span (\(=D_\mathrm{P}/H_\mathrm{R}\))
- \(\phi \) :
-
Roll angle
- \(\phi _\mathrm{S}\) :
-
Steady heel in turning
- \(\kappa \) :
-
Experimental constant for expressing \(u_\mathrm{R}\)
- \(\nabla \) :
-
Displacement volume of the ship
- \(\psi \) :
-
Ship heading
- \(\rho \) :
-
Water density
- \(\varepsilon \) :
-
Ratio of the wake fraction at the propeller and rudder positions
References
Eda H (1980) Rolling and steering performance of high speed ships. In: Proceedings of the 13th symposium on naval hydrodynamics, Tokyo, pp 427–439
Hirano M, Takashina J (1980) A calculation of ship turning motion taking coupling effect due to heel into consideration. Trans West Jpn Soc Nav Architects 59:71–81
Son K, Nomoto K (1982) On the coupled motion of steering and rolling of a high speed container ship. Nav Archit Ocean Eng Soc Nav Architects Jpn 20:73–83
Fossen TI (1994) Guidance and control of ocean vehicles. Wiley, New York
Yasukawa H, Yoshimura Y (2014) Roll-coupling effect on ship maneuverability. Ship Technol Res 61:16–32
Kim YG, Kim SY, Kim HT, Lee SW, Yu BS (2007) Prediction of the maneuverability of a large container ship with twin propellers and twin rudders. J Mar Sci Technol 12:130–138
Yasukawa H, Yoshimura Y (2015) Introduction of MMG standard method for ship maneuvering prediction. J Mar Sci Technol 20:37–52
Wang XG, Zou ZJ, Xu F, Ren RY (2014) Sensitivity analysis and parametric identification for ship manoeuvring in 4 degrees of freedom. J Mar Sci Technol 19:394–405
Blanke M, Jensen AG (1997) Dynamic properties of a container vessel with low metacentric height. Trans Inst Meas Control 19(2):78–93
Dash AK, Chandran PP, Khan MK, Nagarajan V, Sha OP (2016) Roll-induced bifurcation in ship maneuvering under model uncertainty. J Mar Sci Technol 21:689–708
Fukui Y, Yokota H, Yano H, Kondo M, Nakano T, Yoshimura Y (2016) 4-DOF mathematical model for manoeuvring simulation including roll motion. J Jpn Soc Nav Architects Ocean Eng 24:167–179 (in Japanese)
Hamamoto M, Kim Y (1993) A new coordinate system and the equations describing manoeuvring motion of a ship in waves. J Soc Nav Architects Jpn 173:209–220 (in Japanese)
Masuyama Y, Nakamura I, Tatano H, Takagi K, Miyakawa T (1992) Sailing performance of ocean cruising yacht by full-scale sea test (part 1: steady sailing performance and dynamic performance in waves). J Soc Nav Architects Jpn 172:349–364 (in Japanese)
Masuyama Y, Nakamura I, Tatano H, Sakaguchi K, Kanekiyo T (1993) Sailing performance of ocean cruising yacht by full-scale sea test (part 2: maneuverability and tacking performance). J Soc Nav Architects Jpn 174:377–388 (in Japanese)
Yoshimura Y (1984) Mathematical model for the manoeuvring ship motion in shallow water. J Kansai Soc Nav Architects Jpn 200:41–51 (in Japanese)
Yasukawa H, Hirata N, Yamazaki Y (2018) Effect of bilge keels on maneuverability of a fine ship. J Mar Sci Technol 23:302–318
Acknowledgements
This study was supported by JSPS KAKENHI Grant number JP26249135.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Captive model test with variations in the heel
Appendix: Captive model test with variations in the heel
To capture the heel effect on the hydrodynamic force characteristic, oblique towing test (OTT) and circular motion test (CMT) with variations in the heel angle were performed in the Hiroshima University Towing Tank (length: 100 m, width: 8 m, water depth: 3.5 m). The OTT and CMT are tests to measure the hydrodynamic forces acting on the ship model in oblique moving and/or steady turning.
1.1 Outline
The captive model tests were performed using a PCC model with a ship length of 2 m as mentioned in Sect. 4.1 under a condition with a rudder and without a propeller. In the tests, surge force, lateral force, and yaw moment around midship and roll moment were measured for the fixed model using a four-component dynamometer. However, the roll moment was measured only in \(\phi =0^\circ \). Ship speed U in the tests was 0.651 m/s (and this is equivalent to 12.0 kn for a full-scale ship, \(Fn=0.147\)). The measurements were constructed for the hull drift angle \(\beta \) from \(-\,20^\circ \) to \(20^\circ \) every \(5^\circ \), non-dimensional yaw rate \(r'\) from \(-\,0.3\) to 0.3 with the step 0.1, and heel angle \(\phi \) of \(0^\circ \), \(5^\circ \), \(10^\circ \), and \(15^\circ \).
The four-component dynamometer was arranged above the still-water surface because the internal space of the ship model was limited. Subsequently, the moment component due to the centrifugal force (inertia force component) is induced in the measured roll moment, which was deduced from the measured roll moment using other measured force components. The roll moment around the x-axis located on the still-water surface was obtained by converting the resulting roll moment. The static restoring roll moment was deduced from the results. The converted roll-moment coefficient is denoted by \(K_\mathrm{H}'\). Also, the test results for the surge force, lateral force, and yaw-moment coefficients are denoted by \(X_\mathrm{H}'\), \(Y_\mathrm{H}'\), and \(N_\mathrm{H}'\), respectively.
1.2 Test results
Figure 12 shows test results of \(X_\mathrm{H}'\), \(Y_\mathrm{H}'\), \(N_\mathrm{H}'\), and \(K_\mathrm{H}'\) in \(\phi =0\) that were obtained by OTT. In the figure, black circle means the averaged value of the measured time history data as the non-dimensional form. Error bars of the standard deviation are also plotted. The standard deviation is almost the same at the different hull drift angle \(\beta \) for each \(X_\mathrm{H}'\), \(Y_\mathrm{H}'\), \(N_\mathrm{H}'\) and \(K_\mathrm{H}'\). The averaged standard deviation (Ave. SD) in the different \(\beta \) is also indicated in the figure. Ave. SDs of \(N_\mathrm{H}'\) and \(K_\mathrm{H}'\) are almost the same, and ave. SD of \(X_\mathrm{H}'\) is about 40% smaller than that of \(Y_\mathrm{H}'\). Further, we found that the ave. SD is almost the same with variations in the heel angle for each \(X_\mathrm{H}'\), \(Y_\mathrm{H}'\), \(N_\mathrm{H}'\) and \(K_\mathrm{H}'\), and increases about two times for the measured data in CMT (with yaw motion) when compared with that in OTT (without yaw motion). It was confirmed that there is no big problem in the measurements.
Figure 13 shows test results of \(X_\mathrm{H}'\), \(Y_\mathrm{H}'\), and \(N_\mathrm{H}'\) in different heel angles \(\phi \). In the figure, dotted lines represent the fitting results using Eqs. (25) to (27). The roll-related hydrodynamic derivatives are listed in Table 6. Figure 14 shows test results of \(X_\mathrm{H}'\), \(Y_\mathrm{H}'\), and \(N_\mathrm{H}'\) for \(r'=0\). The roll effect significantly appears in the yaw moment.
Subsequently, the vertical acting point of hull lateral force is considered to discuss the roll moment on the hull. Figure 15 shows the roll-moment coefficient \(K_\mathrm{H}'\) relative to the lateral-force coefficient \(Y_\mathrm{H}'\) in \(\phi =0^\circ \). The inclination of \(K_\mathrm{H}'\) to \(Y_\mathrm{H}'\) denotes the vertical acting point of the lateral force \(z_\mathrm{H}\). In the figure, the results are classified into three categories, namely OTT results (“Pure Sway” in the graph), CMT results without \(\beta \) (“Pure Yaw”), and CMT results with \(\beta \) (“Sway + Yaw”). Mean lines of \(K_\mathrm{H}'\) relative to \(Y_\mathrm{H}'\) are drawn for each result in the figure. Table 8 shows the non-dimensional vertical acting point \(z_\mathrm{H}'(\equiv z_\mathrm{H}/L)\) for each result. In “Pure Sway,” \(z_\mathrm{H}'\) is positive. Conversely, in “Pure Yaw,” \(z_\mathrm{H}'\) is negative, and this indicates that the vertical acting point is located above the free surface. In “Sway+Yaw,” \(z_\mathrm{H}'\) is positive although the absolute value is approximately \(60\%\) of the value in “Pure Sway.” Thus, the vertical acting point of hull lateral force corresponds to different values based on the maneuvering mode such as oblique moving and turning. The reason is not clear in the present study. A similar result was obtained by Fukui et al. [11].
About this article
Cite this article
Yasukawa, H., Sakuno, R. & Yoshimura, Y. Practical maneuvering simulation method of ships considering the roll-coupling effect. J Mar Sci Technol 24, 1280–1296 (2019). https://doi.org/10.1007/s00773-019-00625-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00773-019-00625-4