1 Introduction

Ocean current energy is a promising power resource for Japan since the Kuroshio Current, which passes near the Japanese coast, is one of the strongest ocean currents in the world. A floating type ocean current turbine system has been developed as a future commercial system [1, 2]. The full-scale system is planned to have two horizontal turbines of 40 m diameter and to float 50 m below the sea surface tethered to a single mooring line.

Since the system has a weather vane function, the system can change its direction according to the current direction. Although the submergence depth is varied due to the variation of current speed, the depth can be adjusted by a buoyancy control system when the change of current speed is slow. However, if the variation is rapid, the blade pitch control system should be used to respond to the corresponding rapid change of the thrust force to maintain the submergence depth [3]. If the current speed is varied in space, horizontal motions are induced mainly due to the difference of thrust force between the two turbines. From the view point of structural design, the variation of current speed induces a fluctuating blade load, which affects the fatigue life of the blade and the drive train. The variation of current speed also induces undesirable fluctuations in the output power.

The variation of ocean current speed has been studied by oceanographers so far. They mainly focused on the slow variation (\(<10^{-3}\) Hz) to understand the meso-scale characteristics of the flow or the high-frequency turbulence (\(>1\) Hz) to know the dissipation rate [4]. From the engineering point of view, it is crucial to know the unsteady characteristics of the flow because it leads to the above-mentioned phenomena, which are mainly induced by the intermediate-frequency turbulence. Thus, it is important to conduct an engineering analysis of the intermediate-frequency range.

The quantification of turbulence in the ocean is not trivial. Many works within the ocean engineering and oceanography literature describe the design, setup, deployment, and analysis necessary to observe and process raw measurement data (for example, [5,6,7]). Recently, several projects have been conducted to form a set of guidelines for a tidal turbine design with a specific focus on the turbulence in the intermediate-frequency range (for example, [8,9,10]). However, the ocean current data in this frequency range are limited because the flow axis of ocean currents are far from the shoreline and the water depth is usually deep. Thus, we conducted ocean current measurements near Kuchinoshima Island specific to the above-mentioned ocean current turbine project. In this paper, we mainly focus on the data processing and characterization of turbulence as the first step to establish environmental input data for the simulation-based design of ocean current turbines.

2 Observations

2.1 Location of measurements

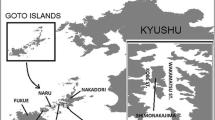
The measurements were taken within the Tokara Strait offshore of Kuchinoshima Island. The coordinates for the observed data are (129\(^\circ\)51′48″E, 30\(^\circ\)03′16″N). The well-known Kuroshio Current, which is known to undergo decadal meandering [11], consistently flows through this strait. The Signature 500 ADCP and Vector ADV were mounted on the seabed facing upward. The deployment location was on a ridge in the seabed northwest of Kuchinoshima in water depth of approximately 32 m as shown in Fig. 1. The ridge was quite convenient to setup the measurement, since the water depth was shallow while the flow axis of the Kuroshio Current passes through the area, although considerable influence on the current from the bathymetry was expected.

Fig. 1
figure 1

Bathymetry at the observation site near Kuchinoshima Island

Full size image

2.2 Instrument settings

Approximately, 24-h usable data were obtained from the measurement campaign. The limited time duration was a consequence of weather condition constraints on the deployment operations. Although the duration is short the data are sufficient to characterize the turbulence. While the full water column of 32 m was measured, due to data quality issues the analysis is limited up to 23 m from the seabed in some instances.

The Nortek Signature 500 Acoustic Doppler Current Profiler (ADCP) and Nortek Vector Acoustic Doppler Velocimeter (ADV) are both tools for measuring velocities in ocean environments. The Signature 500 offers the capability to measure velocities at multiple points within the water column. It uses four beams slanted at 25\(^\circ\) and a fifth vertical beam which allows for a true measurement of vertical velocities. The Vector uses three beams to measure velocities at a single point only; however, it can sample at very high frequencies. We took continuous measurements at 4 and 16 Hz for the Signature 500 and Vector, respectively. Table 1 shows the parameter settings used for the observations. The data used in the analysis for this work are from the Signature 500 because we are interested in turbulence characteristics throughout the water column. We measured at 1 m increments from the seafloor to the seabed using the Signature 500. The high-frequency Vector data served as a check to the Signature 500 data but it is limited to a single point in the water column 1 m from the seabed.

Table 1 Observation parameters
Full size table

2.3 Raw data

The current flow has a shear profile and varies widely in direction. Figures 2 and 3 show the raw data of speed and direction, respectively, from the Signature 500. The deployment begins approximately at 10:30 on Jan. 15, 2016 and ends shortly before 12:00 on Jan. 16, 2016.

Fig. 2
figure 2

Raw signature 500 ADCP speed data

Full size image
Fig. 3
figure 3

Raw signature 500 ADCP directional data

Full size image

During the deployment duration on average a near linear speed profile exists. The maximum speed profile similarly shows a generally linear profile. Figures 4 and 5 show the average and maximum speed profiles from the seabed up to 23 m.

Fig. 4
figure 4

Average speed profile for 23 bins above the seabed

Full size image
Fig. 5
figure 5

Maximum speed profile for 23 bins above the seabed

Full size image

2.4 Data quality

It is well known that the data quality near the sea surface is poor because of side lobe contamination. In addition, the very high water clarity at Kuchinoshima led to issues regarding data quality. High water clarity can lead to corresponding low signal strength and correlation and, therefore, possibly to low data quality. The time domain is divided into 30-min ensembles and the water column is divided into 1 m bins. Figure 6 shows the quality of the ADCP data on a bin/ensemble basis. The figures display in black, data blocks with a minimum correlation value of 50% and a minimum signal amplitude of 30%. Data that do not meet these criteria are displayed in white. We apply this definition of data quality based on the work of Guerra Paris [23] and an analysis of our raw data amplitude and correlation signals. The first few ensembles and last several ensembles in the figure were when the ADCP was being deployed and retrieved, respectively. Throughout the deployment duration the bins above 23 m returned low-quality data. As such the analysis in this work largely focuses on bins 1–23.

Fig. 6
figure 6

Analysis of data quality per bin/ensemble

Full size image

3 Data analysis and engineering aspects

In this section, we consider aspects of the current flow of interest to the engineering design of ocean current turbines. Often numerical simulations are employed during the design stage. Site-specific current flow characteristics can, therefore, serve as useful input to these simulations to produce realistic performance and loading predictions.

3.1 Spectral analysis

Publicly available MATLAB scripts [23] for 5 beam ADCP data analysis were adapted to analyze our Signature 500 observational data. The time domain is divided into 30-min ensembles. On a per bin basis, each ensemble is spectrally analyzed using a Welch’s overlapped segment averaging method to compute the turbulent kinetic energy spectrum. A representative spectrum is shown in Fig. 7 which is the spectrum for Ensemble 30, Bin 15 (in the middle of the water column). A peak occurs at slightly above \(10^{-1}\) Hz that is attributed to ocean waves. The spectrum shows a noise floor beginning at around 0.5 Hz. Figure 8 shows the spectrum from the ADV data. The higher sampling frequency allows for a larger frequency domain. The ADV spectrum shows no peak because the measurement position at 1m from the seabed is far removed from wave effects. The two figures show an exponential decay in the inertial range that approaches the theoretical \(f^{-5/3}\) value. While a large range exists over the total number of ensembles, on average the decay rate was \(f^{-1.35}\) for the ADCP Bin 15 data and \(f^{-1.53}\) for the ADV data.

Fig. 7
figure 7

(Top) Bin 15 speed–time history. (Bottom) ADCP spectral analysis for Ensemble 30 of Bin 15

Full size image
Fig. 8
figure 8

(Top) ADV speed–time history. (Bottom) ADV spectral analysis for Ensemble 18

Full size image

3.1.1 Noise floor

ADCP instruments use the Doppler shift of acoustic signals reflected from particles in the current flow to estimate the water velocity. Inherent to ADCP measurements are discrepancies which result from errors in the frequency change or phase shift of the reflected pulse. Many factors including the flow conditions, the processing scheme within the ADCP equipment, operational mode, and bin size contribute to Doppler noise [18].

Following the work of Richard [19], we know that Kolmogorov’s theory tells us in the inertial range the turbulent kinetic energy density (TKED) varies with wave number as

$$\begin{aligned} \mathrm{TKED}(k)=C\epsilon ^{2/3}k^{-5/3}, \end{aligned}$$
(1)

where C is the Kolmogorov constant and \(\epsilon\) is the turbulent kinetic energy dissipation rate. Employing the frozen turbulence hypothesis we relate frequency f of turbulent phenomena to wave number by \(f=k/U\). Here we assume velocity fluctuations are small compared to the mean flow speed U which advects the turbulent eddies. Given that the TKED is equal to the power spectral density (PSD), we know in the inertial range

$$\begin{aligned} S(f)=Kf^{-5/3}, \end{aligned}$$
(2)

with K being a constant. We expect the spectra of our data to exhibit a similar decay to this \(f^{-5/3}\) shape in the inertial range and tend to 0 at high frequency. However, at high frequencies, the measured spectrum is saturated by noise and converges to a noise PSD value. In terms of a spectral analysis, Doppler noise can be considered similar to white noise adding variance to the signal.

$$\begin{aligned} \sigma _\mathrm{measured}^2=\sigma _\mathrm{physical}^2+\sigma _\mathrm{noise}^2. \end{aligned}$$
(3)

Taking all this into consideration, we estimate Doppler noise by averaging the high-frequency end of the horizontal speed spectra, where the spectrum becomes flat due to noise saturation. This is illustrated in the bottom plot of Fig. 7. Denoting this value N, the noise-induced variance \(\sigma _\mathrm{noise}^2\) is equal to the integral of N over the bandwidth of the spectra. It is noted that the frequency at which the onset of noise saturation occurs is smaller than the sampling frequency. This is at a bit higher frequency than the wave frequency, and 0.5 Hz is supposed to be enough to estimate the motion of the current turbine. However, if a higher frequency range, say \(1-10\) Hz, is required to investigate the vibration of blade and drive train, using ADV is recommended since the noise floor starts at a much higher frequency as shown in Fig. 8 even though ADVs can only measure at a single point.

3.2 Turbulence characteristics

The current velocity can be decomposed into a mean (\(\bar{{{u}}}\)) and perturbation (\({{u}}'\)):

$$\begin{aligned} {{u}}=\bar{{{u}}}+{{{u}}'}, \end{aligned}$$
(4)

where \({{u}}=u{{i}}+v{{j}}+w{{k}}\).

3.2.1 Turbulence intensity metric

Turbulence intensity is a standard metric used in the wind turbine industry [13, 14] and is commonly used in the tidal power research field [15]. It is given by

$$\begin{aligned} I=\frac{\sqrt{\,\overline{u'^{2}}-n^{2}}}{\bar{u}}. \end{aligned}$$
(5)

Here \(n^2\) is the noise-induced variance \(\sigma _\mathrm{noise}^2\) associated with ADCP instruments as described above. In general, the horizontal current velocity drives the current turbines and thus is the focus of our interest. The vertical component of velocity is minimal in our data so we only consider the horizontal turbulence intensity in this work.

The turbulence intensity can be calculated as a function of time; however, attention must be paid to time durations of slack current, in which the mean speed approaches zero [20]. Under this circumstance, the denominator goes to zero causing the turbulence intensity value to blow up. These slack flow periods may occur due to the tidal patterns or fluctuations in the Kuroshio Current. Such very low speed conditions result in near-zero energy extraction since there is nearly no forcing on the turbine blades but lead to misleadingly high-turbulence-intensity values. To address this, a filter is applied based on the mean speed. A speed filter value of 0.35 m/s was selected through an iterative process to remove instances of turbulence intensity spikes yet maintain sufficient data time history. Only time durations for which the mean speed was larger than 0.35 m/s was used in the computation for average turbulence intensity. Figure 9 shows the results for the profile of average turbulence intensity.

The profile shows a consistent region from 1 to 15 m above the seabed of approximately 10% turbulence intensity. Above approximately 18 m above seabed the average turbulence intensity increases dramatically. This is assumed to be a consequence of the transition to the upper water column that is identified as a region of poor-quality data. This 10% turbulence intensity value is consistent with many sites studied in the literature concerning quantification of turbulence for ocean current and tidal power [21, 22].

Fig. 9
figure 9

Turbulence intensity variation throughout the water column

Full size image

3.2.2 Integral scales

Although turbulence intensity is a helpful metric for determining loads and expected energy production from a turbine, it does not address spatial and temporal structures of turbulence. Integral timescales and length scales determined from velocity autocorrelation functions offer a better physical description of turbulence. These scales are a measure how long the turbulent eddies remain correlated and their size, respectively [16]. These eddies represent typical flow structures current turbines would interact with.

The autocorrelation functions of the fluctuating terms of velocity components are used to determine the integral timescales. The streamwise autocorrelation function is given as

$$\begin{aligned} R_{uu}(\tau )=\frac{R(u'(t),u'(t+\tau ))}{\sigma _u^2}, \end{aligned}$$
(6)

where \(\sigma _u\) is the standard deviation.

We focused on the time index range of 216,000–218,400 of Ensemble 30 as this is a high flow speed–time duration. As can be seen in Fig. 10 there is a great variability in the autocorrelation within this time duration. We used an averaged autocorrelation function over 10-min to get a representative autocorrelation function. The autocorrelation function decays as the time lag increases and shows a degree of periodicity attributable to low-frequency oscillations in the flow. This behavior has similarly been reported by Garcia Novo [17]. The average autocorrelation function is integrated up to the first zero crossing to determine the integral timescale as in Eq. 7 and as shown in Fig. 10 for the case of streamwise autocorrelation function for Bin 15.

$$\begin{aligned} T_i=\int _{\tau =0}^{\tau (R_{ii}(\tau )=0)}\! R_{ii}(\tau )\mathrm{d}\tau . \end{aligned}$$
(7)
Fig. 10
figure 10

Streamwise autocorrelation for Ensemble 15 of Bin 15

Full size image

Starting at around 18 m from the seabed and above the integral timescales becomes very small. Figure 11 shows the autocorrelation function for Bin 20 which is representative of the other bins in this vertical range. The oscillatory behavior increases and the first oscillation briefly dips below the zero crossing. This results in very small integral timescales. If we disregard this brief initial dip, the integral timescales remain similar to those lower in the water column.

Fig. 11
figure 11

Streamwise autocorrelation for Ensemble 15 of Bin 20

Full size image

To calculate the integral length scale, Taylor’s frozen turbulence hypothesis is used as in the following equation, where U is the mean flow speed:

$$\begin{aligned} L_i=U T_i. \end{aligned}$$
(8)

The profiles of streamwise, transverse, and vertical integral timescales for the high speed flow time duration is shown in Fig. 12. The profile for mean speed is also overlaid on the same figure. The integral length scale is computed based on these profiles and the max time and length scales are shown in Table 2.

Fig. 12
figure 12

Profiles of integral timescales and mean speed for a high speed flow duration

Full size image
Table 2 Integral timescales and integral length scales during high flow speed
Full size table

3.3 Influence of bathymetry and directional dependence

As we saw in Fig. 3 the flow direction varies with time and is not consistent throughout the water column. The range of flow directions is shown in Fig. 13 which plots the time history of flow direction at Bin 15. The flow direction ranges from 100\(^\circ\) to \(-100^\circ\). For high speed flows there is little change in flow direction throughout the water column as seen in Fig. 14. However, for low speed flows there is considerable change in the flow direction. Figure 14 shows a variation of over 90\(^\circ\) throughout the water column for this case. This directional and fluctuation information is useful to the turbine designer to understand and account for in the turbine design and for performance models.

It was expected that the ridge bathymetry would influence the turbulence characterization as the flow direction changes. The 24-h measurement duration precludes observing several tidal and current flow cycles from which bathymetry effects may become evident. It is presumed that the increase in time averaged turbulence intensity standard deviation (see Fig. 9) in the lower portion of the water column is related to the ridge bathymetry. More data are necessary to consider the influence of bathymetry on these effects.

Fig. 13
figure 13

Direction and speed history for Bin 15

Full size image
Fig. 14
figure 14

Direction and speed profiles plots of increasing bin number for increasing speed for a high-speed flow case (in circles) and for a low-speed case (in x’s)

Full size image

3.3.1 Wave effects

Next we consider the potential effect of waves on the current measurements. An initial statistical analysis similar to a significant wave height calculation is performed on the ADCP measurement data. First the ADCP data spectral analysis is determined and integrated for the frequency range corresponding to ocean waves, \(m_0=\sum \limits _{f_{l}}^{f_{u}} (S(f)d(f))\), while accounting for the noise as described previously. This is shown in Fig. 15 in linear scale. Most of the energy in the spectrum is contained in the period range of ocean waves. \(4.0\sqrt{m_0}\) is then computed as approximately equal to the average highest one-third of the current measurement fluctuations. This calculation is performed bin by bin to determine the profile of ‘significant’ horizontal current speeds as shown in Fig. 16. A few results at the upper bins could not be resolved due to the previously described data quality issues. Wave height and period data were also measured during the observations. Using linear theory to compute the wave-induced velocity, \(\omega a \frac{\cosh (k(z+h))}{\sinh (kh)}\), at the surface based on the measured significant wave height and period data, we can approximate a corresponding velocity profile. Here we use \(a=0.5 H_{1/3}\), \(\omega =\frac{2\pi }{T_0}\), and the dispersion relationship, \(\omega =\sqrt{g k \tanh (kh)}\), to determine k. These results are plotted alongside the ADCP-based profile. The comparison of these two profiles shows they are quite similar.

Fig. 15
figure 15

Spectral analysis of ADCP data for Bin 20 Ensemble 7

Full size image
Fig. 16
figure 16

Comparison of significant horizontal velocity profile of field measurements and a linear theory analysis from significant wave height and period data

Full size image

4 Conclusion

The objective of this engineering analysis was to gain an understanding of the turbulence characteristics of the Kuroshio Current flow near Kuchinoshima Island. A Signature 500 ADCP was deployed for approximately 24-h to measure velocity throughout the water column. The environmental conditions during the observations were ordinary. Thus, the applicability of the results can be considered generally applicable and repeatable; however, it is supposed that there are site-specific characteristics of the flow at other sites. The approach to handle noise issues and turbulence intensity results likewise are generally applicable to other sites for ocean current turbines. The findings from the analysis can be useful to the designers of the ongoing current turbine project in this area for use in performance and load prediction simulations.

The intermediate-frequency range (\(10^{-3}>f>1\) Hz) was investigated to understand which frequencies and their sources to account for with respect to the structural design of the current turbine. Spectral analysis of flow speed throughout the water column shows exponential decay in the inertial range, a peak due to wave effects, and noise saturation at higher frequencies. These are the important characteristics that arise in the intermediate-frequency range for which the ocean current turbine designer should account for. Average decay rates of \(f^{-1.35}\) and \(f^{-1.53}\) are computed for the ADCP and ADV data, respectively. This is a slight deviation from the theoretical \(f^{-5/3}\). While the limits of the inertial subrange are not clearly defined, our analysis does not capture the low-frequency side of the range. This along with wave effects and noise influence on the high-frequency side can possibly explain the deviation from the theory. In addition, noise floor issues partially attributable to the high water clarity arose at the higher end of the intermediate-frequency range. The higher frequency ADV instruments may provide better spectral information in this case.

Additionally, a method to correct for Doppler noise inherent to ADCP devices was implemented which was useful for the turbulence characterization analysis. Upon this correction, the average turbulence intensity over a large portion of the water column was approximately 10%. The integral time and length scales were calculated for a high speed flow time duration and seen to fluctuate substantially. Maximum values during high flow speed–time intervals of interest were found to be 10.70 s and 6.41 m, respectively. Finally, a comparison of ‘significant’ horizontal velocity data suggests the peak in the velocity spectrums is related to the wave effects.