A method to correct shallow-water model tests for tank wall effects

Abstract

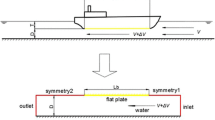
A new method is proposed to correct shallow-water model resistance tests for the effect of the tank side walls, i.e. to correct the resistance curve towards shallow water of infinite width. From computed flow fields along ships in shallow water and channels, the tank or channel walls are found to increase the overspeed along the ship (return flow) by an amount that is roughly constant over the channel section. An algebraic equation is derived from which this amount can be solved, using a volume flux derived from a single potential-flow computation. The effect of the tank walls on the resistance curve is represented by a speed shift corresponding with this overspeed. The assumptions made are checked against computed flow fields and resistances. The overspeed increment is very well predicted; its effect on the resistance is fairly well estimated as long as it is not too strong. The method, in routine use for shallow-water tests at MARIN, is most practical; and in view of the large tank wall effects in shallow water, it is essential for good predictions.

Appendix: Derivation of equation for overspeed increment in a channel

The cross section available to the flow at the midship location is determined by the nominal channel cross section A_C, minus the ship’s nominal midship sectional area A_M = β A_C, minus the area reduction due to the drop of the water level Δh, minus the effect of the dynamic sinkage of the vessel:

$$A_{{_{{\text{C}}}}}^{*}={A_{\text{C}}}(1 - \beta ) - 2\int\limits_{{B/2}}^{{b/2}} {\Delta h(y){\text{d}}y - B\sigma } .$$

1.1 Shallow, infinitely wide water

The overspeed ratio is $\gamma =\gamma (y,z)$. The volume flux through the area inside the channel wall locations at the midship section, is:

$${Q_{{\text{in}}}}{\text{/}}V=\int\limits_{{ - b/2}}^{{b/2}} {{\text{d}}y\int\limits_{{ - h}}^{{ - \Delta {h_{{\text{shallow}}}}}} {\gamma (y,z)} {\text{d}}z - {A_{\text{C}}}\beta \gamma (0,0)} .$$

(18)

The last term is the volume flux lost due to the midship sectional area of the hull multiplied by the local flow speed. The sinkage of the vessel is supposed to be in agreement with the local flow speed at the midship section, and is, therefore, absorbed in the integral.

1.2 Shallow channel

For this case, a larger flux (increased by Q_out) needs to pass by the area inside the channel walls, but also the resulting larger overspeed causes a further drop of the water level and increased sinkage. The additional overspeed $\Delta \gamma =\Delta {u_{{\text{channel}}}}{\text{/}}V$ is supposed to be uniformly distributed, Eq. 7. If again we suppose the increased sinkage of the vessel to correspond with the local overspeed, we can write the volume flux through the channel:

$${Q_{{\text{channel}}}}{\text{/}}V=\int\limits_{{ - b/2}}^{{b/2}} {{\text{d}}y\int\limits_{{ - h}}^{{ - \Delta {h_{{\text{channel}}}}}} {(\gamma (y,z)+\Delta \gamma )} {\text{d}}z - {A_{\text{C}}}\beta (\gamma (0,0)} +\Delta \gamma ).$$

(19)

The difference between the flux through the channel, and that through the same area for shallow water, then is:

$$\begin{aligned} ({Q_{{\text{channel}}}} - {Q_{in}})/V & = - {A_{\text{C}}}\beta \Delta \gamma +\int\limits_{{ - b/2}}^{{b/2}} {{\text{d}}y(h - \Delta {h_{{\text{channel}}}}(y))} \Delta \gamma - \int\limits_{{ - b/2}}^{{b/2}} {\gamma (y,0)(} \Delta {h_{{\text{channel}}}}(y) - \Delta {h_{{\text{shallow}}}}(y)){\text{d}}y \\ & ={A_{\text{C}}}(1 - \beta )\Delta \gamma +\frac{1}{2}Fr_{{\text{h}}}^{2}h\int\limits_{{ - b/2}}^{{b/2}} {\Delta \gamma \left[ {1 - \gamma {{(y,0)}^2} - 2\gamma (y,0)\Delta \gamma - \Delta {\gamma ^2}} \right]{\text{d}}y} - \frac{1}{2}Fr_{{\text{h}}}^{2}h\int\limits_{{ - b/2}}^{{b/2}} {\gamma (y,0)\left[ {2\gamma (y,0)\Delta \gamma +\Delta {\gamma ^2}} \right]} {\text{d}}y \\ & ={A_{\text{C}}}(1 - \beta )\Delta \gamma +\frac{1}{2}Fr_{{\text{h}}}^{2}h\Delta \gamma \int\limits_{{ - b/2}}^{{b/2}} {(1 - 3} \gamma {(y,0)^2}){\text{d}}y - \frac{3}{2}Fr_{{\text{h}}}^{2}hb\bar {\gamma } \cdot \Delta {\gamma ^2} - \frac{1}{2}Fr_{{\text{h}}}^{2}bh\Delta {\gamma ^3} \\ \end{aligned}$$

(20)

where $\bar {\gamma }$ is the mean overspeed at the water surface over the channel width, in shallow water. We notice a term quadratic in $\gamma (y,0)$ that would prevent a further simplification. However, as the overspeed ratio in typical cases is just somewhat larger than 1 and decreases gradually to 1 over a distance larger than the typical channel width, we approximate it by the square of the mean overspeed.

This difference of the volume flux equals the excess volume flux passing outside the channel wall locations for the shallow-water case:

$${Q_{{\text{channel}}}} - {Q_{{\text{in}}}}={Q_{{\text{out}}}}.$$

(21)

Substituting and dividing by A_C we arrive at the following third-degree equation for ∆γ:

$$\Delta \gamma \left( {1 - \beta +\frac{1}{2}Fr_{{\text{h}}}^{2}(1 - 3{{\bar {\gamma }}^2} - 3\bar {\gamma } \cdot \Delta \gamma - \Delta {\gamma ^2})} \right)=\frac{{{Q_{{\text{out}}}}}}{{V \cdot {A_{\text{C}}}}}.$$

(22)