Abstract
In this paper, we introduced an intermittent wave energy generator (IWEG) system with hydraulic power take-off (PTO) including accumulator storage parts. To convert unsteady wave energy into intermittent but stable electrical output power, theoretical models, including wave energy capture, hydraulic energy storage, and torque balance between hydraulic motor and electrical generator, have been developed. Then, the integrated IWEG simulator was constructed and tested at the Ningbo Institute of Technology. Through a series of experimental tests, the relationship between operating flow rates and pressure drops across the hydraulic motor was established. Furthermore, on the basis of the pressure drop signal, we proposed a feedback control method on the basis of the pressure drop database as the feedback control signal to eliminate the disturbance of periodic peak pressure impulse through the regulation of the opening ratio of a proportional flow valve and achieved the effective and stable electric power output, albeit intermittently. Compared with the previous complex control theories and algorithms, this method can keep the power output more stable over a wide range of operating conditions. Furthermore, experimental tests indicate that the IWEG system, with hydraulic PTO, including hydraulic accumulator and proportional flow control valve, is simple, reliable, and easy to control. Most importantly, the real-time power output is stable, and power quality and generation efficiency are significantly improved.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, sustainable energy generation has become increasingly important because of the current limitations of the conventional energy resources and the drive to reduce pollution [1]. Thus, ocean wave energy, a renewable energy resource widely distributed in the world, has intrigued people for centuries. Many devices have been developed for wave energy conversion (wave energy converters—WECs), and numerous wave energy generation systems have emerged [2]. There are four types of WECs classified according to their operating principles. The first one is the overtopping device, such as the Wave Dragon and the Tapchan, which utilizes the potential energy of the water stored in the water reservoir. The second one is the oscillating water column (OWC), which depends on the water column and the pressure difference generated by waves [3]. The third one is the hinged contour device, such as the Pelamis, which unfortunately has been forced into administration in 2014. The fourth one is oscillating buoyant floating/moored bodies device, such as the Archimedes Wave Swing (AWS), which has gained attention in recent years [2, 4,5,6]. In addition, devices with different principles may require different power take-off (PTO) systems:
-
The overtopping device often uses the hydro turbine that drives the rotating generator.
-
The oscillating water column often uses the air turbine that drives the rotating generator.
-
The hinged contour device often uses the hydraulic power take-off system.
-
The buoyant moored device often uses the linear generator system.
The wave energy is intermittent and random, and the velocity of it is low. In addition, wave impact forces are huge (the peak value can be about 7–10 times greater than the average one). Thus, the generated power is typically oscillatory with large impulse peaks [7]. To reduce the power oscillations, systems with additional energy storage devices, such as flywheels, hydraulic accumulator, superconducting magnetic energy storage, super capacitors, and batteries, have been proposed as parts of WECs.
Many efforts have been devoted to the study of WEC control. Initially, to explain that the resonance occurs when the wave excitation force becomes in phase with the velocity of floating body, the control of point absorbers was focused on the maximum energy transfer. Strategies, such as latching control, were introduced [8]. Then, researchers deployed advanced AI and heuristic control techniques, such as genetic algorithm (GA) and artificial neural networks (ANNs), to optimize the energy capture of WECs [9]. Fuzzy logic-based controllers have also featured in the research [10]. Model predictive control (MPC) has drawn attention as a potential optimal controller for WECs. However, most of these control methods are computationally expensive, heavily dependent on the system mathematical model and difficult to realize the real-time control. Stable and smooth power output becomes very difficult, because wave energy is intermittent and the excitation amplitude is oscillating and variable. This results in an unstable WEC system, especially a single floating buoy [11]. WEC systems with hydraulic circuits for PTO are composed of many components including, but not limited to, energy accumulator, hydraulic motor, electrical generator, pressure regulating valve, safety valve, reversing valve, and manifold blocks. Most components are non-linear and have their own real-time, dynamic hydraulic parameters, meaning that it is impossible to establish accurate theoretical models.
For floating-buoy-type WECs, if wave energy is converted into the stable and continuous electric supply, there are two methods of energy storage. One is the ‘direct-drive’ power generation, which mainly utilizes gear systems and flywheels for energy storage [12], and the other is the hydraulic energy storage. Hydraulic energy storage can dampen the impact of wave impulses, because the hydraulic accumulator has much higher buffering and energy storage capacities [13, 14] than the direct-drive mechanical transmission. In addition, gear systems and flywheels can be easily damaged or even destroyed by extreme waves. When hydraulic accumulator pressure reaches a certain threshold, the outlet valve of the accumulator opens, and the hydraulic motor PTO will start to work. Although the electrical power from a single point absorber WEC cannot last for a long time because of intermittent wave energy supply, but we can keep output power on stable in several minutes or even hours [15], which is the main reason for the design of intermittent wave energy generator (IWEG) system presented in this paper.
Here, “Stable” mainly contains the following meanings:
-
1.
When the IWEG system captures enough wave energy and reaches the set point, the generator began to produce stable electrical energy.
-
2.
When wave energy is not enough, the accumulator will drive power generation for some minutes or even hours and then stop working. However, the electrical energy during this time is stable.
-
3.
For single floating buoy, the IWEG system can always achieve stable electrical energy regardless of the real-time change of wave energy.
-
4.
The more the number of floating buoys, the more stable the electrical energy produced by the system.
The outlet valve of the hydraulic accumulator opens when the PTO of the IWEG system works. When the valve pressure is fixed, the flow rate of the hydraulic oil will decrease rapidly, resulting in the oscillating output power and the substantial decrease in the efficiency of it if there are no controls. However, if the pressure and flow rate of the hydraulic oil can be regulated by the valve is open to a certain degree in a controllable way, energy input from oscillating waves with variable amplitudes will still be able to produce the stable and good quality power output. That means control strategies to adjust and stabilize the electrical output power must be developed and implemented using the IWEG system. In this paper, to obtain the stable power output, the design and development of the IWEG system with hydraulic energy storage and pressure drop feedback control were presented. In addition, results about physical testing of the constructed IWEG simulator were also presented. The control signal based on a motor pressure drop database was experimentally obtained from the IWEG system.
2 Working principle of the IWEG system
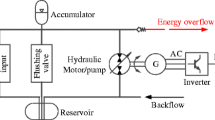
To capture wave and current energy, a catamaran-type floating platform was designed and built by NIT, which was deployed in the East China Sea near Ningbo city. Because most ocean energy generation systems can be easily destroyed by heavy seas, the platform can be towed back to avoid severe sea conditions. The floating test platform includes the floating buoy and linking parts, the hydraulic energy conversion and transmission parts, the hydraulic energy storage part, electric generation and control parts, the marine current energy conversion device, and the platform (Fig. 1). The working principle of IWEG system for wave energy generation is shown in Fig. 2. As the key WEC parts, a certain buoy type has its own character because of different ocean environments, different wave energy capture methods, and different structural platforms, and it is hard to determine which buoy type is the best. Typically, the cylindrical buoy has the merits of high wave energy capture efficiency and the conical buoy has the merits of well suitability. Combined the two merits and structural character, the novel buoy is adopted in the floating platform. The buoy has cylindrical body and a cone-shaped bottom, as shown in Figs. 1(4) and 2(13). When the floating buoys oscillate up and down around the axis under wave loads, piston pumps will remove low-pressure hydraulic oil from the oil tank and pump high-pressure hydraulic oil to the accumulator. First, oscillating wave energy is converted into the high-pressure hydraulic oil supply, which is stored in the hydraulic accumulator. When the oil pressure reaches a certain threshold, through a proportional flow control valve is opened, the high-pressure oil will be released from the accumulator to the hydraulic motor to drive the electric generator, which will rotate at a near-constant speed. If the hydraulic oil pressure drops to a certain low value, the proportional valve will be closed. Thus, wave energy inputs will be conserved in the accumulator cyclically. Then, the cycle of converting the continuous wave energy input into the stable electrical output is completed, albeit intermittently.
Schematic diagram of the system for intermittent wave energy generation with hydraulic energy storage and pressure control. (1) Piston pump, (2) one-way valve manifold, (3) accumulator, (4) pressure sensor, (5) two-way electro-hydraulic proportional flow control valve, (6) solenoid valve, (7) flow sensor, (8) hydraulic motor, (9) electrical generator, (10) load, (11) oil filter, (12) Oil tank; (13) floating buoy
The schematic diagram of the IWEG system consists of the following sub-systems: wave energy capture, hydraulic energy storage, electrical generation, and control (Fig. 2). The wave energy capture sub-system includes oscillation buoys and piston pumps to convert mechanical energy into hydraulic energy. Four check valves are used to establish a hydraulic bridge circuit, which is used to convert the two opposite hydraulic oil flows into a single direction supply. The hydraulic energy storage sub-system mainly consists of the accumulator, the unloading circuit, the pressure instruments, and flow meter sensors. The electrical generation sub-system consists of the hydraulic motor and electrical generator. The electrical control sub-system includes the pressure sensor, the flow meter, and the proportional flow control valve, which is used to regulate the pressure drop and the flow rate of hydraulic oil through the motor. These sub-systems are configured as two closed-loop operations. One consists of the wave energy capture and hydraulic energy storage, and the other being the hydraulic power take-off for electrical power output is comprised of the energy supply/storage, hydraulic motor, electrical generator, pressure feedback flow rate controller, and the applied load.
3 The theoretical model
In general, methods to control a WEC system include pump displacement control, tension adjustment control, and ballast weight control. Pump displacement control method is to stabilize the generator speed through adjust pump displacement, tension adjustment control method is to stabilize the electric power through adjust loads, and ballast weight control method is to improve the quality of electric power by rectification and ballast. In fact, because the frequency of wave energy is intermittent and variable, it is difficult to take off power continuously and unable to produce stable electricity when WEC works [4]. However, PTO for stable electricity output over a short-time scale (for example, several minutes to hours cyclically) is possible. To improve the quality and efficiency of electrical power generation systems, maintaining a stable flow rate of hydraulic oil is necessary.
The ocean wave fluctuation is caused by wave excitation with different frequencies and amplitudes. In this paper, only the wave fluctuation caused by a single frequency excitation in heave is considered for simplicity. In most case, wave can be simplified as regular and be presented as
where x (m) is the trajectory of the water particle in vertical direction; \({A_0}\) is the amplitude of wave; and \(\omega\) is the circular wave frequency, respectively.
In this paper, the IWEG can be considered as a simple floating-buoy device, semi-submerged with a cylindrical shape in the equilibrium position, of which the heaving displacement can be represented by [16]:
where \({F_0}\) is the wave force amplitude; t (s) is time; \(\gamma\) is the phase angle that depends on the wave force components; \({Z_0}\) is the amplitude of floating buoy; \({\sigma _Z}\) is the phase angle that depends primarily on the dimensionless system damping factor \({\Delta _z}\); \(~{\omega _z}\) is the natural circular heaving frequency \(\left( {{\omega _z}=\sqrt {\frac{{\rho g{A_{{\text{wp}}}}}}{{m+{m_\omega }}}} } \right)\); \({A_{{\text{wp}}}}\) is the waterplane area of the buoy; \(\rho\) is seawater density; \({m_\omega }\) is the added mass (i.e., the mass of the water excited by the heaving motion); and \(m\) is the mass of the buoy.
A sketch of the closed-loop of wave energy capture and storage sub-system is shown in Fig. 3, in which the floating buoy is connected kinetically with the piston pump. A double-acting hydraulic cylinder pump is used in the IWEG system, with one of the ports linked directly to the buoy, and another port hinge jointed with the piston pump. It is assumed that the heaving displacement of the buoy in the vertical direction equals the swinging of the link. On the basis of the principle of moment balance, when the buoy moves in the vertical direction, the force acting on the piston pump (\({F_1}\)) is
where \({p_1}\) is the oil pressure in the piston pump; \(~{L_1}\) is the length of the lever arm between the base center and the buoy; \({L_2}\) is the length of the lever arm between the piston pump shaft and the base; and D is the inner diameter of the piston pump. The direction of \({F_1}\) is opposite to that of \({F_0},\) so the modified heaving displacement of the buoy is
On the basis of lever principle (assuming rigid body), the distance moved by the piston pump (\({z_1}\)) is \({z_1}=\frac{{{L_2}}}{{{L_1}}}z\). Thus, the following expression is obtained:
In one heaving cycle, the piston pump removes low-pressure oil and pumps high-pressure oil twice, and the effective capacity of it can be calculated as
where d is the diameter of the piston rod; and \({\eta _Q}\) is the coefficient of hydrodynamic losses including leakage.
As shown in Eqs. 3, 5, and 6, with a floating-buoy oscillating up and down in a given wave period, the oil pressure in the hydraulic circuit (\({p_1}\)) rises, which leads to an increase in the \({F_1}\) in the next heaving period and a corresponding decrease in \({z_1}.\) It means that the motion amplitude of the buoy is damped because of the PTO during the period of wave energy capture and hydraulic energy storage.
The hydraulic PTO circuit loop of the IWEG system, including the electric power generation and control, mainly consists of accumulator, proportional flow control valve, hydraulic motor, electrical generator, and the resistive load (Fig. 4). p 1, p 1a, and p 1b are the inlet pressure, inner pressure, and outlet pressure of the accumulator, respectively. p 2, A, q, and ω are the inlet pressure of the hydraulic motor, the opening area of the proportional valve, the valve flow rate, and the speed of the electrical generator, respectively. Symbols R and E represent the resistive load and the circuit voltage of the generator, respectively. To ensure generator works with high efficiency, the circuit voltage needs to be kept stable within its rated range.
When the electro-hydraulic motor and generator rotate, the generator rotor coil and the resistive load constitute a sub-loop, in which the electric current flows through the load correspondingly. Thus, the electromagnetic resistive torque (T) will act on the rotor coil. If it equals the output torque of the hydraulic motor, the rotational speed of the electrical generator will maintain a steady value, and the load voltage will be steady, as expected. The electromagnetic resistive torque (T) is expressed as [17]
where R is the load resistance; r 0 is the inner circuit resistance; \(\omega\) is the rotation speed; and K is the number of rotor poles.
The output torque (M) for the hydraulic motor is [15]
where V is the displacement of the hydraulic motor; \({p_2}\) is the inlet pressure of the motor; \({p_0}\) is the outlet pressure of the motor (generally, we set \({p_0}\) ≈ 0); \(\Delta p\) is the pressure drop between inlet and outlet (\(\Delta p={p_2} - {p_0}={p_2}\)); and \({\eta _m}\) is the efficiency of the motor.
If the rotation speed of the generator is steady and the outlet torque (M) is equal to the electromagnetic resistive torque (T), combining Eqs. 1 and 2, we can obtain the inlet pressure of the motor:
As shown in Eq. 3, relationships among all the parameters above are dynamic, interdependent, and coupled. To maintain that the speed of hydraulic motor is constant, it is necessary to adjust the opening area of the proportional valve and control the flow rate (q). For the proportional valve, the flow vs pressure characteristics (i.e., a relationship between flow and pressure) is influenced by the pressure differential across two ports, the opening area of the proportional valve, and its shape. Considering an opening shape, which is similar to a thin-walled and elongated orifice, the flow-pressure characteristics can be expressed as
where q is the flow rate of the throttle; \({C_d}\) is flow discharge coefficient of the port; A is the opening area of the valve; \(\rho\) is oil density; and m is the throttle correction factor (m = 0.5–1).
If the electromagnetic load torque applied on the electrical generator equals the output torque of the hydraulic motor, the rotational speed (\(\omega\)) of the electrical generator will be steady, and the same principle can be applied to the flow rate (q). It is vital for achieving the stabilization of the electrical voltage. In Eq. 4, when the pressure drop (∆p) decreases, we can increase the opening area (A) to keep the flow rate (q) stable.
4 Control method of PDDFC
In this paper, to stabilize the electrical power output to a specific range, a control method was proposed on the basis of the pressure drop database as the feedback control signal (PDDFC). The method of PDDFC is generally described as: on the basis of real-time pressure drop with the experimental pressure drop and the flow rate (∆p vs q) database be constructed, we adjust the opening ratio (\({k_{\text{o}}}\)) of the proportional valve through controller. Then, the flow rate of the motor is maintained within a particular range, and the output power is stabilized correspondingly.
Under the action of floating buoy, high-pressure hydraulic oil is reserved in the hydraulic accumulator. When oil pressure in the accumulator reaches a certain high value (\({p_{{\text{open}}}}\)), the proportional valve will be opened and high-pressure oil will be released, which results in that the hydraulic motor and power generator rotate with high speed. When the oil pressure decreases to a certain low value (\({p_{{\text{close}}}}\)), the proportional valve will be closed, and the wave energy will be reserved in the accumulator repeatedly.
On the basis of the mathematical model above, several observations deserve to be pointed out: First, during a wave energy capture half cycle, the storage pressure in the accumulator (\({p_{1b}}\)) rises nonlinearly, and the periodic wave force peaks produce periodic storage pressure impulses, which means that it is not easy to obtain the opening pressure value of the accumulator. Second, because the inlet port pressure of the proportional valve (\({p_{1a}}\)) equals the outlet pressure of the accumulator, and the outlet port pressure of the valve equals the inlet pressure of hydraulic motor (\({p_2}\)), it is sufficient to just sample pressure data of \({p_1}\), \({p_{1a}}\), and \({p_2}\). Thirdly, during the hydraulic motor rotation half cycle, the floating buoy is still oscillating, which continuously produces periodical pressure impulse signals. Thus, how to judge the cracking and shut-off pressure signals and eliminate the pressure pulse influence are crucial. Finally, to ensure that the output power of the generator is steady within a certain range, we need to stabilize the flow rate of the hydraulic motor mainly through adjusting the opening ratio of the proportional valve (Fig. 5).
The control strategy, as shown in Fig. 6, has the procedure defined as following steps:
Preparation: obtain the pressure drop data (\(\Delta p\)) with different flow rates (q) by starting the wave energy capture and hydraulic energy storage processes and obtain raw data, while the system reaches an initial steady state.
Step 1 Record real-time inlet pressure (\({p_1}\)) of the accumulator, and the sampling frequency is n = (8–10) per wave period (T).
Step 2 Calculate the average pressure value. The inlet pressure data include the accumulator pressure and pressure impulse of the piston pump. The pressure impulse peak may be far greater than the opening pressure value under the action of regular/irregular waves. To eliminate the pressure impulse of the piston pump, the average pressure value is calculated over a complete wave period, which is as follows:
Step 3 Set the opening pressure of the accumulator to \({p_{{\text{open}}}}\), and compare it with \({\bar {p}_1}\). If the average pressure is higher than the opening pressure, i.e., \({\bar {p}_1}\) > \({p_{{\text{open}}}}\), the process will proceed to the next step. Otherwise, it will return to Step 1.
Step 4 Open the proportional valve and release the high-pressure hydraulic oil. The hydraulic motor will rotate at a set speed. Then, the electrical generator will start to work.
Step 5 In this step, the inlet pressure (\({p_2}\)) and the flow rate (\(q\)) of the hydraulic motor are recorded in real-time. Considering that the motor outlet is directly connected to the returning tank, we can set \({p_0}=0\). Thus, \(\Delta p={p_2} - {p_0}={p_2}\). Similar to Step 2, to eliminate the periodic pressure impulse of the piston pump, the calculation equation of the average inlet pressure of the motor is expressed as
Combining the real-time pressure drop with the experimental pressure drop and the flow rate (\(\Delta p~{\text{vs}}~q\)) database, the setting point of the opening ratio for the proportional valve is obtained. Then, the flow rate of the motor is maintained within a particular range, and the output power is stabilized correspondingly.
Step 6 Record the inlet pressure (\({\bar {p}_2}\)) and the flow rate (\(q\)) of the hydraulic motor within a wave period in real time, and obtain the average hydraulic power value of \({\bar {p}_2} \times q\); set the valve closing power to \({p_2}{q_{{\text{close}}}}\), and compare it with the average hydraulic power. If the average power value is less than the set valve closing power value, i.e., \({\bar {p}_2}q\) < \({p_2}{q_{{\text{close}}}}\), the process will proceed to the next step; otherwise, the process will return to the Step 5.
Step 7 On the basis of the criterion of \({\bar {p}_2}q\) < \({p_2}{q_{{\text{close}}}}\), the proportional valve remains closed, and the wave energy is stored in the accumulator again during the rest of the cycle. Then, the energy storage-electrical power generation cycle is repeated.
In addition, when the amplitude of the wave input decreases to a certain low value, sensors will detect the signals and power generation will stop completely.
From the above description for the method of PDDFC, compared with typical control methods such as AI, GA, MPC, and ANNs, this control method has the following advantages
-
It is simple, and the control method adjusts the opening ratio only according to the pressure drop to realize the stability of the output power. Accordingly, the computation time is relatively small and the response time is fast. It is easy to realize real-time control.
-
The database of pressure drops and opening ratio of proportional valve are established by preliminary experiment, which makes the control method more reliable and close to engineering practice.
-
It is suitable for different wave conditions including regular wave and irregular wave situations, and the control method can achieve stable output power by calculating the average pressure.
5 Experimental tests, results, and analysis
5.1 Test rig description
Figure 7 shows the IWEG test rig simulator constructed in the Ocean Energy Lab at NIT. The main components are as follows: (1) is the power pack with directional control four-way valve, of which the rated power is 7 kW, and the system maximum operating pressure is 32 MPa. The power pack replaces the wave energy capture part (i.e., the floating buoy and the piston pump). The wave frequency and the amplitude of the buoy are simulated by adjusting the reversing time of four-way valve and the pump oil, respectively. Directional four-way check valve can control the periodically varying oil flow, which simulates the reciprocating motion of the piston pump into a uni-directional oil supply. (2) and (3) are the hydraulic pressure and flow sensors, respectively. (4) is the fixed displacement hydraulic vane motor with a capacity of 12 mL/rev. (5) is the electrical generator, directly driven by the hydraulic motor through coupling. The generator is of a single-phase synchronous design (Type ST-3K), rated at a voltage of 220 V and a rational speed of 1500 rev/min. (6) is the oil tank with a capacity of 200 L. (7) is the hydraulic accumulator with a rated capacity of 63 L, the maximum pressure limit is 32 MPa. At the inlet of the accumulator, an overflow pressure relief valve is set at a pressure of 25 MPa to ensure the safety of IWEG operation. (8) is the electro-hydraulic proportional flow control valve, which is controlled by a PLC controller (9) and used to stabilize the flow rate of the hydraulic motor through adjusting the opening ratio of the control valve. For energy dissipation, lamps and adjustable resistors were adopted as the applied loads (10).
On the basis of parameters of the motor and generator above, when considering factors, such as bias and lags while keeping the electrical generator steady, the design flow rate of motor is calculated to be around 18 L/min. In the experiment, the cracking pressure of the accumulator is set to 20 MPa. Then, the opening ratio of proportional valve is adjusted. Signals, such as the outlet pressure of the accumulator, the inlet pressure, and the flow rate of the hydraulic motor, are sampled through the pressure and flow sensors. All analog signals were written into the PLC program and were converted into digital signals. In addition, to record real-time pressure and flow rate signals, the communications between object linking and embedding for process control (OPC) and PLC were established through the LabVIEW software.
5.2 Construction of the control signal database
To stabilize the flow rate of the hydraulic motor, the first step is to construct experimental database of \(\Delta p - q - {k_{\text{o}}}\). For each experimental test, the valve-opening ratio (\({k_{\text{o}}}\)) was fixed, and the real-time pressure drop (\(\Delta p\)) and flow rate (q) data were recorded. We selected the pressure drop point when the flow rate value reaches 18 L/min, and recorded the data of \(\Delta p - {k_{\text{o}}}\). We changed the opening ratio and repeated the experiment above. In addition, the opening ratio of the valve was adjusted from 0.3 to 1.0 step by step, and the complete database of \(\Delta p - {k_{\text{o}}}\), in the form of seven hydraulic motor flow rate curves with different opening ratios shown in Fig. 8, was constructed. Then, all data were written into the PLC program, which is used to control the opening ratio of the proportional flow control valve. As shown in Fig. 8, a decrease in the pressure drop between the outlet of accumulator and the inlet of motor for a fixed valve opening leads to a corresponding decrease in the motor flow rate. To ensure the flow rate of motor steady for a given opening ratio of the valve, i.e., around the 18 L/min (the horizontal line in the curve), we set the X-coordinate as the pressure drop value at each corresponding intersection point of two lines. Horizontal lines with flow rates of 17, 16, and 15 L/min were drawn, which were compared with pressure drops obtained from the same way, respectively. On the basis of the curves in Fig. 8, the corresponding database of pressure drops and opening ratios with these flow rates is presented in Table 1. When the pressure drops decrease, the opening ratio increases nonlinearly. Furthermore, we constructed the control database for the opening ratio under discretized pressure drop signal for feedback (Table 2). Additional data were obtained through linear interpolation, and the minimum opening ratio is 30%. When the opening ratio is less than 30%, the driving force will be small, which will not be able to overcome the starting torque of the coupled motor and electrical generator. Thus, the power generation will not take place until the flow rate becomes large enough.
5.3 Power stabilization test results
When the power pack works, high-pressure oil is pumped and stored in the accumulator. To simulate reciprocating motion of piston pump, directional control four-way valve with change directions for each period was used in test rig. Here, wave period is set to 4 s. Two oil charge pressure curves of the accumulator are shown in Fig. 9: 1 is the pressure curve without changing direction and 2 is the pressure curve with direction changed by the four-way check valve. In Curve 1, pressure rises steadily without any oscillation, and the theoretical cracking pressure value is set to 20 MPa, and during tests, the recorded value of cracking pressure reaches 20.2 MPa. In Curve 2, because the oil flow periodically change direction, the pressure in the accumulator increases, but varies within a small range. With the increase in oil pressure, the oscillation amplitudes decrease steadily. In this curve, the cracking pressure reaches the 23.4 MPa, and the average cracking pressure calculated through Eq. 11 is 20.6 MPa. The oil charge times are 574 and 768 s for Curve 1 (without changing direction) and Curve 2 (with direction changed by the four-way check valve), respectively. It indicates that the oil charge time is delayed and longer because of the periodical change in oil direction.
When analog signals of pressure drop (\(\Delta p={p_2} - {p_0}={p_2}\)) and flow rate (\(q\)) were converted into digital signals in PLC, the control signal used for the opening ratio of the valve was determined through the database. Furthermore, the digital signal for the opening ratio was converted back into an analog signal to drive the proportional flow control valve, which is used to keep the voltage and output power of the motor steady within a range.
To obtain the optimal flow rate of the hydraulic motor, experimental tests without wave energy capture (i.e., inlet valve of the accumulator is closed with discount of peak pressure impulse from direction change for piston pump) have been done, and the curves of output power are shown in Fig. 10. There are four curves of output power with flow rates of 18, 17, 16, and 15 L/min, and the average power outputs are 2.4, 2.0, 1.7, and 1.6 kW, respectively. The lasting time for each corresponding flow rate is 225, 250, 295, and 310 s, and the total electrical energy output is 540, 500, 501.5, and 496 kJ, respectively. In addition, the output power curve with a fixed 60% opening ratio of proportional valve was also drawn for comparison. The output power diminishes rapidly in less than 3 min; however, the time that the voltage is kept within the rated ranges (i.e., 200–240 V) is only 20 s. This illustrates several points. First, the power quality of the generation system is poor without proportional valve control. Second, the real-time adjusting of opening ratio control method with pressure drop database signal feedback can be used to stabilize the output power effectively. Third, the optimal flow rate is about 18 L/min, at which the generator efficiency is the highest among all flow rates, which is consistent with the rated flow of the hydraulic motor.
Figure 11 depicts two output power curves for the IWEG system with optimal rated flow rate set at 18 L/min. Curve 1 shows the output power when only the accumulator is working, and Curve 2 is the output power when both accumulator and piston pump are working. It illustrates that both curves are stable within a range, and the lasting time for stable output power in Curve 2 is 60 s longer than that of in Curve 1. Figure 12 is a supplement to curve 2 of Fig. 11, which shows the output power curve during the final 20 s before turning off the proportional valve, and the output power does contain impulses at a period half of the wave frequency.
To maintain a cyclic and continuous operation of the IWEG system, i.e., the simulator can capture wave energy input continuously, the high-pressure oil accumulator is charged constantly, and the decoupling of the PTO from the energy capture would allow the high-pressure oil discharges through driving the motor to generate electricity stably and periodically. The output power curve for three consecutive cycles is shown in Fig. 13. The period for electricity generation is about 290–310 s, and the output power agrees well with Curve 2 in Fig. 11, while the lasting time for energy storage interval is about 400–440 s and the system is stable. For comparison, the power output curve of a fixed control valve-opening ratio of 30% is shown in Fig. 14, and the electricity generation could be initially maintained to last about 390 s with an average power of 1.4–1.6 kW, but the whole system becomes unstable. The instantaneous power output is only about 0.2 kW with an intermittent time of 10–15 s, even the IWEG continuously absorbs wave energy input. This is because that the hydraulic oil pressure is too low to drive the motor continuously, resulting in a poor power quality, low efficiency, and unstable system for wave energy generation. By comparing Fig. 13 with Fig. 14, we can find that the output power curve with the proportional control of flow rate using pressure signal as feedback has a much better power quality and higher systems efficiencies. Thus, this control method is effective for stabilizing the output power.
6 Conclusions
In this paper, we presented an IWEG system with hydraulic power take-off (PTO), including accumulator storage parts. To convert unsteady wave energy into intermittent but stable electrical output power, theoretical models, including wave energy capture, hydraulic energy storage, and torque balance between hydraulic motor and electrical generator, have been developed. Then, the complete system of an integrated IWEG simulator was constructed and tested in a laboratory. A relationship between operating flow rates and pressure drops across the hydraulic motor was established through experimental tests. On the basis of the obtained pressure drop signal database, we proposed a feedback control method to eliminate the disturbing periodical peak pressure impulse through the regulation of the opening ratio of a proportional flow valve, and achieved an effective, stable, and steady electric power output for continuous wave energy capture, albeit intermittently. Compared with the previous complex control theories and algorithms, this method can keep the power output more stable over a wide range of operating conditions. Furthermore, through a series of experimental tests, it was demonstrated that the IWEG system with hydraulic PTO, including hydraulic accumulator and proportional flow control valve, is simple, reliable, and easy to control. Most significantly, the power output is stable, and the power quality and generation efficiency are improved. It is necessary to pointed out that the parameters in Table 2 can be used in real sea conditions. While if some parameters or structure of the test rig shown in Fig. 7 have changed, the new experimental test must be done to obtain the new Feedback control signal database table similar to Table 2. However, this investigation only aims at the IWEG with a single floating buoy. How to smooth output power for IWEG with a multi-floating-buoy array still needs to be further studied.
References
Truong DQ, Ahn KK (2012) Wave prediction based on a modified grey model MGM(1,1) for real-time control of wave energy converters in irregular waves. Renew Energy 43:242–255
Babarit A (2015) A database of capture width ratio of wave energy converters. Renew Energy 80:610–628
de Andres A, Guanche R, Vidal C, Losada IJ (2015) Adaptability of a generic wave energy converter to different climate conditions. Renew Energy 78:322–333
Ahn KK, Truong DQ, Tien HH, Yoon JI (2012) An innovative design of wave energy converter. Renew Energy 42:186–194
Wang Y-L (2015) Design of a cylindrical buoy for a wave energy converter. Ocean Eng 108:350–355
Jama MA, Noura H, Wahyudie A, Assi A (2015) Enhancing the performance of heaving wave energy converters using model-free control approach. Renew Energy 83:931–941
Soleimani K, Ketabdari MJ, Khorasani F (2015) Feasibility study on tidal and wave energy conversion in Iranian seas. Sustain Energy Technol Assess 11(9):77–86
Babarit A, Duclos G, Clement A (2010) Comparison of latching control strategies for a heaving wave energy device in random sea. J Appl Ocean Res 26:227–238
Valrio D, Mendesb M, Beirao P, Costa J (2008) Identification and control of the aws using neural network models. Appl Ocean Res 30:178–188
Schoen M, Hals J, Moan T (2011) Wave prediction and robust control of heaving wave energy devices for irregular waves. IEEE Trans Energy Convers 26:627–638
Alcorn R, O’Sullivan D (2013) Electrical design for ocean wave and tidal energy system. The Institution of Engineering and Technology, London, pp 111–129
Xiao X, Bai N, Kang Q et al (2014) A review of the development of wave power system and the research on direct-drive wave power system. Trans China Electro Tech Soc 29(3):1–11
Muhando EB, Senjyu T, Urasaki N et al (2007) Gain scheduling control of variable speed WTG under widely varying turbulence loading. Renew Energy 32(14):2407–2423
Jingwei BAO, Wei LI et al (2012) Analysis of an inverse pendulum wave power generation system with pressure-maintaining storage based on hydraulic transmission. Autom Electr Power Syst 36(14):205–208
Wang K, Tian L, Wang X et al (2014) Characteristics of power generation system with hydraulic energy—storage wave energy converter. J South China Univ Technol 42(6):25–30
McCormick ME (2013) Ocean wave energy conversation. Dover Publications, Inc, New York, pp 52–58
Abdin ES, Xu W (2000) Control design and dynamic performance analysis of a wind turbine-induction generator unit. IEEE Trans Energy Convers 15(1):91–96
Acknowledgements
The paper was supported by Zhejiang Natural Science Fund (LY13E090007), Ningbo Natural Science Fund (2016A610211), and Ningbo major scientific and technological projects (2012C10041 and 2017C110005), China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Song, R., Dai, Y.M. & Qian, X. Intermittent wave energy generation system with hydraulic energy storage and pressure control for stable power output. J Mar Sci Technol 23, 802–813 (2018). https://doi.org/10.1007/s00773-017-0512-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00773-017-0512-4