1 Introduction

When a ship navigates in a seaway, there are various sources of additional resistance including the wind, waves, and rudder angle compared with the resistance of an advancing ship in calm water. Therefore, it is important to obtain an accurate prediction of the added resistance when designing a ship’s propulsion power. Furthermore, to limit greenhouse gas emissions, the Marine Environment Protection Committee (MEPC) of the International Maritime Organization (IMO) has established regulations concerning the measurement of energy efficiency levels, such as the Energy Efficiency Design Index (EEDI). Of the various kinds of additional resistance components, the wave-induced added resistance has become an important topic in the fields of seakeeping and ship resistance [1, 2].

The added resistance at short wavelengths is another main interest in practical ship design because the wave energy is concentrated in a relatively short wavelength region as the lengths of modern ships increase. In the short wavelength region, the ship motion can be neglected and the diffraction component is dominant in the added resistance in waves [3]. Thus, the wave amplitude and bow shape significantly affect the added resistance in short waves. It is believed that highly nonlinear free-surface flows such as overturning and wave breaking around the ship bow will occur when the wave amplitude increases. In this situation, the variation of the bow shape above the mean water level should also be considered.

Even though many studies on wave-added resistance have been conducted based on experiments [4–7] and potential-flow solvers [8–11], computational fluid dynamics (CFD) has also been applied to simulate the added resistance in waves. In the CFD method, it is possible to investigate the details of flow characteristics such as pressure and velocity distribution, even for the violent free-surface flows that interact with a solid body. In addition, current numerical methods such as the volume-of-fluid (VOF) or level-set methods provide reliable results for violent free-surface problems in which the topology of the free-surface boundary is largely changed [12–15]. Furthermore, the CFD method can be utilized to study the added resistance in short waves of ships with different bow shapes above the still-water level.

For this scenario, various methods have been applied to investigate the effect of different bow shapes on the added resistance in short waves. Because ship motion can be neglected in the short wave condition, Faltinsen et al. [3] derived the asymptotic formula of the added resistance in short waves by assuming that the ship has a vertical side at the water plane, and that the wavelength is small compared to the draft of the ship. Guo and Steen [16] studied the added resistance in waves for different bow shapes of the KRISO’s very large crude oil carrier (KVLCC2), and they compared the experimental results with the asymptotic formula [3]. The discrepancy can be found for slender bow shapes because of the simple assumption of a velocity of the local steady flow. In another study, Fujii and Takahashi [4] also derived the semi-empirical formula of the added resistance in short waves by modifying several coefficients in the drift force of a fixed vertical cylinder. Then, the National Maritime Research Institute (NMRI) in Japan proposed an improved expression of Fujii and Takahashi’s formula using experimental data [6, 17]. Furthermore, Kuroda et al. [18] investigated the effect of bow shapes above the waterline for 6500 TEU containerships using a model test, and they proposed the application of a bluntness to determine the coefficients of their empirical formula, which is also known as the NMRI formula. A systematic comparison between the above formulae and different numerical methods for added resistance computation was conducted by Seo et al. [19].

Several studies were also performed based on a numerical method. Kihara et al. [20] adapted a nonlinear time-domain approach based on the high-speed strip theory to study the effect of the above-water bow form on the added resistance in waves. Orihara and Miyata [12] solved ship motions under regular head-wave conditions, and evaluated the added resistance of an SR-108 containership (typically known as an S175 containership) in waves using a CFD simulation method called WISDAM-X. They provided computational and experimental results with different bow shapes for the model containership, and confirmed that its sharp bow shape provides a smaller added resistance in waves. Orihara et al. [21] also applied WISDAM-X to predict the added resistance in head and oblique waves for different bow shapes, e.g., Ax-bow and Leadge-bow. Moreover, they compared the resistance for full load and ballast conditions. To investigate the physical mechanism of the reduction of added resistance in waves, flow features such as the time-averaged added pressure on the ship surface and the wave contour around the ship were examined.

In this study, a computational code [22] based on a Cartesian-grid method is applied to simulate the added resistance in short waves of the KVLCC2 hull with different bow shapes—the original KVLCC2, an Ax-bow type, and a Leadge-bow type—and different wave amplitudes. In the present numerical method, a first-order fractional step method was applied for velocity–pressure coupling, and the tangent of hyperbola for interface capturing (THINC) scheme [23] was used along with a weighted line interface calculation (WLIC) method [24] as a fluid interface capturing method. A solid body was embedded in a Cartesian grid, and a signed distance function was calculated in each computational grid to determine the volume fraction of the body inside a grid. Based on the convergence test of the time window and the number of grid points, the computed added resistance in waves was compared with experimental data. Further, the characteristics of the surge force for different wave amplitudes were examined by comparing the wave elevation around the bow. In addition, harmonic analyses of the time history of the surge force were conducted to compare the relative magnitude of higher harmonic components with respect to the magnitude of the first harmonic component. By investigating the instantaneous free-surface shapes and distribution of the added pressure on the ship surface, this study discusses the effects of the wave amplitude and bow shape on the added resistance in short waves. Finally, the time-averaged added pressure was obtained from the time history of the added pressure on each triangular surface mesh, which represents the ship surface, and the distribution characteristics on the ship surface were investigated for each bow shape and wave amplitude.

2 Numerical method

2.1 Flow solver

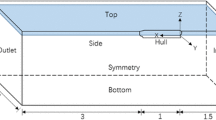
The present numerical code was developed by Yang et al. [22] and validated to determine the ship motion and the added resistance in waves. Because details of the present numerical method are described in that paper, here, we briefly explain the numerical procedure. The wave–ship interaction problem is considered as a multi-phase problem with water, air, and solid phases [25]. A solid body is embedded in a Cartesian grid, and to identify the different phases in each grid, the volume-fraction functions, ϕ m , are defined for the liquid (m = 1), gas (m = 2), and solid body (m = 3), as shown in Fig. 1. The origin of the right-handed coordinate system is located at the center of gravity of the ship moving with constant advancing speed, U. The x-axis points from the ship bow to the stern and the positive z-axis points upward in the direction normal to the mean water level. The y-axis is normal to the other two axes. The incident wave is approaching from the end of the negative x-axis with amplitude A and frequency ω.

Fig. 1
figure 1

Coordinate system and definition of volume-fraction functions

Full size image

The free surface is determined using an interface-capturing method, and the volume-fraction function for the liquid phase is calculated by solving the following advection equation:

$$\frac{{\partial \phi_{1} }}{\partial t} + \underline{u} \cdot \nabla \phi_{1} = 0.$$
(1)

To solve the advection equation, various numerical methods have been proposed in the literature. Of those methods, the tangent of hyperbola for interface capturing (THINC; Xiao et al. [23]) scheme with the weighed line interface calculation (WLIC; Yokoi [24]) method is used in the present computation. After calculating the volume-fraction function for the solid phase, which will be explained in the next section, the volume-fraction function of the air phase can be obtained from a simple constraint, i.e., the sum of the volume-fraction functions is equal to one in each grid.

In the fluid domain, the governing equations for an incompressible and inviscid fluid flow are the continuity and Euler equations, which are written in conservative forms as follows:

$$\int_{\varGamma } {\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right){\text{d}}S} = 0,$$
(2)
$$\frac{\partial }{\partial t}\int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} {\text{d}}V} + \int_{\varGamma } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right){\text{d}}S} = \frac{1}{\rho }\left[ { - \int_{\varGamma } {p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} {\text{d}}S} + \int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}_{b} {\text{d}}V} } \right],$$
(3)

where Ω indicates the control volume, and Γ represents the control surface enclosing the control volume. \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}\) is a unit outward normal vector on Γ. ρ is the fluid density, and p and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}\) denote the pressure and velocity vectors, respectively. In addition, \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}_{b}\) indicates the body-force vector.

The velocity and pressure are coupled using the fractional-step method, involving a solving procedure that is divided into three steps, one advection, and two non-advection phases as follows:

$$\frac{{\int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{*} {\text{d}}V} - \int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{n} {\text{d}}V} }}{\Delta t} + \int_{\varGamma } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{n} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{n} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right){\text{d}}S} = 0,$$
(4)
$$\frac{{\int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{**} {\text{d}}V} - \int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{*} {\text{d}}V} }}{\Delta t} = \frac{1}{{\rho^{n + 1} }}\int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}_{b} {\text{d}}V},$$
(5)
$$\frac{{\int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{n + 1} {\text{d}}V} - \int_{\varOmega } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{**} {\text{d}}V} }}{\Delta t} = - \frac{1}{{\rho^{n + 1} }}\int_{\varGamma } {p^{n + 1} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} {\text{d}}S}.$$
(6)

The superscripts (n, *, **, n + 1) indicate intermediate values during time advancement. The free-surface capturing method employed in this study is the semi-Lagrangian method, which cannot allow a Courant–Friedrichs–Lewy (CFL) number that is larger than unity, and which has first-order accuracy in time. Therefore, the first-order accurate fractional-step method is applied in this study. The pressure field is calculated by solving the pressure Poisson equation, which is obtained by taking the divergence of Eq. 6, and using the continuity equation and the divergence theorem.

$$\nabla \left( {\frac{1}{{\rho^{n + 1} }}\int_{\varGamma } {p^{n + 1} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} {\text{d}}S} } \right) = \frac{1}{\Delta t}\int_{\varGamma } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}^{**} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} {\text{d}}S}.$$
(7)

Spatial discretization is carried out based on the finite-volume approach with staggered variable allocation. The surface integration is approximated using a midpoint rule, and the cell center value is interpolated using a limiter function. For the limiter function, a monotonized central (MC) limiter [26] is used in this study. A directional splitting approach is applied to consider multidimensional effects. Other spatial discretization is conducted based on the second-order central-difference scheme.

Incident waves are generated from the end of the negative x-axis, and the boundary conditions for the velocity and the volume-fraction function of the liquid phase can be calculated from Stokes’ linear-wave solution. The domain-stretched method is adopted to apply the linearized solution above the mean water level, and the incident velocity is adjusted so that the net flux during one period is maintained as zero. To simulate more than 20 wave periods without reflected waves, a damping zone is located from the end of the positive x-axis. The damping zone size is set to twice the incident wavelength, λ for all subsequent computations. As shown in Fig. 2, the real profile of the incident wave is similar to the Stokes’ second-order solution even though the linear-wave solution was used for the wall boundary condition. Here, the wave steepness, kA, is 0.157 which is the largest wave-amplitude case in this study and the wave elevation was measured at 2λ away from the side wall.

Fig. 2
figure 2

Comparisons of wave elevations between numerical solution and Stokes wave solutions, kA = 0.1571

Full size image

2.2 Treatment of immersed solid body

As mentioned in the previous section, an arbitrary body was embedded in a Cartesian grid, and it was identified using a volume-fraction function of the solid body. To calculate the volume fraction of the solid body in each cell, a level-set-based method is applied. For each Cartesian-grid point, the signed distance from the ship surface which is represented by the triangular surface mesh is calculated using a simple transformation of a three-dimensional (3D) triangle into a two-dimensional (2D) unit right triangle. After obtaining the signed distance field from the triangular surface for each Cartesian-grid point, the volume-fraction function can be calculated using a smoothed Heaviside function.

$$\phi_{3} = H_{\alpha } \left( \psi \right) = \left\{\begin{array}{lll} 0 &\quad if\; \psi < - \alpha \\ \frac{1}{2}\left[ {1 + \frac{\psi }{\alpha } + \frac{1}{\pi }\sin \left( {\frac{\pi \psi }{\alpha }} \right)} \right] &\quad if \;\left| \psi \right| \le \alpha \\ 1 & \quad if \;\psi > \alpha \end{array}\right.$$
(8)

where ψ is a signed distance function, and α is a smoothing length, which is fixed as half of the diagonal distance of the smallest cell in this study. The detailed procedure and quantitative comparison of linear restoring coefficients and displacement can be found in Yang et al. [22].

To impose a body-boundary condition on the ship surface, a volume-weighted formulation is used.

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{u}} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} \left( {1 - \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} } \right) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U}_{\text{body}} \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} ,$$
(9)

where \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\hat{u}}\) is the corrected fluid velocity; \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U}_{\text{body}}\) is the body velocity; and \(\phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }}\) is the body-volume fraction in the corresponding velocity-control volume. In a similar way, the free-slip body-boundary condition on the ship surface can be derived as follows:

$$\hat{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} } = \left\{ {\begin{array}{ll} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} \quad } \\ {\left[ {\left( {1 - \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} } \right)\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right) + \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U}_{\text{body}} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right)} \right]\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} + \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} - \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right] = \left[ {\left( {1 - \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} } \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{N} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} + \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{N} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U}_{\text{body}} } \right] + \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{I} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{N} } \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} \quad } \\ {\left( {1 - \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} } \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} + \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U}_{\text{body}} \quad } \\ \end{array} } \right.{\kern 1pt} \begin{array}{ll} {if\;\,\,\phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} = 0.0} \\ {if\,\,\;0.0 < \phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} < 0.5} \\ {if\,\,\;\phi_{3}^{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} }} \ge 0.5} \\ \end{array} ,$$
(10)

where \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}\) is the surface normal and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{I} ,\,\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{N}\) indicate the identity tensor and normal dyad, respectively. Because the present numerical method identifies a ship in a Cartesian grid based on the volume-fraction function in each computational cell, the ship interface has finite thickness. The iso-surface of the volume-fraction function of the body, which is equal to 0.5, can be considered as the ship surface. Thus, the present numerical method has a limitation on wave-body interaction problems with very sharp geometry.

Figure 3 shows an example of the fluid velocity distribution in the still-water level section (z = 0) for the advancing KVLCC2 in calm water. In this case, the Froude number, Fn, is equal to 0.142. The velocity outside of the ship surface flows along the tangential direction to the ship surface, while the corrected fluid velocity inside the ship surface is almost the same as the body velocity.

Fig. 3
figure 3

Distribution of velocity vector around advancing ship bow: KVLCC2, Fn = 0.142

Full size image

The force and moment acting on the body are calculated as follows:

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{F} = - \iint_{{S_{B} }} {p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} {\text{d}}S} = - \sum\limits_{l = 1}^{{n{\text{Face}}}} {p_{l} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}_{l} \Delta S_{l} } ,$$
(11)
$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M} = - \iint_{{S_{B} }} {\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{cg} } \right) \times \left( {p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right){\text{d}}S} = - \sum\limits_{l = 1}^{{n{\text{Face}}}} {\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{l}^{c} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{cg} } \right) \times \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}_{l} p_{l} \Delta S_{l} }$$
(12)

where nFace denotes the number of triangular surfaces, and \(p_{l} ,\,\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n}_{l} ,\,\,{\text{and}}\,\Delta S_{l}\) denote the interpolated pressure, normal vector, and area of the lth triangular surface, respectively. \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{l}^{c}\) is the center coordinate of each triangular surface. The added resistance can be calculated by subtracting the calm-water resistance from the mean surge force in the presence of the incident wave. In both cases, the same mesh around the ship should be used to obtain a consistent added resistance, and it should be noted that there may be a difference in the calm-water resistance for the experiment and real ship because the viscosity was ignored in the present numerical method.

3 Results and discussion

3.1 Test condition

The added resistance in short waves is dominantly affected by the diffraction waves around the ship bow region. Thus, the bow shapes and wave amplitude of the incident wave significantly affect the added resistance in short waves. In the present study, three different bow shapes of KVLCC2—original KVLCC2, Ax-bow type and Leadge-bow type—are considered with different wave amplitudes. The idea of the Ax-bow and Leadge-bow was proposed by the Universal Shipbuilding Corporation [21]. Currently employed KVLCC2 bow shapes were designed by Daewoo Shipbuilding & Marine Engineering (DSME), and were provided by the Korea Research Institute of Ships and Ocean Engineering (KRISO) as a ministry project [27]. The main specifications of these ships are given in Table 1.

Table 1 Main specification of computational models
Full size table

The body plans of each bow shape are given in Fig. 4, and examples of the surface triangle mesh for the Ax-bow type and Leadge-bow type hulls are given in Fig. 5. The only difference between the original KVLCC2 and Ax-bow type is the bow shape above the still-water level, and other parts of the ship have the same geometry. The Ax-bow type has a sharp bow shape, which is extended along the x-direction 8 m from the fore perpendicular (F.P.). On the other hand, the Leadge-bow type has a relatively slender bow shape.

Fig. 4
figure 4

Body plans for KVLCC2 with different bow shapes [27]

Full size image
Fig. 5
figure 5

Examples of surface triangle mesh for Ax-bow type and Leadge-bow type

Full size image

As the wave amplitude increases, the nonlinearity of incident waves becomes important, and there may be breaking waves around the ship bow. To investigate the effect of the wave amplitude together with the bow shape on the added resistance at short wavelengths, in this paper, we consider four different wave amplitudes—kA = 0.0628, 0.0942, 0.1257, and 0.1571. The incident wavelength is fixed as half of the ship length, and the heave and pitch motions of the ship are free for both experiment and computation, while the other ship motions are restricted. For all computations, the Froude number is equal to 0.142 and only head waves are considered. The added resistance with respect to the wavelength using the present numerical method is presented in Yang et al. [22].

3.2 Convergence test

In short waves, the added resistance is usually sensitive to the resolution of the computational grid or panel [19]. Even though a grid system is sufficient to obtain converged solutions for the heave and pitch motion responses, the accurate prediction of the added resistance in waves requires a finer grid system. Thus, the grid-convergence test should be performed to obtain a reliable numerical result.

Grid conditions for grid-convergence testing of the original KVLCC2 are given in Table 2. The wave amplitude is kA = 0.0628 and the wavelength is half of the ship length. The number of mesh points is varied from around two million to five million. The added resistance values for each grid system are plotted in Fig. 6, and the converged behavior can be found after four million grid points—Grid3. Based on the results between Grid1 and Grid2, the grid size in the vertical (z-) direction significantly affects the added resistance. Furthermore, by comparing the results from Grid2, Grid3, and Grid4, the longitudinal (x-) direction grid size is also important, while the effect of spanwise (y-) direction grid spacing is relatively small in the present numerical method.

Table 2 Grid conditions for grid-convergence test
Full size table
Fig. 6
figure 6

Grid-convergence test of added resistance in short waves, original KVLCC2, kA = 0.0628, Fn = 0.142, λ/L = 0.5

Full size image

Figure 7 shows a comparison of the wave contour near the bow region for different grid systems. The wave contour represents the difference between wave elevations in the wave and in calm water, and it is normalized by the amplitude of the incident wave. In the present numerical method, the wave elevation is calculated by summing the volume-fraction function of water from the bottom to the top of the domain for each (x, y) coordinate. Thus, it should be noted that an incorrect wave elevation could be calculated near the bulbous bow or the breaking-wave region. Most wave patterns appear to be very similar to each other, but there is a difference near the ship surface of the bow region. Wave elevations along the ship surface differ slightly from each other, and the finest case shows slightly higher wave elevation than the other cases. This increases the added resistance because according to the potential theory, the water-line integration of the relative wave elevation is a dominant component of the added resistance in short waves.

Fig. 7
figure 7

Comparison of wave contour near the ship bow for different grid systems: original KVLCC2, kA = 0.0628, Fn = 0.142, λ/L = 0.5

Full size image

The sensitivity of the size of the time window for post-processing is also examined and the results are shown in Fig. 8 for different wave amplitudes. The added resistance in short waves shows converged behavior after more than seven periods from the time history of the surge force are used for post-processing. In the present paper, 10 periods from the time history are applied to calculate the mean value of the surge force and Grid4 is used for the subsequent computations.

Fig. 8
figure 8

Convergence test for size of time window: original KVLCC2, Fn = 0.142, λ/L = 0.5

Full size image

3.3 Computational results

In Fig. 9, the normalized added resistance in short waves is summarized for various wave amplitudes and bow shapes. Hollow symbols represent the experimental results obtained by Lee et al. [27] and the symbols with the solid circle, triangle, and rectangular shapes are the present computational results for original KVLCC2, Ax-bow type, and Leadge-bow type, respectively. In addition, the calculation results obtained by the Rankine panel method (RPM) [19] based on the weakly nonlinear formulation are represented using a filled circle symbol with a dash-dot-dot line for the original KVLCC2 only. As reported in the literature, the Ax-bow type provides a slightly smaller added resistance compared with that of the original KVLCC2, while the Leadge-bow type gives the smallest added resistance of the three bow shapes. The present numerical method shows a slightly overestimated added resistance in short waves for all wave amplitudes compared with the experimental results. From the results obtained experimentally and using the present numerical method, the added resistance in short waves, which is normalized by the square of the wave amplitude, decreases as wave amplitude increases. On the other hand, the Rankine panel method provides almost constant added resistance regardless of the wave amplitude, even though it is based on a weakly nonlinear formulation, in which nonlinear restoring and Froude–Krylov forces are additionally considered. Because the added resistance in short waves is mainly affected by diffraction waves, nonlinear forces due to diffraction waves should be considered to correctly predict the added resistance in short waves for different wave amplitudes.

Fig. 9
figure 9

Comparison of added resistance in short waves for different bow shapes: Fn = 0.142, λ/L = 0.5

Full size image

The reduction of added resistance for the Leadge-bow type compared with the original hull is summarized in Table 3. Because the Leadge-bow type hull is 2.5 % longer than the others, both non-dimensional and dimensional values are considered. The average differences of non-dimensional and dimensional values are 29.7 and 27.9 %, respectively. The Leadge-bow type hull provides about 30 % reduction of added resistance compared with the original hull. The average difference of dimensional value is slightly smaller than that of non-dimensional value.

Table 3 Reduction of Added Resistance for different bow shapes
Full size table

It should be noted that even in the experiment, a large variation in the added resistance is observed, especially for small wave amplitudes. Furthermore, as shown in the previous section, the present computational method is very sensitive to the grid size for predicting the added resistance. Thus, to determine the total resistance of a ship in a seaway, one should take care when applying the computational or experimental results of the added resistance in short waves.

To investigate the surge force characteristics, the wave elevation around the ship bow and the surge force are compared in Fig. 10, for the original KVLCC2 with kA = 0.0628 and 0.1571. The dashed lines represent the surge force and wave elevation for the small wave amplitude (kA = 0.0628) case, while the large amplitude (kA = 0.1571) case is shown by the solid line. The wave elevation is computed at (x/L, y/L) = (−0.5, 0.032), which is very close to the ship bow surface. The steady wave elevation is subtracted from the measured wave elevation in the presence of the incident wave, and the wave elevation is normalized by the amplitude of the incident wave. The surge force is normalized by the peak value of the surge force, F peak, for each wave-amplitude case. As mentioned in the previous section, the added resistance in short waves is mainly affected by the wave elevation along the ship surface. Thus, the surge force shows similar behavior when compared to the relative wave elevation around the ship bow. In both cases, the ratio |F trough|/F peak is less than 1.0, where F trough indicates the trough value of the surge force. For the case with a small amplitude (kA = 0.0628), the ratio is about 0.7, while the ratio is 0.6 for the case with a large amplitude (kA = 0.1571). The ratio |F trough|/F peak indicates the asymmetry of the surge force, and it therefore represents a degree of nonlinearity.

Fig. 10
figure 10

Comparison between surge force and wave elevation at (x/L, y/L) = (−0.5, 0.032): original KVLCC2, kA = 0.0628 and 0.1571, Fn = 0.142, λ/L = 0.5

Full size image

To examine more details of the nonlinearity of the surge force, the harmonic analyses of the surge force are conducted for both wave amplitudes. The surge force can be represented by the summation of the harmonic oscillation components as follows [28]:

$$F_{x} \left( t \right) = \text{Re} \left( {\sum\limits_{k}^{{}} {F_{k} e^{{ik\omega_{\text{e}} t}} } } \right),$$
(13)

where F k is the magnitude of the kth-harmonic component, i = \(\sqrt { - 1}\) is the complex unit, and ω e indicates the encounter wave frequency.

To compare the magnitude of each component for all wave amplitudes, the relative magnitude of each harmonic component with respect to the magnitude of first harmonic component is presented in Fig. 11. It was shown that the second-, third- and fourth-harmonic parts of the inline force on a circular cylinder become comparable to each other when the wave amplitude is close to the cylinder radius [29, 30]. As the wave amplitude increases, the relative magnitude of the higher components increases almost linearly, and the third-harmonic component increases rapidly for the case of the largest wave amplitude (kA = 0.1571). The magnitudes of the second- and third-harmonic components are more than 10 % of the fundamental component, while the magnitudes of the fourth- and fifth-harmonic components are about 5 and 2.5 %, respectively, when kA = 0.1571.

Fig. 11
figure 11

Comparison of relative magnitude of each harmonic component with respect to first-order component: original KVLCC2, Fn = 0.142, λ/L = 0.5

Full size image

The time histories of the surge force for different bow shapes and two wave amplitudes—kA = 0.0628 and 0.0942—are given in Fig. 12. The results for the calm-water case are also plotted with the results in waves. In the present computation, heave and pitch motions were set free and the viscosity was ignored. Thus, there is a small fluctuation in calm-water resistance. The magnitude of the surge force in waves is much larger than that in calm water. The normalized magnitude of the surge force decreases as the wave amplitude increases because the surge force is normalized by the square of the wave amplitude. All the bow shapes provide similar surge force time histories, and the magnitudes appear to be the same. However, the maximum surge forces have slightly different magnitudes depending on the bow shapes. The original KVLCC2 has the largest magnitude, and the Ax-bow type has a smaller magnitude than that of the original KVLCC2, while the Leadge-bow type has the smallest surge force of the three bow shapes.

Fig. 12
figure 12

Comparisons of surge force for KVLCC2 with different bow shapes, Fn = 0.142, λ/L = 0.5

Full size image

To investigate in more detail the wave patterns and pressure distribution around the ship bow, the time evolution of the free-surface shape and the added-pressure distribution are compared in Figs. 13, 14, 15 for different bow shapes and two wave amplitudes. The added pressure, Δp, is defined as follows:

Fig. 13
figure 13

Comparisons of free-surface shape for original KVLCC2, experiment (left) and computation (right), Fn = 0.142, λ/L = 0.5

Full size image
Fig. 14
figure 14

Comparisons of free-surface shape for Ax-bow type, experiment (left) and computation (right), Fn = 0.142, λ/L = 0.5

Full size image
Fig. 15
figure 15

Comparisons of free-surface shape for Leadge-bow type, experiment (left) and computation (right), Fn = 0.142, λ/L = 0.5

Full size image
$$\Delta p_{l} \left( t \right) = p_{l}^{{{\text{in}}\,{\text{wave}}}} \left( t \right) - p_{l}^{{{\text{in}}\,{\text{calm}}\,{\text{water}}}} ;\,\,l = 1,2, \cdots ,n{\text{Face,}}$$
(14)

where p inwave l and p incalmwater l indicate the pressure at the l-th triangular surface mesh of the advancing ship in waves and calm water, respectively. The added pressure is related to the added resistance because the direct pressure integration is used in the present method. In short wavelength, the ship motion can be neglected. Thus, we assumed that the surface normal vector of the ship is not a function of time. Also, the change of wetted surface can be considered in the density change in each Cartesian grid. Consequently, the density change affects the pressure value from the pressure Poisson equation. Thus, the pressure distribution is the only function of time which affects the added resistance in short waves using the present numerical method.

For the original KVLCC2, there was a breaking wave toward the front of the ship bow, while the breaking wave was generated at the side of the bow in the Ax-bow type. Because the original idea of the Ax-bow is that a diffraction wave is generated toward the side of the bow, there was also a breaking wave in that direction. Consequently, it reduces the added resistance in waves compared to the original KVLCC2. For the Leadge-bow type, a breaking wave occurred more towards the rear of the ship stem and the wave elevation was low compared with that of the other two bow shapes.

As the wave amplitude increases, an overturning type of breaking wave can be clearly observed, while the pattern of the added-pressure distribution is similar to that of the case with the smaller wave amplitude. For both the experimental and computational results, a similar breaking wave is observed, while the experiment shows a much thinner water sheet that is like a jet flow. Because of the low resolution, and ignoring the surface tension, the present computation does not enable the formation of such a thin water-sheet layer. However, overall breaking-wave shapes and the positions at which they occur are comparable with the corresponding results obtained in the experiment. The second figure in each snapshot corresponds to the instant in time at which the maximum surge force occurs, which is shown by “B” in the time history of the surge force (Fig. 12). The first and third figures in each snapshot correspond to the instants in time at which ± T e/4 from “B”, which are shown by “A” and “C” in Fig. 12, respectively. Here, T e is the encounter period. The maximum added pressure is distributed near the free surface, and the overall added-pressure distribution is similar, even when there are breaking waves around the ship bow.

The added resistance in waves is the difference between the time-averaged mean surge forces for the cases in calm water and the incident wave. Thus, the time average of the added pressure on the ship surface is a meaningful physical quantity that can be used to examine the characteristics of the added resistance in waves. The time-averaged added pressure \(\overline{\Delta p}\) is presented in Fig. 16 for different bow shapes and wave amplitudes. Because the added resistance can be obtained by multiplying the time-averaged added pressure by the area and longitudinal component of the normal vector of each triangular surface, the results are plotted from a viewpoint that is normal to the ship transverse section. As shown in the time evolution of the added-pressure distribution around the ship surface (Figs. 13, 14, 15), the dominant component of the time-averaged added pressure is distributed near the free surface. The maximum value of the time-averaged added pressure is observed along the mean position of the distribution, and the maximum magnitude is approximately half of the magnitude of the linear dynamic pressure, ρgA. The magnitude is attenuated along the vertical side and ship shoulder. The dominant distribution of the time-averaged added pressure corresponds to the integration of the relative wave elevation along the mean water line in the linear potential theory. Furthermore, a small amount of negative added pressure can be observed below the still-water level, and it corresponds to the quadratic terms in Bernoulli’s equation.

Fig. 16
figure 16

Comparisons of distribution of time-averaged added pressure on ship surface: kA = 0.0628, 0.0942, 0.1257, and 0.1571 (from left to right), Fn = 0.142, λ/L = 0.5

Full size image

The distribution shape of the time-averaged added pressure is almost identical regardless of the bow shape, while the thickness of the distribution shape becomes large as the incident wave amplitude increases. However, a different distribution was observed around the ship bow in the Ax-bow type. Because of the sharp edge of the Ax-bow type, the flow is divided into two parts and, consequently, the distribution of the time-averaged added pressure is disconnected around the edge of the ship bow. For the Leadge-bow type, which has a relatively slender shape, the overall magnitude of the time-averaged added pressure is slightly smaller than that of the other two bow shapes. This result confirms that the bluntness of the ship bow is also an important factor that affects the added resistance in short waves.

The mean position of the added-pressure distribution, η 0, is defined as the vertical position at which the maximum of the time-averaged added pressure occurs in each ship section along the longitudinal direction. In all cases, η 0 follows a certain wave profile instead of being located along the still-water level, z = 0. Figure 17 shows a comparison of η 0 for the original KVLCC2 with the profile of the steady-wave elevation, η steady along the ship surface, as measured by Kim et al. [31]. Both the numerical and experimental results show similar profiles, and it can be considered that the incident wave and diffraction wave oscillate about the steady-wave elevation profile as the mean position. Usually, the linearization of free-surface boundary conditions in potential theory is based on the still-water level. However, in some cases, such as the case when a ship has large variations in its bow shape in the vertical direction due to large flares, the linear potential theory provides an underestimated added resistance in short waves [19]. This can be improved by reformulating the linearization of the free-surface boundary conditions with respect to the steady-wave elevation [32, 33].

Fig. 17
figure 17

Comparison of the maximum position of time-averaged added pressure along the longitudinal ship section and the steady-wave elevation from an advancing KVLCC2 in calm water [31]: Fn = 0.142, λ/L = 0.5

Full size image

4 Conclusions

The added resistance in short waves for KVLCC2 hull with different bow shapes—original KVLCC2, Ax-bow type, and Leage-bow type—and various wave amplitudes were calculated using a Cartesian-grid method. Based on the results of present study, the following conclusions can be made:

  • The sensitivity of the time window for post-processing and grid spacing has been studied, and a converged solution can be obtained for both parameters. However, the grid sensitivity was somewhat high for the present numerical method, and care must be taken to determine the total resistance of a ship, including the added resistance in short waves.

  • Based on the harmonic analysis of the surge force, the second- and third-harmonic components become important as the amplitude of the incident wave increases. For the wave amplitudes considered in the present study, the relative magnitude of both second- and third-harmonic components exceeds 10 % of the magnitude of the fundamental component.

  • The distribution of the time-averaged added pressure on the ship surface has a similar pattern, even when waves are breaking around the ship bow. Furthermore, the distribution range in the vertical direction increases as the wave amplitudes increase, and the local value of the added pressure changes according to the slenderness and sharpness of the ship bow.

  • The maximum position of the time-averaged added pressure in each section along the longitudinal direction of the ship follows a profile that is similar to that of the steady-wave elevation from the advancing ship in calm water.