Abstract
In this paper, a mathematical model is developed for the maneuvering motion of a naval ship and bifurcations of its equilibrium are identified in roll-coupled motion. The subject ship is a high-speed surface combatant with twin-propeller twin-rudder system. Captive model tests are conducted for the ship using planar motion mechanism. Maneuvering coefficients are calculated by polynomial curve fitting of the test data. Uncertainty distribution in the coefficients is assumed same as that of the curve fitting errors. Uncertainty in the model coefficients is propagated to full-scale simulation results by the stochastic response surface method (SRSM). This method is computationally efficient as compared to standard Monte Carlo simulation technique. The SRSM uses polynomial chaos expansion of orthogonal to fit any probability distribution. Bifurcation analysis of the mathematical model is performed by varying the vertical center of gravity as the bifurcation parameter. Hopf bifurcation is identified. It is found that the bifurcations occur due to the coupling of roll motion with sway, yaw motion and rudder angle. In the presence of wind, roll angle response in bifurcation diagram is discussed.


























Similar content being viewed by others
Abbreviations
- \( a_{0} ,a_{1} ,a_{2} \) :
-
Coefficients representing \( K_{\text{T}} \)
- \( a,b \) :
-
Proportional and derivative control parameters, respectively, of autopilot equation
- \( a_{\text{H}} \) :
-
Ratio of additional lateral force induced on ship hull by rudder action to the rudder force
- \( A_{\text{R}} \) :
-
Lateral area of a rudder (=span × chord)
- \( C^{\prime}_{{{\text{R}}\delta }} ,C^{\prime}_{{{\text{R}}r}} \) :
-
Rudder flow straightening coefficients for rudder angle and yaw rate, respectively
- \( C_{\text{R}} ,h_{\text{R}} \) :
-
Rudder chord and span, respectively
- \( D_{\text{P}} \) :
-
Propeller diameter
- \( f_{\alpha } \) :
-
Rudder normal force coefficient
- Fn:
-
Froude number
- \( F_{\text{RX}} \), \( F_{\text{RY}} \) :
-
Surge and sway forces acting on rudder stock, in rudder-fixed coordinate system
- \( g \) :
-
Acceleration due to gravity
- \( I_{x} \), \( I_{z} \) :
-
Moment of inertia of the ship about \( x \) and \( z \) axis, respectively
- \( I_{\text{P}} \) :
-
Moment of inertia of the propeller and shaft
- \( J_{x} \), \( J_{z} \) :
-
Added mass moment of inertia of ship with respect to \( x \) and \( z \) axis, respectively
- \( K_{{\dot{v}}} \), \( K_{{\dot{r}}} \), \( N_{{\dot{v}}} \) and \( N_{{\dot{r}}} \) :
-
Added mass moment of inertia
- \( K_{\text{T}} \), \( K_{\text{Q}} \) :
-
Thrust and torque coefficient, respectively
- \( L_{\text{OA}} \) :
-
Overall ship length
- \( L_{\text{PP}} \) :
-
Ship length between perpendiculars
- \( l_{1} \) :
-
First Lyapunov coefficient
- \( m \) :
-
Mass of the ship
- \( m_{x} = - X_{{\dot{u}}} \) :
-
Added mass in \( x \) direction of the ship
- \( m_{y} = - Y_{{\dot{v}}} \) :
-
Added mass in \( y \) direction of the ship
- \( n_{0} \) :
-
Initial engine speed
- \( n_{\text{P}} \) :
-
Propeller revolutions
- \( n_{\text{PMM}} \) :
-
Revolution of PMM
- \( P_{\text{E}} \) :
-
Engine power
- \( Q_{0} \) :
-
Initial engine torque
- \( q_{0} ,q_{1} ,q_{2} \) :
-
Coefficients representing \( K_{\text{Q}} \)
- \( Q_{\text{E}} ,Q_{\text{P}} ,Q_{\text{R}} \) :
-
Engine, propeller, and rudder torque (acting on rudder stock), respectively
- \( {\text{Ry}} \) :
-
Rudder lift
- \( T \) :
-
Ship draft
- \( {\text{TD}} \) :
-
Turning diameter
- \( T_{\text{E}} \) :
-
Time constant of steering gear
- \( t_{{{\text{P}}0}} ,t_{\text{P}} \) :
-
Thrust deduction factor in straight moving and maneuvering motion, respectively
- \( T_{\text{P}} \) :
-
Propeller thrust
- \( T_{\text{PMM}} \) :
-
Time period of PMM
- \( t_{\text{R}} \) :
-
Rudder resistance deduction factor
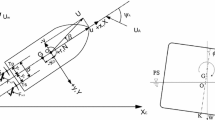
- \( u,v,p,r \) :
-
Surge, sway, roll, and yaw velocity at midship, respectively
- \( U_{\text{C}} \) :
-
Towing carriage speed
- \( U_{\text{R}} \) :
-
Inflow velocity to rudder
- \( U_{X} ,U_{Y} ,U_{N} \) :
-
Uncertainty in measured surge, sway force and yaw moment
- \( w_{{{\text{P}}0}} ,w_{\text{P}} \) :
-
Wake coefficient at propeller location in straight moving and maneuvering motion, respectively
- \( w_{\text{R}} \) :
-
Wake coefficient at rudder location in maneuvering motion
- \( (x_{\text{G}} ,y_{\text{G}} ,z_{\text{G}} ) \) :
-
Position of center of gravity of ship from the origin \( O \)
- \( x_{\text{H}} \) :
-
Rudder-hull interaction coefficients
- \( x_{\text{P}} ,x_{\text{R}} \) :
-
Longitudinal position of propeller and rudder, respectively
- \( X,Y,N,K \) :
-
Total surge force, sway force, yaw moment, and roll moment at the midship, respectively
- \( X_{\text{H}} ,Y_{\text{H}} ,N_{\text{H}} ,K_{\text{H}} \) :
-
Surge force, sway force, yaw moment, and roll moment due to the bare hull at the midship, respectively
- \( X_{\text{P}} ,N_{\text{P}} \) :
-
Surge force and yaw moment due to the twin-propeller at the midship, respectively
- \( X_{\text{R}} ,Y_{\text{R}} ,N_{\text{R}} ,K_{\text{R}} \) :
-
Surge force, sway force, yaw moment, and roll moment due to the twin-rudder at the midship, respectively
- \( X_{\text{W}} ,Y_{\text{W}} ,N_{\text{W}} ,K_{\text{W}} \) :
-
Surge force, sway force, yaw moment, and roll moment due to wind at the midship, respectively
- \( y_{\text{P}} ,y_{\text{R}} \) :
-
Lateral position of propeller and rudder, respectively
- \( Z_{\text{R}} \) :
-
Vertical center of rudder force
- \( \alpha_{\text{R}} \) :
-
Effective rudder inflow angle or effective angle of attack of rudder to flow
- \( \beta \) :
-
Ship drift angle
- \( \beta_{\text{P}} \) :
-
Geometrical drift angle induced at the propeller position due to ship motions
- \( \beta_{\text{R}} \) :
-
Geometrical drift angle induced at the rudder position due to ship motions
- \( \gamma_{\text{R}} \) :
-
Rudder flow straightening coefficient for drift angle
- \( \delta \) :
-
Rudder angle
- \( \delta_{0} \) :
-
Neutral rudder angle for straight motion
- \( \varepsilon \) :
-
Ratio of effective wake fraction in way of propeller and rudder
- \( \kappa \) :
-
Propeller race amplification factor
- \( \eta_{\text{S}} \) :
-
Shaft efficiency
- \( \eta_{\text{R}} \) :
-
Relative rotative efficiency
- \( \rho \) :
-
Water density
- \( \rho_{\text{A}} \) :
-
Air density
- \( \psi \) :
-
Heading angle of ship
- \( \psi_{\text{W}} \) :
-
Heading angle of wind
- \( \psi_{\text{R}} \) :
-
Relative heading angle between wind and ship
- \( \psi_{\text{A}} \) :
-
Absolute heading angle of ship in wind
- \( \phi \) :
-
Roll angle of ship
- \( \dot{\phi } \) :
-
The time derivative of a variable is denoted by a dot above the variable, e.g., \( \dot{\phi } \) is the time derivative of \( \phi \)
- \( {\prime } \) :
-
Non-dimensional value
- {S}:
-
Starboard
- {P}:
-
Portside
References
Strøm-Tejsen J, Chislett MS (1966) A model testing technique and method of analysis for the prediction of steering and manoeuvring qualities of surface vessels. Report no. Hy-7, Danish Technical Press
Son KH, Nomoto K (1981) On the coupled motion of steering and rolling of a high-speed container ship. J Soc Naval Arch Jpn 150:73–83
Eda H (1980) Maneuvering performance of high-speed ships with effect of roll motion. Ocean Eng 7(3):379–397
Lee SK, Fujino M (2003) Assessment of a mathematical model for the manoeuvring motion of a twin-propeller twin-rudder ship. Int Shipbuild Prog 50(1–2):109–123
Khanfir S, Hasegawa K, Nagarajan V, Shouji K, Lee SK (2011) Manoeuvring characteristics of twin-rudder systems: rudder-hull interaction effect on the manoeuvrability of twin-rudder ships. J Mar Sci Technol 16(4):472–490
Dash AK, Nagarajan V (2014) A stochastic response surface approach for uncertainty propagation in ship maneuvering. Int Shipbuild Prog 61:129–161. doi:10.3233/ISP-140110
Coraddu A, Dubbioso G, Mauro S, Viviani M (2012) Experimental investigation of asymmetrical propeller behavior of twin screw ships during maneuvers. In: Proceedings of international conference on marine simulation and ship maneuverability MARSIM 2012, Singapore
Schulten PJM (2005). The interaction between diesel engines, ship and propellers during manoeuvring. Ph.D. thesis, Delft University of Technology
AIAA Standard (1999) Assessment of experimental uncertainty with application to wind tunnel testing. AIAA S-071A-1999, Washington, DC
Coleman HW, Steele GW (1995) Engineering application of experimental uncertainty analysis. AIAA J 33(10):1888–1896
ITTC (1999) Uncertainty analysis in EFD, uncertainty analysis methodology 4.9-03-01-01. In: Proceedings, 22nd international towing tank conference, Seoul, Korea/Beijing, China
Simonsen CD (2004) PMM model test with DDG51 including uncertainty analysis. FORCE Technology, Denmark
Yoon H (2009) Phase-averaged stereo-PIV flow field and force/moment/motion measurements for surface combatant in PMM maneuvers. Ph.D. thesis, The University of Iowa
Benedetti L, Bouscasse B, Broglia R, Fabbri L, Gala FL, Lugni C (2004) PMM model test with DDG51 including uncertainty analysis. INSEAN, Italy
Mavris DN, Bandte O (1997). Comparison of two probabilistic techniques for the assessment of economic uncertainty. In: 19th annual conference of the international society of parametric analysts, New Orleans, LA, May 1997
Isukapalli SS (1999) Uncertainty analysis of transport-transformation models. Doctoral dissertation, Rutgers, The State University of New Jersey
Li D, Chen Y, Lu W, Zhou C (2011) Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables. Comput Geotech 38(1):58–68
Wiener N (1938) The homogeneous chaos. Am J Math 60(4):897–936
Ghanem RG, Spanos PD (1991) Stochastic finite elements: a spectral approach. Springer, New York
Bulian G, Nicolosi RG, Francescutto A. (2006) On the effect of uncertainty modeling in the hydrodynamic derivatives of a ship manoeuvring mathematical model. In: Proceedings of the seventh international conference on hydrodynamics ICHD (Oct, 2006). University of Naples ‘‘Federico II’’, Ischia, pp 359–368
Hirano M, Takashina J (2010) Ship maneuverability—theory and its application. Chapter 11: roll-coupling effects on ship maneuverability. Mitsui Akishima Research Laboratory, Japan
Yasukawa H, Yoshimura Y (2014) Roll-coupling effect on ship maneuverability. Ship Technol Res 61(1):16–32
Spyrou K (1995) Yaw stability of ships in steady wind. Ship Technol Res/Schiffstechnik 42(1):21–30
Falzarano J, Steindl A, Troesch A, Troger H (1991) Rolling motion of ships treated as bifurcation problem, vol 97. In: Bifurcation and Chaos: Analysis, Algorithms, Applications, International Series of Numerical Mathematics. Birkhäuser, Basel, pp 117–122
Francescutto A, Contento G (1999) Bifurcations in ship rolling: experimental results and parameter identification technique. Ocean Eng 26(11):1095–1123
Umeda N, Hashimoto H, Minegaki S, Matsuda A (2008) An investigation of different methods for the prevention of parametric rolling. J Mar Sci Technol 13(1):16–23
Virgin LN (1987) The nonlinear rolling response of a vessel including chaotic motions leading to capsize in regular seas. Appl Ocean Res 9(2):89–95
Dash AK, Nagarajan V, Sha OP (2015) Bifurcation analysis of high speed twin-propeller twin-rudder ship maneuvering model in roll-coupling motion. Nonlinear Dyn. doi:10.1007/s11071-015-2463-9
Dhooge A et al (2008) New features of the software MatCont for bifurcation analysis of dynamical systems. Math Comput Model Dyn Syst 14(2):147–175
Ogawa A, Kasai H (1978) On the mathematical method of manoeuvring motion of ships. Int Shipbuild Prog 25(292):306–319
Inoue S, Hirano M, Kijima K, Takashina J (1981) A practical calculation method of ship maneuvering motion. Int Shipbuild Prog 28(325):207–222
Yasukawa H, Yoshimura Y (2015) Introduction of MMG standard method for ship maneuvering predictions. J Mar Sci Technol 20(1):37–52
Rubis CJ (1972) Acceleration and steady-state propulsion dynamics of a gas turbine ship with controllable-pitch propeller. Trans SNAME 8:329–360
Naval Science & Technological Laboratory (NSTL), available in http://www.drdo.gov.in/drdo/labs/NSTL/English/index.jsp?pg=facility.jsp. Accessed 13 Mar 2016
Motora S (1960) On the measurement of added mass and added moment of inertia for ship motions: part 2. Added mass for the longitudinal motions. J Soc Naval Arch Jpn 106:59–62 (in Japanese)
Kuznetsov YA (2004) Elements of Applied Bifurcation Theory, vol 112. Springer, New York
Larger L, Goedgebuer JP, Erneux T (2004) Subcritical Hopf bifurcation in dynamical systems described by a scalar nonlinear delay differential equation. Phys Rev E 69(3):036210
Det Norske Veritas (1999) Rules for High Speed, Light Craft and Naval Surface Craft, Part 1, Chap 2, Section 2, p 8
National Transportation Safety Board (2001) USA: Aircraft Accident Report, NTSB/AAR-04/04, p 21
Dash AK, Nagarajan V, Sha OP (2015) Uncertainty assessment for ship maneuvering mathematical model. Int Shipbuild Prog 62:57–111. doi:10.3233/ISP-150117
Oltmann P (1996) On the influence of speed on the manoeuvring behaviour of a container carrier. In: Chislett MS (ed) Marine simulation and ship manoeuvrability. A. A. Balkema, Rotterdam, pp 515–523
Fujiwara T, Ueno M, Nimura T (1998) Estimation of wind forces and moments acting on ships. J Soc Naval Arch Jpn 183:77–90
Nagarajan V, Kang DH, Hasegawa K, Nabeshima K (2008) Comparison of the mariner Schilling rudder and the mariner rudder for VLCCs in strong winds. J Mar Sci Technol 13(1):24–39
Maritime Dynamics Laboratory, available in http://www.sspa.se/facilities/maritime-dynamics-laboratory. Accessed 13 Mar 2016
Kim YG, Kim SY, Kim HT, Lee SW, Yu BS (2007) Prediction of the maneuverability of a large container ship with twin propellers and twin rudders. J Mar Sci Technol 12(3):130–138
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Maneuvering model for hull forces and moments
The hull forces and moments are expressed at the midship. The mathematical expression for \( X_{\text{H}} \) is shown in Eq. 6.
where \( X_{*} \) represents the resistance of the ship.
The mathematical expression for \( Y_{\text{H}} \) and \( N_{\text{H}} \) is shown in Eq. 7.
The mathematical expression for \( K_{\text{H}} \) is shown in Eq. 8.
where \( K_{p} \) is the roll damping coefficient, \( mg\overline{GZ} \) is the roll restoring moment, \( z_{\text{H}} \) is the \( z \) coordinate of the point where the \( Y_{\text{H}} \) acts. \( KN \) depends on the geometric characteristics of the hull. It is computed for different heel angles at the constant displacement condition. The vessel is free to sink and trim. Once the \( KN \) is determined, the righting arm \( \overline{GZ} \) can be computed for any vertical center of gravity \( VCG \) corresponding to that displacement condition using the formula \( \overline{GZ} = KN - VCG\sin \phi \).
The mathematical expressions for \( X_{\text{P}} \), \( N_{\text{P}} \) and \( Q_{\text{P}} \) are shown in Eqs. 9 and 10.
The mathematical expression for forces (\( X_{\text{R}} \) and \( Y_{\text{R}} \)) and moment (\( N_{\text{R}} \) and \( K_{\text{R}} \)) induced at midship due to rudder are shown in Eq. 11.
where, \( s \): sin, \( c \): cos
The forces \( F_{\text{RX}} \), \( F_{\text{RY}} \) and torque \( Q_{\text{R}} \) are expressed as shown in Eq. 12.
The \( U_{\text{R}} \) and \( \alpha_{\text{R}} \) are expressed as shown in Eq. 13.
The longitudinal component of rudder inflow velocity \( u_{\text{R}} \) is expressed as shown in Eq. 14.
The lateral component of rudder inflow velocity \( v_{\text{R}} \) is expressed as shown in Eq. 15.
The wind forces and moment acting on the ship are estimated as shown in Eqs. 16 and 17.
To convert effective wind angle from our coordinate system to Fujiwara’s coordinate system we use Eq. 18.
where, \( C_{\text{X}} (\psi_{\text{A}} ) \), \( C_{\text{Y}} (\psi_{\text{A}} ) \), \( C_{\text{N}} (\psi_{\text{A}} ) \), \( C_{\text{K}} (\psi_{\text{A}} ) \) are the wind force coefficients. These coefficients are calculated for the present ship as per Fujiwara et al. [42] and Nagarajan et al. [43] and are shown in Fig. 27.
1.2 PMM experiment analysis
In the Strøm–Tejsen PMM experiment set up [1], the aft and forward part of the model is connected to two rotating discs through connecting rods and yoke. The PMM experiment analysis procedure for this set up is well known. Recently, some of the marine dynamics laboratories have carriage capable of generating X, Y and rotation motion using computer controlled carriage motion. In this type of facility, circular motion test, rotating arm test and PMM test can be done with the same set up. The layout of this type of PMM set up is shown in Fig. 28 [34]. The 1:19.2 scale model is tested in this type of set up. The kinematics of the set up permits static drift, pure sway, pure yaw and yaw + sway motions to be induced on the model. In Strøm–Tejsen’s set up, it was static drift, pure sway, pure yaw and drift + sway motions. The extraction of coefficients from this type of set up is described below. The model dynamics for pure sway and yaw motion is shown in Eq. 19.
where \( y \) is the lateral displacement and \( \psi \) is the angular displacement of the model ship.
The model dynamics for sway + yaw motion are shown in Eq. 20.
where \( s \): sin and \( c \): cos
The mathematical expressions for \( X_{\text{H}} \), \( Y_{\text{H}} \), \( N_{\text{H}} \) and \( K_{\text{H}} \) during pure sway motion are obtained by substituting \( r \) = 0, \( \dot{r} \) = 0, \( \phi \) = 0, \( p \) = 0 and \( \dot{p} \) = 0 in Eqs. 6–8, respectively. The mathematical expressions for \( X_{\text{H}} \), \( Y_{\text{H}} \), \( N_{\text{H}} \) and \( K_{\text{H}} \) during pure yaw motion are obtained by substituting \( v \) = 0, \( \dot{v} \) = 0, \( \phi \) = 0, \( p \) = 0 and \( \dot{p} \) = 0 in Eqs. 6–8, respectively. The mathematical expressions for \( X_{\text{H}} \), \( Y_{\text{H}} \), \( N_{\text{H}} \) and \( K_{\text{H}} \) during heel + yaw motion are obtained by substituting \( v \) = 0, \( \dot{v} \) = 0, \( p \) = 0 and \( \dot{p} \) = 0 in Eqs. 6–8, respectively. The mathematical expressions for \( X_{\text{H}} \), \( Y_{\text{H}} \), \( N_{\text{H}} \) and \( K_{\text{H}} \) during sway + yaw motion are obtained by substituting \( r \) = 0, \( \dot{r} \) = 0, \( p \) = 0 and \( \dot{p} \) = 0 in Eqs. 6–8, respectively.
Maneuvering coefficients during static tests are calculated by the least-square fit method. For this, the number of test cases should be more than twice of the number of coefficients present in the mathematical model. In dynamic tests, the mathematical model is expressed in harmonic form by substituting the PMM motions and the coefficients are calculated by Fourier series analysis. This is explained for pure sway motion in Eqs. 21 and 22.
where, \( s \): sin and \( c \): cos
where the variable \( F \) corresponds to \( Y \) or \( N \) or \( K \).
where, \( s \): sin, \( c \): cos
The explanation for sway + yaw motion is given in Eqs. 23 and 24.
where \( c \): cos, the variable \( F \) corresponds to \( Y \) or \( N \) or \( K \).
1.3 Development of the roll moment model
During bare and appended hull PMM tests with 1:19.2 scale geosym model, roll moment was not measured. Additional PMM tests are carried out at Fn = 0.24 for 1: 30 scale geosym model for measuring roll moment. For 1:30 scale geosym model, the PMM tests are conducted only for appended hull condition. The PMM test 1:30 scale model is tested in the Maritime Dynamics Laboratory (MDL) of SSPA, Sweden [44]. We analyzed the experiment data for determining the roll related coefficients. The tests cover static drift, static heel, static rudder, pure sway and pure yaw. The summary of tests conducted is shown in Table 7. The forces (surge and sway) and moments (yaw and roll) are recorded during the tests. The forces and torque acting on starboard rudder and total thrust for the propeller are recorded. In addition, roll decay and free running model tests are conducted. These test data are used to develop the roll moment model. The coefficients present in roll moment model have been described in the “Maneuvering model for hull forces and moments” in Appendix. The value of \( z^{\prime}_{\text{H}} \) and \( z^{\prime}_{\text{R}} \) are obtained from the static drift and static rudder test, respectively [45]. These are calculated by comparing the measured sway force and roll moment as shown in Fig. 29. A linear relationship is seen in both cases. The coefficients \( K^{\prime}_{{\dot{v}}} \) and \( K^{\prime}_{{\dot{r}}} \) are calculated by Fourier series analysis of pure sway and pure yaw test data, respectively. The coefficients \( K^{\prime}_{{\dot{p}}} \), \( K^{\prime}_{p} \), \( K^{\prime}_{ppp} \) are calculated from roll decay test. The coefficients \( K^{\prime}_{\phi } \) and \( K^{\prime}_{\phi \phi \phi } \) are from static heel test data as shown in Fig. 30. The drift + heel test were not conducted in SSPA [44]. Although drift + heel test were carried out at NSTL [34], the roll moment could not be measured. Therefore, the exact relation between measured sway force and roll moment is not known. Therefore, the non-dimensional roll moment due to \( v - \phi \) and \( r - \phi \) coupling motion is assumed to be about \( -z^{\prime}_{\text{H}} \) times of the nondimensional sway force, this makes the coefficients \( K^{\prime}_{vv\phi } \), \( K^{\prime}_{v\phi \phi } \), \( K^{\prime}_{rr\phi } \), and \( K^{\prime}_{r\phi \phi } \) as \( - z^{\prime}_{\text{H}} \) times of the \( Y^{\prime}_{vv\phi } \), \( Y^{\prime}_{v\phi \phi } \), \( Y^{\prime}_{rr\phi } \), and \( Y^{\prime}_{r\phi \phi } \), respectively.
1.4 Sensitivity analysis
A sensitivity analysis for the propeller revolution, propeller thrust, engine torque and rudder normal force in zigzag and turning simulations is carried out. In addition, sensitivity analysis for the overshoot angle and advance for zigzag and turning simulations, respectively, is also carried out. The sensitivity is calculated using Eq. 25.
where \( \theta_{yx} \) is the sensitivity of output \( y \) to input \( x \), \( \Delta a \) the perturbed value of each input, \( N_{t} \) is the total number of samples in time series. In Eq. 25, the model coefficients are individually multiplied by a factor of 1.1 (\( \Delta a = 0.10 \)) and the change in respective output is recorded as a percentage of the original value. This equation is valid for a constant time step simulation. For steady state analysis, turning maneuver is considered. The total simulation time is taken as 300 s. Only the steady state part (after 100 s of simulation start) is considered in sensitivity analysis. For transient analysis, the zigzag maneuver is considered. Three complete cycles of \( \delta \) change command is given. The root mean square (rms) of various parameters is taken for the entire time duration. All coefficients are sorted in decreasing order of their sensitivity value (positive or negative) for each output, sorting is performed exclusively for starboard propeller and rudder outputs. The first 15 sensitive coefficients shown in Fig. 31 are considered for uncertainty propagation [6]. Coefficient \( Y^{\prime}_{{\dot{v}}} \) and \( C^{\prime}_{Rr} \) have the largest impact on the prediction of engine torque during zigzag and turning maneuvers. Besides the hull model coefficients, the hull, propeller, and rudder interaction coefficients are also significantly sensitive. The influence of the coefficients present in windward rudder model is more as compared to that of leeward. In addition, it is higher in turning as compared to zigzag maneuver.
About this article
Cite this article
Dash, A.K., Chandran, P.P., Khan, M.K. et al. Roll-induced bifurcation in ship maneuvering under model uncertainty. J Mar Sci Technol 21, 689–708 (2016). https://doi.org/10.1007/s00773-016-0382-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00773-016-0382-1