Tracking control of underwater vehicle subject to uncertainties using fuzzy inverse desired trajectory compensation technique

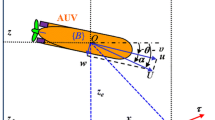
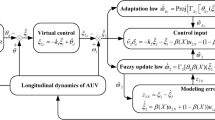
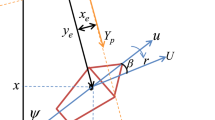
Abstract

Computed-torque controller plus fuzzy inverse desired trajectory compensation technique based on robust adaptive fuzzy observer is proposed to control underwater vehicle subject to uncertainties. A fuzzy inverse desired trajectory compensator is developed as a nonlinear filter at input trajectory level outside the control loop to address the issue of unavailable normalizing factor. A robust adaptive state observer with loose constraint on the position of the uncertainty function is proposed to evaluate the unavailable states. Numerical simulation results of regulation performance demonstrate that the observer solves the problem of strict constraint conditions on position uncertainties. Comparisons of tracking performance between the proposed control method and computed-torque controller are performed. The results confirm that compensation at the input trajectory offers better position tracking performance and easier practical implementation than other fuzzy compensation techniques at joint torque level. The proposed control approach is simulated and its efficiency is validated through the simulation of an underwater vehicle.

Appendices

Appendix 1: Dynamic modeling of underwater vehicle

The inertia matrix $M$ is divided into the rigid-body inertia $M_{\text{RB}}$ and the hydrodynamic added inertia $M_{\text{A}}$. The rigid-body inertial matrix, $M_{\text{RB}}$, expresses the inertial terms of the vehicle. As the underwater vehicle moves in water, an added inertia $M_{\text{A}}$ is used to represent the effective mass of the surrounding fluid as the vehicle accelerates. Rigid-body and added inertia matrix can be defined as follows:

$$M = M_{\text{RB}} { + }M_{\text{A}} = \left[ {\begin{array}{*{20}c} {mI_{3 \times 3} } & { - mS\left( {r_{g}^{b} } \right)} \\ {mS\left( {r_{g}^{b} } \right)} & {I_{0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } \\ {A_{21} } & {A_{22} } \\ \end{array} } \right]$$

(47)

where $m$ denotes the mass of the underwater vehicle; $I_{3 \times 3}$ is an identity matrix; $I_{0}$ is the inertia matrix of the vehicle; $r_{g}^{b} = \left[ {x_{g} ,y_{g} ,z_{g} } \right]^{T}$ is the vector from the coordinate origin of the inertial frame to center of gravity; $S\left( \lambda \right)$ is a skew-symmetric matrix, and $A_{11} = - \left[ {\begin{array}{*{20}c} {X_{{\dot{u}}} } & 0 & 0 \\ 0 & {Y_{{\dot{v}}} } & 0 \\ 0 & 0 & {Z_{{\dot{w}}} } \\ \end{array} } \right]$, $A_{12} = - \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & {Y_{{\dot{r}}} } \\ 0 & {Z_{{\dot{q}}} } & 0 \\ \end{array} } \right]$, $A_{21} = - \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & {M_{{\dot{w}}} } \\ 0 & {N_{{\dot{v}}} } & 0 \\ \end{array} } \right]$, $A_{22} = - \left[ {\begin{array}{*{20}c} {K_{{\dot{p}}} } & 0 & 0 \\ 0 & {M_{{\dot{q}}} } & 0 \\ 0 & 0 & {N_{{\dot{r}}} } \\ \end{array} } \right]$.

The Coriolis and centripetal matrix, $C\left( \upsilon \right)$, is divided into rigid-body term $C_{RB} \left( \upsilon \right)$ and hydrodynamic Coriolis and centripetal term $C_{A} \left( \upsilon \right)$. $C_{RB} \left( \upsilon \right)$ consists of the centripetal and Coriolis vectors of the vehicle, and $C_{A} \left( \upsilon \right)$ represents the hydrodynamic centripetal and Coriolis vectors originating from the surrounding fluid. The Coriolis and centripetal matrix is represented as follows:

$$\begin{aligned} C\left( \upsilon \right){\text{ = C}}_{RB} \left( \upsilon \right){\text{ + C}}_{A} \left( \upsilon \right) = \left[ {\begin{array}{*{20}c} {0_{3 \times 3} } & { - mS\left( {\upsilon_{1} } \right) - mS\left( {\upsilon_{2} } \right)S\left( {r_{g}^{b} } \right)} \\ { - mS\left( {\upsilon_{1} } \right) - mS\left( {\upsilon_{2} } \right)S\left( {r_{g}^{b} } \right)} & { - S\left( {I_{0} \upsilon_{2} } \right)} \\ \end{array} } \right] \hfill \\ \left[ {\begin{array}{*{20}c} {0_{3 \times 3} } & { - mS\left( {A_{11} \upsilon_{1} + A_{12} \upsilon_{2} } \right)} \\ { - mS\left( {A_{11} \upsilon_{1} + A_{12} \upsilon_{2} } \right)} & { - mS\left( {A_{21} \upsilon_{1} + A_{22} \upsilon_{2} } \right)} \\ \end{array} } \right] \hfill \\ \end{aligned}$$

When it can be roughly approximated and assumed that the vehicle has three planes of symmetry and the terms higher than second order are negligible, a diagonal structure of $D\left( \upsilon \right)$ with only linear and quadratic damping terms can be written as follows [2]:

$$\begin{aligned} D\left( \upsilon \right) = D{ + }D_{n} \left( \upsilon \right){ = - }diag\left\{ {X_{u} ,Y_{v} ,Z_{w} ,K_{p} ,M_{q} ,N_{r} } \right\}{ - } \hfill \\ diag\left\{ {X_{u\left| u \right|} \left| u \right|,Y_{v\left| v \right|} \left| v \right|,Z_{w\left| w \right|} \left| w \right|,K_{p\left| p \right|} \left| p \right|,M_{q\left| q \right|} \left| q \right|,N_{r\left| r \right|} \left| r \right|} \right\} \hfill \\ \end{aligned}$$

(48)

where $diag\left\{ {X_{u} ,Y_{v} ,Z_{w} ,K_{p} ,M_{q} ,N_{r} } \right\}$ is linear coefficient which can be derived by hydrodynamic derivatives, and $diag\left\{ {X_{u\left| u \right|} \left| u \right|,Y_{v\left| v \right|} \left| v \right|,Z_{w\left| w \right|} \left| w \right|,K_{p\left| p \right|} \left| p \right|,M_{q\left| q \right|} \left| q \right|,N_{r\left| r \right|} \left| r \right|} \right\}$ is nonlinear cross flow coefficient that can be estimated by calculating the hull drag similar to strip theory.

The gravitational and buoyancy forces and moments, $g\left( \eta \right)$, can be defined as a combined effects of the vehicle’s weight and buoyancy. The vector of gravitational and buoyancy forces and moments are given by

$$g\left( \eta \right) = \left[ {\begin{array}{*{20}c} {\left( {W - B} \right)\sin \theta } \\ { - \left( {W - B} \right)\cos \theta \sin \phi } \\ { - \left( {W - B} \right)\cos \theta \cos \phi } \\ { - \left( {Y_{G} W - Y_{B} B} \right)\cos \theta \cos \phi + \left( {Z_{G} W - Z_{B} B} \right)\cos \theta \sin \phi } \\ {\left( {Z_{G} W - Z_{B} B} \right)\sin \theta + \left( {X_{G} W - X_{B} B} \right)\cos \theta \cos \phi } \\ { - \left( {X_{G} W - X_{B} B} \right)\cos \theta \sin \phi - \left( {Y_{G} W - Y_{B} B} \right)\sin \theta } \\ \end{array} } \right]$$

(49)

Theorem 3

If there exists a continuous function $V\left( \cdot \right):R^{n} \to R^{ + }$ for the continuous system described by Eq. 10 with the following properties: (1) There are scalars $q \ge 1$, $\omega_{1} > 0$ and $\omega_{2} > 0$ such that $\omega_{1} \left\| x \right\|^{q} \le V\left( x \right) \le \omega_{2} \left\| x \right\|^{q}$ for all $x\left( t \right) \in R^{n}$; (2) There are scalars $\bar{V}$ and $\underline{V}$, with $0 \le \underline{V} \le \bar{V} < \infty$, such that whenever $\underline{V} \le V\left( x \right) \le \bar{V}$, $V$ is continuously differentiable and $\dot{V} = \frac{\partial V}{\partial t}f\left( {x,t} \right) \le - q\alpha \left[ {V\left( x \right) - \underline{V} } \right]$ for all $t \in R^{ + }$, then the system (10) is uniformly and exponentially convergent to $S = \varPhi \left( r \right)$ with rate $\alpha$.

The proof was given by Corless and Leitman [29].

Appendix 2: Proof of Theorem 1

Now, let us define the Lyapunov function as follows:

$$V = \frac{1}{2}\tilde{r}^{T} \text{P} \tilde{r} + \frac{1}{2}tr\left( {\tilde{\theta }_{F}^{T} N_{F}^{ - 1} \tilde{\theta }_{F} } \right) + \frac{1}{2}tr\left( {\tilde{\theta }_{G}^{T} N_{G}^{ - 1} \tilde{\theta }_{G} } \right)$$

(50)

Using Eq. 30, the time derivative of $V$ becomes

$$\begin{aligned} \dot{V} = - \frac{1}{2}\tilde{r}^{T} Q\tilde{r} + \tilde{Y}\left( {\tilde{\theta }_{F}^{T} \hat{\bar{\xi }}_{F} + \tilde{\theta }_{G}^{T} \hat{\bar{\xi }}_{G} u + \bar{W}_{F} + \bar{W}_{G} u + \bar{\delta }_{F} + \bar{\varepsilon }_{F} + \bar{\delta }_{G} + \bar{\varepsilon }_{G} u + \bar{\delta } + \bar{\varPhi }_{1} + \bar{\varPhi }_{2} } \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + tr\left( {\tilde{\theta }_{F}^{T} N_{F}^{ - 1} \tilde{\theta }_{F} } \right) + tr\left( {\tilde{\theta }_{G}^{T} N_{G}^{ - 1} \tilde{\theta }_{G} } \right) \hfill \\ \end{aligned}$$

(51)

Substituting the parameter adaptive law (25) and two terms that $\dot{\tilde{\theta }}_{F} = - \dot{\hat{\theta }}_{F}$, $\dot{\tilde{\theta }}_{G} = - \dot{\hat{\theta }}_{G}$ into Eq. (51) yields

$$\begin{aligned} \dot{V} = - \frac{1}{2}\tilde{r}^{T} Q\tilde{r} + \tilde{Y}\left( {\tilde{\theta }_{F}^{T} \hat{\bar{\xi }}_{F} + \tilde{\theta }_{G}^{T} \hat{\bar{\xi }}_{G} u + \bar{W}_{F} + \bar{W}_{G} u + \bar{\delta }_{F} + \bar{\varepsilon }_{F} + \bar{\delta }_{G} + \bar{\varepsilon }_{G} u + \bar{\delta } + \bar{\varPhi }_{1} + \bar{\varPhi }_{2} } \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - tr\left( {\tilde{\theta }_{F}^{T} \hat{\bar{\xi }}_{F} \tilde{Y}} \right) + K_{F} \left\| {\tilde{Y}} \right\|tr\left( {\tilde{\theta }_{F}^{T} \hat{\theta }_{F} } \right){\kern 1pt} {\kern 1pt} - tr\left( {\tilde{\theta }_{G}^{T} \hat{\bar{\xi }}_{G} \tilde{Y}u} \right) + K_{G} \left\| {\tilde{Y}} \right\|tr\left( {\tilde{\theta }_{G}^{T} \hat{\theta }_{G} } \right) \hfill \\ \end{aligned}$$

(52)

Using matrices traces properties $tr\left( {\tilde{\theta }_{F}^{T} \hat{\tilde{\xi }}_{F} \tilde{Y}} \right) = \tilde{Y}\tilde{\theta }_{F}^{T} \hat{\tilde{\xi }}_{F}$ and $tr\left( {\tilde{\theta }_{G}^{T} \hat{\tilde{\xi }}_{G} \tilde{Y}u} \right) = \tilde{Y}\tilde{\theta }_{G}^{T} \hat{\tilde{\xi }}_{G} u$, Eq. 52 can be rewritten as follows:

$$\begin{aligned} \dot{V} = - \frac{1}{2}\tilde{r}^{T} Q\tilde{r} + \tilde{Y}\left( {\bar{W}_{F} + \bar{W}_{G} u + \bar{\delta }_{F} + \bar{\varepsilon }_{F} + \bar{\delta }_{G} + \bar{\varepsilon }_{G} u + \bar{\delta } + \bar{\varPhi }_{1} + \bar{\varPhi }_{2} } \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + K_{F} \left\| {\tilde{Y}} \right\|tr\left( {\tilde{\theta }_{F}^{T} \hat{\theta }_{F} } \right){\kern 1pt} + K_{G} \left\| {\tilde{Y}} \right\|tr\left( {\tilde{\theta }_{G}^{T} \hat{\theta }_{G} } \right) \hfill \\ \end{aligned}$$

(53)

Substituting the following inequalities into Eq. 53

$$\tilde{Y}\left( {\bar{W}_{F} + \bar{\varPhi }_{1} } \right) = \tilde{Y}\left( {\bar{W}_{F} - \rho_{1} \text{sgn} \left( {\tilde{Y}} \right)} \right) \le \left\| {\tilde{Y}} \right\|\left( {\beta_{1} \sigma_{M} - \rho_{1} } \right) \le 0$$

$$\tilde{Y}\left( {\bar{W}_{G} u + \bar{\varPhi }_{2} } \right) = \tilde{Y}\left( {\bar{W}_{G} u - \rho_{2} \text{sgn} \left( {\tilde{Y}} \right)} \right) \le \left\| {\tilde{Y}} \right\|\left( {\beta_{2} \sigma_{M} u_{d} - \rho_{2} } \right) \le 0$$

where $\sigma_{M} = \sigma_{\hbox{max} } \left[ {L^{ - 1} \left( s \right)} \right]$, $\rho_{1} \ge \beta_{1} \sigma_{M}$, $\rho_{2} \ge \beta_{2} \sigma_{M} u_{d}$, yields

$$\begin{aligned} \dot{V} &\le - \frac{1}{2}\lambda_{\hbox{min} } \left( Q \right)\left\| {\tilde{r}} \right\|^{2} + \tilde{Y}\left( {\bar{\delta }_{F} + \bar{\varepsilon }_{F} + \bar{\delta }_{G} + \bar{\varepsilon }_{G} u + \bar{\delta }} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad+ K_{F} \left\| {\tilde{Y}} \right\|tr\left( {\tilde{\theta }_{F}^{T} \hat{\theta }_{F} } \right){\kern 1pt} + K_{G} \left\| {\tilde{Y}} \right\|tr\left( {\tilde{\theta }_{G}^{T} \hat{\theta }_{G} } \right) \hfill \\ \end{aligned}$$

(54)

Using Eq. 28, we can rewrite Eq. 54 as follows:

$$\begin{aligned} \dot{V} \le - \frac{1}{2}\lambda_{\hbox{min} } \left( Q \right)\left\| {\tilde{r}} \right\|^{2} + \left\| {\tilde{Y}} \right\|\left( {\bar{\varepsilon }_{F} + \bar{\varepsilon }_{G} u + \bar{\delta }{ + }D_{F} \left\| {\tilde{\theta }_{F} } \right\|_{F} { + }D_{G} \left\| {\tilde{\theta }_{G} } \right\|_{F} } \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + K_{F} \left\| {\tilde{Y}} \right\|tr\left( {\tilde{\theta }_{F}^{T} \left( {\theta_{F} - \tilde{\theta }_{F} } \right)} \right){\kern 1pt} + K_{G} \left\| {\tilde{Y}} \right\|tr\left( {\tilde{\theta }_{G}^{T} \left( {\theta_{G} - \tilde{\theta }_{G} } \right)} \right) \hfill \\ \end{aligned}$$

(55)

where $\lambda_{\hbox{min} } \left( Q \right)$ represents the smallest eigenvalue of $Q$.

Since $- \lambda_{\hbox{min} } \left( Q \right)\left\| {\tilde{r}} \right\|^{2} \le - \lambda_{\hbox{min} } \left( Q \right)\left\| {\tilde{Y}} \right\|^{2}$, $tr\left[ {\tilde{\theta }^{T} \left( {\theta - \tilde{\theta }} \right)} \right] \le \theta_{M} \left\| {\tilde{\theta }} \right\|_{F} - \left\| {\tilde{\theta }} \right\|_{F}^{2}$, we have

$$\dot{V} \le - \left\| {\tilde{Y}} \right\|\left[ \begin{aligned} \frac{1}{4}\lambda_{\hbox{min} } \left( Q \right)\left\| {\tilde{Y}} \right\| + \frac{1}{4}\lambda_{\hbox{min} } \left( Q \right)\left\| {\tilde{Y}} \right\| - \sigma_{M} \left( {\varepsilon_{F,N} + \varepsilon_{G,N} u_{d} + b_{d} } \right) + K_{F} \left( {\left\| {\tilde{\theta }_{F} } \right\|_{F} - \frac{1}{2}\lambda_{F} } \right)^{2} \hfill \\ - \frac{1}{4}K_{F} \lambda_{F}^{2} + K_{G} \left( {\left\| {\tilde{\theta }_{G} } \right\|_{F} - \frac{1}{2}\lambda_{G} } \right)^{2} - \frac{1}{4}K_{G} \lambda_{G}^{2} \hfill \\ \end{aligned} \right]$$

(56)

where $\lambda_{F} = \theta_{F,M} + \frac{{D_{F} }}{{K_{F} }}$, $\lambda_{G} = \theta_{G,M} + \frac{{D_{G} }}{{K_{G} }}$.

If $\tilde{y}$ lies outside the following compact set $\varOmega_{{\tilde{y}}}$, $\dot{V}$ will be negative.

$$\varOmega_{{\tilde{y}}} = \left\{ {\tilde{Y}\left| {\left\| {\tilde{Y}} \right\| \le \hbox{max} \left\{ {\frac{{4\sigma_{M} \left( {b_{d} + \varepsilon_{F,N} } \right) + K_{F} \lambda_{F}^{2} }}{{\lambda_{\hbox{min} } \left( Q \right)}},\frac{{4\sigma_{M} \varepsilon_{G,N} u_{d} + K_{G} \lambda_{G}^{2} }}{{\lambda_{\hbox{min} } \left( Q \right)}}} \right\}} \right.} \right\}$$

(57)

Based on the standard Lyapunov theorem (see [28]), one can conclude that $\tilde{Y}$ will converge to $\varOmega_{{\tilde{Y}}}$. Furthermore, the radius of $\varOmega_{{\tilde{Y}}}$ can be designed arbitrarily small if $K_{F} ,K_{G}$ are chosen to be sufficiently small.

One can also guarantee that $\dot{V}$ is negative when the parameter adaptive error vectors $\tilde{\theta }_{G}$ and $\tilde{\theta }_{F}$ are bounded and converge to $\varOmega_{{\tilde{\theta }_{G} }}$ and $\varOmega_{{\tilde{\theta }_{F} }}$, which are defined as follows:

$$\varOmega_{{\tilde{\theta }_{F} }} = \left\{ {\tilde{\theta }_{F} \left| {\left\| {\tilde{\theta }_{F} } \right\| \le \frac{1}{2}\lambda_{F} { + }\sqrt {\frac{{\sigma_{M} \left( {b_{d} + \varepsilon_{F,N} } \right)}}{{K_{F} }}{ + }\frac{{\lambda_{F}^{2} }}{4}} } \right.} \right\}$$

(58)

$$\varOmega_{{\tilde{\theta }_{G} }} = \left\{ {\tilde{\theta }_{G} \left| {\left\| {\tilde{\theta }_{G} } \right\| \le \frac{1}{2}\lambda_{G} { + }\sqrt {\frac{{\sigma_{M} \varepsilon_{G,N} u_{d} }}{{K_{G} }}{ + }\frac{{\lambda_{G}^{2} }}{4}} } \right.} \right\}$$

(59)

The tracking error Eq. 19 can also be rewritten as follows:

$$\dot{\tilde{X}} = \left( {A - KC^{T} } \right)\tilde{X} + B\tilde{u}$$

(60)

where $\tilde{u} = \tilde{\theta }_{F}^{T} \hat{\xi }_{F} + \tilde{\theta }_{G}^{T} \hat{\xi }_{G} u + C$ with $C = W_{F} + \varepsilon_{F} + \varPhi_{ 1} + \left( {W_{G} + \varepsilon_{G} } \right)u + \delta + \varPhi_{2}$. Using the Lemma 1, Eq. 60 can be expressed as

$$\left\| X \right\| \le K_{1} + K_{2} \left\| {\tilde{u}} \right\|_{2}^{\alpha }$$

(61)

Using the following inequalities

$$\left\| {\tilde{\theta }_{F}^{T} \hat{\xi }_{F} } \right\|_{2}^{\alpha } \le \left\| {\tilde{\theta }_{F}^{T} } \right\|_{F}^{\alpha } \sqrt {\int_{0}^{t} {e^{{ - a\left( {t - \tau } \right)}} \hat{\xi }_{F} \hat{\xi }_{F}^{T} d\tau } } = \left\| {\tilde{\theta }_{F}^{T} } \right\|_{F}^{\alpha } \left\| {\hat{\xi }_{F} } \right\|\frac{1}{\sqrt a }\sqrt {1 - e^{ - at} } \le \left\| {\tilde{\theta }_{F}^{T} } \right\|_{F}^{\alpha } \frac{1}{\sqrt a }S_{5}^{1}$$

$$\left\| {\tilde{\theta }_{G}^{T} \hat{\xi }_{G} } \right\|_{2}^{\alpha } \le \left\| {\tilde{\theta }_{G}^{T} } \right\|_{F}^{\alpha } \sqrt {\int_{0}^{t} {e^{{ - a\left( {t - \tau } \right)}} \hat{\xi }_{G} \hat{\xi }_{G}^{T} d\tau } } = \left\| {\tilde{\theta }_{G}^{T} } \right\|_{F}^{\alpha } \left\| {\hat{\xi }_{G} } \right\|\frac{1}{\sqrt a }\sqrt {1 - e^{ - at} } \le \left\| {\tilde{\theta }_{G}^{T} } \right\|_{F}^{\alpha } \frac{1}{\sqrt a }S_{6}^{1}$$

where $S_{5}^{1} = \left\| {\hat{\xi }_{F} } \right\|\sqrt {1{ - }e^{ - at} }$, $S_{6}^{1} = \left\| {\hat{\xi }_{G} } \right\|\sqrt {1{ - }e^{ - at} }$, $\left\| C \right\|_{2}^{\alpha } \le S_{4}^{1}$, one can obtain

$$\left\| X \right\| \le S_{1} { + }\left( {S_{2} \left\| {\tilde{\theta }_{F}^{T} } \right\|_{F}^{\alpha } + S_{3} \left\| {\tilde{\theta }_{G}^{T} } \right\|_{F}^{\alpha } } \right)\frac{1}{\sqrt a }$$

(62)

where $S_{1} = K_{1} + K_{2} S_{4}^{1}$, $S_{2} = K_{2} S_{5}^{1}$, $S_{3} = K_{2} S_{6}^{1}$.

From the inequalities (58) and (59), the state estimation error $\left\| {\tilde{x}} \right\|$ is limited by the two bounded weight estimation errors $\left\| {\tilde{\theta }_{F}^{T} } \right\|_{F}^{\alpha }$ and $\left\| {\tilde{\theta }_{G}^{T} } \right\|_{F}^{\alpha }$. This proof is completed.

Appendix 3: Proof of Theorem 2

Now, let us design the following Lyapunov function:

$$V = \frac{1}{2}\chi_{e}^{T} P_{c} \chi_{e} + \frac{1}{2}\sum\limits_{i = 1}^{M} {\frac{1}{{\gamma_{i} }}\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \tilde{\theta }_{i} }$$

(63)

where $\gamma_{i} \in \left[ {0, + \infty } \right]$, $\chi_{e} = \left[ {e,\dot{e}} \right]^{T}$,$\varGamma_{i}^{ - 1} = {\text{diag}}\left\{ {l_{1}^{ - 1} ,l_{2}^{ - 1} , \ldots ,l_{M}^{ - 1} } \right\}$, $\tilde{\theta }_{i} = \hat{\theta }_{i} - \theta_{i}$.Let $V_{1} = \frac{1}{2}\chi_{e}^{T} P_{c} \chi_{e}$ and $V_{2} = \frac{1}{2}\sum\limits_{i = 1}^{M} {\frac{1}{{\gamma_{i} }}\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \tilde{\theta }_{i} }$. Differentiating $V_{1}$ along the tracking error dynamic Eq. 36 and using the Riccati-like Eq. 39, one can obtain

$$\dot{V}_{1} = \frac{1}{2}\chi_{e}^{T} \left( {A_{c}^{T} P_{c} + P_{c} A_{c} } \right)\chi_{e} + x_{e}^{T} P_{c} B_{c} \psi - x_{e}^{T} P_{c} B_{c} \phi_{f}$$

(64)

Now, using the boundaries of the uncertainties in Assumption 1 and $\phi_{f} = \phi_{1} + K_{D} \phi_{2} + K_{P} \phi_{3}$, we can get

$$\begin{aligned} \dot{V}_{1} \le \frac{1}{2}\chi_{e}^{T} \left( {A_{c}^{T} P_{c} + P_{c} A_{c} } \right)\chi_{e} + \left[ {\left\| {\theta_{1}^{T} \xi \left( {x_{d} } \right)} \right\| + K_{D} \left\| {\theta_{2}^{T} \xi \left( {x_{d} } \right)} \right\| + K_{P} \left\| {\theta_{3}^{T} \xi \left( {x_{d} } \right)} \right\|} \right]\left\| {\chi_{e}^{T} P_{c} B_{c} } \right\| \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \chi_{e}^{T} P_{c} B_{c} \left[ {\phi_{1} + K_{D} \phi_{2} + K_{P} \phi_{3} } \right] \\ \end{aligned}$$

(65)

Substituting Eq. 37 into Eq. 65 yields

$$\begin{aligned} \dot{V}_{1} \le \frac{1}{2}\chi_{e}^{T} \left( {A_{c}^{T} P_{c} + P_{c} A_{c} } \right)\chi_{e} + \left[ {\left\| {\hat{\theta }_{1}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c} } \right\|{ - }\chi_{e}^{T} P_{c} B_{c} \hat{\theta }_{1}^{T} \xi \left( {x_{d} } \right)\tanh \left( {\frac{{\hat{\theta }_{1}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} x_{d} }}{\varepsilon }} \right)} \right] \\ { + }K_{D} \left[ {\left\| {\hat{\theta }_{2}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c} } \right\|{ - }\chi_{e}^{T} P_{c} B_{c} \hat{\theta }_{2}^{T} \xi \left( {x_{d} } \right)\tanh \left( {\frac{{\hat{\theta }_{2}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} x_{d} }}{\varepsilon }} \right)} \right] \\ { + }K_{P} \left[ {\left\| {\hat{\theta }_{p}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c} } \right\|{ - }\chi_{e}^{T} P_{c} B_{c} \hat{\theta }_{p}^{T} \xi \left( {x_{d} } \right)\tanh \left( {\frac{{\hat{\theta }_{p}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} x_{d} }}{\varepsilon }} \right)} \right] \\ - \left[ {\left\| {\tilde{\theta }_{1}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c} } \right\| + K_{D} \left\| {\tilde{\theta }_{2}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c} } \right\| + K_{P} \left\| {\tilde{\theta }_{3}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c} } \right\|} \right] \\ \end{aligned}$$

(66)

Let $\eta_{1} = \hat{\theta }_{1}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c}$, $\eta_{2} = \hat{\theta }_{2}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c}$ and $\eta_{3} = \hat{\theta }_{3}^{T} \xi \left( {x_{d} } \right)\chi_{e}^{T} P_{c} B_{c}$. Using Lemma 2, the following inequalities can be obtained: $\left| {\eta_{i} } \right| - \eta_{i} \tanh \left( {\frac{{\eta_{i} }}{\varepsilon }} \right) \le \kappa_{i} \varepsilon_{i}$. Therefore, Eq. 66 becomes

$$\begin{aligned} \dot{V}_{1} \le \frac{1}{2}\chi_{e}^{T} \left( {A_{c}^{T} P_{c} + P_{c} A_{c} } \right)\chi_{e} + \kappa \varepsilon \\ - \left[ {\tilde{\theta }_{1}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} \chi_{e} + K_{D} \tilde{\theta }_{2}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} \chi_{e} + K_{P} \tilde{\theta }_{3}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} \chi_{e} } \right] \\ \end{aligned}$$

(67)

where $\kappa \varepsilon = \kappa_{1} \varepsilon_{1} { + }K_{D} \kappa_{2} \varepsilon_{2} { + }K_{P} \kappa_{3} \varepsilon_{3}$.

Then, differentiating $V_{2}$ in Eq. 63 along the tracking error dynamic Eq. 36, and using the adaptive law (38), one can obtain

$$\dot{V}_{2} = \sum\limits_{i = 1}^{M} {\left[ {{ - }\frac{{\lambda_{i} }}{{\gamma_{i} }}\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \left( {\tilde{\theta }_{i} { + }\theta_{i} } \right){ + }\frac{1}{{\gamma_{i} }}\tilde{\theta }_{i}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} \chi_{e} } \right]}$$

(68)

Since $\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \tilde{\theta }_{i} { + }\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \theta_{i} \ge \frac{1}{2}\left( {\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \tilde{\theta }_{i} - \theta_{i}^{T} \varGamma_{i}^{ - 1} \theta_{i} } \right)$, Eq. 68 can be arranged

$$\dot{V}_{2} \le \sum\limits_{i = 1}^{M} {\left[ {{ - }\frac{{\lambda_{i} }}{{2\gamma_{i} }}\left( {\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \tilde{\theta }_{i} { - }\theta_{i}^{T} \varGamma_{i}^{ - 1} \theta_{i} } \right){ + }\frac{1}{{\gamma_{i} }}\tilde{\theta }_{i}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} \chi_{e} } \right]}$$

(69)

From Eqs. 67 and 69, one can obtain the following boundedness of the time-derivative of the Lyapunov function:

$$\begin{aligned} \dot{V} \le \frac{1}{2}\chi_{e}^{T} \left( {A_{c}^{T} P_{c} + P_{c} A_{c} } \right)\chi_{e} + \kappa \varepsilon - K_{\hbox{min} } \sum\limits_{i = 1}^{M} {\left( {\tilde{\theta }_{i}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} \chi_{e} } \right)} \\ { + }\sum\limits_{i = 1}^{M} {\left( { - \frac{{\lambda_{i} }}{{2\gamma_{i} }}\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \tilde{\theta }_{i} } \right){ + }\sum\limits_{i = 1}^{M} {\left( {\frac{{\lambda_{i} }}{{2\gamma_{i} }}\theta_{i}^{T} \varGamma_{i}^{ - 1} \theta_{i} } \right)} { + }\sum\limits_{i = 1}^{M} {\left( {\frac{1}{{\gamma_{i} }}\tilde{\theta }_{i}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} \chi_{e} } \right)} } \\ \end{aligned}$$

(70)

where $K_{\hbox{min} } = \hbox{min} \left\{ {1,K_{D} ,K_{P} } \right\}$.

Using Lemma 3, one can obtain the following inequality:$\tilde{\theta }_{i}^{T} \xi \left( {x_{d} } \right)B_{c}^{T} P_{c} \chi_{e} \le \frac{1}{2}\left[ {\delta \tilde{\theta }_{i}^{T} \xi \left( {x_{d} } \right)\xi \left( {x_{d} } \right)^{T} \tilde{\theta }_{i} + \delta^{ - 1} \chi_{e}^{T} P_{c} B_{c} B_{c}^{T} P_{c} \chi_{e} } \right]$, where $\delta$ is an arbitrarily small positive constant. Substituting the inequality into Eq. 70 yields

$$\begin{aligned} \dot{V} \le \frac{1}{2}\chi_{e}^{T} \left( {A_{c}^{T} P_{c} + P_{c} A_{c} { + }\delta^{ - 1} \sum\limits_{i = 1}^{M} {\left( {\frac{1}{{\gamma_{i} }} - K_{\hbox{min} } } \right)P_{c} B_{c} B_{c}^{T} P_{c} } } \right)\chi_{e} + \kappa \varepsilon \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} { + }\sum\limits_{i = 1}^{M} {\left( {\left( {{ - }\frac{{\lambda_{i} }}{2}{ + }\frac{\delta }{{2\varGamma_{i}^{ - 1} }}\left( {1 - \gamma_{i} K_{\hbox{min} } } \right)\xi \left( {x_{d} } \right)\xi \left( {x_{d} } \right)^{T} } \right)\frac{1}{{\gamma_{i} }}\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \tilde{\theta }_{i} } \right)} { + }\sum\limits_{i = 1}^{M} {\left( {\frac{{\lambda_{i} }}{{2\gamma_{i} }}\theta_{i}^{T} \varGamma_{i}^{ - 1} \theta_{i} } \right)} \\ \end{aligned}$$

(71)

Substituting the Riccati-like Eq. 39 into Eq. 71 yields

$$\begin{aligned} \dot{V} \le - \frac{1}{2}\frac{{\lambda_{\hbox{min} } \left( {Q_{c} } \right)}}{{\lambda_{\hbox{max} } \left( {P_{c} } \right)}}\chi_{\varepsilon }^{T} P_{c} \chi_{\varepsilon } + \frac{1}{2}\sum\limits_{i = 1}^{M} {\left( {\left( {{ - }\lambda_{i} { + }\frac{\delta }{{\varGamma_{i}^{ - 1} }}\left( {1 - \gamma_{i} K_{\hbox{min} } } \right)\xi \left( {x_{d} } \right)\xi \left( {x_{d} } \right)^{T} } \right)\frac{1}{{\gamma_{i} }}\tilde{\theta }_{i}^{T} \varGamma_{i}^{ - 1} \tilde{\theta }_{i} } \right)} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \kappa \varepsilon { + }\sum\limits_{i = 1}^{M} {\left( {\frac{{\lambda_{i} }}{{2\gamma_{i} }}\theta_{i}^{T} \varGamma_{i}^{ - 1} \theta_{i} } \right)} \\ \le - \mu V + \sigma \\ \end{aligned}$$

(72)

where $\mu = \hbox{min} \left\{ {\frac{{\lambda_{\hbox{min} } \left( {Q_{c} } \right)}}{{\lambda_{\hbox{max} } \left( {P_{c} } \right)}},\lambda_{i} { + }\frac{\delta }{{\varGamma_{i}^{ - 1} }}\left( {\gamma_{i} K_{\hbox{min} } - 1} \right)\xi \left( {x_{d} } \right)\xi \left( {x_{d} } \right)^{T} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {i = 1,2, \cdots ,M} \right)} \right\}$, $\sigma = \kappa \varepsilon { + }\sum\limits_{i = 1}^{M} {\left( {\frac{{\lambda_{i} }}{{2\gamma_{i} }}\theta_{i}^{T} \varGamma_{i}^{ - 1} \theta_{i} } \right)}$.

Since $\omega_{1} \left( {\left\| {\chi_{e} } \right\|^{2} + \sum\limits_{i = 1}^{M} {\left\| {\tilde{\theta }_{i} } \right\|^{2} } } \right) \le V\left( x \right) \le \omega_{2} \left( {\left\| {\chi_{e} } \right\|^{2} + \sum\limits_{i = 1}^{M} {\left\| {\tilde{\theta }_{i} } \right\|^{2} } } \right)$, in which $\omega_{1} = \frac{1}{2}\hbox{min} \left( {\lambda_{\hbox{min} } \left( {P_{c} } \right),\sum\limits_{i = 1}^{M} {\frac{1}{{\gamma_{i} }}\lambda_{\hbox{min} } \left( {\varGamma_{i}^{ - 1} } \right)} } \right)$ and $\omega_{2} = \frac{1}{2}\hbox{max} \left( {\lambda_{\hbox{max} } \left( {P_{c} } \right),\sum\limits_{i = 1}^{M} {\frac{1}{{\gamma_{i} }}\lambda_{\hbox{max} } \left( {\varGamma_{i}^{ - 1} } \right)} } \right)$, $V\left( x \right)$ satisfies the first property in the Theorem 3 in “Appendix 1”. Furthermore, we can obtain the second property $\dot{V} \le - q\alpha \left[ {V - \underline{V} } \right]$, where $q = 2$, $\alpha = \frac{1}{2}\mu$. Therefore, using the Theorem 3, it can be seen that the tracking error converges towards a residual set $\varPhi \left( r \right)$ with the convergence rate ${\raise0.7ex\hbox{$\mu $} \!\mathord{\left/ {\vphantom {\mu 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}$.