1 Introduction

Broaching is a phenomenon in which a ship cannot maintain a constant course despite the maximum steering effort being applied. Broaching often occurs when a ship is surf ridden on the downslope of a stern-quartering wave, which induces significant yaw moment. The centrifugal forces resulting from this violent yaw motion can result in capsizing. This presents a real threat to high-speed vessels such as destroyers, high-speed RoPax ferries, and fishing vessels.

To prevent stability failure due to the broaching associated with surf riding, the International Maritime Organization (IMO decided to develop new physics-based stability criteria to be added to the 2008 Intact Stability Code [1]. They comprised two levels of vulnerability criteria based on simplified physical models with a given safety margin and combined with direct stability assessment using numerical simulation to quantify the probability of stability failure in irregular waves.

The IMO vulnerability criteria were based on surf riding rather than broaching [2]. Surf riding was known to be a precondition for broaching in ship stability failure. Because broaching requires the maneuvering elements to be considered, its use was judged too complicated to be practicable. At the higher-level vulnerability criterion, the probability of surf riding in the North Atlantic was estimated using a global bifurcation analysis and a stochastic wave theory. If the estimated probability was larger than the acceptable safety level, the ship was judged to be vulnerable to surf riding. At its lower level, to avoid explicit use of the surf riding probability, a wave steepness of 1/10 was assumed as the physical upper limit at sea. This allowed the critical Froude number to be determined as 0.3. These were adopted in IMO operational guidance MSC/Circ. 707 [3] as amended by MSC.1/Circ. 1228, and the vulnerability criteria were agreed in principle by the sub-committee on Ship Design and Construction in 2015 [4].

The issue of direct stability assessment has not yet been fully resolved by the IMO. It requires the quantification of the probability of broaching under maneuvering in irregular waves, and it is unclear whether current methodologies in ship dynamics can evaluate the probability of broaching sufficiently accurately within a practical calculation time. The major problem is that broaching is a nonlinear phenomenon. A mathematical model of broaching has not yet been fully established, and linear superposition techniques are not adequate to apply. In this paper, we attempt to provide positive and rigid answers to this question.

Scientific research on broaching can be traced back to Davidson [5], similar to researches on ship maneuverability, in 1940s. Davidson investigated the directional stability of ships in following waves using a linear sway–yaw-coupled model, and treated wave-induced forces as the sum of Froude–Krylov forces and the hydrodynamic lift caused by wave particle velocity. He reported that even directionally stable ships can become directionally unstable on the downslope of waves. Wahab and Swaan [6] pursued this approach further, but using only the Froude Krylov components. Eda [7] proposed a surge–sway–yaw-coupled model for solving the linear stability problem.

In 1982, Motora et al. [8] and Renilson [9] numerically integrated nonlinear equations of surge–sway–yaw motions and concluded that a necessary condition for broaching under surf riding is that the wave-induced yaw moment exceeds the maximum yaw moment supplied by steering. Hamamoto and Akiyoshi [10] and de Kat and Paulling [11] in late 1980s independently developed 6 DOF mathematical models combining strip theory and maneuvering models for capsizing and broaching. Umeda and Renilson [12] developed a 4 DOF mathematical model based on a maneuvering model with roll coupling and linear wave forces under low-encounter frequency assumption. Assuming that wave steepness and maneuvering motions are small, all higher-order terms such as interactions due to maneuvering and waves can be neglected. Umeda and Hashimoto [13] reported that this mathematical model showed qualitative agreement with free-running model experiments using a single-propeller and single-rudder fishing vessel. The International Towing Tank Conference (ITTC) specialist committee on extreme motions and capsizing conducted a benchmark testing study of numerical models with the same model test data and concluded that some numerical approaches can qualitatively predict the occurrence of broaching [14].

To make prediction quantitative, it is necessary to take higher-order terms into account in the mathematical model. Umeda et al. [15] and Hashimoto et al. [16] developed a mathematical model with second-order terms taken into account and derived quantitative prediction for a fishing vessel. Potential flow theories and captive model experiments were used to estimate hydrodynamic forces arising from the interaction between maneuvering and waves; hydrodynamic forces due to the large roll angle, nonlinear wave, and maneuvering forces; and other factors.

However, the establishment of an accurate mathematical model of broaching in regular waves is not the goal of ship dynamics, because the phenomenon itself is nonlinear, making the results sensitive to initial conditions. Techniques based on nonlinear dynamical system theory are required. Such an approach was first applied to surf riding bifurcation of an uncoupled surge motion. Grim [17] explained that the surf riding boundary coincides with the trajectory from an unstable equilibrium of an uncoupled surge model on a wave to another unstable equilibrium. This is a heteroclinic bifurcation in the terminology of nonlinear dynamical system theory. Makov [18] confirmed Grim’s theory using phase plane analysis. He found that surf riding of a self-propelled ship occurs regardless of the initial condition in the phase plane, at the heteroclinic bifurcation. Ananiev [19] obtained an analytically approximated solution by applying a perturbation technique. Spyrou [20] presented an exact analytical solution of the heteroclinic bifurcation of an uncoupled surge model under conditions of quadratic calm-water resistance. In 1990 Kan [21] applied the Melnikov analysis to an uncoupled surge model having a locally linear calm-water resistance curve, and Spyrou [22] did the same with a linear quadratic cubic calm-water resistance curve. Maki et al. [23, 24] provided formulae for calm-water resistance curves as general polynomials for lower and upper surf riding thresholds, and validated them with numerical bifurcation analysis and a free-running model experiment.

Umeda and Renilson [25] extended the nonlinear dynamical system approach from an uncoupled surge model to a coupled surge–sway–yaw model. Spyrou [26, 27] and Umeda [28] numerically obtained a heteroclinic bifurcation for the uncoupled surge model and the coupled surge–sway–yaw–roll model with a PD autopilot, respectively. Umeda et al. [29] and Maki et al. [30] applied numerical bifurcation analysis to the coupled model and validated the results using experiments with a fishing vessel model. The results confirmed the existence of distinct initial condition dependence in the occurrence of broaching, but only if the initial condition was set above the periodic states for self-propelled ships. This allows the initial condition dependence to be disregarded in both numerical simulations and free-running model experiments.

All these studies investigated broaching in single-propeller and single-rudder ships. Since most destroyers and high-speed RoPax ferries have twin propellers and twin rudders, broaching for such vessels must be investigated. Umeda et al. [31] reported that the methodology used for single-propeller and single-rudder ships was inapplicable to twin-propeller and twin-rudder ships because a large roll due to broaching could result in the surfacing of a propeller and/or a rudder. Hashimoto et al. [32] used a simplified modification of rudder emergence to model twin-propeller and twin-rudder ships, but a more comprehensive approach is needed. Umeda et al. [33] measured rudder normal forces during broaching in free-running model experiments. The measured rudder normal forces agreed reasonably well with numerical simulation, and the effect of rudder emergence significantly improved prediction accuracy for broaching. Note here that Sadat-Hosseini et al. [34] applied computational fluid dynamics (CFD) to the broaching of a twin-propeller and twin-rudder ship in regular waves, and compared the results with a free-running model experiment. Since this approach requires tremendous computational resources even for regular waves, its direct application to regulations is impractical, so system identification techniques were applied to the CFD results to improve the 6 DOF mathematical model [35].

For regulatory purposes, the danger of broaching in irregular waves also needs to be assessed. Rutgerssen and Ottosson [36] and Motora et al. [8] executed model experiments in irregular waves in a seakeeping and maneuvering basin, and undertook real full-scale measurements at sea. However, the probabilistic aspects of broaching were not addressed. As the probabilistic modeling of broaching in irregular waves is indispensable for practical applications, Umeda [37], in 1990, proposed a theoretical method for estimating surf riding probability in irregular waves, using a deterministic surf riding threshold and the joint probability of local wave heights and wave periods. Umeda et al. [38] extended this methodology to broaching, and successfully validated it using Monte Carlo simulation in a time domain. However, the results have not yet been experimentally confirmed. Themelis and Spyrou [39] proposed a similar methodology without attempting experimental validation.

We have therefore attempted to validate the probabilistic methodology proposed by Umeda et al. [38], by conducting free-running model experiments in irregular waves. The subject ship used was an ONR flared topside vessel, representing a typical high-speed, twin-propeller and twin-rudder ship. The mathematical model was updated for twin-propeller and twin-rudder ships based on our previous literature.

2 Estimation method for broaching probability

To estimate the probability of surf riding and/or broaching in irregular waves, one of the authors [37, 38] has proposed a theoretical method based on a combination of deterministic nonlinear ship dynamics and a probabilistic wave theory. Real ocean waves are clearly irregular and can be regarded as a sequence of local sinusoidal waves defined between the zero crossing of water elevation. Each local wave has a wave height and a wavelength. Broaching associated with surf riding normally occurs within one or two waves as the ship is captured, and violently turned, by a wave downslope. Thus, the occurrence of broaching can be estimated from the local wave that the ship encounters and the initial conditions of ship motion. For addressing surf riding probability, both local wave and initial conditions were taken into account [37], while broaching probability was successfully validated using Monte Carlo simulation [38] without considering the effect of initial conditions. In this research, we first attempted to validate the method without taking into account the initial condition effect.

The broaching probability that this paper deals with is the conditional probability when a ship meets a zero-crossing wave. This probability, P, can be approximately calculated as the probability of encountering a local wave that causes broaching, so that can be formulated as follows [38]:

$$ P = \iint_{S(l,s)} {p^{*} }(l,s){\text{d}}l{\text{d}}s, $$
(1)

where l and s represent the local wavelength to ship length ratio and local wave steepness, respectively. The function p *(l, s) is a joint-probability density function of local wavelength to ship length ratio and local wave steepness. S is the region in which a ship suffers broaching in local waves.

In the draft IMO regulation [2], Eq. 1 is represented in the following discretized form:

$$ P = \sum\limits_{i} {\sum\limits_{j} {C\left( {l_{i} ,s_{j} } \right)p^{*} \left( {l_{i} ,s_{j} } \right)\Delta l\Delta s} } , $$
(2)

where

$$ C\left( {l_{i} ,s_{j} } \right) = \left\{ {\begin{array}{*{20}l} {1\quad {\text{if}}\quad {\text{broaching}}\,{\text{occurs}}} \\ {0\quad {\text{if}}\quad {\text{broaching}}\,{\text{does not}}\,{\text{occur}}} \\ \end{array} } \right. $$
(3)

C(l i , s j ) is obtained using a time-domain numerical simulation in regular waves having the i-th wavelength to ship length ratio and the j-th wave steepness. If the significant wave height H 1/3 and the mean wave period T 01 are known, a joint-probability density function p *(l i , s j ) for the i-th local wavelength to ship length ratio and the j-th local wave steepness can be calculated by applying Longuet–Higgins’ theory [40], as follows:

$$ \begin{aligned} p^{*} \left( {l_{i} ,s_{j} } \right) &= \frac{4\sqrt g }{\pi \nu }\frac{{L^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} T_{01} }}{{\left( {H_{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} } \right)^{3} }}s_{j}^{2} l_{i}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \left( {\frac{{\sqrt {1 + \nu^{2} } }}{{1 + \sqrt {1 + \nu^{2} } }}} \right) \hfill \\ &\quad\times \;\exp \left[ { - 2\left( {\frac{{Ll_{i} s_{j} }}{{H_{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }}} \right)^{2} \left\{ {1 + \frac{1}{{\nu^{2} }}\left( {1 - \sqrt {\frac{{gT_{01}^{2} }}{{2\pi l_{i} L}}} } \right)^{2} } \right\}} \right], \hfill \\ \end{aligned} $$
(4)

where ν (=0.4256) is the band parameter for a Pierson–Moskowitz spectrum. This is based on the wave envelope theory and has been reasonably well validated with field measurement data.

For determining S or C, we used a coupled surge–sway–yaw–roll time-domain simulation model in regular waves with an autopilot and then counted the number of occurrences of broaching in the time series obtained. In this process, we needed a criterion to judge whether broaching had occurred. Since broaching is known to mariners as the loss of straight run despite maximum steering efforts, we mathematically simulated this situation using the following criteria [41]:

$$ \begin{aligned} \delta &= \delta_{\hbox{max} } ,\quad r < 0,\quad \dot{r} < 0 \hfill \\ {\text{or}} \hfill \\ \delta &= - \delta_{\hbox{max} } ,\quad r > 0,\quad \dot{r} > 0, \hfill \\ \end{aligned} $$
(5)

where r is yaw angular velocity and δ is the rudder angle. Here, we regarded applying the maximum rudder deflection δ max as the maximum steering effort. If the ship yaw angular velocity increases in the opposite direction, this can regarded as broaching. This criterion was used in both model experiments and numerical simulations.

To obtain reliable values of broaching probability, the broaching region S should be defined as accurately as possible, making validation of the time-domain numerical simulation in regular waves indispensable. This will be discussed in the following chapters.

3 Configuration of the ONR flare topside vessel

As noted, an ONR flare topside vessel was used as the subject ship. While Hashimoto et al. [32] used the ONR tumblehome topside vessel, the ONR flare topside vessel can be used to represent conventional high-speed monohull ships, as it has twin propellers and twin rudders. A body plan of the subject ship is shown in Fig. 1 and the details of the ship are given in the “Appendix”.

Fig. 1
figure 1

Body plan of the ONR flare topside vessel

Full size image

For the model experiments, a ship model with a scale of 1/46.60 was used.

4 Time-domain numerical simulation model

4.1 Mathematical model

To understand the broaching phenomenon in regular waves, a numerical simulation model based on a coupled surge–sway–yaw–roll maneuvering model with linear wave force and nonlinear restoring variations was used, following Umeda and Hashimoto [42]. Maneuvering, roll damping, and propulsion coefficients were determined using conventional model tests, such as CMT in calm water. Linear wave force was estimated by applying the slender body theory with very low encounter frequencies [43].

Since ships running in following and stern-quartering waves at high forward speeds have low encounter frequencies, a maneuvering-based mathematical model of surge–sway–yaw–roll motion was developed with linear wave-induced forces and a PD autopilot to simulate the broaching associated with surf riding. This is referred to as the “original model.” Based on the original model, we developed a mathematical model to predict broaching of twin-propeller and twin-rudder ships running in following and stern-quartering waves. The wave steepness was assumed to be much smaller than one. Drift angle and yaw angular velocity, normalized for a ship length and a forward speed, and rudder angle were also regarded as small because they are induced by waves. The interaction terms of these elements could therefore be disregarded in a first-order approximation, and hence the maneuvering coefficients did not depend on waves. Roll angle could not be treated as negligible because it is an essential element in predicting a capsize. Propeller thrust, which can be represented by constant linear and quadratic terms of advanced coefficient, could also not be treated as negligible because it includes terms that are proportional to wave steepness. Side force induced by propellers operating in non-axial inflow was neglected, because drift motion during broaching is of minor significance. Based on these assumptions, higher-order terms of heel-induced hydrodynamic forces, wave effect on roll-restoring moment, and wave effect on propeller thrust were taken into account in the mathematical model. As the original model was developed for ships with a single propeller and a single rudder, it was extended to ships with twin propellers and twin rudders following Lee et al. [44] and Furukawa et al. [45]. Propeller thrust and rudder force were presumed to be proportional to the submerged surface area of the propellers and rudders. Both rudders underwent the same deflection, following the proportional control of the autopilot. Since the wave particle velocity at each propeller position was taken into account as the change in inflow velocity when estimating thrust variation, the turning moment produced by the difference in thrust of the two propellers could be calculated.

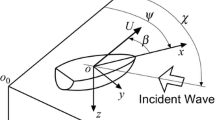
The coordinate systems are shown in Fig. 2. A space-fixed coordinate system O-ξηζ has its origin at a wave trough. A body-fixed system G-x′y′z′ has its origin at the center of gravity of the ship. A horizontal body G-xyz coordinate system [46] also has its origin at the center of gravity and does not rotate around the x-axis and y-axis.

Fig. 2
figure 2

Coordinate systems

Full size image

The space-fixed coordinate system and the body-fixed system have the following relationship:

$$ \left( {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \theta } & {\sin \varphi \;\sin \theta } & {\cos \varphi \;\sin \theta } \\ 0 & {\cos \varphi } & { - \sin \varphi } \\ { - \sin \theta } & {\sin \varphi \;\cos \theta } & {\cos \varphi \;\cos \theta } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {x'} \\ {y'} \\ {z'} \\ \end{array} } \right), $$
(6)
$$ \left( {\begin{array}{*{20}c} {x'} \\ {y'} \\ {z'} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \theta \;\cos \chi } & {\cos \theta \;\sin \chi } & { - \sin \theta } \\ {\sin \varphi \;\sin \theta \;\cos \chi - \cos \varphi \;\sin \chi } & {\sin \varphi \;\sin \theta \;\sin \chi + \cos \varphi \;\cos \chi } & {\sin \varphi \;\cos \theta } \\ {\cos \varphi \;\sin \theta \;\cos \chi + \sin \varphi \;\sin \chi } & {\cos \varphi \;\sin \theta \;\sin \chi - \sin \varphi \;\cos \chi } & {\cos \varphi \;\cos \theta } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\xi - \xi_{G} } \\ {\eta - \eta_{G} } \\ {\zeta - \zeta_{G} } \\ \end{array} } \right). $$
(7)

Based on the coordinate systems, the state vector x and control vector b of the system are defined as follows:

$$ {\mathbf{x}} = \left( {x_{1} ,x_{2} , \ldots ,x_{8} } \right)^{\text{T}} = \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },u,v,\chi ,r,\varphi ,p,\delta } \right)^{\text{T}} , $$
(8)
$$ {\mathbf{b}} = \left( {n,\chi_{C} } \right)^{\text{T}} . $$
(9)

The dynamical system can be represented by the following state equation:

$$ {\dot{\mathbf{x}}} = {\mathbf{F}}\left( {{\mathbf{x}};{\mathbf{b}}} \right) = \left\{ {f_{1} \left( {{\mathbf{x}};{\mathbf{b}}} \right),f_{2} \left( {{\mathbf{x}};{\mathbf{b}}} \right), \ldots ,f_{8} \left( {{\mathbf{x}};{\mathbf{b}}} \right)} \right\}^{\text{T}} , $$
(10)

where

$$ f_{1} \left( {{\mathbf{x}};{\mathbf{b}}} \right) = (u\cos \chi - v\sin \chi - c )/{\lambda}, $$
(11)
$$ f_{2} \left( {{\mathbf{x}};{\mathbf{b}}} \right) = {{\left\{ {T\left( {\xi_{G} ,\zeta_{G} ,u,\varphi ,\theta ,\chi ,t;n} \right) - R\left( u \right) + X_{W} \left( {\xi_{G} ,\chi ,t} \right) + X_{R} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\zeta_{G} ,u,\varphi ,\theta ,\chi ,\delta ;n} \right)} \right\}} \mathord{\left/ {\vphantom {{\left\{ {T\left( {\xi_{G} ,\zeta_{G} ,u,\varphi ,\theta ,\chi ,t;n} \right) - R\left( u \right) + X_{W} \left( {\xi_{G} ,\chi ,t} \right) + X_{R} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\zeta_{G} ,u,\varphi ,\theta ,\chi ,\delta ;n} \right)} \right\}} {\left( {m + m_{x} } \right)}}} \right. \kern-0pt} {\left( {m + m_{x} } \right)}}, $$
(12)
$$\begin{array}{l} f_{3} \left( {{\mathbf{x}};{\mathbf{b}}} \right) = {{\left\{ \begin{array}{l} Y_{v} \left( u \right)v + Y_{r} \left( u \right)r + Y_{vvv} \left( u \right)v^{3} + Y_{vvr} \left( u \right)v^{2} r + Y_{vrr} \left( u \right)vr^{2} + Y_{rrr} \left( u \right)r^{3} \hfill \\ + Y_{\varphi } \left( u \right)\varphi + Y_{R} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\zeta_{G} ,u,\varphi ,\theta ,\chi ,\delta ;n} \right) + Y_{W} \left( {\xi_{G} ,u,\chi ,t} \right) - \left( {m + m_{x} } \right)ur \hfill \\ \end{array} \right\}} \mathord{\left/ {\vphantom {{\left\{ \begin{aligned} Y_{v} \left( u \right)v + Y_{r} \left( u \right)r + Y_{vvv} \left( u \right)v^{3} + Y_{vvr} \left( u \right)v^{2} r + Y_{vrr} \left( u \right)vr^{2} + Y_{rrr} \left( u \right)r^{3} \hfill \\ + Y_{\varphi } \left( u \right)\varphi + Y_{R} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\zeta_{G} ,u,\varphi ,\theta ,\chi ,\delta ;n} \right) + Y_{W} \left( {\xi_{G} ,u,\chi ,t} \right) - \left( {m + m_{x} } \right)ur \hfill \\ \end{aligned} \right\}} {\left( {m + m_{y} } \right)}}} \right. \kern-0pt} {\left( {m + m_{y} } \right)}}, \end{array}$$
(13)
$$ f_{4} \left( {{\mathbf{x}};{\mathbf{b}}} \right) = r, $$
(14)
$$ f_{5} \left( {{\mathbf{x}};{\mathbf{b}}} \right) = {{\left\{ \begin{aligned} N_{v} \left( u \right)v + N_{r} \left( u \right)r + N_{vvv} \left( u \right)v^{3} + N_{vvr} \left( u \right)v^{2} r + N_{vrr} \left( u \right)vr^{2} + N_{rrr} \left( u \right)r^{3} \hfill \\ + N_{\varphi } \left( u \right)\varphi + N_{R} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\zeta_{G} ,u,\varphi ,\theta ,\chi ,\delta ;n} \right) + N_{W} \left( {\xi_{G} ,\chi ,u,t} \right) + N_{T} \hfill \\ \end{aligned} \right\}} \mathord{\left/ {\vphantom {{\left\{ \begin{aligned} N_{v} \left( u \right)v + N_{r} \left( u \right)r + N_{vvv} \left( u \right)v^{3} + N_{vvr} \left( u \right)v^{2} r + N_{vrr} \left( u \right)vr^{2} + N_{rrr} \left( u \right)r^{3} \hfill \\ + N_{\varphi } \left( u \right)\varphi + N_{R} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\zeta_{G} ,u,\varphi ,\theta ,\chi ,\delta ;n} \right) + N_{W} \left( {\xi_{G} ,\chi ,u,t} \right) \hfill \\ \end{aligned} \right\}} {\left( {I_{zz} + J_{zzz} } \right)}}} \right. \kern-0pt} {\left( {I_{zz} + J_{zz} } \right)}}, $$
(15)
$$ f_{6} \left( {{\mathbf{x}};{\mathbf{b}}} \right) = p, $$
(16)
$$ f_{7} \left( {{\mathbf{x}};{\mathbf{b}}} \right) = {{\left\{ \begin{aligned} K_{v} \left( u \right)v + K_{r} \left( u \right)r + K_{vvv} \left( u \right)v^{3} + K_{vvr} \left( u \right)v^{2} r + K_{vrr} \left( u \right)vr^{2} + K_{rrr} \left( u \right)r^{3} \hfill \\ + K_{\varphi } \left( u \right)\varphi + K_{R} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\zeta_{G} ,u,\varphi ,\theta ,\chi ,\delta ;n} \right) + K_{W} \left( {\xi_{G} ,\chi ,u,t} \right) \hfill \\ + K_{{\dot{\varphi }}} \left( {u,p} \right) - mgGZ\left( {\xi_{G} ,\varphi ,t} \right) - \left( {m + m_{x} } \right)ur - m_{y} \dot{v}z_{H} \hfill \\ \end{aligned} \right\}} \mathord{\left/ {\vphantom {{\left\{ \begin{aligned} K_{v} \left( u \right)v + K_{r} \left( u \right)r + K_{vvv} \left( u \right)v^{3} + K_{vvr} \left( u \right)v^{2} r + K_{vrr} \left( u \right)vr^{2} + K_{rrr} \left( u \right)r^{3} \hfill \\ + K_{\varphi } \left( u \right)\varphi + K_{R} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\zeta_{G} ,u,\varphi ,\theta ,\chi ,\delta ;n} \right) + K_{W} \left( {\xi_{G} ,\chi ,u,t} \right) \hfill \\ + K_{{\dot{\varphi }}} \left( {u,p} \right) - mgGZ\left( {\xi_{G} ,\varphi ,t} \right) - \left( {m + m_{x} } \right)ur - m_{y} \dot{v}z_{H} \hfill \\ \end{aligned} \right\}} {\left( {I_{xx} + J_{xx} } \right)}}} \right. \kern-0pt} {\left( {I_{xx} + J_{xx} } \right)}}, $$
(17)
$$ f_{8} \left( {{\mathbf{x}};{\mathbf{b}}} \right) = {{\left\{ { - \delta - K_{P} \left( {\chi - \chi_{C} } \right) - K_{P} T_{D} r} \right\}} \mathord{\left/ {\vphantom {{\left\{ { - \delta - K_{P} \left( {\chi - \chi_{C} } \right) - K_{P} T_{D} r} \right\}} {T_{E} }}} \right. \kern-0pt} {T_{E} }}. $$
(18)

The expression of each term in the state equation can be found in “Appendix”.

4.2 Validation of the calculation model of wave-induced force

Wave-induced force as the sum of the Froude–Krylov force and the hydrodynamic lift forces acting on the hull and the rudders due to wave particle velocity were modeled as follows: [43]

$$ X_{W} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },\chi } \right) = - \alpha \rho g\zeta_{a} k\cos \chi \int\limits_{AE}^{FE} {C_{1} \left( x \right)} S\left( x \right){\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} \sin k\left( {\xi_{G} + x\cos \chi } \right){\text{d}}x, $$
(19)
$$ \begin{aligned} Y_{W} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },u,\chi } \right) = \rho g\zeta_{a} k\;\sin \chi \int\limits_{AE}^{FE} {C_{1} \left( x \right)S\left( x \right){\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} \sin k\left( {\xi_{G} + x\;\cos \chi } \right)} {\text{d}}x \hfill \\ - \zeta_{a} \omega u\;\sin \chi \left[ {\rho S_{y} \left( x \right){\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} \cos k\left( {\xi_{G} + x\;\cos \chi } \right)} \right]_{AE}^{FE} , \hfill \\ \end{aligned} $$
(20)
$$ \begin{aligned} N_{W} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },u,\chi } \right) = \rho g\zeta_{a} k\;\sin \chi \int\limits_{AE}^{FE} {C_{1} \left( x \right)S\left( x \right){\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} x\;\sin k\left( {\xi_{G} + x\;\cos \chi } \right)} {\text{d}}x \hfill \\ + \zeta_{a} \omega u\;\sin \chi \int\limits_{AE}^{FE} {\rho S_{y} \left( x \right){\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} \cos k\left( {\xi_{G} + x\;\cos \chi } \right)} {\text{d}}x \hfill \\ - \zeta_{a} \omega u\;\sin \chi \left[ {\rho S_{y} \left( x \right){\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} x\;\cos k\left( {\xi_{G} + x\;\cos \chi } \right)} \right]_{AE}^{FE} , \hfill \\ \end{aligned} $$
(21)
$$ \begin{aligned} K_{W} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },u,\chi } \right) = \rho g\zeta_{a} k\;\sin \chi \int\limits_{AE}^{FE} {C_{1} \left( x \right)\frac{B\left( x \right)}{2}\left\{ {d\left( x \right)} \right\}^{2} {\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} \sin k\left( {\xi_{G} + x\;\cos \chi } \right)} dx \hfill \\ - \rho g\zeta_{a} k^{2} \sin \chi \int\limits_{AE}^{FE} {C_{4} \left( x \right)\left\{ {d\left( x \right)} \right\}^{3} {\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} \sin k\left( {\xi_{G} + x\;\cos \chi } \right)} dx \hfill \\ - \zeta_{a} \omega u\;\sin \chi \left[ {\rho S_{y} l_{n} \left( x \right){\text{e}}^{{ - {{kd\left( x \right)} \mathord{\left/ {\vphantom {{kd\left( x \right)} 2}} \right. \kern-0pt} 2}}} \cos k\left( {\xi_{G} + x\;\cos \chi } \right)} \right]_{AE}^{FE} \hfill \\ + Y_{w} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },u,\chi } \right) \cdot \overline{OG} , \hfill \\ \end{aligned} $$
(22)
$$ C_{1} = \frac{{\sin \left( {k\;\sin \chi \cdot {{B\left( x \right)} \mathord{\left/ {\vphantom {{B\left( x \right)} 2}} \right. \kern-0pt} 2}} \right)}}{{k\;\sin \chi \cdot {{B\left( x \right)} \mathord{\left/ {\vphantom {{B\left( x \right)} 2}} \right. \kern-0pt} 2}}}, $$
(23)
$$ C_{4} = \left\{ {k\;\sin \chi \cdot {{B\left( x \right)} \mathord{\left/ {\vphantom {{B\left( x \right)} 2}} \right. \kern-0pt} 2}} \right\}^{ - 3} \left[ {2\sin \left\{ {k\;\sin \chi \cdot {{B\left( x \right)} \mathord{\left/ {\vphantom {{B\left( x \right)} 2}} \right. \kern-0pt} 2}} \right\} - k\;\sin \chi \cdot B\left( x \right)\cos \left\{ {k\;\sin \chi \cdot {{B\left( x \right)} \mathord{\left/ {\vphantom {{B\left( x \right)} 2}} \right. \kern-0pt} 2}} \right\}} \right]. $$
(24)

The empirical correction factor for diffraction effect α (=0.92) was used only for surge [47].

For the validation of this model, a captive model test and calculation was conducted with the subject ship model in regular waves. Here, the model was free in heave and pitch. The wave-induced surge and sway forces and yaw and roll moments were measured with a dynamometer. The wave steepness was 0.025, the wavelength to ship length ratio was 1.25, the Froude number was 0.31, and the heading angle from wave direction, χ, was 30°. Obliquely towing the model without propellers was realized by combining an X–Y towing carriage with a turntable.

Here, wave-induced force was normalized as follows:

$$ X_{W}^{{\prime }} ,Y_{W}^{{\prime }} = {{X_{W} ,Y_{W} } \mathord{\left/ {\vphantom {{X_{W} ,Y_{W} } {\left( {\frac{HW}{\lambda }} \right)}}} \right. \kern-0pt} {\left( {\frac{HW}{\lambda }} \right)}}, $$
(25)
$$ N_{W}^{{\prime }} = {{N_{W} } \mathord{\left/ {\vphantom {{N_{W} } {\left( {\frac{HWL}{\lambda }} \right)}}} \right. \kern-0pt} {\left( {\frac{HWL}{\lambda }} \right)}}, $$
(26)
$$ K_{W}^{{\prime }} = {{K_{W} } \mathord{\left/ {\vphantom {{K_{W} } {\left( {\frac{HWB}{\lambda }} \right)}}} \right. \kern-0pt} {\left( {\frac{HWB}{\lambda }} \right)}}. $$
(27)

As Fig. 3 shows, the results of the calculation of wave-induced yaw moment do not agree with the experimental results. This discrepancy has been noted by many researchers [48, 49] and has been attributed to the linear slender body with or without free surfaces. The discrepancy between the slender body theory and the captive experiment that was found in the present study can be attributed to complicated vortex shedding. In the linear slender body theory, the wave-induced force on each section is integrated along the longitudinal axis. The vortex is assumed to be shed only at the aft end, although in reality this could be done at the separation point of the three-dimensional boundary layer on the hull surface. In the numerical calculation described here, the authors corrected the amplitude and the phase of wave-induced yaw moment, N W ′, to be fitted with the captive model experiment as shown in Fig. 4, i.e., \( N_{W}^{{\prime }} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda },u,\chi } \right) = 1.58N_{W0}^{{\prime }} \left( {{{\xi_{G} } \mathord{\left/ {\vphantom {{\xi_{G} } \lambda }} \right. \kern-0pt} \lambda } + 0.15,u,\chi } \right), \) where N W0′ means the value calculated by Eq. 21. In future work, the physical background to this empirical correction, for the same vessel, will be quantitatively analyzed using a CFD calculation.

Fig. 3
figure 3

Comparison of wave-induced surge and sway forces and yaw and roll moments for the ship in regular waves. Here, the wave steepness was 0.025, the wavelength to ship length ratio 1.25, the Froude number 0.31, and the heading angle from wave direction, χ, 30°

Full size image
Fig. 4
figure 4

Correction of the calculation results for wave-induced yaw moment

Full size image

5 Free-running model experiment

To validate the time-domain simulation in regular waves and the theoretical estimation method of broaching probability, free-running model experiments were carried out for the subject ship in a seakeeping and maneuvering basin of the National Research Institute of Fisheries Engineering. The experimental procedure for stern-quartering waves was based on the ITTC-recommended procedure for an intact stability model test [50]. First, the ship model was secured with a guide rope near a wave maker, which then began to generate waves. A radio operator used an onboard system to increase the propeller revolutions up to a specified level and to initiate automatic directional control. After the generated wave trains had propagated far enough, the guide rope was disconnected and the ship began running automatically in following and stern-quartering waves, while attempting to maintain the specified propeller rate and the autopilot course. Throughout this research, the specified propeller rate was given by the nominal Froude number, which is equivalent to the Froude number when the ship is running in otherwise calm water with that propeller rate.

The proportional autopilot was controlled by a computer and a fiber-optic gyro with a rudder gain of 3.0. The roll angle, pitch angle, yaw angle, rudder angle, and propeller rate were recorded by an onboard computer. The water surface elevation was measured with a servo-needle-type wave probe attached to the towing carriage of the basin near the wave maker.

The position of the center of ship gravity (ξ G , η G , ζ G ) on the space-fixed coordinate system was measured instantaneously with a total station system consisting of a theodolite and two prisms attached to the model (Fig. 5). The theodolite emitted light at 20 Hz and followed the prisms by measuring the phase of light reflected by the prisms. This allowed the estimation of the instantaneous position of the prisms, (ξ P , η P , ζ P ), on the space-fixed coordinate system. By combining this with roll angle, pitch angle, and yaw angle, the instantaneous position of the center of ship gravity could be obtained by Eqs. 6 and 7 [33].

Fig. 5
figure 5

Photograph of the ship model of ONR flare topside vessel during the experiment

Full size image

To generate long-crested irregular waves, the ITTC spectrum was specified and then the inverse Fourier transformation with random phases was used for the wave signals. Four hundred wave frequencies were sampled with non-equal increments. The incident wave spectrum estimated with the measured wave records and the fast Fourier transformation agreed closely with the specified spectrum, as shown in Fig. 6.

Fig. 6
figure 6

ITTC spectrum and the measured spectrum during experiments. Here, the significant wave height is 0.207 m and the zero-crossing mean wave period is 1.627 s. This wave was used for free-running model experiments described in Sect. 6.2

Full size image

6 Results and discussion

6.1 Evaluation of the time-domain numerical simulation for ships in regular waves

Figure 7 compares the time history of the free-running model experiment and the time-domain numerical simulation. The wave steepness was 0.06, the wavelength to ship length ratio was 1.25, the nominal Froude number was 0.43, the autopilot course was −15°, and the autopilot proportional gain was 3.0. In the experimental results, the ship started to yaw in the opposite direction to the maximum rudder angle, satisfying our definition of broaching. The numerical simulation results therefore reproduced the broaching phenomenon accurately. The maximum roll angle was around 40°. The time-domain simulation results modeled the free-running model experiment well at this stage. After the large roll due to broaching, the ship model was overtaken by the wave crest. At this stage, the numerical simulation failed to accurately reproduce the speed reduction, and the simulated ship was more slowly overtaken by the wave crest. Thus, some discrepancy in phase was found between the experiment and the simulation. However, in simple terms of the prediction of broaching, the numerical model performed adequately.

Fig. 7
figure 7

Comparison of the experiment and the simulation in time series for the ship in regular waves. Here, the wave steepness was 0.06, the wavelength to ship length ratio was 1.25, the nominal Froude number was 0.43, the autopilot course was −15°, and the autopilot proportional gain was 3.0

Full size image

We conducted several free-running model experiments in regular waves with a wavelength to ship length ratio of 1.25. Figure 8 compares the broaching region in the time-domain numerical simulations with the experimental results. The same criteria for broaching were applied, and the comparison was presented at full scale. The experimental results matched those obtained by simulation, both for broaching within the broaching region and non-broaching outside the broaching region or at its border. Thus, the time-domain simulation model was strongly validated.

Fig. 8
figure 8

Comparison of the experiment and simulation in broaching region for the ship in regular waves. Here, the wavelength to ship length ratio is 1.25

Full size image

6.2 Evaluation of the theoretical estimation of broaching probability when the ship meets an encounter wave in irregular waves

To test the theoretical estimation of broaching probability when the ship meets an encounter wave, free-running model experiments were conducted with irregular waves. The experimental procedure is shown in Sect. 5, but for irregular waves. In the free-running model experiments, the significant wave height was 0.207 m, the zero-crossing mean wave period was 1.627 s, the autopilot course was −15°, the autopilot proportional gain was 3.0, and the nominal Froude number was 0.44. In total, 50 realizations were conducted with different random wave phases. During the 50 realizations, the ship model encountered 104 waves and broaching occurred 9 times. Thus, the simple estimate of broaching probability when the ship meets an encounter wave was 0.0865. Since the occurrence of broaching is binomial, 95 % confidence interval of the theoretical broaching probability was obtained using the F distribution. An example of the time records of broaching measured in free-running model experiments in irregular waves is shown in Fig. 9 in model scale. While t is between 17.55 and 18.75 s, despite the maximum rudder deflection, yaw angular velocity develops in the opposite direction. Thus, we can regard it as broaching in irregular waves. Comparing it with broaching in regular waves such as in Fig. 7, the behavior leading to broaching is more complicated due to wave irregularity.

Fig. 9
figure 9

Example of time records of measured broaching in free-running model experiment in irregular waves

Full size image

Broaching probability was calculated theoretically as shown in Sect. 2. Figure 10 shows the regions of broaching associated with surf riding in regular waves. In the calculation, we first estimated the zone for surf riding using Melnikov analysis [23] and then executed the time-domain simulation for broaching within the surf riding zone. The obtained zone is represented by S in Eq. 1. Figure 11 compares the broaching probability obtained from the theoretical estimation based on Eq. 1 and that obtained from the experimental result. The theoretically calculated broaching probability was within the 95 % confidence interval of the simple estimate from the experimental findings.

Fig. 10
figure 10

Calculated broaching regions in regular waves of various wave steepness and wavelength. The nominal Froude number used here is 0.44. The black dot indicates a case of broaching

Full size image
Fig. 11
figure 11

Comparison of broaching probability between model experiments and numerical simulations for the ship in irregular waves. Here, the significant wave height was 0.207 m, the zero-crossing mean wave period 1.627 s, the autopilot course −15°, and the autopilot proportional gain 3.0

Full size image

6.3 Evaluation of broaching danger in actual seas

With this numerical simulation and the theoretical estimation, the broaching probability when the ship meets an encounter wave can be calculated as shown in Fig. 12. Table 1 gives the Beaufort scale and the relevant wave height and wave period applied. The relationship between the Beaufort number and the significant wave height, H 1/3, is specified by the World Meteorological Organization (WMO). The mean wave period, T 01, is calculated as follows:

$$ T_{01} = 3.86\sqrt {H_{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} } , $$
(28)

where \( \overline{c} \) and \( \overline{\lambda } \) are the wave celerity and the wavelength of the sinusoidal wave whose mean wave period is equal to T 01. They are calculated as follows:

$$ \overline{c} = \frac{{gT_{01} }}{2\pi }, $$
(29)
$$ \overline{\lambda } = \frac{{gT_{01}^{2} }}{2\pi }. $$
(30)
Fig. 12
figure 12

Broaching probability theoretically obtained for the ship in irregular waves as a function of the Beaufort scale with 0.44 and 0.31 of nominal Froude number

Full size image
Table 1 Relationships among Beaufort number, significant wave height, and representative wavelength
Full size table

At sea, and when the Beaufort number is smaller, the estimated broaching probability for a ship with a nominal Froude number of 0.44 is lower than that for the one with a nominal Froude number of 0.31. This is because the ship with a nominal Froude number of 0.44 moves much faster than the relevant waves, and the ship is not so easily surf ridden.

7 Conclusions

To validate a theoretical method proposed by one of the authors [37, 38], using a deterministic broaching region and stochastic wave theory, we conducted free-running model experiments of a typical twin-propeller and twin-rudder ship in irregular waves. The broaching probability calculated by the theoretical method was within the 95 % confidence interval. We conclude that the theoretical prediction method proposed by Umeda et al. [38] is also applicable to twin-propeller and twin-rudder ships.

An empirical correction needed to be made for the wave-induced yaw moment found in the captive model experiment. In future research, the physical basis for this empirical correction will be explored using CFD.