1 Introduction

Offshore wind is recently expected as one of the promising renewable energy sources which may secure domestic energy as well as mitigate greenhouse gas emission. From technical and economical viewpoints, the floating type of wind turbine is considered to be the most feasible in the offshore. Because the motion of floating offshore wind turbines (FOWT) is directly related to the efficiency of power generation, it is necessary to analyze and predict their motions in wind, waves, and currents. FOWT is widely studied experimentally and numerically and the comparison among numerical models is also being carried out these days. In most of the numerical models, the motion of FOWT is mainly caused by wind, waves, and moorings. However, motions induced by vortex are not considered in those models.

A floating body in a flow experiences periodic motion which is induced by vortex associated with the separation of boundary layer at the body surface and this motion is called vortex-induced motion (VIM). When VIM occurs to a floating structure such as a FOWT, its periodic motion may increase the possibility of the fatigue fracture of the mooring lines in its long lifetime.

Vortex-induced vibration (VIV) has the same generation mechanism as VIM and it can be seen at a linear structure such as a riser pipe. Lie [1] stated that VIV occurs to a long cylindrical structure with elasticity and increases drag and tension in axis. He also mentioned that VIM occurs to a platform on the sea surface and amplifies the motion of the platform and increases tension of mooring. Goncalves et al. [2] showed another definition. They call VIM as the new name for VIV of floating structure and the characteristic of VIM comes from its low aspect ratio (AR), which is the ratio of length and breadth of the body. In addition to these definitions, in this study, VIV and VIM are distinguished by the restoring force of oscillation. When the restoring force of the phenomenon comes from elasticity of the structure, it is considered as VIV. On the other hand, when the restoring force comes from mooring lines, it is considered as VIM. A structure with high AR usually has the elasticity and tends to cause VIV while a structure with low AR has little elasticity effect and tends to cause VIM. Therefore, this new definition of VIM is compatible with that of Goncalves et al. [2].

In this study, the wake of the floating body was divided into three regions. They are the free-surface region, the side-vortex region, and the end-cell region. A structure with high AR has small ratio of the free-surface and the end-cell regions. Therefore, their effects are less important than that of the side-vortex region. On the other hand, a structure with low AR has large ratio of the free-surface and the end-cell regions and the effects of these regions must be taken into consideration. In the side-vortex region, the well-known Kármán vortex can be seen and its pattern is dependent on Reynolds number (Re). Here Re is calculated by

$${Re} = \frac{DU}{\nu} ,$$
(1)

where D is the cylinder diameter, U is the flow velocity, and v is the kinematic viscosity. Kinematic viscosity was set as 1.0 × 10−6 m2/s, which is the value of the kinematic viscosity at 20 °C. In the free-surface region, it is known that vortex shedding is suspended and small size vortex is shed [3]. Goncalves et al. [4] found that the free surface and the end cell strengthen the 3-dimensionality of the flow around a floating body.

In addition, it is obvious that wave making resistance in the free-surface region increases drag coefficient and its influence is dependent on Froude number (Fr). Here Fr is calculated by

$${{Fr}} = \frac{U}{\sqrt {gD}} ,$$
(2)

where g is the gravity acceleration and it was set as 9.8 m/s2. In the end-cell region, some flow structures were classified by Kawamura et al. [5]. They are called recirculation, blowup and trailing vortex. These fluids phenomena in the end-cell region are illustrated in Fig. 1. The phenomenon called end-cell-induced vibration (ECIV) was discovered by Kitagawa et al. [6]. ECIV is the strong oscillation which occurs at one-third of flow velocity of VIV and it is caused by tip-associated vortex. This tip-associated vortex is also called as the trailing vortex by Sumner [7]. It is obvious that flow structures have effects on VIM but the dependency of free-surface effect, side-vortex effect, and end-cell effect on Re, Fr, and AR are not discussed comprehensively.

Fig. 1
figure 1

Flow structures around the end cell

Full size image

The aim of this study was the understanding of the effects of free-surface region, side-vortex region, and end-cell region to flow around a fixed circular cylinder with low AR and interpretation of its mechanism. To achieve this goal, two experiments were carried out. One is the particle image velocimetry (PIV) and the other is the hydrodynamic force measurement. The former was carried out to investigate flow structures around a fixed circular cylinder and the latter was carried out to analyze the effects of three regions quantitatively.

2 Flow measurement by PIV

2.1 Experimental setup

The PIV experiment was carried out at a circulating water channel, the observation section of which is 2 m in length, 0.3 m in breadth, and 0.3 m in height. Measured planes were set at the horizontal plane and the vertical plane, the latter of which was in-line to the flow across the center of the cylinder. The schematic diagram of experimental setups is shown in Fig. 2. Three cylinders were used and their diameters are 26, 38, and 60 mm, respectively, and their height was 160 mm in common. Flow velocity, U ranged from 0.1 to 0.26 m/s. Thus the Re ranged in this experiment from 4100 to 12600. The experimental cases are shown in Table 1.

Fig. 2
figure 2

Schematic diagram of PIV experiment setup for the measurement of the vertical cross section. The positions of the camera and light sheet are swapped for the measurement of the horizontal cross section

Full size image
Table 1 AR, Re, and Fr of PIV experiment
Full size table

In the PIV experiment, 2-dimensional velocity field in the target section was obtained by calculating the shift of particle groups between sequential camera images. A single camera was used in this study and the velocity vector perpendicular to the target section cannot be obtained in principle.

2.2 Results

The flow field was represented using flow vector and the vorticity vector. The vorticity vector was calculated by

$${\varvec{\upomega}} = \left( {\omega_{x} ,\omega_{y} ,\omega_{z} } \right) = \left( {\frac{\partial w}{\partial y} - \frac{\partial v}{\partial z},\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x},\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}} \right),$$
(3)

where vorticity vectors perpendicular to the vertical (X–Z) and the horizontal (X–Y) planes are represented by ω y and ω z , respectively. The period of vortex shedding, T e, is estimated by

$$T_{\text{e}} = \frac{D}{St\,U},$$
(4)

where St is the Strouhal number, which was approximated to be 0.2 for side vortexes.

Figure 3 shows sequential contours of the vertical component of instantaneous vorticity vector, ω z , around the cylinder for different measurement planes; one is located at the 1D above the free end of the body with AR = 4.0, and the other is at the free end of the body with AR = 3.0. It is found that vortex is generated from a cylinder and convected downstream in a–d. However, similar vortex convection in the downstream of the cylinder cannot be seen in a’–d’. This result indicates the disappearance of vortex with vertical axis at end-cell region. Figure 4 shows time-averaged streamwise velocity around a cylinder in horizontal planes at 1D above the end cell in (a) and at the end cell in (b). It is found that there is a region in which the flow speed is small behind a cylinder in (a), while there is no such a region in (b). This result indicates disappearance of low flow speed region: in other words, dead water region, at the end-cell region.

Fig. 3
figure 3

Sequential contours of the vertical component of instantaneous vorticity vector, ω z , around the circular cylinder at Re = 4100 in the horizontal plane. a–d are measured at 1D above the free end of the body with AR = 4.0, and a’–d’ are measured at the free end of the body with AR = 3.0

Full size image
Fig. 4
figure 4

Time-averaged streamwise velocity around a circular cylinder at Re = 4100 in the horizontal plane at 1D above the free end of the body with AR = 4.0 (a), and at the free end of the body with AR = 3.0 (b)

Full size image

Figure 5 shows time-averaged flow vector, streamwise and vertical velocity components around cylinders with different AR. From flow vector, forked flow can be observed. These graphs show blowup flow at the end cell and it separates into back flow and leeward flow. The blowup flow is observed in (b) and (e). The back flow is observed in (c) and (f). This back flow is equivalent to the recirculation. The deformation of flow from the end cell can be observed by comparing the results of AR = 2.0 and 1.0. The deformation is schematically illustrated in Fig. 6. The deformation may be because the free surface suspends the vertical flow. Figure 7 shows the minimum local velocity in the time-averaged back flow velocity field nondimensionalized by the inflow velocity, U, for various Fr. It is found that the maximum amplitude of back flow becomes small as Fr increases. This indicates that wave generation at the free surface may consume energy of recirculation and the strength of back flow becomes small. Figure 8 shows instantaneous vorticity around a cylinder in a vertical plane. It is found that there is vortex with horizontal axis around end cell. This vortex seems to be related to the recirculation. Moreover, this vortex is separated at a certain interval and the Strouhal number,

$$St = \frac{fD}{U},$$
(5)

where f is the vortex-shedding frequency calculated from the vertical interval of vortexes and the vertical time-averaged velocity, was approximately 0.06, which is close to St of trailing vortex shown in Kitagawa et al. [6]. From this result, it is deduced that the vortex associated with recirculation is separated periodically by the trailing vortex.

Fig. 5
figure 5

Flow around circular cylinders with different ARs at Re = 6400. AR = 2.0: a flow vector, b streamwise velocity, and c vertical velocity. AR = 1.0: d flow vector, e streamwise velocity, and f vertical velocity

Full size image
Fig. 6
figure 6

Conceptual images of deformation of end-cell flow caused by the free surface in steady state

Full size image
Fig. 7
figure 7

Effect of Fr on the strength of back flow for AR = 1 and AR = 2

Full size image
Fig. 8
figure 8

Vertical cross section of vorticity vector, ω y , around a circular cylinder with AR = 1.0 at Re = 9400

Full size image

3 Force measurement by towing experiment

3.1 Experimental setup and methods

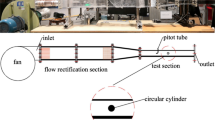
The hydrodynamic force measurement experiment was carried out in a towing tank, the test section of which is 85 m in length, 3.5 m in breadth, and 2.4 m in depth. Experimental settings are illustrated in Fig. 9. A semi-submerged cylinder was towed and the force was measured by a three-axis load cell. Three kinds of cylinders were used and their diameters are 0.2, 0.3, and 0.4 m, respectively. Table 2 shows conditions of three parameters, Re, Fr, and AR in the towing experiment. AR of underwater region, Re, and Fr ranged from 0.25 to 1.5, 28000 to 317000, 0.1 to 0.57, respectively. The measured time series of force was divided into mean and fluctuating components, the latter of which is calculated by the root-mean-square around mean. Moreover, frequency analysis was carried out to analyze the cause of oscillatory force.

Fig. 9
figure 9

Schematic diagram of the force measurement

Full size image
Table 2 AR, Re, and Fr of the hydrodynamic force measurement
Full size table

3.2 Results

Mean drag coefficient (C D), root-mean-squared drag coefficient (C Drms), and root-mean-squared lift coefficient (C Lrms) were obtained by cylinder towing experiment. The definitions of C D, C Drms, and C Lrms are

$$C_{\text{D}} = \frac{{\bar{F}_{x} }}{{\frac{AR}{2}\rho D^{2} U^{2} }}$$
(6)
$$C_{\text{Drms}} = \frac{{\left[ {\overline{{\left( {F_{x} - \bar{F}_{x} } \right)^{2} }} } \right]^{{\frac{1}{2}}} }}{{\frac{AR}{2}\rho D^{2} U^{2} }}$$
(7)
$$C_{\text{Lrms}} = \frac{{\left[ {\overline{{\left( {F_{y} - \bar{F}_{y} } \right)^{2} }} } \right]^{{\frac{1}{2}}} }}{{\frac{AR}{2}\rho D^{2} U^{2} }},$$
(8)

respectively, where overbar denotes temporal mean, ρ is the density of water, and F x , F y are the hydrodynamic forces in the streamwise and the cross-streamwise directions, respectively.

Figure 10 shows the effect of Re on C D, C Drms, and C Lrms for AR = 0.25 in (a) and 1.25 in (b). It is found that C Drms and C Lrms become small as Re increases in the both ARs. It is considered that this is because of the disordering of vortex as Re increases. It is found that C D becomes large as Re increases in (a), while C D becomes small as Re increases in (b). This indicates that the dependency of C D on Re changes by AR. The reason of this change will be considered later in the discussion. Figure 11 shows the effect of AR on C D, C Drms, and C Lrms at Re = 51300 and Fr = 0.1 in which the effect of free surface is considered to be small. It is found that C D becomes large and C Drms and C Lrms become small as AR increases. This indicates that for body with low AR, C D becomes small and C Drms and C Lrms become large by the effects of end cell and free surface. Because the effect of the trailing vortex becomes relatively small as AR increases, C Drms and C Lrms become small. Figure 12 shows the effect of Re on C D, C Drms, and C Lrms at higher Fr than Fig. 10. Although Fr is different in between Figs. 10 and 12, the same tendency is observed. C Drms and C Lrms become small as Re increases and the dependency of C D on Re changes between in (a) and (b). Figure 13 shows the effect of Fr on C D, C Drms, and C Lrms. It is found that C D becomes large and C Drms and C Lrms become small as Fr increases. This is considered to be because wave generation makes resistance and waves break the vortex near the free surface.

Fig. 10
figure 10

Effect of Re on C D, C Drms, and C Lrms at Fr = 0.1 with a AR = 0.25, and b AR = 1.25

Full size image
Fig. 11
figure 11

Effect of AR on CD, C Drms, and C Lrms at Re = 51300 and Fr = 0.1

Full size image
Fig. 12
figure 12

Effect of Re on C D, C Drms, and C Lrms at Fr = 0.4 with a AR = 0.25, and b AR = 1.25

Full size image
Fig. 13
figure 13

Effect of Fr on C D, C Drms, and C Lrms at Re = 160000 with a AR = 0.25, and b AR = 1.25

Full size image

Figure 14 shows frequency-based power spectra of lift coefficient. When AR = 0.25, the dominant fluctuation is at St = 0.02 and as AR increases, it is shifted to St = 0.15. Similar results were shown in Iungo et al. [8]. They analyzed the pressure fluctuation on the cylinder and indicated that lower frequency dominates fluctuation of pressure at end cell.

Fig. 14
figure 14

Frequency-based power spectra of lift coefficient at Re = 316800 with AR = 0.25 and AR = 1.25

Full size image

4 Discussion

4.1 Dependency of C Drms and C Lrms on Re, AR, and Fr

The dependency of C Drms and C Lrms on Re, AR, and Fr were shown in Tables  3, 4, 5. Frequency analysis of time series of hydrodynamic force showed that low-frequency component dominates phenomenon at low aspect ratio and this low-frequency component was considered to be caused by the trailing vortex. C Drms and C Lrms decrease as Re increases, which is considered to be caused by vortex disordering. C Drms and C Lrms decrease as AR increases, which is considered to be caused by relative decrease of the effect of the end-cell region, in which the trailing vortex is dominant. It is true that the free surface suspends the fluctuating component of forces as shown in Fig. 13 and it increases C Drms and C Lrms as AR increases. However, it is considered that its effect is less dominant compared with the end-cell effect. C Drms and C Lrms decrease as Fr increases, which is considered to be caused by waves which break vortex near the free surface.

Table 3 Dependency of C D, C Drms, and C Lrms on Re
Full size table
Table 4 Dependency of C D, C Drms, and C Lrms on Fr
Full size table
Table 5 Dependency of C D, C Drms, and C Lrms on AR
Full size table

4.2 Dependency of C D on Re, AR, and Fr

PIV results indicate that recirculation from the end cell induces back flow which pushes back the cylinder and it causes decrease of C D. As shown in Fig. 11, C D increases as AR increases, which is considered to be caused by the relative decrease of the effect of recirculation. As shown in Fig. 13, C D increases as Fr increases and this is simply considered to be caused by wave generation resistance.

4.3 Explanation for the variety of dependency of C D on Re

It was found that dependency of C D on Re varies with different ARs. A hypothesis is proposed in the following to explain the reason of this phenomenon.

Flow around a cylinder with low AR is likely to become 3-dimensional because of the end-cell effect. It is deduced that the flow with vertical variation disturbs the boundary layer near the cylinder surface and consequently causes separation of boundary layer even when Re is smaller than its critical value. This causes reduction of C D with increasing Re when the effect of end cell is less dominant. On the other hand, the structure of recirculation is considered to become complicated with increasing Re and this may cause reduction of pressure recovery from recirculation in dimensionless quantity. Therefore, C D becomes large with increasing Re when the effect of the end cell is dominant. With these two reasons, C D becomes large with increasing Re in low AR case in which the end-cell effect is dominant and C D becomes small with increasing Re in higher AR case in which the end-cell effect is less dominant.

To prove this hypothesis, understanding of pressure distribution in the wake of the cylinder is necessary. Some experimental approaches or computational simulations will be effective for this purpose.

5 Conclusion

The dependency of C D, C Drms, and C Lrms on Re, Fr, and AR and their mechanisms were investigated using flow measurement by PIV and force measurement. The effect of Re, Fr, and AR on drag and lift coefficients are analyzed comprehensively. It was shown that AR is strongly related to the effects of free surface and end cell; their effects become large for low AR. It was newly found that the dependency of C D on Re is different for different ARs. A possible explanation to this was proposed and its verification requires further investigation.

The result of this study was restricted to a fixed cylinder. The expansion to a moored cylinder is necessary to analyze the effect of end cell and free surface on VIM. This is left to our future work.