Skip to main content
SpringerLink
Log in

Prediction of the forces acting on container carriers in muddy navigation areas using a fluidization parameter

  • Original Article
  • Published:
Journal of Marine Science and Technology Aims and scope Submit manuscript

Abstract

To assess the safety of navigation in muddy areas, a comprehensive captive manoeuvring model test program was executed. Based on the results of this experimental program, a four-quadrant manoeuvring model was built with a separate set of coefficients for each combination of under-keel clearance and mud layer characteristics. The disadvantage of this model is that only conditions corresponding with the experimental ones can be simulated. A more consolidated mathematical model was needed. This was achieved with the introduction of a fluidization parameter that determines the corresponding hydrodynamically equivalent depth above a solid bottom. As a result, the under-keel clearance dependency of a given mathematical manoeuvring model can be reformulated in such way that the effect of any realistic muddy condition is included. In this article, the modelling of the hull forces, the propeller thrust and torque, and the forces acting on the rudder will be discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30

Similar content being viewed by others

Abbreviations

a i :

Regression coefficient (–)

AEP:

Expanded area ratio of propeller (–)

A R :

Rudder area (m2)

B :

Ship beam (m)

C B :

Block coefficient (–)

C D :

Drag coefficient (–)

C L :

Lift coefficient (–)

C T(Q) :

Thrust (torque) coefficient (–)

D P :

Propeller diameter (m)

F :

Force component (–)

F X :

Longitudinal rudder force (N)

F Y :

Lateral rudder force (N)

f :

Function (–)

g :

Function (–)

g :

Gravity constant (m/s2)

G*:

Function (–)

h :

Depth/thickness (m)

h*:

Hydrodynamically equivalent depth (m)

I zz :

Moment of inertia about z-axis (kg m2)

J :

Advance (–)

J′:

Apparent advance (–)

K T(Q) :

Thrust (torque) coefficient (–)

k :

Sway velocity or yaw rate (m/s or rad/s)

L, L PP :

Ship length (m)

m :

Ship mass (kg)

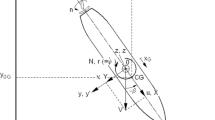
N :

Yawing moment (Nm)

n :

Propeller rate (1/s)

N i :

Hydrodynamic derivative \( \left({{i}} = \dot{\text{v}}, \; \dot{\text{r}}, \; \ldots \right) \)

N′(β):

Non-dimensional yawing moment due to drift: \( N^{\prime}\left( \beta \right) = \frac{N\left( \beta \right)}{{\frac{1}{2}\rho L^{2} T\left( {u^{2} + v^{2} } \right)}}\left( {\text{--}} \right) \)

N′(γ):

Non-dimensional yawing moment due to yaw: \( N^{\prime}\left( \gamma \right) = \frac{N\left( \gamma \right)}{{\frac{1}{2}\rho L^{2} T\left( {u^{2} + \left( {\tfrac{1}{2}rL} \right)^{ 2} } \right)}}\left({\text{--}}\right) \)

N′(χ):

Non-dimensional yawing moment due to yaw–drift correlation: \( N^{\prime}\left( \chi \right) = \frac{N\left( \chi \right)}{{\frac{1}{2}\rho L^{2} T\left( {v^{2} + \left( {\tfrac{1}{2}rL} \right)^{2} } \right)}}\left({\text{--}}\right) \)

P :

Ship’s length or draught (m)

P :

Propeller pitch (m)

Q P :

Propeller torque (Nm)

r :

Yaw rate (rad/s)

\( \dot{r} \) :

Yaw acceleration (rad/s2)

sgn:

Sign function (–)

T :

Ship draught (m)

T P :

Propeller thrust (N)

TEU:

Twenty feet equivalent unit (–)

u :

Longitudinal velocity (m/s)

u P :

Longitudinal velocity at propeller (m/s)

\( \dot{{u}} \) :

Longitudinal acceleration (m/s2)

UKC:

Under keel clearance

v :

Lateral velocity (m/s)

V R :

Velocity near rudder (m/s)

\( \dot{\text{v}} \) :

Lateral acceleration (m/s2)

w :

Wake factor (–)

X :

Longitudinal force (N)

X i :

Hydrodynamic derivative \( \left({{{i}} = \dot{{u}},\; \ldots} \right) \)

X′(β):

Non-dimensional longitudinal force due to drift: \( X^{\prime}\left( \beta \right) = \frac{X\left( \beta \right)}{{\frac{1}{2}\rho LT\left( {u^{2} + v^{2} } \right)}}\left( {\text{--}} \right) \)

X′(γ):

Non-dimensional longitudinal force due to yaw: \( X^{\prime}\left( \gamma \right) = \frac{X\left( \gamma \right)}{{\frac{1}{2}\rho LT\left( {u^{2} + \left( {\tfrac{1}{2}rL} \right)^{2} } \right)}}\left( {\text{--}} \right) \)

X′(χ):

Non-dimensional longitudinal force due to yaw–drift correlation: \( X^{\prime}\left( \chi \right) = \frac{X\left( \chi \right)}{{\frac{1}{2}\rho LT\left( {v^{2} + \left( {\tfrac{1}{2}rL} \right)^{2} } \right)}}\left( {\text{--}} \right) \)

x G :

Longitudinal position of centre of gravity (m)

Y :

Sway force (N)

Y i :

Hydrodynamic derivative \( \left({{\text{i}} = \dot{\text{v}},\;\dot{\text{r}},\ldots} \right) \)

Y′(β):

Non-dimensional lateral force due to drift: \( Y^{\prime}\left( \beta \right) = \frac{Y\left( \beta \right)}{{\frac{1}{2}\rho LT\left( {u^{2} + v^{2} } \right)}}\left( {\text{--}} \right) \)

Y′(γ):

Non-dimensional lateral force due to yaw: \( Y^{\prime}\left( \gamma \right) = \frac{Y\left( \gamma \right)}{{\frac{1}{2}\rho LT\left( {u^{2} + \left( {\tfrac{1}{2}rL} \right)^{2} } \right)}}\left( {\text{--}} \right) \)

Y′(χ):

Non-dimensional lateral force due to yaw–drift correlation: \( Y^{\prime}\left( \chi \right) = \frac{Y\left( \chi \right)}{{\frac{1}{2}\rho LT\left( {v^{2} + \left( {\tfrac{1}{2}rL} \right)^{2} } \right)}}\left( {\text{--}} \right) \)

α:

Angle of attack of flow (°)

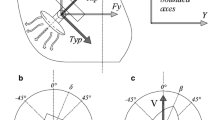
β:

Drift angle, Eq. 14 (°)

γ:

Yaw rate angle, Eq. 15 (°)

δ:

Rudder angle (°)

ε:

Hydrodynamic angle, Eq. 42 (°)

ε*:

Apparent hydrodynamic angle, Eq. 50 (°)

μ :

Dynamic viscosity (Pa s)

μ′:

Non-dimensional dynamic viscosity: μ′ = μ/(1 Pa s) (–)

\(\Uppi\) T :

Keel penetration parameter, Eq. 17 (–)

\(\Uppi\) :

Alternative keel penetration parameter, Eq. 20 (–)

ξ i :

Regression coefficient or function (–)

ρ:

Density (kg/m3)

ρ*:

Non-dimensional density, Eq. 47 (–)

Φ:

Fluidization parameter (–)

Φ ij :

Regression coefficient (–)

χ:

Drift–yaw correlation angle, Eq. 16 (°)

1:

Water layer

2:

Mud layer

H:

Hull

P:

Propeller

Q:

Torque

R:

Rudder

T:

Thrust

References

  1. PIANC (1997) Approach channels––a guide for design. Final report of the joint working group PIANC and IAPH, in cooperation with IMPA and IALA. Supplement to bulletin no. 95, PIANC, Brussels

  2. De Vlieger H (1991) Economic methods of channel maintenance: optimization of maintenance dredging. Terra et Aqua 45:32–51

    Google Scholar 

  3. Kerckaert P, Malherbe B, Bastin A (1985) Navigation in muddy areas––the Zeebrugge experience. Bulletin 48, PIANC, Brussels, pp 127–135

  4. Malherbe B (1990) Towards a definition of the nautical bed in mud deposits: the concept of rheologic transition RT. In: International workshop on cohesive sediments: towards a definition of “mud”. KBIN, Brussels

  5. Brossard C, Delouis A, Galichon P et al (1990) Navigability in channels subject to siltation. In: Proceedings of the 22nd international coastal engineering conference. American Society of Civil Engineers, Reston, pp 3088–3101

  6. Sellmeijer R, Van Oortmerssen G (1983) The effect of mud on tanker manoeuvres. In: Spring meetings, paper no. 7, The Royal Institution of Naval Architects, London

  7. Vantorre M, Coen I (1988) On sinkage and trim of vessels navigating above a mud layer. In: Harbour congress, The Royal Society of Flemish Engineers, Antwerp

  8. Doctors LJ, Zilman G, Miloh T (1996) The influence of a bottom mud layer on the steady-state hydrodynamics of marine vehicles. In: 21st symposium on naval hydrodynamics. National Academies Press, Washington, pp 727–742

    Google Scholar 

  9. Miloh T (1995) Ship motion in non-homogeneous media. Ship Technol Res 42(3):140–156

    MathSciNet  Google Scholar 

  10. Miloh T, Tulin MP, Zilman G (1992) Dead water effects of a ship moving in stratified seas. Trans Am Soc Mech Eng J Offshore Mech Arctic Eng 115:105–110

    Google Scholar 

  11. Wu GX (1993) The representation of a body advancing in a stratified fluid by singularity distribution. Int Shipbuild Prog 40(422):127–135

    Google Scholar 

  12. Zilman G, Miloh T (1995) Hydrodynamics of a body moving over a mud layer––part 1: wave resistance. J Ship Res 39(3):194–201

    Google Scholar 

  13. Zilman G, Kagan L, Miloh T (1996) Hydrodynamics of a body moving over a mud layer––part 2: added mass and damping coefficients. J Ship Res 40(1):39–45

    Google Scholar 

  14. Zilman G, Miloh T (1996) Hydrodynamics of a body moving over a mud layer. In: Proceedings of the 20th symposium on naval hydrodynamics. National Academy Press, Washington, 18 pp

  15. Stern F, Bulgarelli U, Gustafsson L et al (1999) Uncertainty analysis in EFD: uncertainty assessment methodology. ITTC quality manual, 4.9-03-01-01

  16. Delefortrie G, Vantorre M, Eloot K (2005) Modelling navigation in muddy areas through captive model tests. J Marine Sci Technol 10(4):188–202

    Article  Google Scholar 

  17. Ogawa A, Kasai H (1978) On the mathematical model of manoeuvring motion of ships. Int Shipbuild Prog 25(292):306–319

    Google Scholar 

  18. Oltmann P, Sharma SD (1984) Simulation of combined engine and rudder maneuvers using an improved model of hull-propeller-rudder interactions. 15th symposium on naval hydrodynamics. National Academies Press, Washington, pp 83–108

    Google Scholar 

  19. Delefortrie G, Vantorre M, Verzhbitskaya E, Seynaeve K (2007) Evaluation of safety of navigation in muddy areas through real-time manoeuvring simulation. J Waterw Port Coast Ocean Eng 133:125–135

    Article  Google Scholar 

  20. Gronarz A (1993) A mathematical model for manoeuvring simulation on shallow water. In: Proceedings of the international conference on marine simulation and ship manoeuvrability (MARSIM), Saint John’s

  21. Kijima K, Nakiri Y, Tsutsui Y, Matunaga M (1990) Prediction method of ship manoeuvrability in deep and shallow waters. In: Proceedings of MARSIM and ICSM 90, Tokyo, pp 311–318

  22. Li M, Wu X (1990) Simulation calculation and comprehensive assessment on ship maneuverabilities in wind, wave, current and shallow water. In: Proceedings of MARSIM and ICSM ‘90, Tokyo, pp 403–411, 459–465

  23. Delefortrie G, Vantorre M (2007) Modeling the maneuvering behavior of container carriers in shallow water. J Ship Res 51(4):287–296

    Google Scholar 

Download references

Acknowledgments

The generalised mathematical model is based on experimental results obtained at and in close co-operation with Flanders Hydraulics Research (Antwerp, Belgium) and has been developed in the framework of the research project Validation of the Nautical Bottom Concept by order of the Flemish Government (ref 16 EB/0501), Belgium.

Author information

Authors and Affiliations

  1. Flanders Hydraulics Research, Berchemlei 115, 2140, Antwerp, Belgium

    Guillaume Delefortrie

  2. Maritime Technology Division, Ghent University, Technologiepark 904, 9052, Ghent, Belgium

    Marc Vantorre

Authors
  1. Guillaume Delefortrie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marc Vantorre
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guillaume Delefortrie.

Appendix: Influence of sway and yaw acceleration on the longitudinal force

Appendix: Influence of sway and yaw acceleration on the longitudinal force

Here, the reason for extending the model of the longitudinal force to encompass the influence of sway and yaw acceleration is explained. The yaw acceleration is taken as an example. Consider Fig. 31: when building a model for X′(β) + X′(γ) with a constant drift angle, e.g. 0°, and small yaw angles, the data can normally be modelled using a parabolic expression G* as a function of the yaw angle. However, when navigating in contact with highly viscous mud layers, some measurements have shown a large deviation from the proposed model G*. These deviations are presented in Fig. 32 as a function of the yaw acceleration. It seems that a counteracting force effect occurs that depends on the square of the yaw acceleration.

Fig. 31
figure 31

Measured drift–yaw function for the longitudinal force versus the modelled values for mud g2 and a UKC of −1.1%

Full size image
Fig. 32
figure 32

Model rest fraction as a function of the yaw acceleration for mud g2 and a UKC of −1.1%

Full size image

The deviations are probably related to the behaviour of the mud–water interface. It is very clear that it would be more appropriate to represent these effects by non-stationary terms, but this was not possible within the scope of the project. Moreover, the sway and yaw acceleration-dependent terms appear to have only a small effect compared to the other terms.

About this article

Cite this article

Delefortrie, G., Vantorre, M. Prediction of the forces acting on container carriers in muddy navigation areas using a fluidization parameter. J Mar Sci Technol 14, 51–68 (2009). https://doi.org/10.1007/s00773-009-0041-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00773-009-0041-x

Keywords

Search

Navigation