Abstract
The magnetic anisotropy of the quantum-critical spin-chain system YbAlO\(_3\) is studied in detail in its paramagnetic phase by means of electron spin resonance. We find an uniaxial g factor anisotropy with \(g_\parallel =7.01\) and \(g_\perp = 0.47\). The existence of two distinct magnetic Yb sites explains the resonance spectra well.
Similar content being viewed by others
1 Introduction
Among the reasons for the continuous interest in rare-earth compounds in solid state physics, there is a wide range of particular magnetic properties: large magnetic moments, orbital moment magnetism, strong spin–orbit coupling, and a variety of magnetic couplings either between rare-earth ions or to transition metal ions. Consequently, in well-known structural families like the perovskites, the introduction of rare-earth elements to systems which have otherwise been considered in view of transition metal magnetism has led to a large enrichment in the knowledge of magnetic phenomena [1,2,3]. In this work, we focus on the magnetic anisotropy of the perovskite YbAlO\(_3\), partly because the precise determination of its strong g factor anisotropy has proven experimentally challenging [4, 5], but also because this compound is in the focus of recent research due to its interesting low-temperature properties [6, 7]. The crystal structure is that of an orthorhombicly distorted perovskite [8, 9] and magnetic order is observed below the Néel-temperature \(T_\mathrm N = 0.88~\mathrm K\). It is in this low-temperature region that a quantum spin \(S = \frac{1}{2}\) chain is formed, giving rise to Tomonaga–Luttinger liquid behaviour, quantum criticality, and spinon physics [6]. Even more recently, the coherent multiple scattering of fermionic quasiparticles has proven the possibility of a band structure control of emergent physics [7].
The magnetic anisotropy is well visible in magnetisation measurements, which have shown the saturation moments to be more than an order of magnitude larger in the ab plane than along the c direction [10]. More precisely, the Yb\(^{3+}\) ions have strong uniaxial anisotropy, where the c direction is within the hard plane and the easy axis is lying in the ab plane. However, due to the crystallographic surrounding of the Yb\(^{3+}\), the easy axis is not unique. As pointed out in Ref. [10], there are two easy axes in the ab plane spanning angles of \(\pm 23.5^\circ\) with the a direction, thus belonging to two different Yb sites.
In this study, the g factor anisotropy of Yb\(^{3+}\) shall be studied in the paramagnetic region. Electron spin resonance (ESR) is chosen to access the anisotropic behaviour because of its strong sensitivity to the g factor.
2 Methods
Continuous-wave ESR was performed with a Bruker Elexsys spectrometer at a frequency of \(\nu _\mathrm {rf} = 34~\mathrm {GHz}\) (Q-band). As an electromagnetic resonator, a cylindrical Bruker ER5106QTW cavity was used. It is placed within a helium gas-flow cryostat, which allows a temperature stability of less than 0.1 K at temperatures \(T < 20~\mathrm {K}\). The external field H was swept up to 18 kOe. The use of a lock-in technique with field modulation reduces noise in the spectra.
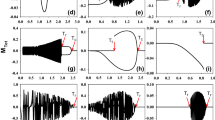
The single crystal of YbAlO\(_3\) used in this work has been grown by the Czochralski method; for details, see Ref. [11]. The sample was cut parallel to the ab and ac planes and Laue experiments confirmed the orientation of the ab plane. Therefore, it was possible to glue the sample on the front side of a glass stick, such that the c axis could be taken as the axis of rotation in our ESR experiments. The two photographs in Fig. 1 depict this geometric configuration. The face of the sample which is equal to the crystallographic ac plane is the second plane of rotation for this work (not shown in Fig. 1). With the aid of a goniometer (angular accuracy less than 2\(^\circ\)), the glass stick with the sample on its top could be rotated inside the resonator.
ESR spectra for three different angles of the field within the ab plane. In each case, a linear or, if required, a quadratic background has been subtracted from the raw spectra. The angle \(\varphi\) denotes the angle between the magnetic field and the a axis. \(\varphi\) values correspond to those in Fig. 2. The two photographs display a topview and a sideview of the sample glued to the top of the sample holder
3 Results and Discussion
The temperature evolution of the resonance field \(H_\mathrm {res}\) for \(H \parallel a\) has been measured and its decrease for decreasing temperatures (not shown) is well consistent with increasing demagnetisation fields on approaching \(T_\mathrm N\). In this work, we show the results for a temperature of \(T = 20~\mathrm K\), as this is a good compromise between low demagnetisation effects at higher temperatures and strong ESR signals at low temperatures.
As the crystallographic ab plane of YbAlO\(_3\) is expected to contain the magnetic easy axes as well as the corresponding hard planes [10], rotations of the magnetic field in this plane shall be the main focus of this ESR study. Figure 1 shows three selected spectra at the temperature \(T = 20~\mathrm K\) and at the field angles \(\varphi = -80^\circ , -25^\circ , +50^\circ\), where \(\varphi\) measures the angle between the field and the a axis [\(H \parallel a\) (\(\varphi = 0^\circ\)), \(H \parallel b\) (\(\varphi = 90^\circ\))]. The spectra are the first derivatives of the absorbed microwave power. In the figure, a linear or, if required, a quadratic background has been subtracted from the recorded spectra. Such background contributions to the signal stem from microphony induced by the field modulation coils. Linear backgrounds are typical, but Q-band data sometimes require a quadratic term. Figure 1 demonstrates that in general, the spectra exhibit two resonances. At \(\varphi = -25^\circ\), they are close to overlapping. A pronounced anisotropy of the resonance fields is obvious. Linewidths tend to become broader at higher fields and amplitudes of the resonances may differ between the angular-dependent spectra.
The spectra of this rotation have been fitted with one or two Lorentzian derivative lines. In combination with the mentioned background signal, the fits reproduce the spectra very well. Figure 2a shows the obtained resonance fields. Two curves can clearly be distinguished, here named “line 1” and “line 2”. The latter one has its minimum at \(\varphi \approx -23^\circ\) with the resonance field \(H_\mathrm {res} = 3470~\mathrm {Oe}\) and it leaves the accessible field range at \(\varphi \approx +56^\circ\). The resonance reappears at an angle of \(\varphi = 95^\circ\). Line 1 follows the same behaviour, but is horizontally shifted with respect to line 2, having its minimum at \(\varphi \approx +23^\circ\).
ESR parameters for field rotation in the ab plane at \(T = 20~\mathrm K\). a Angular dependence of resonance fields. Dots represent the measured data. Solid lines are the fits of uniaxial anisotropy to the data; see the main text. b The corresponding linewidths of the two resonances. c The intensity of resonance line 2 relative to the intensity of line 1. d The spin–spin relaxation rate for line 1
The green solid line in Fig. 2a is a fit to the resonance line 1 in terms of an uniaxial g tensor
Here, \(H_\mathrm {res}^\parallel\) and \(H_\mathrm {res}^\perp\) correspond to resonance fields parallel and perpendicular to the axis of anisotropy, respectively. \(\varphi '\) is the “uncalibrated” angle read from the goniometer. The angle \(\delta\) denotes an offset in the angle of the axis of anisotropy with respect to the origin of the graph. The resulting fit parameters are \(H_\mathrm {res}^\parallel = (3466 \pm 8)~\mathrm {Oe}\), \(H_\mathrm {res}^\perp = (51 \pm 4)~\mathrm {kOe}\) and \(\delta = 125.0^\circ \pm 0.1^\circ\). Using the microwave frequency of \(34~\mathrm {GHz}\), the corresponding components of the g tensor are calculated to \(g_\parallel =7.01 \pm 0.02\) and \(g_\perp = 0.47 \pm 0.04\). Despite \(H_\mathrm {res}^\perp\) being far outside the measured range, this fit converged well and the relative error of this parameter is acceptable. For line 2, however, it turned out to be not possible to achieve a reasonable convergence of the fit. Instead of leaving all three parameters free, we therefore fixed \(H_\mathrm {res}^\parallel\) and \(H_\mathrm {res}^\perp\) to the values obtained from line 1, thus leaving \(\delta\) as the only remaining free parameter. The resulting fit is seen as the pink solid line and we get \(\delta = 78.4^\circ \pm 0.5^\circ\). Half of the difference in the two \(\delta\) is \(23.3^\circ \pm 0.5^\circ\) in excellent agreement with the value between the crystallographic a axis and the easy directions as reported from neutron scattering and magnetisation measurements [10]. From the two \(\delta\), we deduce that H is parallel to a at \(\varphi ' = 101.7^\circ\) and \(\varphi\) is defined by shifting this angle to the origin (see Fig. 2).
For the ESR signals of two magnetic sites to be exchange-narrowed into a single line, the condition \(J > \vert g' - g''\vert \mu _\mathrm B H / 2\) must be fulfilled [12], where J is the exchange constant, \(g'\) and \(g''\) are the two g factors, and \(\mu _\mathrm B\) is Bohr’s magneton. This means the closer the two lines get to each other, the more likely they will be exchange-narrowed. Using \(J_c = J (H \parallel c) = 0.21~\mathrm {meV}\) [6], \(J_{ab} = 0.04 J_c\) [5] and \(H = 3800~\mathrm {Oe}\), the condition for exchange-narrowing in the angular region close to \(H \parallel a\) is \(\vert g' - g''\vert < 1.0\). This is equivalent to a difference in resonance fields of up to about 700 Oe or, according to Fig. 2a, to a restriction for the field direction of \(\vert \varphi \vert < \pm 12^\circ\). Indeed, the two lines can only be separated for \(\vert \varphi \vert > 8^\circ\), but this is also the case due to the fact that the lines are broader than their field separation close to \(H \parallel a\). The spin–spin relaxation rate \(\Gamma\) is calculated from the values of \(H_\mathrm {res}\) and the line width \(\Delta H\) (Fig. 2b) as \(\Gamma = \Delta H \times 2 \pi \nu _\mathrm {rf} / H_\mathrm {res}\). As shown in Fig. 2d, we get a value \(\Gamma = 4 \times 10^{10}~\mathrm s^{-1}\) which is basically independent of the field angle \(\varphi\) except for some scattering close to the angle where \(H_\mathrm {res}\) becomes very large. A detailed theoretical treatment of the linewidth in terms of dipolar broadening is generally considered difficult for such anisotropic ions like Yb\(^{3+}\) [12].
Figure 1 indicates that the intensities of the ESR lines vary a lot upon field rotation. Line intensities in Q-band experiments should generally be taken with care due to effects of change of the cavity quality factor upon changes in the sample position and orientation. A strong anisotropy of the intensity ratio of two lines (see Fig. 2c) within the same spectrum, however, suggests a physical origin. Thus, the observed strong angle dependence of the intensity indeed seems true. We found for line 2 that as \(\varphi\) increases from the direction of minimal \(H_\mathrm {res}\), the intensity continuously increases until the line gets out of our field range. When line 2 returns into the experimental field range, it is very weak at first, but recovers intensity on approaching the minimal \(H_\mathrm {res}\). Thus, it seems that as the field passes the experimentally not accessible hard direction with increasing \(\varphi\), the line intensity has a discontinuous jump towards low values. The same observation holds for line 1. For both lines, with decreasing \(\varphi\), i.e., on reverting the sense of field rotation, we find a discontinuous increase at the hard directions. Thus, this effect is entirely reversible. Figure 2c documents this behaviour in terms of the intensity ratio of the two lines. We did not find a satisfactory explanation of this phenomenon, but the idea of different spin configurations being stable under different field angles [10] in the ordered state suggests a relationship to our observation of discontinuities in ESR spectra. It is interesting to note that at \(H \parallel a\) (\(\varphi = 0^\circ\)) and at \(H \parallel b\) (\(\varphi = 90^\circ\)) in Fig. 2c, the intensity ratio is one in accordance with the symmetry consideration that both spin sites are equivalent in these cases.
When rotating the field in the ac plane, the two sites are undistinguishable and a single ESR line occurs. Figure 3 displays the resonance field at \(T = 20~\mathrm K\), where \(\theta\) is the angle between the field and the c axis. The a axis shows up as a broad minimum (\(\theta = 90^\circ\)), whereas \(H_\mathrm {res}\) increases towards the c axis (\(\theta = 0^\circ\) resp. \(\theta = 180^\circ\)). While the c axis is a hard direction, the a axis is only close to the easy direction, which is by 23.5\(^\circ\) away from the a axis in the ab plane. We tried to fit a uniaxial g tensor according to Eq. 1 to the data, where the angle argument is recalculated in the new plane, but did not obtain reasonable parameters due to the limited experimental data. Instead, we applied the fit parameters given above from the ab plane to the geometry of a field in the ac plane. This is shown as the solid line in Fig. 3. The huge maxima towards the hard direction demonstrate that a conventional ESR cannot capture the ac plane anisotropy sufficiently.
4 Conclusions
The idea of a strong uniaxial anisotropy with two magnetic sites that can be distinguished by their easy direction has previously been suggested only by macroscopic magnetisation measurements together with crystalline electric field calculations. We have demonstrated that this is clearly supported by ESR where we were able to get separate signals from the two Yb\(^{3+}\) sites. The angle of \(\pm 23.5^\circ\) between easy axes and a directions could be confirmed. Within the ab plane which contains the easy axes, the spin–spin relaxation shows an isotropic behaviour. Near the magnetic hard direction, we found an anomalous discontinuous behaviour of the line intensity pointing to a spin configuration stability being very sensitive to the field orientation. The obtained g tensor values are in remarkably good agreement with values reported in the literature [10] despite the maximal resonance field being far beyond our experimentally reachable limits. In this respect, these results demonstrate that rather precise magnetic parameters can still be obtained by ESR even in the case of very anisotropic systems.
References
E. Bousquet, A. Cano, J. Phys.: Condens. Mat. 28, 123001 (2016)
S.-W. Cheong, M. Mostovoy, Nat. Mat. 6, 13 (2007)
C. Moure, O. Peña, J. Magn. Mag. Mat. 337–338, 1 (2013)
P. Bonville, J.A. Hodges, P. Imbert, F. Hartmann-Boutron, Phys. Rev. B 18, 2196 (1978)
P. Radhakrishna, J. Hammann, M. Ocio, P. Pari, Y. Allain, Solid State Commun. 37(10), 813 (1981)
L.S. Wu, S.E. Nikitin, Z. Wang, W. Zhu, C.D. Batista, A.M. Tsvelik, A.M. Samarakoon, D.A. Tennant, M. Brando, L. Vasylechko, M. Frontzek, A.T. Savici, G. Sala, G. Ehlers, A.D. Christianson, M.D. Lumsden, A. Podlesnyak, Nat. Commun. 10(1), 698 (2019)
S.E. Nikitin, S. Nishimoto, Y. Fan, J. Wu, L.S. Wu, A.S. Sukhanov, M. Brando, N.S. Pavlovskii, J. Xu, L. Vasylechko, R. Yu, A. Podlesnyak, Nat. Commun. 12, 3599 (2021)
L. Vasylechko, A. Senyshyn, U. Bismayer, Perovskite-Type Aluminates and Gallates. Handbook on the Physics and Chemistry of Rare Earths, vol. 39, pp. 113, Elsevier (2009), Chap. 242
O. Buryy, Y. Zhydachevskii, L. Vasylechko, D. Sugak, N. Martynyuk, S. Ubizskii, K.D. Becker, J. Phys.: Condens. Matter 22, 055902 (2010)
L.S. Wu, S.E. Nikitin, M. Brando, L. Vasylechko, G. Ehlers, M. Frontzek, A.T. Savici, G. Sala, A.D. Christianson, M.D. Lumsden et al., Phys. Rev. B 99, 195117 (2019). https://doi.org/10.1103/physrevb.99.195117
M.A. Noginov, G.B. Loutts, K. Ross, T. Grandy, N. Noginova, B.D. Lucas, T. Mapp, J. Opt. Soc. Am. B 18(7), 931 (2001)
A. Bencini, D. Gatteschi, Electron Paramagnetic Resonance of Exchange Coupled Systems (Springer, Berlin, 1990)
Acknowledgements
We acknowledge valuable discussions with Stanislav Nikitin and Manuel Brando.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ehlers, D., Vasylechko, L., Medvecká, Z. et al. Magnetic Anisotropy in YbAlO\(_3\) Studied by Electron Spin Resonance. Appl Magn Reson 53, 1399–1405 (2022). https://doi.org/10.1007/s00723-022-01483-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00723-022-01483-x