1 Introduction

The EPR magnetic properties of tyrosyl radicals have been studied since the 1980s due to the importance of this paramagnetic species in biological processes [1,2,3,4,5,6,7]. Particularly, high-field/high-frequency EPR in combination with DFT calculations has been valuable to report on g\(_x\)-shifts, sensitive to the electrostatic and H-bonding environment [8,9,10]. Besides, ENDOR spectroscopy has been applied to elucidate the spin density distribution and radical conformation though the \(^1\)H hyperfine (hf) couplings [11,12,13,14,15]. Nevertheless, so far precise assignment of all internal \(^1\)H hf interactions remains obscure due to spectral overlap in the small coupling region (< 10 MHz).

Recent technological advancements have enabled the use of EPR and ENDOR spectroscopy at 9.4 T, corresponding to a microwave frequency of 263 GHz, which we have demonstrated on Y\(_{122}^\bullet\) in the \(\upbeta _2\)-subunit of E. coli RNR [16]. Due to its exceptional stability, this radical has served as a prototype for the characterization of tyrosyl radicals in various proteins and organisms. The EPR spectrum of Y\(_{122}^\bullet\) exhibits a prominent doublet splitting arising from the sizeable hf interaction of one of the \(\upbeta\)-methylene protons (H\(^{\upbeta _1}\)), which was already recognized over 50 years ago [17, 18]. Isotopic labelling experiments have been used extensively in related EPR studies [18] and ENDOR experiments [11], which also allowed the identification of the hf coupling parameters of the ring protons. Despite substantial efforts, no unambiguous determination of a smaller H\(^{\upbeta _2}\) hf interaction could be achieved. This issue has been interpreted as a consequence of the specific structure of the Y\(_{122}^\bullet\) radical, because the size of the H\(^{\upbeta }\) hf couplings depends on \(\cos ^2\) of the dihedral angle between the C–H\(^{\upbeta }\) bond and the ring plane, which is known as hyperconjugation and described by McConnell’s relation [19]. Hence, the H\(^{\upbeta _2}\) hf coupling would be expected to be very small if the nucleus is situated in the aromatic plane.

The observation of broad features in the 263 GHz ENDOR spectra of Y\(_{122}^\bullet\) prompted us to develop a statistical analysis of ENDOR spectra considering explicitly the possibility of signal drifts in long-term measurements [20]. The application of this “drift model” allowed for the presence of the broad features to be unambiguously established, owing to the availability of confidence intervals and statistical tests. Isotopic labelling experiments further demonstrated that the broad features are not observed upon deuteration of the \(\upbeta\)-methylene group and hence corroborated the assignment of the long-sought H\(^{\upbeta _2}\) hf coupling. This observation of a conformational distribution was consistent with previous ones from tyrosyl radical in model systems [21, 22]. The unexpectedly broad shape of these resonances provided the explanation for the previous failure to observe them: their broadness prevents distinguishing them from weak baseline distortions. Additionally, the partial overlap with resonances of the ring protons requires strong orientation selection for a clear observation, which is achievable only at very high magnetic fields.

In this report, we extend our analysis of the 263 GHz \(^1\)H-ENDOR spectra of Y\(_{122}^\bullet\) to a broader (70 MHz) radio frequency (RF) range, which includes the H\(^{\upbeta _1}\) resonances. Our recently developed “drift model” [20] is applied here for data processing, providing uncertainty estimates for the spectra. Spectral simulations demonstrate that the broad ENDOR line shapes of both H\(^{\upbeta }\) protons can be consistently reproduced by a distribution of ring dihedral angles and are not reconcilable with a single conformation. This result was supported by 94 GHz \(^2\)H ENDOR of Y\(_{122}^\bullet\) deuterated at the H-\(\upbeta\) positions.

2 Materials and Methods

Samples Wild-type (wt) RNR-\(\upbeta _2\) protein subunit was prepared in D\(_2\)O buffer containing 50 mM HEPES, 15 mM MgSO\(_4\) and 1 mM EDTA adjusted to pH 7.6. The concentration of the Y\(_{122}^{\bullet }\) radical in the sample was ca. 300 \(\upmu\)M, based on photometric assay. Protein solutions were loaded into Suprasil capillary tubes (VitroCom CV2033-S-100) with OD = 0.33 mm and ID = 0.2  mm, and subsequently shock frozen in liquid nitrogen. The sample capillaries were inserted into the precooled 263 GHz resonator immersed in a liquid nitrogen bath. Subsequently, the cold probe head was transferred into the cryostat, precooled to about 80 K. Samples contained typical volumes of about 50 nL.

For W-band \(^2\)H-ENDOR, Y\(_{122}^{\bullet }\) deuterated at C-H\(^{\upbeta _1}\) and C-H\(^{\upbeta _2}\) positions and incorporated in RNR-\(\upbeta _2\) protein as described in [20], was prepared at concentrations of ca. 300 \(\upmu\)M in H\(_2\)O buffer containing 50 mM HEPES, 15 mM MgSO\(_4\) and 1 mM EDTA. The protein solution was loaded into a Suprasil tube (Wilmad-LabGlass WG-213ST9S-RB) with OD = 0.9 mm and ID = 0.5  mm, and shock frozen in liquid nitrogen. The frozen sample was inserted into the resonator, precooled at 80 K inside the cryostat. The effective volume of the sample was around 1.5 \(\upmu\)L.

263 GHz Pulsed EPR/ENDOR Pulsed EPR and ENDOR spectra were recorded on a Bruker ElexSys E780 mm-band spectrometer equipped with a 100 mW microwave source (Virginia Diodes) and a Bruker cylindrical TE\(_{012}\)-mode ENDOR resonator. RF pulses were amplified with a 125 W RF-Amplifier (Amplifier Research, model 125W1000) for excitation at frequencies close to 400 MHz. A 50-Ohm semi-rigid coaxial cable (type RG 214U) leads the amplified RF to the ENDOR coil. After the coil, the cable is terminated by a 50 Ohm load to match the amplifier output and the RF transmission line. No matching circuit is used in this arrangement to permit broadband excitation.

To analyse and separate signal drifts due to thermal and mechanical instabilities during long-time signal acquisition, all ENDOR spectra were recorded in batches, where one batch contains the sum of 50 individual scans. Depending on the excitation position in the EPR line, a total of 200–300 batches was recorded. The Davies pulse sequence [23] was used to record spectra over a large (70 MHz) RF sweep range. The RF inversion pulse length was measured by Rabi nutation close to the \(^1\)H Larmor frequency (400 MHz) using \(^1\)H BDPA as reference sample, which has small hf couplings (< 10 MHz). Due to the weak ENDOR intensity of the Y\(_{122}^{\bullet }\) in the ± 35 MHz region around the Larmor frequency, the Rabi nutation could not be measured across the whole range. Instead, we have measured the RF coupling over 100 MHz as S\(_{11}\) reflection parameter, which is displayed in Fig. S1 and is flat within 0.3–0.4 dB. Therefore, the use of a single inversion pulse length over the whole range appears justified. Experimental settings and conditions: ESE (electron spin echo) detected spectrum: T = 5 K, \(\nu _\mathrm{mw}\) = 264.1 GHz, \(t_{\pi /2}\)/\(t_{\pi }\) = 32/64 ns, 1024 points, 10 shots/point, 10 ms shot repetition time (SRT), 1 scan. ENDOR: T = 5 K, \(\nu _\mathrm{mw}\) = 264.1 GHz, \(t_{\pi /2,\mathrm{mw}}\)/\(t_{\pi ,\mathrm{mw}}\) = 100/200 ns, \(t_{\pi ,\mathrm{RF}}\) = 60 \(\upmu\)s, SRT = 12 ms, 1 shot/point in stochastic acquisition, RF resolution: 175 kHz, RF points: 400. Number of batches: g\(_x\): 275, g\(_{xy}\): 300, g\(_y\): 283, g\(_{yz}\): 300, g\(_z\): 300. Acquisition times: 18–20 h/spectrum.

94 GHz pulsed EPR/ENDOR W-band ESE and ENDOR spectra were recorded on a Bruker ElexSys E680 spectrometer equipped with a 2 W microwave amplifier (Virginia Diodes) and a Bruker cylindrical TE\(_{011}\)-mode ENDOR resonator. The RF pulses were amplified by a 250 W RF-Amplifier (Amplifier Research, model 250A250A). RF excitation was performed at frequencies close to 22 MHz, which is the \(^2\)H Larmor frequency at 3.4 Tesla. The Mims pulse sequence [24] was applied. All spectra were recorded in batches, each containing the sum of 25 individual scans. Experimental settings and conditions: ESE: T = 20 K, \(\nu _\mathrm{mw}\) = 94.16 GHz, \(t_{\pi /2}\)/\(t_{\pi }\) = 10/20 ns, SRT = 10 ms, 1 scan, 30 shots/point. ENDOR: T = 20 K, \(\nu _\mathrm{mw}\) = 94.16 GHz, t\(_{\pi /2,\mathrm{mw}}\) = 10 ns, \(\tau\)=200 ns, t\(_{\pi ,\mathrm{RF}}\) = 70 \(\upmu\)s, SRT = 30 ms, 1 shot/point in stochastic acquisition, RF resolution: 16 kHz, RF points: 768. Number of batches: g\(_x\): 31, g\(_{xy}\): 36, g\(_y\): 50, g\(_{yz}\): 36, g\(_z\): 62. Acquisition time 5-10 hours depending on orientation.

Data Processing The recently presented “drift model” [20] was fitted to the raw data from the 263 GHz \(^1\)H ENDOR measurements. For this purpose, spectra were recorded in batches with real and imaginary signal parts obtained from quadrature detection, leading to a complex-valued raw data matrix \(Y_{b,\nu }\), where b indicates the batch number and \(\nu\) the index of the radio frequency. The ENDOR signal is mathematically described by Eq. 1, with the batch-dependent parameters \(\psi _b\) and \(\phi _b\) representing the offset and the magnitude of the ENDOR effect, respectively. The RF-dependent ENDOR signal \(\kappa _\nu\) is normalized according to Eq. 2. Additionally, the noise is modeled as a Gaussian component \(\epsilon _{b,\nu }\), described by real and imaginary standard deviations \(\sigma _r\) and \(\sigma _i\) and a correlation coefficient \(\rho\) (see Eq. 3).

$$\begin{aligned}&Y_{b,\nu } = \psi _b + \phi _b \kappa _\nu + \epsilon _{b,\nu } , \end{aligned}$$
(1)
$$\begin{aligned}&\sum _\nu \kappa _\nu =0 , \qquad \sum _\nu |\kappa _\nu |^2 =1. \end{aligned}$$
(2)
$$\begin{aligned}&\epsilon _{b,\nu } {\mathop {\sim }\limits ^{i.i.d.}} \qquad N(0,\Sigma ), \qquad \Sigma = \begin{pmatrix} \sigma _r^2 &{} \rho \sigma _r \sigma _i\\ \rho \sigma _r \sigma _i &{} \sigma _i^2\\ \end{pmatrix}. \end{aligned}$$
(3)

The ENDOR spectrum, defined as \(I_\nu\), is obtained by estimating \(\kappa _\nu\) from the matrix \(Y_{b,\nu }\), considering that the ENDOR signal should have zero imaginary part, defined as \(\omega _\nu\). However, we have found a weak wave-like baseline distortion in all imaginary parts of the 263 GHz ENDOR spectra. The distortion depends neither on the temperature nor on the sample and was attributed to some instrumental resonances of the detection scheme. This distortion might be correlated to the wave-like reflections observed in the S\(_{11}\) measurements (Fig. S1), however the frequency is slightly different. This phenomenon will be analyzed in greater detail in the future.

For now, the drift model approximates it as a cosine type function. This allows finding a rotation angle \(\lambda\) in \(e^{i\lambda } \kappa _\nu = I_\nu + i\omega _\nu\) that minimizes the \(l^2\) norm of the difference of \(\omega _\nu\) and a cosine-based estimate of the wave-like component obtained from \(\omega _\nu\). We refer to the minimizing \(\lambda\) as \(\lambda ^\mathrm {opt}\) and hence obtain the ENDOR spectrum \(I_\nu\) using Eq. 4 (see Fig. 1).

$$\begin{aligned} \begin{aligned} I_{\nu }&= \mathfrak {R} \left( e^{i\lambda ^\mathrm {opt}} \kappa _\nu \right) . \end{aligned} \end{aligned}$$
(4)

A detailed description of the Python implementation of the fitting procedure can be found in our recent report [20]. In this approach, maximum-likelihood estimators (indicated by a hat symbol) \(\widehat{\psi }_b\), \(\widehat{\phi }_b\) and \(\widehat{\kappa }_\nu\) are obtained, yielding also the most likely ENDOR spectrum \(\widehat{I}_{\nu }\). Based on these, the residuals \(R_{b,\nu }\) resulting from Eq. 5 can be assessed.

$$\begin{aligned} \begin{aligned} R_{b,\nu }&= Y_{b,\nu } - \widehat{\psi }_b - \widehat{\phi }_b \widehat{\kappa }_\nu . \end{aligned} \end{aligned}$$
(5)

Kolmogorov–Smirnov tests [25] for normality of \(R_{b,\nu }\) indicate that the drift model appropriately describes the present data, as the smallest corresponding \(p_\mathrm{KS}\)-value is 0.04 (in a total of 10 tests, i.e. for real and imaginary components of the residuals for all five spectral orientations). In agreement with the previous report, a total of 1000 bootstrap samples (per measurement) was used to perform bias correction of the estimators \(\widehat{\psi }_b\), \(\widehat{\phi }_b\) and \(\widehat{\kappa }_\nu\) and for the determination of the confidence intervals.

DFT Calculations The dependence of the hf coupling values of the H\(^\upbeta\) and H\(^\upalpha\) protons on the ring dihedral \(\delta\) (defined here by the atoms C\(^\upalpha\), C\(^\upbeta\), C\(^1\) and C\(^2\), atom numbering given in Fig. 3A) was investigated by DFT (Orca 4.0.1.2) [26, 27] with the dipeptide Ac-Tyr-Me serving as a small model system. The ring dihedral angle was varied in 5\(^\circ\) steps and for each structure the geometry was optimized. To resemble the peptide backbone structure in the protein, the backbone dihedral angles \(\Psi\) and \(\Phi\) (Ramachandran definition [28]) were additionally constrained to the respective values in the solid-state structure (PDB 1mxr, [29] ). A combination of the B3LYP functional [30,31,32,33] and the def2-TZVPP basis set [34] in conjunction with the D3BJ [35, 36] dispersion correction scheme was used. Hf parameters were subsequently calculated for the optimized structure employing the same parameters.

Spectral Simulation ENDOR spectra were simulated using a MATLAB routine developed in house [14, 16], which computes orientation selective ENDOR spectra based on the resonance frequencies from a first order Hamiltonian (high field approximation) for the hyperfine interactions. Calculated ENDOR lines were convoluted with a Lorentzian line shape (full width at half maximum: 100 kHz). Powder averaging was performed using a polar grid with increments of 0.257\(^\circ\) for the polar angle \(\theta\) (in range (0\(^\circ\), 180\(^\circ\))) and 360\(^\circ / (700\times \sin (\theta ))\) for the azimuth angle \(\phi\) (range [0,360\(^\circ\))), respectively.

Seven internal protons of the radical were included in the simulations. For the ring protons, pair-wise magnetic equivalence was assumed in agreement with all previous reports, and any dependence on the ring dihedral angle was disregarded. The hf parameters for the H\(^{3,5}\) protons in the simulation are [14]: \(A_{1,2,3}\) = –27.2 MHz, –7.9 MHz, –19.8 MHz, \(\alpha , \beta , \gamma\) = 25\(^\circ\)/125\(^\circ\), 0\(^\circ\), 0\(^\circ\). The hf parameters for the H\(^{2,6}\) protons in the simulation are: \(A_{1,2,3}\) = 4.9 MHz, 7.7 MHz, 1.7 MHz, \(\alpha , \beta , \gamma\) = –25\(^\circ\)/−125\(^\circ\), 0\(^\circ\), 0\(^\circ\). Euler angles \(\alpha , \beta , \gamma\) describe the rotation of the hf eigenframe to the g tensor frame in z, y’, z” convention, with positive values representing clockwise rotation when viewed along the respective rotation axis. In contrast, for the H\(^{\upbeta _1}\), H\(^{\upbeta _2}\) and H\(^\upalpha\) protons, the hyperfine tensors were obtained depending on the ring dihedral angle \(\delta\) by spline interpolation of DFT values (see Figs. 3 and S2), both for the eigenvalues and orientations (expressed as Euler angles). For the H\(^\upbeta\) protons, an empirical scaling factor of 0.955 was introduced to enhance the agreement with the experiment.

The ENDOR spectrum resulting from the distribution of ring dihedral angles was obtained by summation of spectra simulated for 70 individual rotamers. The corresponding ring dihedral angle values were chosen to linearly sample the cumulative distribution function of a normal distribution with mean \(\mu\) and standard deviation \(\sigma\) in the range [0.005, 0.995]. So far, best agreement was judged by visual comparison of the simulation within the error bars of the spectrum and was observed for \(\mu = 144^\circ\) and \(\sigma = 5^\circ\). The hf parameters corresponding to the dominant conformation (i.e. \(\mu = 144^\circ\)) are \(A_{1,2,3}\) = 60.2 MHz, 53.7 MHz, 55.5 MHz, \(\alpha , \beta , \gamma\) = 3\(^\circ\), 33\(^\circ\), –1\(^\circ\); \(A_{1,2,3}\) = 12.8 MHz, 7.0 MHz, 7.5 MHz, \(\alpha , \beta , \gamma\) = –81\(^\circ\), 135\(^\circ\), 66\(^\circ\); and \(A_{1,2,3}\) = 1.4 MHz, –2.1 MHz, –1.8 MHz, \(\alpha , \beta , \gamma\) = 83\(^\circ\), 106\(^\circ\), –40\(^\circ\) for the H\(^{\upbeta _1}\), H\(^{\upbeta _2}\) and H\(^\upalpha\) protons, respectively.

For simulations of the \(^2\)H-ENDOR spectra in Fig. 5, the same normal distribution of rotamer probabilities (Figs. 3B and S2B) has been applied. \(^2\)H hyperfine values for H\(^{\upbeta _1}\) and H\(^{\upbeta _2}\) were scaled by the factor \(\gamma {(^1H)}/\gamma {(^2H)}\). Additionally, the quadrupole couplings and their rotamer distributions (also centered around \(\mu = 144^\circ\) with \(\sigma = 5^\circ\)) (see Fig. S3) were considered.

3 Results and Discussion

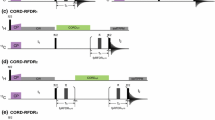
263 GHz \(^1\)H ENDOR spectra of the Y\(_{122}^\bullet\) in the protein \(\upbeta _2\)-subunit of E. coli RNR were recorded in a broad (70 MHz) RF range and at five different resonant positions of the EPR line (Fig. 1A). As ENDOR spectra contain baseline distortions due to signal drifts, it was important to separate the ENDOR signal from possible distortions prior to the analysis. For this goal, the spectra acquired in batches and stored in a large data matrix were processed using the “drift model” [20]. The procedure is demonstrated for a representative data set (g\(_x\)) in Fig. 1. The estimated ENDOR spectrum \(\widehat{I}_{\nu }\) is depicted in panel B with its 95 % confidence range. An approximately cosine-shaped distortion \(\widehat{\omega }_{\nu }\) (see panel C) is found in the imaginary signal of all data sets and could be separated from the ENDOR signal. Furthermore, a drift of the parameters \(\widehat{\psi }_b\), \(\widehat{\phi }_b\) over the course of the measurement becomes visible in panels D and E, respectively. Finally, partial correlation of the real and imaginary parts of the residuals \(R_{\nu ,b}\) is observed in panel F, which is a consequence of the employed quadrature detection. Kolmogorov–Smirnov tests indicate no statistically significant deviation of the residuals from normality when using a Benjamini–Hochberg correction [37] over the five measurements. These findings confirm that the drift model fits well to this new set of data without any modification. The clear drift of \(\widehat{\phi }_b\)—which represents the magnitude and phase of the ENDOR signal—highlights the issue of signal instability in ENDOR spectroscopy at this frequency. Despite this, processing the data with the “drift model” permits separating these drifts from the ENDOR spectrum and specifying confidence intervals. We anticipate that the availability of confidence intervals will also provide a means for estimating the uncertainty of information on distances and spin density distributions, which can be inferred from ENDOR spectra [38].

Fig. 1
figure 1

Results of data processing with the “drift model” on a representative dataset. A 263 GHz ESE spectrum of Y\(_{122}^\bullet\) in the protein \(\upbeta _2\) of wild-type RNR. ENDOR spectra were recorded at the five resonances indicated in the EPR line. The position for the representative dataset (g\(_x\)) is indicated in red. B Estimated ENDOR spectrum \(\widehat{I}_{\nu }\). C Estimated distortion \(\widehat{\omega }_{\nu }\). D, E Real (black) and imaginary (red) components of \(\widehat{\psi }_b\), \(\widehat{\phi }_b\), respectively. F Kernel density estimate of the residuals \(R_{\nu ,b}\). All variables correspond to those described in Eq. 1. Shaded grey regions indicate the point-wise confidence intervals (95 %), obtained from bootstrapping (Color figure online)

Full size image

For comparison, we display in Fig. 2 all five ENDOR spectra (recorded at the five positions in the EPR line) after processing with the “drift model” (right column) versus the spectra as obtained by standard averaging (left column). For a more detailed comparison, the spectra are plotted also in stack in Fig. S4. Standard averaging refers to simply summing up the spectra from all individual batches. Although the difference might appear small, the new method delivers improved S/N and confidence levels, which are important to judge possible broad features.

Fig. 2
figure 2

263 GHz \(^1\)H ENDOR spectra after processing with the “drift model” (right column, black) as compared versus spectra obtained by standard averaging (left column, blue). Shaded grey areas superimposed on the spectra in the right column indicate point-wise confidence intervals (95%) (Color figure online)

Full size image

In Fig. 2, the resonance lines of the H\(^{\upbeta _1}\) nucleus can now be observed at ca. ±30 MHz. They are more difficult to distinguish from the baseline due to their rather broad shape as compared with sharp features in the central part. The H\(^{\upbeta _2}\) couplings were assigned to weak and broad features centred at ca. ±5 MHz, as illustrated in Fig. 4 (upper row). Depending on the excitation position in the EPR line, partial overlap with other resonances occurs, which clearly prevents a straightforward recognition and underlines the difficulties of identifying this coupling in the past.

With confidence levels at hand, we note an asymmetry in the spectra which consistently exceeds the confidence levels. This asymmetry seems to correlate with the sign of the hf couplings, i.e. all low-frequency hf lines (including a visible effect in the broad H\(^{\upbeta _2}\) couplings) have less intensity except for the negative H3,5 couplings, which have reverse asymmetry pattern, i.e. the high frequency line has less intensity. This observation leads to the hypothesis that the asymmetry has a physical origin and is related to the extreme experimental conditions of low temperatures (T = 5 K) and the high magnetic field (9.4 Tesla). Whereas nuclear saturation is one possible explanation, nuclear spin polarization effects, posed by interplay of the electron-, nuclear- and cross-relaxations, might also contribute [39,40,41]. This effect is interesting, but goes beyond the scope of the current study and will be investigated in greater detail in the near future.

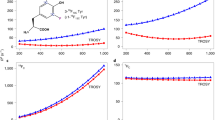
In our previous study we proposed that the broadening of the H\(^{\upbeta _2}\) coupling is consistent with a conformational distribution of the Y\(_{122}^\bullet\) in the \(\upbeta _2\) protein [20]. This model was based on previous observations in the literature, according to which the dihedral angles observed in various crystal structures of \(\upbeta _2\), in which the radical is reduced, vary by about 15\(^\circ\). A 5\(^\circ\)–10\(^\circ\) reorientation of the side chain was found in the g-tensor orientation of the radical in single crystals [29]. Moreover, a distribution of H\(^{\upbeta _2}\) couplings was reported from \(^2\)H ESEEM (electron spin echo envelope modulation) studies of tyrosyl radicals in frozen solution. To examine whether the proposed conformational distribution of the Y\(_{122}^\bullet\) is consistent with the full-width ENDOR spectra, we performed simulations considering a normal distribution of the ring dihedral angle \(\delta\) with mean \(\mu\) and standard deviation \(\sigma\). The normal distribution appeared as the simplest approximation to describe a distribution with only two parameters. The mean value determines simultaneously the positions of the center of both H\(^\upbeta\) resonances, while the standard deviation influences their widths. In our previous studies, the values \(\mu = 144^\circ\) and \(\sigma = 5^\circ\) were proposed [20], which were also examined here. To obtain the dependence of the hf coupling tensors of the \(\upbeta\)-protons (see Fig. 3A), spline interpolation of DFT-predicted values was used. The H\(^\upalpha\) nucleus was treated analogously. The predicted values and distributions of hfcs are depicted in Fig. 3B–D for these three nuclei at the investigated positions in the EPR line (cf. Fig. 1A). A significant broadening of the resonance lines is predicted, which is particularly pronounced for H\(^{\upbeta _2}\). For an accurate representation of the orientation selection, the four ring protons were included but are not plotted in this figure for clarity. No dependence of their hf parameters on \(\delta\) and pair-wise magnetic equivalence (H\(^{3,5}\) and H\(^{2,6}\), respectively) was considered, in agreement with previous reports [12, 14].

Fig. 3
figure 3

A Visualization of the variation of the ring dihedral angle \(\delta\) in a small model of a tyrosyl radical. B Probabilities for the rotamers with different dihedral angles \(\delta\) used to approximate the normal distribution with \(\mu = 144^\circ\) and \(\sigma = 5^\circ\). C Eigenvalues of the hyperfine tensors A for the H\(^{\upbeta _1}\) (teal), H\(^{\upbeta _2}\) (dark green) and H\(^{\upalpha }\) (purple) protons depending on \(\delta\), obtained by spline interpolation of DFT-derived values (\(A_1\): full lines; \(A_2\): dashed lines; \(A_3\): dash-dotted lines). D Simulated \(^1\)H ENDOR resonance line shapes for H\(^{\upbeta _1}\), H\(^{\upbeta _2}\) and H\(^{\upalpha }\) (same color code) resulting from the normal distribution of \(\delta\) in (B) and the hf values in (C) (Color figure online)

Full size image

Simulations, including all seven internal radical hf couplings, are superimposed upon the spectra in Fig. 4. For comparison, first simulations for a single rotamer (\(\delta = 144^\circ\), corresponding to the mean of the estimated distribution) are shown in the left column (orange). While the central positions of the H\(^{\upbeta }\) resonance lines are reproduced well, the simulated line shapes for H\(^{\upbeta _1}\) and H\(^{\upbeta _2}\) are clearly too narrow in all spectra. Considering the confidence intervals of the experimental spectrum, the possibility that the spectrum arises from a single conformation can effectively be ruled out. Variation of the ring dihedral \(\delta\) does not improve the agreement substantially, since narrow lines are always obtained for a single conformation. In contrast, the simulation using a normal distribution (Fig. 4, right column, red) exhibits far better agreement with the line shape and the confidence regions of the H\(^\upbeta\) resonances.

We note that the \(^1\)H ENDOR simulations in Fig. 4 do not account for all observed resonance lines in the central part of the spectra due to the contribution of external protons. As these resonances are retained even in the spectra of fully deuterated Y\(_{122}^{\bullet }\) [20], they likely result from weak interactions with neighboring amino acids. Finally, we note that the H\(^\upalpha\) proton was treated here in analogy to the H\(^\upbeta\) nuclei because a dependence of its hf coupling parameters on the ring dihedral angle \(\delta\) appears natural based on the atom connectivity. The simulated resonance positions (see also Fig. 3, peaks in purple) qualitatively agree with the experimental spectra. However, due to the proximity of these resonances to the matrix line and the overlap with resonances of nuclei in close-by amino acids, no clear conclusion can be drawn on H\(^\upalpha\).

The question might arise whether further sparsely populated radical conformations are present and can be distinguished. These cannot be ruled out but the current S/N in these \(^1\)H spectra prevents any further analysis. However, corresponding \(^2\)H-ENDOR experiments have the potential to reveal additional details, because the smaller gyromagnetic ratio of deuterons reduces the spread of the resonances across the RF axis, thus facilitating their detection. For this reason, we recorded W-band (94 GHz) \(^2\)H ENDOR spectra of Y\(_{122}^\bullet\) deuterated at H-\(\beta\) positions. The choice of the lower microwave frequency is related to some baseline distortions at 263 GHz in the region of the \(^2\)H Larmor frequency, which at the moment aggravate spectral analysis. Instead, the \(^2\)H-Mims ENDOR spectra at 94 GHz, illustrated in Fig. 5, clearly show sharp resonances of the H\(^\upbeta\)s. Simulations were performed with identical hf parameters also used for the \(^1\)H simulations in Fig. 4, but scaled here for deuterium. Additionally, a \(^2\)H quadrupolar coupling was considered, which was predicted by DFT as a function of the dihedral angle (Fig. S3). The simulations using the conformational distribution (Fig. 3B) reproduce the peak shapes very well. Visual inspection suggests no other ENDOR absorption, indicating the absence of less populated conformations. This hypothesis will be investigated by statistical analysis and an error model for W band data is in development.

Fig. 4
figure 4

Experimental 263 GHz Davies \(^1\)H ENDOR spectra of Y\(_{122}^\bullet\) after processing with the “drift model” (black, left and right columns) compared with the simulated spectra for a single radical conformation (dark red, left column) and a normal distribution of conformations (red, right column). The corresponding excitation positions in the EPR line are indicated in Fig. 1A. Shaded grey areas indicate point-wise confidence intervals (95 %). Simulation details are given in Sect. 2 (Color figure online)

Full size image
Fig. 5
figure 5

\(^2\)H W-band ENDOR spectra of Y\(_{122}^\bullet\) deuterated at the methylene position. Top: 94 GHz echo-detected EPR spectrum, showing the absence of the H\(^{\upbeta _1}\) splitting due to deuteration. The excitation positions used for ENDOR are marked. Bottom: Orientation selected Mims \(^2\)H ENDOR spectra of deuterated Y\(_{122}^\bullet\) (black). Simulations (red) are with identical hyperfine parameters as used for the \(^1\)H spectra but scaled for deuterium. Additionally, a conformational distribution of quadrupolar couplings for two methylene deuteriums as derived by DFT (Fig. S3) was included. A small discrepancy likely results from limited precision of  the DFT approach. Experimental details are given in Sect. 2 (Color figure online)

Full size image

4 Conclusions and Outlook

In this contribution we have presented the analysis of the H\(^{\upbeta _1}\) hf couplings in \(^1\)H 263 GHz ENDOR spectra of a representative protein tyrosyl radical, the E. coli RNR-\(\beta _2\) Y\(_{122}^\bullet\). Specifically, we have examined whether a model of conformational distribution, developed for the H\(^{\upbeta _2}\) resonances, was consistent with the full-width (70 MHz) ENDOR spectra and the H\(^{\upbeta _1}\) hf coupling. This model computed the distribution of H\(^{\upbeta}\) couplings as a function of the dihedral angle between the tyrosine plane and the direction of the C–H\(^{\upbeta }\) bond. For this goal, the 263 GHz \(^1\)H ENDOR spectra were recorded in batches and the so-called “drift model” was successfully applied for data processing. The analysis allowed for an estimate of the most likely signal, yielding statistically meaningful confidence intervals for the ENDOR spectra. This step was important to distinguish broad-distributed signals from baseline distortions.

The spectra were subsequently simulated using a normal distribution of ring dihedral angles for the tyrosyl radical. In agreement with preliminary studies, we have demonstrated that this distribution reproduces the shape of the H\(^{\upbeta _1}\) resonances reasonably well. We note that broad H\(^{\upbeta _1}\) resonances have also been recently observed in Q-band spectra of Y\(_{122}^\bullet\), in accordance with our finding, although those spectra were simulated with a single conformation [42]. Moreover, other molecular models might describe the observed distributions, for instance a distribution of spin density at C1 would also cause a similar effect in the hfs. However, our model appears the most favorable at the moment, given several reports in the literature about variation in dihedral angles of Y\(_{122}^\bullet\) in the crystal structures [29, 43,44,45] and of tyrosyl radical produced in vitro [21, 22]. Moreover, our results highlight the importance of predicting molecular conformations (and their possible broad distributions) for understanding hyperfine spectra, which in turn provide valuable information on structural heterogeneities and conformational distributions of biologically relevant paramagnetic intermediates.

Finally, we emphasize that our current analysis considers only Y\(_{122}^\bullet\) in the isolated \(\upbeta _2\)-subunit of E. coli RNR. The conformational distribution established on this sample provides a starting point for future studies focusing on the corresponding behaviour of Y\(_{122}^\bullet\) and intermediately formed radicals in catalytically active proteins.