Abstract
This article presents an analysis of spurious signals’ influence on automatic frequency control (AFC) in EPR spectrometers. The primary source of spurious signals is leakage across the circulator in the microwave bridge. Additionally, the signals reflected from connectors in the line between the circulator and the resonator modify that signal. Spurious signals may degrade the performance of AFC, significantly offsetting lock points from the center frequency of the resonator. The offset’s size depends on the parameters of the resonator and the amount of the circulator isolation. It can be minimized by the appropriate use of a phase shifter located in the line between the circulator and the resonator. Another way to avoid these problems is to introduce a leakage compensation arm to the microwave bridge.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
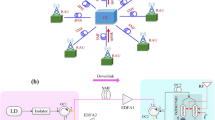
This article is concerned with automatic frequency control (AFC) systems used to lock the frequency of a microwave generator to the resonant frequency of the resonator in an electron-paramagnetic-resonance (EPR) spectrometer. Many different AFC systems are used in EPR spectrometers, ranging from the DC system introduced by Pound [1] to systems that use frequency modulation of the microwave generator to generate the AFC error signal (i.e. [2]). An excellent overview of AFC systems can be found in Wilmshurst’s monograph [3]. A critical factor in the AFC’s functioning is the correct alignment of the phase shifters located in the microwave bridge’s different arms. Figure 1 illustrates one example of a microwave system that we will discuss in this article. To avoid microwave phase problems, particularly in the reference arm, Hyde and Gajdzinski [4] proposed using the sum of squares of the mixer’s I and Q outputs to create an AFC error signal when using 70 kHz frequency modulation of the microwave source. In this way, the dependence of the AFC on the phase of the reference signal is avoided. The authors of this article noted the problem of using a circulator with low isolation. It creates a leakage signal, which adds to signals reflected from connectors in the resonator arm. To eliminate the problem of the phases of the microwave bridge signals, the authors suggest placing a phase shifter in the resonator arm. This suggestion was not implemented by them.
Krymov and Gerfen [5] carried out a detailed analysis of spurious signals’ influence, resulting from circulator leakage and reflections in the resonator transmission line, on the EPR signal. These authors also suggest placing a phase shifter in the resonator arm to phase the signals correctly.
The main problem generated by spurious leakage is the shift of the AFC lock point from the resonator’s resonant frequency. This study’s primary purpose is to analyze the magnitude of this shift as a function of resonator parameters as well as amplitude and phase parameters of the spurious signal. The analysis included the placement of the phase shifter in the resonator arm. Measurements of the offset’s value were also made, depending on the phase shifter settings.
The implementation of the concept of minimizing spurious signals using an additional arm is also presented. The originator of this idea was Piotr Leśniewski and Tadeusz Walczak from the laboratory of Professor Harold Swartz from Dartmouth College.
2 Theoretical Considerations
The amplitude and phase of the signal with frequency f reflected from the resonator with center frequency fR depends on the value of the reflection coefficient Γ at the frequency difference \(\Delta f=f-{f}_{R}\) as follows [4, 6]:
where β is the resonator coupling coefficient (the ratio of the transmission line characteristic impedance to the equivalent resistance of the resonator) and Q0 the unloaded Q.
The convenient phasor form of Eq. (1) is the following:
where \(\Lambda \left(\Delta f\right)=arg\Gamma \left(\Delta f\right)\), \(\left|\Gamma \left(\Delta f\right)\right|\) is the magnitude of Γ.
Two ways of implementing the AFC system are analyzed below. The first method uses a quadrature mixer, similar to Hyde and Gajdzinski [4]. The second method uses a diode detector, for example as Pechan et al. [7] or Kozioł et al. [8]. These two methods are shown schematically in Fig. 1.
3 Using Quadrature Mixer for AFC
The microwave signal with angular frequency ω = 2πf, incident on the resonator, \({\nu }_{\mathrm{inc}}\left(t\right)={V}_{0}\mathrm{cos}\left(\omega t\right)\), after reflection from the resonator, from port 2 to port 3 of the circulator (Fig. 1), reaches the input of the quadrature mixer with modified amplitude and phase which can be represented by the real part of the exponential function called the analytic representation as follows:
In-phase and quadrature components have the following forms:
where angle Θ represents the phase difference between the mixer LO signal and the mixer input signal, \({\nu }_{\mathrm{refl}}\left(t\right)\).
The in-phase and quadrature components of the mixer outputs can be calculated using angle sum identities for cosine and sinus:
The circulator plays an essential role in the microwave bridge by directing the generator’s signal to the resonator, the signal reflected from the resonator directly to the mixer (Fig. 1). An important parameter is the circulator isolation between ports 1 and 3. As a result of low isolation, the generator signal leaks and a leakage signal \({\upsilon }_{\mathrm{leak}}\left(t\right)\) is added to the signal \({\nu }_{\mathrm{refl}}\left(t\right)\) at the mixer input port as follows:
where Isol is the circulator isolation coefficient and \(\phi\) the phase in relation to the phase of the LO signal in a quadrature mixer.
To simplify the argument, we assume that the spurious leakage across the circulator has a constant value. Note that reflected waves from connectors in the line between the circulator and the resonator may modify the leakage level [4].
As a result of addition, Eqs. (6) and (7) will take the following form:
As can be seen from these equations, the mixer output voltages’ dependence on the frequency difference Δf is very sensitive to the phase difference of the LO signal and the mixer input RF signal represented by angle Θ. To become independent from this angle, Hyde proposed using the sum of squares of VI and VQ. When the difference between the RF and LO phase angles is 0°, then
It is easy to implement using direct digitization of these mixer outputs.
We should emphasize that this simple form of the equation only applies when the LO signal and that part of the RF signal reflected by the resonator without leakage signal are in phase in the mixer. Otherwise, the dependence of \({V}_{out}^{2}\) on the frequency offset Δf will depend on both the angle Θ and φ as follows from Eqs. (9) and (10).
Figure 2 illustrates the quadrature mixer output voltages’ dependence on the frequency offset Δf for different angular parameters used in Eqs. (9 and 10). It allows the consideration of various possibilities for designing an AFC system in relation to the center frequency of the resonator. The most straightforward approach would be a DC AFC using the VQ signal visible in row (a) of Fig. 2. The presented dependence of VQ on frequency has the desired discrimination properties. Unfortunately, they are dependent on angles Θ and φ, which can alter the DC AFC system’s lock point in the presence of circulator leakage.
Quadrature mixer output voltages, VI and VQ, and their derived functions \(\sqrt{{V}_{I}^{2}+{V}_{Q}^{2}}\) and \({V}_{I}^{2}+{V}_{Q}^{2}\) depending on the frequency offset Δf according to Eqs. (7 and 8). The following values of the Q0 and fR parameters were used: 360 and 1.15 GHz, respectively. Row (a) shows simulations for a perfect circulator, Isol equals 0, and angle Θ equals 0°. For row (b), Isol equals 0, and Θ equals 300. For row (c) Θ equals 0°, Isol equals 0.2 (− 14 dB) and φ equals − 40°. The solid lines relate to β = 1, the dashed lines to β = 1.2, and the dotted lines to β = 0.75
A more appropriate AFC system is one using frequency modulation of the generator or resonator. The AFC signal generated in this way at the mixer output is proportional to the curves’ slope in Fig. 2, i.e., mathematically to the first derivatives of V’s dependence on the frequency Δf.
They have the discrimination properties suitable for AFC as long as the signals LO and RF are in phase (Θ is 0) in the mixer. The Θ angle shifted from zero will move the AFC lock point away from the resonator’s center frequency (see row (b) in Fig. 2). The phase shifter in the reference arm can set the angle Θ, which complicates the measurement procedure. Hyde and Gajdzinski [4] proposed using the sum of the squares of the mixer output voltages VI and VQ for the AFC system (see row (b) in the last column of Fig. 2) to avoid these problems. Such an AFC circuit is independent of the reference-arm phase. Row (c) of Fig. 2 illustrates a problem in the functioning of AFC in the presence of spurious leakage across the circulator. It causes a shift of the lock point of AFC depending on the signal’s leakage value and its phase relative to the signal reflected from the resonator. Hyde and Gajdzinki also noticed this problem. To remove it, they proposed using a phase shifter in the resonator arm (see Fig. 1) to set a ReΓ in phase with spurious leakage.
We performed computer simulations to investigate the effect of spurious leakage on the magnitude of the AFC lock point shift away from the resonator’s center frequency. For that, we used the iterative method implemented in Mathcad 15 to find values of Δf and β for which the sum of squares of VI and VQ reaches zero at a given value of angle Θ according to Eqs. (9–11). Usually, it was enough to repeat a sequence of program instructions three times to obtain a sufficiently small \({V}_{out}^{2}\left(\Delta f\right)\) value. Figure 3 presents the results of simulations for three different values of angle \(\phi\) using typical values of L-band bridge parameters shown in the figure caption. The values of Δf and β obtained from the simulation can be perfectly fitted (determination coefficient R2 equals 1.0) to the following sinusoidal functions:
where AΔf and Bβ represent amplitudes of the sine wave, and A and B are their mean values.
Influence of the angle Θ on the frequency offset Δf (a) and a corresponding value of the coupling coefficient (b) for three values of the angle φ [see Eqs. 7 and 8)]: the dots represent 0°, 45° squares, and 900 triangles. Points show simulated values, and solid lines show sine fit. The coefficient of determination for these fits is 1.0. The Q value is 360, and the circulator isolation is − 14 dB. The center frequency of the resonator is 1.15 GHz
We used these functions to analyze experimental data. Equation (12) shows that the AFC lock point will lie at the center frequency of the resonator, i.e., Δf will be 0, when the sum of the angles Θ and \(\phi\) will be zero or the positive or negative values of multiples of π. It suggests the following procedure for setting the phases in the bridge. First, adjust the phase of the reference arm (Δφ3 in Fig. 1) to get zero for the \(\phi\) angle and then change the RF signal phase (Δφ1 in Fig. 1) to be in-phase with the LO signal in the mixer.
Table 1 shows the calculated values of parameters AΔf, Bβ, and B for Eq. (12) for typical resonators in the L-band [9], X-band [10, 11], and W-band [12].
The calculation data presented in Table 1 allows for the formulation of the following comments. An important factor influencing the offset size of the AFC lock points is the circulator isolation amount. The worsening of this isolation, e.g., from 20 to 10 dB, increases the offset by 3.5 times close to the leakage signal voltage change (3.16 times). The magnitude of AΔf is inversely proportional to the Q of the resonator. In turn, the magnitude of the AΔf parameter is proportional to the resonant frequency of the resonator. These simple dependencies are quite intuitive and make it easier to evaluate changes in the AFC lock point offset when changing resonator parameters. It is worth noting that the sinusoid’s parameters describing the resonator coupling coefficient [Eq. (12)] depend only on the circulator isolation’s size and not on the resonator parameters.
4 Using Diode Detector for AFC
The second method of AFC implementation discussed in the present work is to use a diode detector instead of a mixer [8]. It uses a Schottky diode detector to detect the signal at point (b) shown in Fig. 1. In the square-law region, the detector’s output voltage is roughly proportional to the square of the input voltage.
As with the mixer, the incident microwave signal reflected from the resonator is
And the spurious microwave signal at the input of the diode detector is as follows:
where \(\phi\) is the phase difference between \({\upsilon }_{\mathrm{refl}}\left(t\right)\) and \({\upsilon }_{\mathrm{leak}}\left(t\right)\) at the input of the diode detector when \(\Lambda \left(\Delta f\right)=0\).
At the detector input, we have the sum of these two sine waves of the same frequency and different amplitudes and phases. This sum is also a sine wave of the same frequency and, as follows from trigonometric identity, takes the form of the following equation:
The output of the diode detector is proportional to the square of the input signal,\({{ V}_{det}\left(\Delta f\right)}^{2}\). This equation is similar to Eq. (11) except that the angle ϕ has a different meaning. Equation (11) represents the spurious signal phase with respect to the LO phase at the mixer. The angle ϕ in the last equation is the spurious signal phase with respect to the RF signal reflected from the resonator. The dependence of \({V}_{det}\) on the frequency offset, \(\Delta f\), is therefore the same as shown, for example, in row (c), column 3, and 4 in Fig. 2.
5 Generation of AFC Error Signal
In both detection methods, the AFC error signal is generated by modulating either the generator frequency (current work) or the resonator resonant frequency [8]. It corresponds to the frequency offset modulation, Δf in Eq. (11) and Eq. (15), respectively, for the mixer and diode detector. The amplitude of the AFC error signal is proportional to the derivative of those functions.
This way, it generates the AFC discriminator curve. For a small frequency offset of several hundred kHz, the inclined lines intersect the frequency offset axis at the point where the AFC locks. This line represents the AFC discriminator curves.
6 Instrumentation
Experimental studies of AFC functioning depending on the phase shifter settings were carried out on the home-built L-band microwave bridge. The phase shifter was placed in the resonator arm, as shown in Fig. 1. The shifter used in these measurements (Arra Mod. 9428A) had a measured attenuation of approx. 0.1 dB and Voltage Standing Wave Ratio (VSWR) below 1.03 in the entire phase range (0–70 deg). SMA to SMA adapters added in series with the phase shifter increased its angular range. As measured at 1.15 GHz, each adapter produced exactly a 50 deg phase shift. In this bridge, the quadrature mixer output voltages VI and VQ were directly digitized and then further mathematically processed to produce an AFC error signal. A bridge presented in an earlier publication [8] used a diode detector to generate the AFC error signal (see Fig. 1). AFC lock points were also measured for the commercial Bruker CW Imaging System ELEXSYS E540L L-band spectrometer using the original E540SC surface coil to compare the different systems.
7 Results and Discussion
7.1 Using the Phase Shifter
AFC lock points were measured in the L-band using two different resonators. The first is a surface coil developed in Professor Swartz’s laboratory [9, 13], and the second is a home-built 4 mm loop-gap resonator [11]. Figure 4 presents sample graphs of experimental AFC lock points depending on the phase shifter settings for the surface coil. The perfect fit of the sinusoid to the experimental points is noticeable. Table 2 presents detailed sinusoidal parameter values. These experimental data confirm the above calculation results that lowering the surface coil’s Q, i.e., using a salt solution, leads to an increase in the range of changes in AFC lock points (amplitudes of sinusoids). A twofold decrease in Q causes an approximately two-fold increase in the amplitude of changes in AFC lock points. The presence of saline also causes the resonant frequency of the surface coil to drop.
AFC lock points as a function of the phase shifter settings. Points represent experimental data obtained for an empty surface coil (upper plot) and in the presence of a 1.5 mL Eppendorf tube filled with saline (lower plot) using a quadrature mixer. The solid line represents the sinusoidal fit to the experimental points
The change of the resonant frequency is one reason why the sine wave phase changes by about 80 degrees. Also, for the loop-gap resonator, a very similar sine wave phase shift occurs under the saline influence, as shown in Table 2. The four data sets shown in the first four rows of the table were measured with a home-built microwave bridge. The last row of the table shows the surface coil data measured with a Bruker spectrometer. Interestingly, the range of AFC lock points changes, in this case, is the same as for the surface coil measured in our spectrometer. It proves a similar level of spurious leakage signal in both spectrometers.
A consequence of the frequency changes of AFC lock points is a change in the EPR lines position in the magnetic field, as illustrated in Fig. 5. The peak-to-peak range of these changes, recorded with the home-built microwave bridge, is 0.7 Gs, which corresponds to a change in the microwave frequency by 2 MHz. These are not large changes in the field position of the EPR line compared to the TEMPOL line width. In these measurements, a thin capillary (ID 0.7 mm) filled with an aqueous solution of the spin-label practically does not change the 4 mm loop-gap resonator’s Q. The situation is different in animal EPR studies, when the Q of the resonator drops sharply, as a consequence of which the range of AFC lock points changes to several MHz. It causes the field position of the EPR lines to shift more than their widths.
The position of the center line of the spin label (TEMPOL) in the magnetic field, depending on the settings of the phase shifter, is marked with dots. The solid line represents the fit to the sine wave. The peak-to-peak amplitude of the sinusoid is 0.7 Gs, the mean value is 401.2 Gs, and the coefficient of determination, R2, equals 0.91
It is necessary to explain the twofold difference in the phase values range in Figs. 3 and 4. In the first case, it is the actual phase change, and the second is the setting of the phase shifter. In the latter case, the RF signal in the resonator arm passes through the phase shifter twice, causing the phase to change twice concerning the phase shifter setting.
7.2 Cancelation of Spurious Leakage
Another way to avoid the consequences mentioned above of low circulator isolation is to cancel the spurious signals. The problem of leakage signals appeared a long ago in Continuous Wave (CW) radars [14] and nowadays in wireless communication [15]. In single-antenna CW radar, the challenge is achieving sufficient isolation between transmitter and receiver. One solution to obtain adequate isolation is using a Reflected Power Canceller (RPC). The authors of the mentioned above publication used a vector modulator as RPC. It consists of two separate channels, I and Q, which operate independently. We implemented a similar approach in the current work.
Similarly, in wireless communication, the same antenna transmits and receives the signal using a full-duplex transceiver system design operating with a single channel, i.e. [16]. Such a system can be implemented with a circulator, similarly to the microwave bridge in the EPR spectrometer, where a resonator plays the antenna’s role. A wealth of experience in wireless communication can, therefore, help to improve the EPR spectrometer. Like the radar systems, the significant problem is providing adequate isolation between transmitter and receiver ports. RF cancelation is an absolute necessity in digital systems to avoid analog-to-digital converters’ saturation (ADC) [8].
Implemented by us in the L-band house-built microwave bridge, the leakage cancelation module (LCM) is a vector compensator (Fig. 6). It works by adding two orthogonal signals whose amplitudes can vary independently from − 1 to + 1. In this way, it is possible to obtain a signal with adjustable amplitude and phase over the full range of angles (0°–360°). The compensator consists of a 2-way-90° power splitter at the output of which the signals are shifted by 90º. The signals are then directed to the balanced mixer’s inputs, which change the output signals’ amplitudes in the range − 1 to + 1. The power combiner adds together the signals from the modulator outputs. The low pass filter removes the high-frequency components of the summed signals.
The circuit used to compensate for the spurious signal caused mainly by poor isolation of the circulator. The meaning of the abbreviations used in the diagram: SPI (Serial Peripheral Interface), CPLD (Complex Programmable Logic Device), LPF (Low Pass Filter), DAC (Digital to Analog Converter). Key components from Mini-Circuits: power splitters (QCN-19 and SCN-2-11), double balanced mixers (ADE-5), and Low Pass Filter (LFCN-1400); from Analog Devices: DAC (AD8582A); from Xilinx: CPLD (XC2C128-7TQ144C)
The 12-bit digital-to-analog converter (DAC) generate the mixer control voltages. The DAC input signals produce a Complex Programmable Logic Device (CPLD) controlled from a microprocessor through a serial peripheral interface. The input signal’s power is 10 dBm, and the output signal power can be set in the range from − 27 dBm to − 9 dBm.
Figure 7 demonstrates the effects of using a leakage compensator. The sine wave’s peak-to-peak amplitude decreased almost 30 times, from 2.8 MHz to 100 kHz. It corresponds to an increase of circulator isolation by about 30 dB. Minimizing the spurious leakage signal level was carried out manually by measuring the microwave power level at the output (b) in Fig. 1. It would be desirable to automate this operation using available digital control of the LCM. In a practical system, the LCM must be a closed-loop with sufficient gain and bandwidth to track the leakage variations. Using such a system, the authors of the mentioned above publication [14] achieved 40 dB of power cancelation in an X-band radar system.
8 Conclusions
When designing microwave bridges, particular care is taken to ensure that the lengths of the two microwave paths from the source to the mixer are comparable, one through the circulator to the resonator and from the resonator to the mixer, and the other through the reference arm (Fig. 1). It ensures that the microwave signals arriving in these two paths will maintain constant mutual phase relations in the mixer, regardless of the microwave frequency. The present work pays additional attention to the spurious signal’s phase relations to the LO signal and the microwave signal reflected from the resonator. As the paths of the last two signals can be aligned, it is impossible to do the same for spurious signals coming from different places in the microwave system. For this reason, AFC will lock to a point off the resonator resonance.
The article discusses two solutions to work around the phase problem. The first solution is to insert a phase shifter into the resonator arm. This shifter’s appropriate setting allows the AFC system to lock the resonant frequency of a microwave oscillator to the resonant frequency of a sample containing a microwave resonator. With the wrong setting of the phase shifter, these two frequencies are moved apart. This frequency consistency can be achieved when a quadrature mixer or a diode detector is used to detect the AFC error signal. A more straightforward solution in aligning the phases is using a diode detector to detect the AFC error signal.
The second method of avoiding the unfavorable consequences of spurious signals presented in the present work is their elimination with the leakage cancelation arm. This way, one can eliminate the negative consequences of low isolation of the circulator or spurious reflections from the resonator arm.
References
R.V. Pound, Electronic frequency stabilization of microwave oscillators. P Ire 34, W89–W89 (1946)
A. George, D. Teaney, Transistorized lock-in for klystron automatic frequency control. Rev Sci Instrum 31, 997–998 (1960)
T.H. Wilmhurst, Electron Spin Resonance Spectrometers (Springer, US, 2013).
J.S. Hyde, J. Gajdzinski, Electron-paramagnetic-res automatic frequency control-circuit with field-effect transistor (Fet) microwave amplification. Rev Sci Instrum 59, 1352–1356 (1988)
V. Krymov, G.J. Gerfen, Analysis of the tuning and operation of reflection resonator EPR spectrometers. J Magn Reson 162, 466–478 (2003)
T. Hays, Cavity Analysis By Reflection, in A Treatise on Transient Response, Internal Notes Laboratory of Nuclear Studies (Cornell University, Ithaca, NY, 1994)
M.J. Pechan, J. Xu, L.D. Johnson, Automatic frequency control for solid-state sources in electron spin resonance. Rev Sci Instrum 63, 3666–3669 (1992)
J. Kozioł, P. Rajda, R. Rumian, T. Oleś, P. Budzioch, R. Gurbiel, W. Froncisz, Continuous wave electron paramagnetic resonance L-band spectrometer with direct digitalization using time-locked subsampling. J Magn Reson 322, 106870 (2020)
H. Hirata, T. Walczak, H.M. Swartz, Characteristics of an electronically tunable surface-coil-type resonator for L-band electron paramagnetic resonance spectroscopy. Rev Sci Instrum 72, 2839–2841 (2001)
R. Weber, EPR Resonators, in User Service Training Course (Bruker Biospin Corp, 2002). https://www.cif.iastate.edu/sites/default/files/uploads/EPR/Resonators.pdf
W. Froncisz, J.S. Hyde, The loop-gap resonator—a new microwave lumped circuit electron-spin-resonance sample structure. J Magn Reson 47, 515–521 (1982)
J.W. Sidabras, R.R. Mett, W. Froncisz, T.G. Camenisch, J.R. Anderson, J.S. Hyde, Multipurpose EPR loop-gap resonator and cylindrical TE011 cavity for aqueous samples at 94 GHz. Rev Sci Instrum 78, 034701 (2007)
H. Hirata, T. Walczak, H.M. Swartz, Electronically tunable surface-coil-type resonator for L-band EPR spectroscopy. J Magn Reson 142, 159–167 (2000)
P. Beasley, A. Stove, B. Reits, B, As, solving the problems of a single antenna frequency modulated CW radar, in IEEE international conference on radar. (IEEE, 1990), pp. 391–395
P. Nouri, RF system model for in-band full-duplex communications, in Master’s Thesis (University of Oulu, Finland, 2016)
S. Khaledian, F. Farzami, B. Smida, D. Erricolo, Inherent self-interference cancellation for in-band full-duplex single-antenna systems. Ieee T Microw Theory 66, 2842–2850 (2018)
Acknowledgements
On the occasion of Professor Harold M. Swartz’s 85th birthday, we would like to express our gratitude for the many years of acquaintanceship and cooperation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kozioł, J., Froncisz, W. Functioning of EPR Automatic Frequency Control in the Presence of the Circulator’s Spurious Leakage. Appl Magn Reson 53, 207–220 (2022). https://doi.org/10.1007/s00723-021-01357-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00723-021-01357-8