1 Introduction

Chemically induced dynamic nuclear polarization (CIDNP) [1,2,3,4,5,6,7] is a spin chemistry technique, which is used to study elusive radical intermediates of chemical reactions and to enhance NMR signals of their diamagnetic reaction products. Typically, the origin of CIDNP is explained in the following way on the basis of the radical pair mechanism. In this mechanism, recombination of a radical pair (RP) is considered. RPs are often formed in a specific electron spin state, which is inherited from a precursor molecule. For instance, RPs can be formed after bond cleavage in a photo-excited molecule or in the course of an electron transfer reaction involving an excited dye molecule in its electronic singlet or triplet state. Recombination of the RP is also a spin-selective process, occurring at a different rate for RPs in their singlet and triplet states. Owing to this spin-selectivity, singlet–triplet interconversion becomes important, as it has an impact on the rate of RP recombination. The interconversion rate can be affected by external magnetic fields (static or oscillating) and also by local fields in the radicals, originating from hyperfine couplings to their magnetic nuclei. As a consequence, the RP reactivity does depend on the nuclear spin state: in some states, RPs react faster and in some states they react slower. This gives rise to nuclear “spin sorting” [2, 8] by the chemical reaction, such that the reaction product is enriched or depleted in certain nuclear spin states, i.e., the reaction product is formed in a non-equilibrium spin state. The resulting spin polarization is termed CIDNP and it gives rise to significant NMR signal enhancements. NMR measurements of CIDNP and analysis of the field dependence and time dependence of polarization allows one to determine magnetic parameters and reactivity of RP intermediates, which are often not accessible by other spectroscopic methods. Although NMR is not suitable to detect short-lived species directly, CIDNP encoded in the reaction products can be treated as a “frozen signature” [7] of transient radicals.

In this article, we want to discuss one of the peculiarities of CIDNP, which is rarely addressed. Typically, it is stated in the literature that CIDNP manifests itself in non-equilibrium populations of the spin states of reaction products. However, in some cases, one must take into account the fact that also coherences between these states can be formed. For a long time, this has been ignored, most likely, for the reason that such coherences are difficult to detect directly. Until recently, this effect has been discussed in a limited number of papers, notably, in the work by Ernst and coworkers [9], in which such coherences were detected for the first time. Salikhov has discussed [10] such effects from a more general perspective, also paying special attention to the case of EPR of spin-correlated RPs, where Zero-Quantum Coherences (ZQCs) are formed and can be detected by EPR methods. Such effects have been observed [11,12,13,14] in photosynthetic reaction centers by pulsed EPR methods. Jeschke [15] has also discussed the possibility of detecting such coherences, which he named CIDNC (chemically induced dynamic nuclear coherence). Although the formation of spin coherences is rarely discussed, our CIDNP experiments have shown that formation of coherent hyperpolarized states is a ubiquitous phenomenon at low magnetic fields. Here it should be noticed that when we say “low” field, we mean the regime of strong coupling of the relevant spins, whereas the term “high field” is used when high spectral resolution is reached (discrimination of individual spin positions is possible). By the regime of ‘‘strongly coupled nuclear spins’’, we mean that the difference in frequency caused by their Zeeman interaction with the external magnetic field is smaller than or, at least, comparable to their scalar spin–spin interaction, J. Detection of nuclear spin coherences and measurement of their temporal evolution requires some effort (as discussed below), but their presence often gives rise to evident consequences, namely to efficient polarization transfer [16,17,18] among coupled spins (which is manifest even when the actual time dependence of polarization is difficult to discern). Typically, such coherent effects are most pronounced at Level Anti-Crossings (LACs) [17, 19] of the nuclear spin levels of the polarized reaction product. Careful examination [16, 17, 19] reveals that polarization transfer is indeed a coherent phenomenon, which can be efficiently exploited to polarize spins, which do not acquire CIDNP directly. The same concepts can be applied to transfer hyperpolarization of other kinds, notably to Para-Hydrogen-Induced Polarization (PHIP) [20, 21].

Here we provide a general consideration of coherent phenomena in CIDNP and support it by examples, obtained for a dipeptide, namely tryptophan–tryptophan (Trp–Trp). The examples presented here for Trp–Trp are not limited to this particular system, but are rather aimed at illustrating more general phenomena.

2 General Considerations

As mentioned above, the origin of CIDNP is the dependence of singlet–triplet interconversion on the nuclear spin state. When this is the case, different nuclear spin states, \(|i\rangle\) and \(|j\rangle\), acquire different population in the diamagnetic reaction product, \(p_{i} \ne p_{j}\) (the state population is given by the corresponding diagonal element of the density matrix of the reaction product, \(p_{i} = \rho_{ii}\)). However, this is not the only consequence of singlet–triplet mixing in the RP. Generally speaking, when the RP spin Hamiltonian \({\hat{\mathcal{H}}}_{{{\text{RP}}}}\) has different symmetry properties compared to the spin Hamiltonian \({\hat{\mathcal{H}}}\) of the reaction product, one should expect also formation of the spin coherences \(\rho_{ij}\) between the states \(|i\rangle\) and \(|j\rangle\). We would like to support this statement by giving one example.

Let us consider an RP with two nuclear spins, denoted as \(I_{1}\) and \(I_{2}\). We assume that in the RP both nuclei belong to the same radical and have strongly different hyperfine couplings, \(A_{1} \ne A_{2}\); in the ultimate case, we can set \(A_{2} = 0\). The RP spin Hamiltonian of the RP then takes the form (the electron spins are denoted as \(S_{a}\) and \(S_{b}\)):

$$ {\hat{\mathcal{H}}}_{{{\text{RP}}}} = \omega_{a} \hat{S}_{az} + \omega_{b} \hat{S}_{bz} + A_{1} \left( {{\hat{\mathbf{S}}}_{a} \cdot {\hat{\mathbf{I}}}_{1} } \right) + A_{2} \left( {{\hat{\mathbf{S}}}_{a} \cdot {\hat{\mathbf{I}}}_{2} } \right). $$
(1)

Here \(\omega_{a,b}\) stand for the electronic Zeeman interactions with the external field. We consider the case of an RP in a liquid solution of normal viscosity, where anisotropic interactions can be omitted (as they average out by molecular tumbling); furthermore, electron–electron coupling does not significantly affect the polarization formation [22, 23].

The Hamiltonian (1) dictates the RP spin evolution. In the case \(A_{2} = 0,\) the evolution does not depend on the state of the second nucleus. This means that the populations of the states of the reaction product are independent of the state of the second nucleus as well. Hence, if we introduce the elements of the density matrix of the reaction product as \(\rho_{{i_{1} i_{2} ,j_{1} j_{2} }}\) (where \(i_{1} ,j_{1}\) stand for the states of the \(I_{1}\) spin and \(i_{2} ,j_{2}\) stand for the states of the \(I_{2}\) spin), we obtain that the populations \(p_{{i_{1} i_{2} }} = \rho_{{i_{1} i_{2} ,i_{1} i_{2} }}\) and \(p_{{i_{1} j_{2} }} = \rho_{{i_{1} j_{2} ,i_{1} j_{2} }}\) are equal (there is a symmetry with respect to the state of the second nucleus). At the same time, we assume that the product states with different \(|i_{1} \rangle\) states have different populations, equal to \(p_{\alpha }\) and \(p_{\beta }\) states for \(|i_{1} \rangle = |\alpha \rangle\) and \(|i_{2} \rangle = |\beta \rangle\). Hence, in the Zeeman basis, the density matrix of the reaction product is as follows:

$$ \rho = \rho_{{I_{1} }} \otimes \rho_{{I_{2} }} = \left( {\begin{array}{*{20}c} {p_{\alpha } } & 0 \\ 0 & {p_{\beta } } \\ \end{array} } \right) \otimes \left( {\begin{array}{*{20}c} {1/2} & 0 \\ 0 & {1/2} \\ \end{array} } \right). $$
(2)

Hence, the density matrix is diagonal in the Zeeman basis of states and the populations of the resulting four-level system are

$$ p_{\alpha \alpha } = \frac{1}{2}p_{\alpha } , \quad p_{\alpha \beta } = \frac{1}{2}p_{\alpha } ,\quad p_{\beta \alpha } = \frac{1}{2}p_{\beta } , \quad p_{\beta \beta } = \frac{1}{2}p_{\beta } . $$
(3)

Subsequent spin evolution depends on the strength, \(B_{{{\text{pol}}}}\), of the magnetic field, at which polarization is prepared, and it is dictated by the Hamiltonian of the diamagnetic product:

$$ {\hat{\mathcal{H}}} = {\Omega }_{1} \hat{I}_{1z} + {\Omega }_{2} \hat{I}_{2z} + 2\pi J\left( {{\hat{\mathbf{I}}}_{1} \cdot {\hat{\mathbf{I}}}_{2} } \right). $$
(4)

Here \({\Omega }_{i} = - \gamma_{i} B_{{{\text{pol}}}} \left( {1 + \delta_{i} } \right)\) is the Zeeman interaction of the corresponding spin (determined by its gyromagnetic ratio \(\gamma_{i}\) and chemical shift \(\delta_{i}\)) and J is the scalar spin–spin interaction. The behavior of the nuclear spin system is determined by the relative values of J and \(\delta {\Omega }\): when \(\delta {\Omega } \gg 2\pi J\) the spins are weakly coupled, whereas in the opposite case, \(\delta {\Omega } \ll 2\pi J\), the spin are coupled strongly. One can switch between the two regimes by varying the external magnetic field strength, since \(\delta {\Omega }\) is directly proportional to the field, while J does not depend on the field.

The eigenstates of a weakly coupled system are the Zeeman states. This is the simplest situation: the density matrix is diagonal in the eigenstate basis and there is no coherent evolution (there is only relaxation of non-thermal polarization to equilibrium). The situation of a strongly coupled system is different, as two eigenstates are altered (the states \(|1\rangle = |\alpha \alpha \rangle = |T_{ + } \rangle\) and \(|4\rangle = |\beta \beta \rangle = |T_{ - } \rangle\) always remain the same):

$$ |2\rangle = \cos {\Theta |}\alpha \beta \rangle + \sin {\Theta |}\beta \alpha \rangle ,\quad |3\rangle = - \sin {\Theta |}\alpha \beta \rangle + \cos {\Theta |}\beta \alpha \rangle . $$
(5)

Here the “mixing angle” is defined as follows: \(\tan 2{\Theta } = \frac{2\pi J}{{\delta {\Omega }}}\). When the spins are coupled weakly, we obtain that \({\Theta } \to 0\) and the eigenstates are the Zeeman states. However, in the strong coupling case the states \(|2\rangle\) and \(|3\rangle\) are superposition of \(|\alpha \beta \rangle\) and \(|\beta \alpha \rangle\). In the ultimate case \(\delta {\Omega } \to 0,\) we obtain that \({\Theta } \to \pm \frac{\pi }{4}\) and the two superposition states are the singlet and central triplet states, defined in the standard way:

$$ |S\rangle = \frac{1}{\sqrt 2 }\left( {\left| {\alpha \beta } \right.\rangle - |\beta \alpha \rangle } \right),\quad \left| {T_{0} \rangle } \right. = \frac{1}{\sqrt 2 }\left( {\left| {\alpha \beta } \right.\rangle + |\beta \alpha \rangle } \right). $$

Hence, the eigenstates are characterized by symmetry with respect to exchanging the spins (symmetric triplet states and anti-symmetric singlet state). As a consequence of Eq. (5), the density matrix in the eigenstate basis is no longer diagonal, having the following non-zero elements:

$$ \begin{gathered} \rho_{11} = \frac{1}{2}p_{\alpha } , \quad \rho_{22} = \frac{1}{2}\cos^{2} {\Theta }p_{\alpha } + \frac{1}{2}\sin^{2} {\Theta }p_{\beta } , \hfill \\ \rho_{33} = \frac{1}{2}\sin^{2} {\Theta }p_{\alpha } + \frac{1}{2}\cos^{2} {\Theta }p_{\beta } , \quad \rho_{44} = \frac{1}{2}p_{\beta } , \hfill \\ \rho_{23} = \rho_{32} = C = \frac{1}{2}\sin 2{\Theta }\left( {p_{\alpha } - p_{\beta } } \right). \hfill \\ \end{gathered} $$
(6)

Hence, coherence between the two states is generated, which is a zero-quantum coherence. The reason is that the two bases have different symmetry; hence, if we project a diagonal density matrix in the Zeeman basis onto the new basis with different symmetry properties off-diagonal elements will appear. When \(2\pi J \gg \delta {\Omega }\) state mixing is maximal and the population difference of the \(|\alpha \beta \rangle\) and \(|\beta \alpha \rangle\) states is completely converted into coherence. Indeed, in this case, we obtain

$$ \rho_{22} = \rho_{33} = \frac{1}{2}\left( {p_{\alpha } + p_{\beta } } \right),\quad \rho_{23} = \rho_{32} = \frac{1}{2}\left( {p_{\alpha } - p_{\beta } } \right), $$
(7)

i.e., the populations of the \(|S\rangle\) and \(|T_{0} \rangle\) states are the same, and the coherence term is maximal.

Thus, using this simple example, we can demonstrate that the spin-polarized product molecule can be formed in a coherent state. This example is by no means unique or special. Generally speaking, in CIDNP different nuclei are polarized with different efficiency depending on the values of their hyperfine coupling constants in RP. When the experiment is performed at sufficiently low magnetic fields, the spin Hamiltonian of the reaction product often has different symmetry, meaning that when we write the density matrix in the eigenstate basis of \({\hat{\mathcal{H}}}\) off-diagonal elements, i.e., coherences, will emerge.

3 Detection of Spin Coherences

Although formation of coherences should be a common phenomenon in CIDNP experiments, detection of such coherences might be challenging.

First of all, coherences are strongly suppressed when the preparation time of polarization is finite. Second, as explained in the previous section, formation of coherences is usually favorable at low magnetic fields, whereas NMR detection is usually done at high fields.

Indeed, if we generate a coherence \(C_{0}\) at \(t = 0\), at time t is becomes equal to \(C \cdot {\text{e}}^{{ - i{\Omega }t}}\) with \({\Omega }\) being its evolution frequency. Assuming that reaction products are generated continuously during a time interval \(\tau_{{\text{p}}}\), we obtain the following coherence value at the end of the preparation period by summing up the evolution of coherences, which start at different instants of time:

$$ C = \frac{1}{{\tau_{{\text{p}}} }}\mathop \int \limits_{0}^{{\tau_{{\text{p}}} }} C_{0} \cdot {\text{e}}^{{ - i{\Omega }\left( {\tau_{{\text{p}}} - t} \right)}} {\text{d}}t = \frac{1}{{i{\Omega }\tau_{{\text{p}}} }}\left\{ {{\text{e}}^{{i{\Omega }\tau_{{\text{p}}} }} - 1} \right\}C_{0} . $$
(8)

When \({\Omega }\tau_{{\text{p}}} \ll 1\) (short preparation period), we obtain that \(C \approx C_{0}\); however, when \({\Omega }\tau_{{\text{p}}}\) is increased the coherence becomes smaller due to negative interference of oscillations starting at different instants of time. For instance, the real part of the coherence, \({\Re },\) is given by the sinc-function, \({\Re }\left\{ C \right\} = {\text{sinc}}\left( {{\Omega }\tau_{{\text{p}}} } \right) = \frac{1}{{{\Omega }\tau_{{\text{p}}} }}\sin \left( {{\Omega }\tau_{{\text{p}}} } \right)\), with the envelope decaying as \(\sim 1/\tau_{{\text{p}}}\) at long preparation times. For this reason, some of the coherences are very difficult to observe, as they average out during the preparation. The actual evolution frequency depends on the coherence order [24, 25], \(q_{ij}\), of the corresponding coherence term, \(\rho_{ij}\), which is defined as \(q_{ij} = \left\langle {i\left| {\hat{I}_{z} } \right|i} \right\rangle - \left\langle {j\left| {\hat{I}_{z} } \right|j} \right\rangle\) with \(\hat{I}_{z}\) being the z-projection of the total spin operator, \({\hat{\mathbf{I}}}\) (which is equal to \({\hat{\mathbf{I}}}_{1} + {\hat{\mathbf{I}}}_{2}\) in the two-spin case). For homonuclei, the value of \({\Omega }_{ij}\) is of the order of

$$ {\Omega }_{ij} \approx q_{ij} \cdot \gamma \cdot B_{{{\text{pol}}}} $$
(9)

except for the case of very low fields (where the J-coupling value is greater than or comparable to the nuclear Zeeman interaction, \(\gamma \cdot B_{{{\text{pol}}}}\)) and for ZQCs. In the latter case, \(q_{ij} = 0\) and the actual \({\Omega }_{ij}\) value is determined by \(\delta {\Omega }\) and the J-coupling value. When \(q_{ij} \ne 0\) (i.e., for all coherences except for ZQCs), the \({\Omega }_{ij}\) value is very large (unless the limit of ultralow fields is reached). Indeed, at a rather low field of, for instance, 10 mT, we obtain \({\Omega }_{ij} /2\pi \approx q_{ij} \cdot 400\) kHz. Hence, unless \(q_{ij} \ne 0\) and short preparation times are used, the coherence will be smeared out during the preparation period. For this reason, the case \(q_{ij} = 0\) is of special interest, i.e., the case where ZQCs are generated.

In the case \(q_{ij} = 0,\) there are several possible options, using ZQC generation and detection at high or low field.

The first option is to run the experiment at a constant field, inside an NMR spectrometer. To generate and detect a ZQC in such an experiment it is required that the density matrix of the product (determined by the properties of the \({\hat{\mathcal{H}}}_{{{\text{RP}}}}\)) has off-diagonal elements in the eigenstate basis of \({\hat{\mathcal{H}}}\). This is possible, for instance, at high fields in a situation where the two spins form an AB system in the reaction product. Hence, the density matrix is diagonal in the Zeeman state basis, but not in the eigenstate basis of \({\hat{\mathcal{H}}}\), and so the polarized reaction product is formed in a coherent state. The possibility of generating and detecting the ZQC between the states \(|2\rangle\) and \(|3\rangle\) has been demonstrated in an elegant experiment by the Ernst group [9]. In this experiment, a variable delay \(\tau_{{{\text{ev}}}}\) has been introduced between the light pulse (used to generate CIDNP) and a radiofrequency (rf) pulse (used to detect the Fourier NMR spectrum), see the protocol shown in Fig. 1. The spectra taken after different evolution times \(\tau_{{{\text{ev}}}}\) have different appearance, due to the different phase of the ZQC, which is given by the expression \({\text{ZQC}}\left( {\tau_{{{\text{ev}}}} } \right) = {\text{ZQC}}\left( 0 \right) \cdot {\text{e}}^{{ - i{\Omega }_{{{\text{ZQC}}}} \tau_{{{\text{ev}}}} }}\). with the frequency being equal to \({\Omega }_{{{\text{ZQC}}}} = \sqrt {\delta {\Omega }^{2} + \left( {2\pi J} \right)^{2} }\).

Fig. 1
figure 1

Generation of spin coherence in high-field hyperpolarization experiments. First, polarization is prepared by light irradiation, subsequently, ZQC evolution takes place, finally, the NMR spectrum is taken by applying a radiofrequency pulse and recording the Free Induction Decay (FID) signal (the NMR spectrum is given by the Fourier transform of the FID)

Full size image

The same protocol can be used to probe coherences in other hyperpolarization experiments as well. A representative example [26] is given by PHIP experiments using spin-locking. In this situation, a pair of protons originates from parahydrogen (pH2, the H2 molecule in the singlet nuclear spin state), which is attached to a suitable substrate. As a consequence, the two protons are created in the \(|S\rangle\) state. Typically, at high magnetic fields this is not an eigenstate of the spin system (since \(\delta {\Omega } \gg 2\pi J\)), but one can use spin-locking, i.e., apply a strong resonant rf-field, which makes \(|S\rangle\) an eigenstate and thus blocks singlet–triplet mixing. When the rf-field is turned off in a non-adiabatic fashion (meaning that the density matrix does not change during the switch of the rf-field) the density matrix in the Zeeman basis becomes

$$ \rho = |S\rangle \langle S| = |\alpha \beta \rangle \langle \alpha \beta | + |\beta \alpha \rangle \langle \beta \alpha | - |\alpha \beta \rangle \langle \beta \alpha | - |\beta \alpha \rangle \langle \alpha \beta |. $$
(10)

That is, the off diagonal matrix elements are present, which correspond to ZQC formation. In the product operator formalism [27], Eq. (10) can be rewritten as follows:

$$ \rho = \frac{1}{4}\hat{1} - \left( {{\hat{\mathbf{I}}}_{1} \cdot {\hat{\mathbf{I}}}_{2} } \right) = \frac{1}{4}\hat{1} - \hat{I}_{1z} \hat{I}_{2z} - {\text{ZQC}}_{x} , $$
(11)

where \(\hat{1}\) is the identity operator and the ZQC term is given by \({\text{ZQC}}_{x} = \hat{I}_{1x} \hat{I}_{2x} + \hat{I}_{1y} \hat{I}_{2y}\). Using the protocol shown in Fig. 1, one will obtain different spectra at different \(\tau_{{{\text{ev}}}}\) values. When \(\tau_{{{\text{ev}}}} = 0\), the spectrum is zero, as the singlet state is NMR silent (it does not give rise to any NMR signals); this also means that the signals originating from the \(\hat{I}_{1z} \hat{I}_{2z}\) term and from \({\text{ZQC}}_{x}\) cancel each other. In the course of free evolution, \(\hat{I}_{1z} \hat{I}_{2z}\) does not change (since this term commutes with the Hamiltonian), whereas \({\text{ZQC}}_{x}\) is mixed with the following spin order [27]: \({\text{ZQC}}_{y} = \hat{I}_{1x} \hat{I}_{2y} - \hat{I}_{1y} \hat{I}_{2x}\). The evolution of this kind is driven by the \(\delta {\Omega }\) term in the Hamiltonian [27], with the evolution period of \(T = 1/\delta {\Omega }\). Similar results can be obtained using the photo-PHIP method [28, 29], which enables fast formation of two magnetically non-equivalent protons in the singlet state.

The resulting spectral pattern [26], see Fig. 2, then depends on the relative contributions of the two ZQC terms, while the \(\hat{I}_{1z} \hat{I}_{2z}\) term always gives rise to the same spectral pattern, namely, to two anti-phase doublets. When \(\tau_{{{\text{ev}}}}\) is equal to half-period of the ZQC evolution, \(T/2\), the \({\text{ZQC}}_{x}\) term changes its sign, whereas the \({\text{ZQC}}_{y}\) is zero. As a consequence, the intensity of the two anti-phase doublets is doubled, as compared to the case where only the \(\hat{I}_{1z} \hat{I}_{2z}\) term is present. When \(\tau_{{{\text{ev}}}}\) is equal to \(\left( {2n + 1} \right)T/4\) (with \(n\) being an integer number) the \({\text{ZQC}}_{x}\) contribution is absent and only the term from \({\text{ZQC}}_{y}\) stays. It is interesting to note that the NMR signals originating from different terms also have a different flip angle dependence, which is \(\sin 2\varphi\) for \(\hat{I}_{1z} \hat{I}_{2z}\) and \({\text{ZQC}}_{x}\) (signals disappear when \(\varphi = \pi /2\)) and \(\sin \varphi\) for \({\text{ZQC}}_{y}\) (maximal signal at \(\varphi = \pi /2\)). This allows one to separate the different contributions. The signals originating from \({\text{ZQC}}_{y}\) are very specific: they are maximal a for 90-degree detection pulse and they contain only dispersive components. Hence, ZQC formation gives rise to very characteristic spectral patterns.

Fig. 2
figure 2

Spectral patterns of a two-spin system originating from different spin order: \(\hat{I}_{1z} \hat{I}_{2z}\) (top), \({\text{ZQC}}_{x}\) (middle) and \({\text{ZQC}}_{y}\) (bottom). In the first two cases, the signal intensity is proportional to \(\sin 2\varphi\) and in the third case it is proportional to \(\sin \varphi\)

Full size image

A possible modification of the high-field experiment is to set \(\tau_{{{\text{ev}}}}\) equal to a constant value (e.g., set it equal to zero) but to use pulsed preparation of polarization. In the CIDNP case, this can be done using light pulses. When the inter-pulse delay is synchronized with the ZQC evolution, certain coherences can be enhanced or suppressed at will. For instance, if the pulses are repeated after half a period of the ZQC evolution, the corresponding coherence will be washed out; if the repetition time is equal to a full evolution period, they will be enhanced.

Generally speaking, formation of ZQCs in high-field experiments is relatively uncommon, because the density matrix is usually diagonal in the Zeeman state basis, which is also (in most cases) an eigenstate basis for the reaction products. As a consequence, all ZQCs become zero. Therefore, it is much more common that ZQCs are generated in low field experiments. In this situation, there are two possible options of how to detect them: detection directly at the low \(B_{{{\text{pol}}}}\) field or detection at high field. To the best of our knowledge, the first option has not been explored so far, whereas the second option can be implemented using the protocol shown in Fig. 3.

Fig. 3
figure 3

Protocol of CIDNP experiments at variable magnetic field. In step 1, polarization is formed by light irradiation of the sample at the polarization field \(B_{{{\text{pol}}}}\) during a time period of \(\tau_{{\text{p}}}\). Subsequently, free evolution of polarization is taking place in step 2 during the time period \(\tau_{{{\text{ev}}}}\). After that, field variation \(B_{{{\text{pol}}}} \to B_{0}\) is performed in step 3 and NMR spectrum at the \(B_{0}\) field is acquired in step 4

Full size image

The protocol used to detect the ZQC comprises the following steps, see Fig. 3. Polarization is generated (step 1) at \(B = B_{{{\text{pol}}}}\) during time period \(\tau_{{\text{p}}}\); then it freely evolves (step 2) during time \(\tau_{{{\text{ev}}}}\) at the same field. After that (in step 3), a non-adiabatic field jump \(B_{{{\text{pol}}}} \to B_{0}\) is introduced and the Fourier NMR spectrum is taken (in step 4). When variation of the field is non-adiabatic the ZQC can be converted into the observable polarization of the coupled spins. To demonstrate this, we consider a two-spin system at a low magnetic field (such that \(2\pi J \gg \delta {\Omega }\) and the eigenstates are singlet and triplet states) and assume that the density matrix has a coherence term:

$$ \rho = C|S\rangle \langle T_{0} | + \,C^{*} |T_{0} \rangle \langle S|. $$
(12)

If we write down the same terms in the Zeeman basis (i.e., in the high-field eigenstate basis), we obtain the expression:

$$ \rho = {\Re }\left\{ C \right\}\left. {\left| {\alpha \beta } \right.} \right\rangle \left\langle {\alpha \beta } \right.\left| { - {\Re }\left\{ C \right\}} \right|\left. {\beta \alpha } \right\rangle \left. {\left\langle {\beta \alpha } \right.} \right|. $$
(13)

If we assume that the field jump happens instantaneously, the density matrix has no time to change, but the eigenstate basis changes, i.e., the resulting density matrix is given by Eq. (13). This expression tells us that the \(S - T_{0}\) ZQC is converted into the population difference of the \(|\alpha \beta \rangle\) and \(|\beta \alpha \rangle\) states, which can be determined from the high-field NMR spectrum. Hence, the experimental protocol depicted in Fig. 3 indeed allows one to probe the ZQCs formed at a low polarization field. By repeating the experiment at variable \(\tau_{{{\text{ev}}}}\) one can probe the temporal evolution of the ZQC. Thus, ZQCs are detected indirectly at the high \(B_{0}\) field after a non-adiabatic field jump.

Nonetheless, the outlined method is challenging in many cases. The reason is that the field jump is commonly done by transporting the sample from a low polarization field into an NMR spectrometer. Implementing a non-adiabatic (ideally, instantaneous) field jump using such a method was impossible to implement for a long time: this is most likely the reason why formation of ZQCs is usually ignored. If the field switch is adiabatic, conversion of the ZQC into population difference does not occur. Despite the technical challenges, there are experimental methods, which allow one to perform a non-adiabatic field jump by fast positioning of the NMR probe [30] or the NMR sample [31] or using a pneumatic system [32]. One should note here that favorable conditions for observing ZQCs are achieved at LACs [19] when two levels, \(|i\rangle\) and \(|j\rangle\), closely approach each other and get mixed by a perturbation term. Under such conditions, the ZQC evolution frequency, \({\Omega }\), is minimal. Furthermore, in the LAC region the perturbed eigenstates, \(|i^{\prime}\rangle\) and \(|j^{\prime}\rangle\), are superposition of \(|i\rangle\) and \(|j\rangle\); hence, the ZQC between the perturbed states will be converted to the population difference of the \(|i\rangle\) and \(|j\rangle\) states by rapidly moving the spin system away from the LAC, very much in the same way as the \(S - T_{0}\) coherence is converted into the population difference of the \(|\alpha \beta \rangle\) and \(|\beta \alpha \rangle\) states.

4 Polarization Transfer

We would like to stress that the study of ZQCs in hyperpolarization experiments is not only a matter of pure curiosity, but has important practical consequences. Namely, they mediate coherent polarization transfer among strongly coupled spins. Furthermore, in many cases, ZQCs are difficult to detect (using the indirect detection method described above) but the consequences of their evolution are apparent, giving rise to observable polarization transfer.

Discussing the polarization transfer issue, we first consider CIDNP in a two-spin system with \(A_{1} \ne A_{2}\); for clarity we take \(A_{2} = 0\). In this situation, only one of the two spins is polarized directly during the RP evolution. When the density matrix of the spin pair is given by Eqs. 2 and 6, we obtain that the nuclear spin polarizations are (here \(P_{0}\) is the starting polarization of \(I_{1}\)):

$$ \left\langle {I_{1z} } \right\rangle = {\text{Tr}}\left\{ {\hat{I}_{1z} \rho } \right\} = \frac{{p_{\alpha } - p_{\beta } }}{2} = P_{0} , \quad \left\langle {I_{2z} } \right\rangle = {\text{Tr}}\left\{ {\hat{I}_{2z} \rho } \right\} = 0. $$
(14)

However, if we let the ZQC, \(\rho_{23}\), vary, the result will be different. For instance, if we set \(\rho_{23} = 0\), for instance, due to preparation during a finite period of time, we obtain (in the limiting case \({\Theta } = \pi /2\))

$$ \left\langle {I_{1z} } \right\rangle = \left\langle {I_{2z} } \right\rangle = \frac{1}{2}P_{0} . $$
(15)

That is, the polarization is evenly distributed between the two spins. If we assume that the initial value of \(\rho_{23}\) is given by Eq. 6, but let the ZQC evolve with time, the polarization values are [16, 19]

$$ \left\langle {I_{1z} } \right\rangle = \frac{1}{2}\left( {1 + \cos {\Omega }t} \right)P_{0} , \quad \left\langle {I_{2z} } \right\rangle = \frac{1}{2}\left( {1 - \cos {\Omega }t} \right)P_{0} . $$
(16)

Hence, coherent oscillations of polarization are taking place, conditioned by the ZQC evolution. In practice, it is usually difficult (although not impossible [16, 17]) to observe the evolution described by Eq. 16 and only the final values of polarization can be measured, achieved when ZQC goes to zero. Apparently, the ZQC evolution then leads to polarization transfer among strongly coupled spins, as has been shown for the first time by de Kanter and Kaptein [33]. In some cases, cross-relaxation also contributes to polarization transfer, but coherent processes, which come into play at low fields where the nuclei are strongly coupled, are usually significantly faster and more efficient. Of course, when \({\Theta } \to 0\), i.e., when the spins are coupled weakly, coherent polarization transfer phenomena are no longer manifest: as follows from Eq. (6) the spin states are populated in accordance with the singlet–triplet mixing in the RP and the coherence term is zero.

Polarization transfer phenomena are also common in PHIP experiments, involving strongly coupled spin systems. In PHIP, there are only two primarily polarized spins, namely, the two pH2-nascent protons prepared in the singlet state. A common task in PHIP experiments is to transfer the spin order of these two protons to target spins of choice, which can be other protons [34,35,36,37,38] or spin-1/2 heteronuclei [39,40,41,42,43,44,45,46,47,48,49,50], e.g., 13C, 15N, 19F, 31P, etc. PHIP transfer phenomena can be qualitatively understood using the same idea as in the case of CIDNP. When the spins are strongly coupled, the \(|S\rangle\) state of the two pH2-nascent protons does not correspond to an eigenstate of the Hamiltonian of the reaction product (except for the case where their total spin is conserved, \(\left[ {\left( {{\hat{\mathbf{I}}}_{1} + {\hat{\mathbf{I}}}_{2} } \right),{\hat{\mathcal{H}}}} \right] = 0\)). Hence, singlet-state preparation gives rise to formation of the product in a coherent spin state. Once spin coherences are formed, they start evolving giving rise to polarization transfer in a coupled spin network. In practice, it is hard to observe such coherences because PHIP relies on relatively slow reactions, i.e., the polarized reaction products are formed continuously during a certain time interval and the coherences are smeared out. Hence, an apparently “spontaneous” polarization transfer is found experimentally, although the underlying polarization transfer is usually of a coherent nature. Coherent transfer phenomena in PHIP can be revealed by modifying the experimental protocol. For instance, one can run the reaction at a high magnetic field (where the spins are coupled weakly) and then introduce a non-adiabatic jump to a low field (where the spins are coupled strongly) to generate spin coherences [37]. The evolution of such coherences can be mapped out by varying the evolution time at low field (followed by a non-adiabatic jump to the high detection field).

The magnetic field range, where coherent polarization transfer phenomena take place in PHIP experiments, can be deduced from the strong coupling condition. Indeed, when the characteristic difference in the Zeeman interactions, \(\delta {\Omega }\), is smaller than or comparable to the effective coupling strength, \(J_{{{\text{eff}}}}\), the spins are coupled strongly and coherent polarization transfer is operative. For protons \(\delta {\Omega }\sim \gamma_{{\text{H}}} \cdot B_{{{\text{pol}}}} \cdot {\Delta }_{\delta }\) (with \(\gamma_{{\text{H}}}\) being the proton gyromagnetic ratio and \({\Delta }_{\delta }\) the characteristic chemical shift difference between the pH2-nascent protons and target protons in the reaction product), whereas for heteronuclei \(\delta {\Omega }\sim \left( {\gamma_{{\text{H}}} - \gamma_{{\text{X}}} } \right) \cdot B_{{{\text{pol}}}}\) (with \(\gamma_{{\text{X}}}\) being the gyromagnetic ration of the X-nucleus). Using typical NMR parameters we can conclude that polarization transfer among protons is efficient at mT or even tesla fields, whereas for the transfer to heteronuclei much lower fields are required, which are in the µT or even nT range. This motivates running experiments at ultralow field: such polarization transfer experiments are nowadays frequently used in various applications of PHIP.

5 CIDNP Experiments on Trp–Trp Dipeptides

We want to illustrate the key concepts of this paper using as an example the Trp–Trp dipeptide polarized by CIDNP. Previously, the kinetics and mechanism of the photoinduced electron transfer from dipeptide Trp–Trp to triplet-excited 2,2′-dipyridyl (DP) were systematically studied in aqueous solutions in a wide pH range at high magnetic field by time-resolved CIDNP techniques [51]. The peculiarity of this photoinduced reaction was the following: despite the high reactivity of tryptophan a threshold effect of protonation of the terminal amino group of the dipeptide on the quenching of the triplet-excited state of 2,2′-dipyridyl was revealed. At a pH of aqueous solutions lower than the pKa2 (pH < 7.6) of the terminal amino group of the dipeptide, the reversible electron transfer involves only the C-terminal residue of the dipeptide (Trp2):

figure a

It was also established that no intramolecular electron transfer occurs from the tryptophan residue at the N-end to the tryptophan radical (Trp1) to the oxidized residue at the C-end (Trp2). At a pH of the aqueous solutions higher than the pKa2 of the terminal amino group of the dipeptide, both tryptophan residues equally participate in the triplet-excited dipyridyl quenching [51]. As we show below, in the Trp–Trp dipeptide polarization transfer is possible within various coupled spin subsystems and also between such subsystems, notably, between different residues. A more detailed study can reveal the coherent nature of polarization transfer and the role of LACs therein. The structure of the molecule and the polarization transfer pathways discussed in this work are shown in Scheme 1.

Scheme 1
scheme 1

Structure of Trp–Trp with primarily polarized protons highlighted and polarization transfer pathways. Here Trp1 and Trp2 denote the two residues of Trp–Trp, namely, Trp1 is the N-terminal residue and Trp2 is the C-terminal residue. Red and blue colours indicate the protons with positive (red) and negative (blue) hyperfine interaction constants in transient radical polarization in the Trp2 residue; they acquire polarization directly in the radical pair. Green color highlights protons of the same residue participating in the coherent polarization transfer via direct coupling to the primarily polarized protons. Magenta color shows long-range polarization transfer to the protons of the residue Trp1

Full size image

5.1 Sample Preparation, Reaction Conditions

l-Trp–l-Trp (> 99%) was purchased from Bachem, 2,2′-dipyridyl-d8 (> 99%), deuterated water D2O (> 99.9%), DCl, NaOD were purchased from Sigma-Aldrich. The measurements were carried out in deuterated water. The required pH values were achieved by adding small amounts of DCl and NaOD solution. The reagent concentrations were 3.0 mM Trp–Trp, 7.8 mM 2,2'-dipyridyl-d8 at pH = 6.55. Before each measurement, the samples were purged with pure nitrogen gas for 10 min to remove dissolved oxygen, a step necessary to ensure that dipyridyl triplets generated by laser light react mostly with Trp–Trp dipeptide molecules.

5.2 Field-Cycling CIDNP Experiments

The experiments were carried out using a setup allowing fast field-cycling NMR experiments with CIDNP hyperpolarization. This setup has been described in detail in Ref. [52]. Two series of experiments were carried out: measurements of the CIDNP field dependences and experiments with variable evolution time after the sample irradiation, thus aimed at studying the kinetics of polarization transfer in the Trp–Trp peptide.

To measure the CIDNP field dependence we used the protocol shown in Fig. 3. The sample, placed in the NMR probe, was kept at the position of lowest field of the NMR shuttle for 2 min to suppress thermal polarization. Then the sample with the probe was transferred to the variable polarization field \(B_{{{\text{pol}}}}\), where it was irradiated by XeCl excimer laser pulses for 0.5 s with a pulse frequency of 50 Hz, an energy of 120–125 mJ per pulse, λ = 308 nm, for generating CIDNP. After that, the sample was transferred to the observation field \(B_{0} = 7\) T, where the NMR signal was measured using a 45° radiofrequency pulse.

In the second series of experiments, the evolution time \(\tau_{{{\text{ev}}}}\) after the irradiation of the sample was varied (see Fig. 3). As in the first series of experiments, the thermal polarization was suppressed by waiting at the lowest position of the NMR shuttle for two minutes. Then the sample was transferred to the desired field \(B_{{{\text{pol}}}}\), where it was irradiated by XeCl excimer laser pulses for 0.1 s. Then, after an evolution period of a duration \(\tau_{{{\text{ev}}}}\), the sample was transferred to the observation field \(B_{0} = 7\) T, where the NMR signal was recorded using a 45° radiofrequency pulse.

5.3 Experimental Results

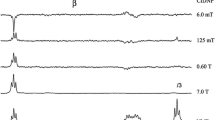
CIDNP spectra of Trp–Trp obtained for different polarization fields are shown in Fig. 4. It is useful to point out that the CIDNP pattern acquired at high polarization field reflects, which spins are primarily polarized in the course of the RP spin evolution. Indeed, at high field spins are coupled weakly and coherent polarization exchange is inefficient. Hence, from the CIDNP spectrum corresponding to \(B_{{{\text{pol}}}} = B_{0} = 7\;{\text{T}}\) we conclude that only the protons of the C terminus of Trp–Trp are polarized directly, specifically, the aromatic protons in the H2, H4 and H6 positions (denoted as H2-Trp2, H4-Trp2 and H6-Trp2, respectively) and also the β-CH2 protons of residue Trp2 of the dipeptide, labeled β1-Trp2 and β2-Trp2. Hereafter, we denote the N-terminus of the dipeptide as Trp1 and the C-terminus as Trp2. Hence, in the photoreaction with the dye dipyridyl-d8 the radical center in the dipeptide Trp–Trp of the spin-correlated RP is formed exclusively at the C-terminal residue.

Fig. 4
figure 4

Top spectrum: 300 MHz 1H NMR spectrum of 3 mM Trp–Trp and 2,2′-dipyridyl-d8 in D2O at pH = 6.55 at thermal equilibrium. Below we show CIDNP spectra of the same sample recorded for different polarization fields, \(B_{{{\text{pol}}}}\), which are indicated. The CIDNP spectra were taken without time delay after the irradiation by laser pulses for 0.5 s. The asterisk marks impurities in the solvent. Signal assignment is given on the plot. Color coding is implemented to distinguish primarily polarized protons from protons that acquired polarization due to polarization transfer: red and blue colours indicate the protons with positive (red) and negative (blue) hyperfine interaction constants in transient radicals in residue Trp2. Green color highlights protons of the Trp2 residue participating in the coherent polarization via direct coupling to the primarily polarized protons. Magenta color shows long-range polarization transfer to the H2-Trp1 (at 5.4 mT) and α-Trp1 (at 1 mT) protons of the residue Trp1. For better visibility, the aromatic parts of CIDNP spectra at 0.05, 0.2, 0.46, and 1.2 T are multiplied by a factor of 5, the aromatic part of the CIDNP spectrum at 5.4 mT was divided by a factor of 2, the aliphatic parts of the CIDNP spectra at 5.4, 0.1 and 1 mT are divided by factors of 3, 1.5, and 1.5, respectively

Full size image

At low \(B_{{{\text{pol}}}}\) fields, the situation is qualitatively different due to strong coupling between different spin networks. At fields below 1 T polarization is transferred from the β-CH2 protons to the α-CH proton of the C terminus and also among the aromatic protons, giving rise to CIDNP signals of the H5-Trp2 and H7-Trp2 protons. As a consequence, the signals of α-Trp2, H5-Trp2 and H7-Trp2 are enhanced, although direct polarization of these nuclei by CIDNP is tiny (due to the tiny hyperfine coupling of the electron spin with these nuclei in the RP). Moreover, at low magnetic fields (below 10 mT) CIDNP signals can be found even for the N-terminal Trp residue, namely, for the H2-Trp1 proton (see Fig. 4); that is, polarization transfer is possible even among different residues once the strong coupling condition is fulfilled. Hence, indirect polarization of nuclear spins via coherent polarization transfer is efficient in this case.

In the case under study, it is also instructive to show the magnetic field dependence of polarization. Here we present it for the proton in α-Trp2 position, see Fig. 5. One can see that polarization transfer is indeed taking place only at low fields, where the α-Trp2 proton is strongly coupled to the β1-Trp2 and β2-Trp2 protons. In addition to this, in the field dependence there is a spike-like feature at 0.32 T, which is due to the LAC in the coupled three-spin system consisting of the α-Trp2, β1-Trp2 and β2-Trp2 protons. A similar feature has been reported in CIDNP studies of spin systems of the same kind [17, 53, 54]. This sharp feature as well as the broad maximum at about 0.1 T should not be attributed to any peculiarities of the spin dynamics in the RP: they are entirely due to the spin dynamics in the reaction product, i.e., due to coherent CINDP transfer.

Fig. 5
figure 5

Magnetic field dependence of CIDNP of the α-Trp2 proton of Trp–Trp

Full size image

The fact that the feature at \(B_{{{\text{LAC}}}} = 0.32\) T is due to a LAC gives the opportunity to demonstrate the coherent nature of polarization transfer: as mentioned above, the ZQC evolution frequency is minimal at LACs. To reveal the coherent behavior of polarization exchange we utilized the same experimental protocol, see Fig. 1, and used a short \(\tau_{{\text{p}}}\) time (to make sure that the relevant ZQCs are not washed out) and a variable \(\tau_{{{\text{ev}}}}\) time at a fixed polarization field \(B_{{{\text{pol}}}} = B_{{{\text{LAC}}}}\). The measured \(\tau_{{{\text{ev}}}}\) dependences of CIDNP of the relavant signals (polarization of the α-Trp2, β1-Trp2 and β2-Trp2 protons) are shown in Fig. 6. In the time dependence, one can clearly see oscillations. Although the oscillations are damped by spin relaxation, at least one period of oscillations is distinctly visible. The ZQC oscillation frequency, which is about 1 Hz, corresponds to the splitting of the two levels, which have the LAC [17, 53, 54].

Fig. 6
figure 6

CIDNP dependence on the evolution time \(\tau_{{{\text{ev}}}}\) at the LAC field \(B_{{{\text{LAC}}}} = 0.32\) T measured for the α-Trp2 and β-Trp2 protons of Trp–Trp

Full size image

Coherent evolution of CIDNP is by no means limited to the three-spin system considered above. In Trp–Trp, pronounced oscillations of polarization can be found for other protons as well, namely for the aromatic protons of C-terminal Trp. This is illustrated in Fig. 7. In this example, coherent polarization exchange is taking place between the H4-Trp2 and H7-Trp2 protons (primarily, the H4-Trp2 proton is polarized, but not the H7-Trp2 proton): the \(\tau_{{{\text{ev}}}}\) dependence of CIDNP contains a pronounced oscillatory component. It is noteworthy, that direct coupling between these protons is small, less than 1 Hz. Nonetheless, polarization exchange between them is possible and it occurs with a frequency of about \(\nu_{{{\text{ZQC}}}} \approx 4\) Hz, which is considerably greater than the direct coupling between the H4-Trp2 and H7-Trp2 protons. The reason for this is that the four aromatic protons—H4-Trp2, H5-Trp2, H6-Trp2 and H7-Trp2—form a strongly coupled network, with each spin being strongly coupled to its direct neighbors. In such a system, cross-talk among all coupled spins becomes possible [16, 53, 55].

Fig. 7
figure 7

CIDNP dependence on the evolution time \(\tau_{{{\text{ev}}}}\) at \(B_{{{\text{pol}}}} = 1\) mT measured for the H4-Trp2 and H7-Trp2 protons of Trp–Trp. Solid lines describe the best fit with the function \(M_{i} = A_{i} {\text{e}}^{{ - \frac{{\tau_{ev} }}{{T_{1} }}}} \left( {1 + B_{i} \sin \left[ {2\pi \nu_{{{\text{ZQC}}}} + \phi_{i} } \right]\tau_{{{\text{ev}}}} } \right) + C_{i}\)

Full size image

Polarization transfer is also possible between the two residues of Trp–Trp. However, the transfer process is slow, relying on the small inter-residue J-couplings, most likely, the coupling between the α-CH protons. In this case, in the polarization time trace (not shown here) there are no clear oscillations, as relaxation kicks in. Nevertheless, polarization transfer is possible, as seen from the CIDNP spectra acquired at low \(B_{{{\text{pol}}}}\) fields, see Fig. 4.

6 Summary and Conclusions

Hence, in this paper we give clear evidence that chemical reaction products can indeed be formed in a coherent spin state. For a long time, this phenomenon was ignored, except for a few papers [9, 10]. Nonetheless, careful examination of low-field experiments shows that formation of hyperpolarized molecules in a coherent state is a ubiquitous phenomenon in CIDNP. Here we explain under what conditions such coherences can be generated and how they can be probed experimentally. Furthermore, we stress that such coherences play the key role in polarization transfer allowing one to transfer CIDNP from primarily polarized spins to other nuclei in a molecule under study. Particularly strong effects of this kind are commonly observed at LACs [19]. The relevance of polarization transfer in strongly coupled spin systems goes beyond the field of CIDNP: such polarization transfer is frequently exploited in PHIP experiments (and then it is often termed “spontaneous” polarization transfer) to polarize protons and heteronuclei.