Abstract
A large variety of the samples of novel magnetic materials, which are of high interest due to their exotic properties, are only available in very small sizes. In some cases, it is not possible to synthesize large single crystals; in other cases, the small size itself is the key prerequisite to manifest a specifically interesting property of the material. The smallness of a sample rises a problem of the detection of the static magnetic response and of the electron spin resonance (ESR) signal. To overcome this problem, we propose to use a cantilever-based (torque-detected) setup with the capability of a simultaneous measurement of ESR and static magnetization. This setup offers a high sensitivity and the ability to acquire along with the ESR signal the components of the magnetization tensor in a single experimental run. Here, we present the working principle of this setup, as well as the estimate of its sensitivity from the measurements on the standard Co Tutton salt sample.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Torque magnetometry (TM) is a rapidly developing field in experimental magnetism, which, due to an increased sensitivity of various torque sensors, provides valuable insights into the fundamental properties of magnetic materials [1]. It has been successfully used for studies of molecular magnets [2, 3], low-dimensional antiferromagnets [4], and nanoparticles [5], just to name a few. Moreover, due to a steadily increasing quality of the torque sensors new methods have been developed, pushing further investigations in this field [6,7,8,9]. The torque-detected electron spin resonance (TD-ESR) has also been used by a few groups worldwide, and has proven to be a powerful technique to study magnetic properties of various compounds, especially when the conventional means of the ESR detection are not sensitive enough. Z. Zhang et al. showed a ferromagnetic resonance (FMR) measurement on a microcrystal of yttrium iron garnet performed in small magnetic fields [10]. E. Ohmichi and H. Ohta with colleagues demonstrated the measurements extended to strong static and pulsed magnetic fields and the sub-THz microwave range [11,12,13]. F. E. Hallak et al. performed high-frequency ESR measurements on molecular magnets using the copper beryllium alloy capacitive cantilevers [14, 15]. The authors of the present paper showed the applicability of the torque detection technique to FMR studies of thin ferromagnetic films [16] and of layered van der Waals materials [17]. In addition, it is important to mention the magnetic resonance force magnetometry technique which demonstrated the outstanding results in the detection of spatially resolved ESR on microscopic samples [18,19,20].
In the present paper, we report the realization of a combined TM and TD-ESR techniques in a single device which, besides providing a high sensitivity, enables a simultaneous acquisition of the ESR signal and the longitudinal and transversal components of the static magnetization of the studied material in the same experimental run. The working principle of this device, operational at high microwave frequencies, high magnetic fields and low temperatures, is presented here together with the estimates of the sensitivity of the torque-detected magnetometry and ESR, respectively. More generally, the described setup can also be used for the detection of FMR and antiferromagnetic resonance in the magneticaly ordered materials.
2 Description of the setup
Before describing the implementation of TD-ESR technique it is important to consider the static torque magnetometry first. TM measures the mechanical torque acting on a magnetic sample in a homogeneous magnetic field \(\mathbf {H}\) due to the non-collinearity between \(\mathbf {H}\) and the magnetization \(\mathbf {M}\), which arises due to the presence of the transverse magnetization \(M_{\mathrm{T}}\), i.e., the magnetization component perpendicular to the external magnetic field. For any magnetic material the appearance of \(M_{\mathrm{T}}\) is a consequence of magnetic anisotropy. In a TM experiment the sample is glued to a microcantilever (Figs. 1a and 2). In the low magnetic field limit, the finite \(M_{\mathrm{T}}\) gives rise to a static cantilever bending [1], whereas the other, longitudinal component of magnetization \(M_{\mathrm{L}}\) yields a shift of the cantilever eigenfrequency \(\varDelta \nu _{\mathrm{C}}\) [6]. At any applied magnetic field the complete magnetization tensor can be calculated from the measured angular dependences of the torque and of the eigenfrequency shift by solving the equation of motion of the cantilever, as is shown, e.g., in Refs. [1, 5, 6, 21].
The effect of the resonant absorption of the microwave (MW) radiation by a magnetic sample attached to a cantilever can be understood both from the quantum mechanical and classical points of view. In the former, it changes the population of the spin levels split by the Zeeman effect with respect to the equilibrium Boltzmann distribution in a way which depends on the transition probabilities, on the MW power, and on the spin-lattice relaxation time. In the latter, it changes the spatial direction of the magnetization with respect to magnetic field and crystallographic axes of the sample. As a result, the resonance absorption leads to a change in the torque signal—affecting both the eigenfrequency and dynamical bending, i.e., the vibration amplitude—which can be used to detect magnetic resonance transitions. A detailed mathematical description of the resonance absorption detected by a cantilever can be found, e.g., in the review by E. Ohmichi et al. [13].
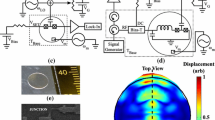
The principle scheme for a high-sensitive detection of the TM and TD-ESR signals is shown in Fig. 1b. It implements a simultaneous measurement of the cantilever bending, eigenfrequency and vibration amplitude as will be explained below. The microcantilevers (Fig. 1a) were manufactured by SCL-Sensor.Tech. Fabrication GmbH (see also Ref. [22]). The key elements of the setup, the instrumentation amplifier, phase shifter and automatic gain circuit (AGC) were homemade. The frequency counter, DC voltmeter and lock-in amplifier are commercially available devices from Keysight, Keitley and Stanford Research Systems, respectively. The amplitude modulated microwave source was produced by Virginia Diodes, Inc., and the superconducting magneto-optical cryostat for the generation of magnetic field equipped with a \(^4\)He variable-temperature inset (VTI) was made by Oxford Instruments. The microcantilever with the sample attached (Fig. 2) was placed inside the VTI on a sample holder. The MW radiation was guided to the sample through the cryostat windows by optical means using focusing polypropylene lenses. The sample holder can be rotated in the VTI to change the angle between the sample axes and the direction of the magnetic field.
As can be seen in Fig. 1a, the microcantilever has four piezo sensors (\(\textit{R}_{1,2,3,4}\)) arranged in the Wheatstone bridge [22]. Two of them are in the bending part and the other two are in the body of the cantilever. Application of a constant voltage to two poles of this bridge produces a DC voltage across the bridge if the cantilever is bent and an AC voltage if the cantilever is vibrating. There are several methods of modulation of the cantilever’s vibration amplitude. At the tip of the cantilever there is a structure (heater) to which one can apply a DC or AC current. Such current induces a magnetic moment of the heater structure perpendicular to the cantilever. In the DC mode it will result in a bending of the cantilever in an external magnetic field, whereas in the AC mode it will induce its vibration. Another options are the use of a piezo-shaker, or the amplitude modulation of the MW radiation, as described below. All these options are available in the present setup.
As shown in Fig. 1b, the amplitude-modulated MW source emits radiation, which is focused using lenses on the cantilever with the sample attached to it. If the modulation frequency of the microwave matches the eigenfrequency of the cantilever, then due to the mechanical resonance its vibration amplitude drastically increases. This vibration is picked up with piezo-resistors and transformed into an AC voltage across the Wheatstone bridge. This voltage is then amplified with the instrumentation amplifier and sent to four devices (see Fig. 1b). The DC voltmeter measures a constant component of the voltage, which is proportional to the static bending of the cantilever. The frequency counter measures the cantilever oscillation frequency (eigenfrequency). The signal is also sent directly to the lock-in amplifier to measure the vibration amplitude. Part of the signal is branched off to the phase shifter and the AGC connected to the reference input of the lock-in amplifier. The phase shifter provides matching the phase for stable oscillation and the AGC [23] keeps a constant level of the signal sent to the reference channel. Further, the reference output of the lock-in amplifier is connected to the modulation input of the MW source, which makes this circuit self-excited, i.e., the reference frequency always follows the eigenfrequency of the cantilever enabling a precise measurement of the latter and enhancing the overall sensitivity.
3 Test results
TD-ESR and static TM results obtained on the CTS test sample at \(T = 7\) K. Vibration amplitude (a) and the shift of the eigenfrequency \(\varDelta \nu _{\mathrm{C}}/(\mu _0 H)^2\) (b) of the cantilever as a function of magnetic field. In the left, the color coding shows the angles between the sample and magnetic field. c \(M_{\mathrm{L}}/(\mu _0 H)\) and \(M_{\mathrm{T}}/(\mu _0 H)\) as a function of angle between the sample and magnetic field at \(\mu _{0}H = 1\) T
For the calibration of the above described setup a standard sample of the cobalt Tutton salt (CTS) Co(NH\(_{\text {4}}\))\(_{\text {2}}\)(SO\(_{\text {4}}\))\(_{\text {2}}\) \(\cdot \)6H\(_{\text {2}}\)O was used. This magnetically anisotropic compound was investigated before with the TD-ESR technique in Ref. [24]. In our measurements, a microcrystal of CTS was placed at the tip of the cantilever, as shown in Fig. 2. The mass of this sample was \(\approx 0.5\) \( \upmu \)g corresponding to \(N_\mathrm{{spins}} \approx 7 \cdot 10^{14}\) Co spins \(S = 1/2\) in the sample volume. The vibration amplitude of the microcantilever with the sample measured as a function of magnetic field at a MW frequency \(\nu _{\mathrm{MW}} = 120\) GHz and at a temperature \(T = 7\) K for different directions of the applied magnetic field is shown in Fig. 3a. Note, that the spectra are shifted vertically for a better presentation of the systematic shift of the resonance fields. Here two well-defined ESR lines (A and B) are clearly visible. They show an angular dependence which is expected for this material, as documented in Ref. [24]. Both lines are also present in the magnetic field dependence of the shift of the cantilever eigenfrequency. Its is shown in Fig. 3b as \(\varDelta \nu _{\mathrm{C}}/(\mu _{0}H)^2\) vs. H for clarity. Here the data is plotted as measured, i.e. without any vertical shift, in contrast to Fig. 3a. Since the eigenfrequency and the static bending amplitude of the cantilever are determined by the longitudinal and transversal components of the static magnetization tensor \(\mathbf {M} = [M_{\mathrm{L}},\, M_{\mathrm{T}}]\), these measurements provide simultaneously the field and the angular dependence of \(M_{\mathrm{L}}\) and \(M_{\mathrm{T}}\). For instance, collection of the values of \(\varDelta \nu _{\mathrm{C}}/(\mu _{0}H)^2\) at the magnetic field of \(\mu _{0}H = 1\) T and at every angle (triangles in Fig. 3b) enables plotting \(M_{\mathrm{L}}/\mu _{0} H\) as a function of angle (Fig. 3(c), triangles). The same procedure applied to the measurements of the cantilever bending (not shown) yields an angular dependence of \(M_{\mathrm{T}}/\mu _{0} H\) at \(\mu _{0}H = 1\) T (Fig. 3c, circles). Note, that the torque signal, and therefore the sensitivity, strongly depend on the direction of the external magnetic field, since all torque components vanish if the field lies along a principal magnetic direction [15, 25]. However, in the present setup with a simultaneous detection of the static bending, the eigenfrequency and of the vibration amplitude, when the measured torque is zero, the eigenfrequency shift is maximum, thereby allowing to perform the measurements at any direction of the magnetic field with respect to the sample without significant loss of the sensitivity.
Admittedly, the sensitivity of such TD setup is quite difficult to estimate, because it depends on many parameters including the applied magnetic field, MW power, the magnitude of the magnetic anisotropy of the studied material, the spring constant of the cantilever, and the sensitivity of the piezoresistors. However, basing on the test measurements of CTS, we can estimate the sensitivity for this particular compound on the cantilever with the spring constant value of 17.1 N/m, which was used in these measurements. This can be done by calculating a signal-to-noise ratio (\(SNR_{TM}\)) for the frequency shift and static bending. The division of the number of spins by \(SNR_{TM}\) yields an estimate for the sensitivity \(SN_{TM} = N_\mathrm{{spins}}/SNR_{TM}\) for the particular measurement. The result is that for the torque magnetometry at \(\mu _{0}H = 1\) T and \(T = 7\) K the minimum number of \(1.5\cdot 10^{13}\) Co spins (\(\sim 10^{-7}\) emu) and \(3\cdot 10^{12}\) Co spins (\(\sim 3\cdot 10^{-8}\) emu) can be detected in the measurement of the static bending amplitude and frequency shift, respectively. These values compare to the ultimate sensitivity of a standard SQUID magnetometer with a vibration sample magnetometry (VSM) option [26], which can be achieved by using the signal averaging technique during a considerable amount of time. The practical sensitivity of a SQUID magnetometer without the VSM option is one or even two orders of magnitude lower. Moreover, the SQUID sensitivity drops with increasing magnetic field, whereas the torque sensor sensitivity increases. It is important to mention, that in the case of our TM setup the measurements were performed without any signal-to-noise ratio improvement technique. A respective improvement of the setup planned for future should further increase its sensitivity far beyond the capability of a SQUID magnetometer. Furthermore, unlike a standard SQUID magnetometer, the TD setup can measure simultaneously two orthogonal components of the magnetization tensor \(\mathbf {M} = [M_{\mathrm{L}},\, M_{\mathrm{T}}]\).
The sensitivity of the TD-ESR detection is estimated similar to the torque magnetometry, but with taking into account the ESR linewidth (LW): \(SN_\mathrm{{ESR}} = N_\mathrm{{spins}}/(SNR \cdot LW)\). \(SNR_\mathrm{{ESR}}\) is given by the ratio of the ESR signal amplitude and the noise level. \(SN_\mathrm{{ESR}}\) amounts to \(2\cdot 10^{8}\) spins/G and \(9\cdot 10^{9}\) spins/G, for the measurement of the vibration amplitude and the frequency shift, respectively. Here only in the measurement of the vibration amplitude the lock-in technique was used to improve the signal-to-noise ratio, which results in a better sensitivity value. These numbers surpass by few orders of magnitude the sensitivity of a commercial X-band spectrometer amounting typically to \(10^{11} - 10^{12}\) spin/G [27], and are about 5 times better than the sensitivity reported for the previous TD-ESR measurements of the same CTS compound [11, 12].
4 Conclusions
The torque detected ESR and magnetometry setup presented here appears to be a very sensitive tool to study magnetic properties of the micrometer size samples with by orders of magnitude better sensitivity as compared to a standard ESR spectrometer and a SQUID magnetometer. The ability to measure the resonance absorption of the microwaves simultaneously with two perpendicular components of the static magnetization enhances the sensitivity and increases the quality of the acquired data, because the experimental conditions are identical for the TD-ESR and TM measurements. In addition, this also reduces the time needed for the measurements. Still, there is a sizable room for the improvement of the sensitivity of the setup. Implementation of the averaging techniques, the use of more powerful MW sources, cantilevers with a lower spring constant etc., can boost the performance of this setup, which likely will enable measurements of the samples with even smaller number of spins. At present the described setup is capable to perform measurements on rather anisotropic magnetic materials. If a sample is magnetically isotropic, the magnetization will follow the direction of the magnetic field without exerting any torque on the cantilever. However, it is possible to perform torque measurements also in materials without anisotropy. To measure such samples it will be necessary to create a magnetic field gradient at the sample, which will generate a force at the sample and pull the cantilever, as, e.g., demonstrated in Refs. [7, 13]. Such upgrade of the setup is planned as well.
References
M. Perfetti, Cantilever torque magnetometry on coordination compounds: from theory to experiments. Coord. Chem. Rev. 348, 171 (2017). https://doi.org/10.1016/j.ccr.2017.08.013
A. Cornia, M. Affronte, A.G. Jansen, D. Gatteschi, A. Caneschi, R. Sessoli, Magnetic anisotropy of Mn\(_{12}\)-acetate nanomagnets from high-field torque magnetometry. Chem. Phys. Lett. 322, 477 (2000). https://doi.org/10.1016/S0009-2614(00)00464-4
M. Perfetti, E. Lucaccini, L. Sorace, J.P. Costes, R. Sessoli, Determination of magnetic anisotropy in the lntrensal complexes (ln = tb, dy, er) by torque magnetometry. Inorg. Chem. 54(7), 3090 (2015). https://doi.org/10.1021/acs.inorgchem.5b00288
A. Zorko, M. Herak, M. Gomilšek, J. van Tol, M. Velázquez, P. Khuntia, F. Bert, P. Mendels, Symmetry reduction in the quantum kagome antiferromagnet herbertsmithite. Phys. Rev. Lett. 118, 017202 (2017). https://doi.org/10.1103/PhysRevLett.118.017202
J. Körner, C.F. Reiche, R. Ghunaim, R. Fuge, S. Hampel, B. Büchner, T. Mühl, Magnetic properties of individual Co\(_2\)FeGa Heusler nanoparticles studied at room temperature by a highly sensitive co-resonant cantilever sensor. Sci. Rep. 7(1), 8881 (2017). https://doi.org/10.1038/s41598-017-08340-z
B. Gross, D.P. Weber, D. Rüffer, A. Buchter, F. Heimbach, A. Fontcuberta i Morral, D. Grundler, M. Poggio, Dynamic cantilever magnetometry of individual CoFeB nanotubes. Phys. Rev. B 93, 064409 (2016). https://doi.org/10.1103/PhysRevB.93.064409
H. Takahashi, T. Okamoto, E. Ohmichi, H. Ohta, Wide-dynamic-range cantilever magnetometry using a fiber-optic interferometer and its application to high-frequency electron spin resonance spectroscopy. Appl. Phys. Express 9(12), 126701 (2016)
M. Wu, N.L.Y. Wu, T. Firdous, F. Fani Sani, J.E. Losby, M.R. Freeman, P.E. Barclay, Nanocavity optomechanical torque magnetometry and radiofrequency susceptometry. Nat. Nanotechnol. 12, 127 (2017). https://doi.org/10.1038/nnano.2016.226
F. Arnold, M. Naumann, T. Lühmann, A.P. Mackenzie, E. Hassinger, Application of squids to low temperature and high magnetic field measurements–ultra low noise torque magnetometry. Rev. Sci. Instrum. 89(2), 023901 (2018). https://doi.org/10.1063/1.5011655
Z. Zhang, P.C. Hammel, P.E. Wigen, Observation of ferromagnetic resonance in a microscopic sample using magnetic resonance force microscopy. Appl. Phys. Lett. 68, 2005 (1996). https://doi.org/10.1063/1.115619
H. Ohta, E. Ohmichi, Recent advances in high-frequency electron spin resonance detection using a microcantilever. Appl. Magn. Reson. 37, 881 (2010). https://doi.org/10.1007/s00723-009-0067-6
H. Takahashi, E. Ohmichi, H. Ohta, Mechanical detection of electron spin resonance beyond 1 THz. Appl. Phys. Lett. 107, 182405 (2015). https://doi.org/10.1063/1.4935204
E. Ohmichi, T. Okamoto, H. Takahashi, H. Ohta, Mechanically detected terahertz electron spin resonance. Appl. Magn. Reson. (2020). https://doi.org/10.1007/s00723-020-01279-x
F.E. Hallak, J. van Slageren, M. Dressel, Torque detected broad band electron spin resonance. Rev. Sci. Instrum. 81, 095105 (2010). https://doi.org/10.1063/1.3482158
F.E. Hallak, P. Neugebauer, A.L. Barra, J. van Slageren, M. Dressel, A. Cornia, Torque-detected ESR of a tetrairon(III) single molecule magnet. J. Magn. Res. 223, 55 (2012). https://doi.org/10.1016/j.jmr.2012.08.008
A. Alfonsov, E. Ohmichi, P. Leksin, A. Omar, H. Wang, S. Wurmehl, F. Yang, H. Ohta, Cantilever detected ferromagnetic resonance in thin Fe\(_{50}\)Ni\(_{50}\), Co\(_{2}\)FeAl\(_{0.5}\)Si\(_{0.5}\) and Sr\(_{2}\)FeMoO\(_{6}\) films using a double modulation technique. J. Magn. Reson. 270, 183 (2016). https://doi.org/10.1016/j.jmr.2016.07.011
J. Zeisner, A. Alfonsov, S. Selter, S. Aswartham, M.P. Ghimire, M. Richter, J. van den Brink, B. Büchner, V. Kataev, Magnetic anisotropy and spin-polarized two-dimensional electron gas in the van der Waals ferromagnet Cr2Ge2Te6. Phys. Rev. B 99, 165109 (2019). https://doi.org/10.1103/PhysRevB.99.165109
Z. Zhang, M.L. Roukes, P.C. Hammel, Sensitivity and spatial resolution for electron-spin-resonance detection by magnetic resonance force microscopy. J. Appl. Phys. 80(12), 6931 (1996). https://doi.org/10.1063/1.363767
D. Rugar, R. Budakian, H.J. Mamin, B.W. Chui, Single spin detection by magnetic resonance force microscopy. Nature 430, 329 (2004). https://doi.org/10.1038/nature02658
I. Lee, Y. Obukhov, G. Xiang, A. Hauser, F. Yang, P. Banerjee, D.V. Pelekhov, P.C. Hammel, Nanoscale scanning probe ferromagnetic resonance imaging using localized modes. Nature 466, 845 (2010). https://doi.org/10.1038/nature09279
D.P. Weber, D. Rüffer, A. Buchter, F. Xue, E. Russo-Averchi, R. Huber, P. Berberich, J. Arbiol, A. Fontcuberta i Morral, D. Grundler, M. Poggio, Cantilever magnetometry of individual Ni nanotubes. Nano Lett. 12(12), 6139 (2012). https://doi.org/10.1021/nl302950u
M. Dukic, J.D. Adams, G.E. Fantner, Piezoresistive AFM cantilevers surpassing standard optical beam deflection in low noise topography imaging. Sci. Rep. 5, 16393 (2015). https://doi.org/10.1038/srep16393
F.J. Giessibl, High-speed force sensor for force microscopy and profilometry utilizing a quartz tuning fork. Appl. Phys. Lett. 73, 3956 (1998). https://doi.org/10.1063/1.122948
E. Ohmichi, S. Hirano, H. Ohta, Design of in situ sample rotation mechanism for angle-dependent study of cantilever-detected high-frequency ESR. J. Magn. Reson. 227, 9 (2013). https://doi.org/10.1016/j.jmr.2012.11.018
A. Cornia, D. Gatteschi, R. Sessoli, New experimental techniques for magnetic anisotropy in molecular materials. Coord. Chem. Rev. 219–221, 573 (2001). https://doi.org/10.1016/S0010-8545(01)00352-6
R.L. Fagaly, Superconducting quantum interference device instruments and applications. Rev. Sci. Instrum. 77(10), 101101 (2006). https://doi.org/10.1063/1.2354545
J. Möser, K. Lips, M. Tseytlin, G. Eaton, S. Eaton, A. Schnegg, Using rapid-scan epr to improve the detection limit of quantitative epr by more than one order of magnitude. J. Magn. Reson. 281, 17 (2017). https://doi.org/10.1016/j.jmr.2017.04.003
Acknowledgements
This article is dedicated to the great ESR scientists Klaus Möbius and Kev Salikhov on the occasion of their \(85^{\mathrm{th}}\) birthdays. AA is thankful for numerous discussions of the principles of TD-ESR with E. Ohmichi and H. Ohta. This work was financially supported by the Deutsche Forschungsgemeinschaft (DFG) through grant No. AL1771/4-1 and grant No. KA1694/12-1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alfonsov, A., Büchner, B. & Kataev, V. All-on-Chip Concurrent Measurements of the Static Magnetization and of the Electron Spin Resonance with Microcantilevers. Appl Magn Reson 53, 555–563 (2022). https://doi.org/10.1007/s00723-021-01339-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00723-021-01339-w