Free Induction Decay in Zigzag Spin Chains in a Multi-pulse NMR Experiment

Abstract

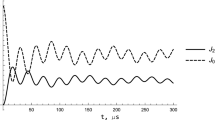
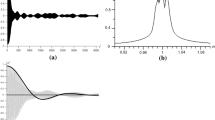
The free induction decay (FID) is investigated for zigzag (alternating) spin chains in the approximation of the nearest neighbor interactions. The dependence of the FID on the ratio of dipolar coupling constants (the parameter of dimerization) is also studied. Possible comparison of the obtained results with the experimental data for proton zigzag chains in a single crystal of hambergite is discussed.

Appendix

The long-time asymptotic behavior of the FID of Eq. (18)

We rewrite $G(D_1t)$ of Eq. (18) as follows:

$$\begin{aligned} G(D_1t)\approx \frac{1}{\pi }\int \limits _{-\alpha }^{\pi -\alpha } \mathrm{d}x\,\cos [D_1t\sqrt{1+ 2\delta \cos (2x)+\delta ^2}],\quad \delta >1. \end{aligned}$$

(21)

The extremal points of the radical in (21) are:

$$\begin{aligned} x_1=0,\qquad x_2=\frac{\pi }{2}. \end{aligned}$$

(22)

Expanding the expression under the radical in Taylor series in the vicinity of $x_1=0$, one can obtain:

$$\begin{aligned} \sqrt{\delta ^2+2\delta \cos (2x)+1}\approx \delta +1-\frac{2\delta x^2}{\delta +1}. \end{aligned}$$

(23)

Analogously, in the vicinity of $x_2=\pi /2$ ($x=\pi /2+y$), one finds:

$$\begin{aligned} \sqrt{\delta ^2+2\delta \cos 2(\frac{\pi }{2}+y)+1}\approx \delta -1 +\frac{2\delta y^2}{\delta -1}. \end{aligned}$$

(24)

Since the main contributions to $G(D_1t)$ are due to the vicinity of the extrema, one can write:

$$\begin{aligned} G(D_1 t)\approx & {} \frac{1}{\pi }\int \limits _{-\epsilon }^\epsilon \mathrm{d}x\, \cos \left\{ D_1t\left( \delta +1-\frac{2\delta x^2}{\delta +1}\right) \right\} \nonumber \\&\quad +\frac{1}{\pi }\int \limits _{\frac{\pi }{2}-\epsilon }^{\frac{\pi }{2}+\epsilon } \mathrm{d}y\, \cos \left\{ D_1 t \left[ \delta - 1 +\frac{2\delta y^2}{\delta +1}\right] \right\} \nonumber \\= & {} \frac{1}{\pi }\int \limits _{-\epsilon }^\epsilon \mathrm{d}x\, \left\{ \cos \left[ D_1 t\left( \delta +1-\frac{2\delta x^2}{\delta +1}\right) \right] \right. \nonumber \\&\quad +\cos \left. \left[ D_1 t\left( \delta -1 +\frac{2\delta y^2}{\delta +1}\right) \right] \right\} \nonumber \\= & {} \frac{1}{\pi }\sqrt{\frac{\delta +1}{2\delta D_1t}}\int \limits _{-\epsilon }^\epsilon \mathrm{d}z\, \cos \left[ (\delta +1) D_1 t -z^2\right] \nonumber \\&\quad +\frac{1}{\pi }\sqrt{\frac{\delta -1}{2\delta D_1 t}}\int \limits _{-\epsilon }^\epsilon \mathrm{d}z\, \cos \left[ (\delta -1)D_1 t +z^2\right] . \end{aligned}$$

(25)

Since the main contribution to the integrals of Eq. (25) comes from the vicinity of $z=0$, it is legitimate to set the integration limits to infinity. Using the value of the Fresnel integrals [29]:

$$\begin{aligned} \int \limits _{-\infty }^\infty \cos (z^2)\, \mathrm{d}z=\int \limits _{-\infty }^\infty \sin (z^2) \mathrm{d}z=\sqrt{\frac{\pi }{2}}, \end{aligned}$$

(26)

one can obtain from Eq. (25):

$$\begin{aligned}&G(D_1 t) =\nonumber \\&\quad \frac{1}{2\sqrt{\pi \delta D_1 t}}\left\{ \sqrt{\delta +1} \cos \left[ (\delta +1) D_1 t\right] +\sqrt{\delta -1} \cos \left[ (\delta -1) D_1 t\right] \right\} \nonumber \\&\quad +\frac{1}{2\sqrt{\pi \delta D_1 t}} \left\{ \sqrt{\delta +1} \sin \left[ (\delta +1)D_1t\right] -\sqrt{\delta -1}\sin \left[ (\delta -1) D_1 t\right] \right\} . \end{aligned}$$

(27)

Equation (27) can be rewritten as follows:

$$\begin{aligned} G(D_1t)=\nonumber \\ \frac{\sqrt{\delta +1}}{2\sqrt{\pi \delta D_1 t}}\left\{ \cos \left[ (\delta +1)D_1 t\right] + \cos \left[ \frac{\pi }{2} -(\delta +1)D_1 t\right] \right\} \nonumber \\ +\frac{\sqrt{\delta -1}}{2\sqrt{\pi \delta D_1 t}}\left\{ \cos \left[ (\delta -1)D_1 t\right] -\cos \left[ \frac{\pi }{2} - (\delta -1) D_1 t\right] \right\} . \end{aligned}$$

(28)

After simple trigonometric transformations in Eq. (28), one obtains finally:

$$\begin{aligned} \begin{aligned} G(D_1t)\approx (2\pi \delta D_1 t)^{-1/2} \left\{ \sqrt{\delta +1} \cos \left[ (\delta +1)D_1 t-\frac{\pi }{ 4 }\right] +\right. \\ \left. \sqrt{\delta -1}\cos \left[ (\delta -1)D_1t+\frac{\pi }{4}\right] \right\} . \end{aligned} \end{aligned}$$

(29)

Formula (29) coincides with Eq. (20).