Insights into the Spin–Orbital Entanglement in Complex Iridium Oxides from High-Field ESR Spectroscopy

Abstract

Complex iridium oxides have attracted recently a substantial interdisciplinary attention due to an intimate entanglement of spin and orbital degrees of freedom which may give rise to a novel spin–orbital Mott insulating behavior and exotic quantum spin liquid phases. Electron spin resonance (ESR) spectroscopy is known to be an instructive tool for studying the spin–orbital coupling (SOC) effects as it can directly access the relevant parameters sensitive to SOC, such as the g factor tensor, magnetic anisotropy gaps and spin dynamics. In this article, a systematic study at the Leibniz IFW Dresden of the static and dynamic properties of selected Ir-based materials with multi-frequency high-field ESR spectroscopy will be reviewed. Specifically, evidence for a surprisingly isotropic antiferromagnetic spin dynamics and the inversion of the orbital states in the prototypical spin–orbital Mott insulator $\text {Sr}_2\text {IrO}_4$, observation of the collective resonance modes in the family of double perovskites $\text {La}_2$ B $\text {IrO}_6$ (B = Cu, Co) and the origin of the unexpected magnetism in the double perovskite $\text {Ba}_2\text {YIrO}_6$ will be highlighted.

1 Introduction

A large interest in complex iridium oxides was triggered by the theoretical predictions of unconventional electronic and magnetic properties of these compounds including the spin–orbital Mott-insulating behavior which can evolve into superconductivity upon charge carriers’ doping, magnetic frustration and spin liquid behavior [1,2,3,4,5]. As compared to the widely studied 3d-transition metal oxides, such as the superconducting cuprates and manganites with colossal magnetoresistance, the boosted strength of the spin–orbit coupling (SOC) in the 5d-iridates and a notably larger spatial extension of the 5d orbitals equalize the energy scales of the electron–electron Coulomb interaction, the width of the electronic bands and of the SOC. Essentially this equalization, which is in the stark contrast with the clear separation of these energy scales in the cuprates, forms the basis of the new physics in the iridates.

In the majority of the studied so far compounds, Ir ions occur in the 4+ oxidation state with 5 electrons on the $t_{2\mathrm g}$ orbitals of the 5d shell with one unpaired spin $S = 1/2$. The strong SOC couples it with the remaining orbital momentum $l = 1$ of the 3-fold degenerate $t_{2\mathrm g}$ orbital set yielding a strongly anisotropic Karmers doublet characterized by the SOC entangled effective spin $j_{\text {eff}}=1/2$ [6]. Theoretical models treating the Ir-based spin lattices of various topology predict exotic magnetic properties arising from the complex nature of the $j_{\text {eff}}=1/2$ states [7, 8]. The list of the most prominent compounds comprises the layered perovskites $\text {Sr}_2\text {IrO}_4$ [9] and $\text {Sr}_3\text {Ir}_2\text {O}_7$ [10], compounds with the honeycomb structural moieties ${\text {Na}}_{2}{\text {IrO}}_{3}$ [11], $\alpha$-$\text {Li}_2\text {IrO}_3$ [12] and their three-dimensional counterparts $\beta$- and $\gamma$-$\text {Li}_2\text {IrO}_3$ [13,14,15], and the hyperkagome compound ${\mathrm {Na}}_{4}{\mathrm {Ir}}_{3}{\mathrm {O}}_{8}$ [16]. Another important case of the iridates is compounds with the double perovskite crystallographic structure $\text {La}_2$ B $\text {IrO}_6$. Here, the $B^{2+}$ site can be occupied with a paramagnetic 3d ion, such as $\text {Mn}^{2+}$, $\text {Fe}^{2+}$, $\text {Co}^{2+}$, $\text {Ni}^{2+}$, $\text {Cu}^{2+}$, or with the nonmagnetic $\text {Mg}^{2+}$ or $\text {Zn}^{2+}$ ions [17,18,19,20].

ESR spectroscopy is known to be an instructive tool for studying the SOC-related effects as it can directly access the relevant parameters sensitive to spin–orbital coupling, such as the g factor tensors, magnetic anisotropy gaps and spin dynamics. However, ESR studies of strongly correlated transition metal oxides are very challenging because magnetic interactions between the spins in these materials are by orders of magnitude larger than in chemical and biological substances and strongly anisotropic, which enormously broaden the ESR signals, besides the resonance excitations are often strongly gapped. Fortunately, as it is evidently documented in this special issue of Applied Magnetic Resonance, recent instrumentation advancements have expanded the frequency window of ESR towards the THz region and opened new frontiers to explore the physics of novel materials with strong correlations between spin, charge and orbital degrees of freedom.

In the Leibniz Institute for Solid State and Materials Research IFW Dresden, we have built up a flexible set of apparatuses for high-field multi-frequency ESR spectroscopy. For the frequency generation and detection, we employ two high-frequency network analyzers (PNA-X from Keysight Technologies and MVNA from AB Millimetre), an amplifier/multiplier chain (AMC from Virginia Diodes Inc.), and a hot electron InSb bolometer (QMC Instruments). With these instruments, a frequency range from 0.02 to almost 1 THz can be covered. For the generation of magnetic fields up to 16 T we use a high-homogeneity superconducting magnet system from Oxford Instruments equipped with a variable temperature insert operational in a temperature range 1.8–300 K. The broad-band probe heads are constructed for ESR measurements in the reflection and transmission modes in the Faraday configuration, i.e., the propagation vector of the microwaves is kept parallel to the direction of the static magnetic field. These ESR instruments enabled us to obtain interesting insights into the magnetic properties of several selected iridium based compounds, as will be detailed in the next sections.

2 Low-Energy Magnetic Exitations and Inversion of the Orbital States in the Intrinsically Stacked Oxide $\text {Sr}_\mathbf{2}\text {IrO}_\mathbf{4}$ [21, 22]

$\text {Sr}_2\text {IrO}_4$ was proposed as a first realization of the SOC-assisted Mott insulator [9]. The strong SOC gives rise to a narrow half-filled band due to the overlap of the $j_{\text {eff}}=1/2$ orbital states, which splits by the relatively small on-site Coulomb repulsion energy of electrons $U \sim 0.5$ eV into a fully occupied lower Hubbard band and an empty upper Hubbard band. The layered perovskite structure of $\text {Sr}_2\text {IrO}_4$, the Mott insulating state and the occurrence of the antiferromagnetic (AFM) order at $T_{\mathrm{N}} \approx 240$ K [23] trace intriguing similarities with the celebrated cuprate $\text {La}_2\text {CuO}_4$, the parent compound of high temperature superconductors, and raised hope to make this iridate conducting and even superconducting upon doping. However, considering the strongly anisotropic nature of the $j_{\text {eff}}=1/2$ moments, one expected substantial differences in the magnon excitation spectrum as compared to the excitations of the AFM ordered almost isotropic $S = 1/2$ $\text {Cu}^{2+}$ moments in $\text {La}_2\text {CuO}_4$ [24]. Inelastic neutron scattering, which can probe such excitations and examine their q-momentum dependence, is very difficult in the iridates due to a strong absorption of neutrons by the Ir atom and the small size of the crystals, while other spectroscopic methods, such as inelastic X-ray scattering, do not have sufficient energy resolution. In this situation, high-frequency ESR spectroscopy, albeit being restricted to the uniform $q = 0$ excitations, can be very helpful because of its high sensitivity and an excellent energy resolution down to $\sim 1$ $\upmu$eV.

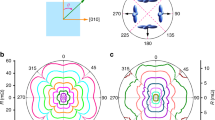
With this motivation, we measured AFM resonance (AFMR) modes in $\text {Sr}_2\text {IrO}_4$ at $T<T_{\mathrm{N}}$ at frequencies up to 500 GHz on high-quality single crystals thoroughly characterized in Ref. [23]. Typical AFMR spectra at $T = 180$ K $<T_{\text {N}}$ for the direction of the applied magnetic field ${\mathbf {H}}$ parallel to the planes of corner-sharing $\text {SrO}_6$ octahedra (${\mathbf {H}}\parallel [110]$) are shown in Fig. 1. The signal exhibits a steep up-field shift of the resonance field $H_{\text {res}}$ with increasing the frequency $\nu$. The approximation of the $\nu$ vs. $H_{\text {res}}$ to $H = 0$ reveals a zero-field excitation gap $\varDelta \approx 150$ GHz (Fig. 1a). Upon lowering the temperature, the signal broadens and acquires a structure presumably due to an inhomogeneous distribution of the internal field [25], while the zero-field gap increases up to $\varDelta \approx 200$ GHz. Turning the field direction normal to the $\text {SrO}_2$ planes (${\mathbf {H}}\parallel [001]$) makes the spectra substantially broader and the $\nu$ vs. $H_{\text {res}}$ dependence much more shallow (Fig. 2). Still, its approximation to $H = 0$ yields the same zero-field gap $\varDelta \approx 200$ GHz as for the ${\mathbf {H}}\parallel [110]$ field geometry.

Fig. 1

High-frequency AFMR mode in $\text {Sr}_2\text {IrO}_4$ for the in-plane orientation of the magnetic field. Upper panel: Characteristic frequency dependence at $T = 180$ K. The $\nu (H)$ AFMR resonance branch shown in the inset reveals a gap $\varDelta \approx 150$ GHz. Bottom panel: Selected spectra at several temperatures for a fixed frequency $\nu = 474$ GHz. Dashed lines are the Lorentzian fits. (reproduced from Ref. [21])

The $\nu$ vs. $H_{\text {res}}$ diagram of the AFMR modes in $\text {Sr}_2\text {IrO}_4$ can be rationalized in the framework of the linear spin-wave theory based on the effective Hamiltonian proposed for $\text {Sr}_2\text {IrO}_4$ in Ref. [6]:

$$\begin{aligned} {{\mathcal {H}}}_{ij}=J\widetilde{\mathbf {S_i}}\cdot \widetilde{\mathbf {S_{j}}}+\varGamma \widetilde{S_{i}^{z}}\widetilde{S_{j}^{z}} +D{\big (}\widetilde{S_i^x}\widetilde{S_j^y}-\widetilde{S_i^y}\widetilde{S_j^x}{\big )}. \end{aligned}$$

(1)

Here, $\widetilde{\mathbf {S_i}}$ and $\widetilde{\mathbf {S_{j}}}$ are the pseudospin operators ($j_{\text {eff}}=1/2$). The three terms of Eq. (1) correspond to the isotropic, symmetric anisotropic and antisymmetric Dzyaloshinskii–Moriya (DM) exchange interactions characterized by the coupling constants J, $\varGamma$ and D, respectively. The anisotropic terms in Eq. (1) arise because of the staggered rotation of the $\text {IrO}_6$ octahedra in the $\text {IrO}_2$ plane which results in noncollinearity of the spin sublattices as a direct consequence of the strong SOC [23]. Solving Eq. (1) yields the following AFM modes [21, 22]:

$$\begin{aligned} h\nu _{c}=\sqrt{32{{\tilde{J}}}{{\tilde{\varGamma }}}{\widetilde{S}}^2 +(g_c\mu _\mathrm{B}H)^2/(1-{{\tilde{\varGamma }}}/2{\tilde{J}})} \end{aligned}$$

(2)

for ${\mathbf {H}}\parallel [001]\parallel c$ axis, and

$$\begin{aligned} h\nu _{ab}\approx \sqrt{32{{\tilde{J}}}{{\tilde{\varGamma }}}{\widetilde{S}}^2 +4(2{{\tilde{J}}}+{{\tilde{\varGamma }}})M_{\mathrm{FM}}H} \end{aligned}$$

(3)

for ${\mathbf {H}}\parallel [110]\parallel ab$ plane, respectively. Here, the coupling constants J, $\varGamma$ and D defined in Eq. (1) are rearranged into ${{\tilde{J}}}=\sqrt{J^2+D^2}$ and ${{\tilde{\varGamma }}}={{\tilde{J}}}-J-\varGamma >0$ to parameterize effective isotropic exchange and easy-plane anisotropy, respectively.

Fig. 2

$\nu (H)$ diagram of the AFMR excitations in $\text {Sr}_2\text {IrO}_4$ at $T = 4$ K together with characteristic spectra for two directions of the magnetic field [symbols: experimental data points, solid lines: result of the modeling according to Eqs. (2) and (3)]. Thick dashed lines show the corresponding FMR modes. The symbol ($\star$) represents the FMR mode at 9.5 GHz for $\mathbf{H}\parallel [110]$. (reproduced from Ref. [21])

With Eqs. (2) and (3), it is possible to reproduce well the experimentally observed AFM branches (solid lines in Fig. 2). Note that the field dependence of the in-plane $\nu _{\text {ab}}$ mode is determined by the weak ferromagnetic DM moment $M_{\text {FM}} \approx 0.06$ $\mu _\mathrm{B}$ arising due to noncollinearity of the spin sublattices [26]. Oscillation of these moments yields an additional ferromagnetic resonance (FMR) mode for the ${\mathbf {H}} \parallel ab$ plane geometry

$$\begin{aligned} h\nu _{\text {ab}}^{\text {FM}} = {\sqrt{(g_{ab}\mu _\mathrm{B}H)^2+4(2{{\tilde{J}}}+{\tilde{\varGamma }})M_{\mathrm{FM}}H}}, \end{aligned}$$

(4)

which vanishes for ${\mathbf {H}} \parallel c$ axis, $h\nu _{\text {c}}^{\text {FM}} \rightarrow 0$, [27, 28] (dashed lines in Fig. 2).

Magnetic anisotropy gap The zero-field gap $\varDelta = {\sqrt{32{{\tilde{J}}}{{\tilde{\varGamma }}}{\widetilde{S}}^2}} \approx 200$ GHz $= 0.83$ meV appears unexpectedly small. Considering that $\varDelta$ is the measure of magnetic anisotropy of a spin lattice, which in $\text {Sr}_2\text {IrO}_4$ is expected to be significant due to the anisotropy of the SOC entangled $j_{\text {eff}}=1/2$ moments, the smallness of $\varDelta$ is surprising. In the mentioned above layered cuprate $\text {La}_2\text {CuO}_4$, which is considered as a very close realization of the isotropic Heisenberg two-dimensional spin-1/2 antiferromagnet, the gap is significantly larger, amounting to $\sim 5$ meV [29]. To reconcile this apparent discrepancy, one can conjecture that a delicate competition between two anisotopic contributions to magnetic exchange in Eq. (1) takes place in $\text {Sr}_2\text {IrO}_4$. The antisymmetric DM interaction stabilizes the canted in-plane spin structure whereas the symmetric anisotropic exchange favors the collinear out-of-plane spin configuration. Fine tuning of the parameters enables a near compensation of the two contributions [6] resulting in an almost isotropic AFM dynamics of $j_{\text {eff}}=1/2$ effective spins in $\text {Sr}_2\text {IrO}_4$. This is consistent with a practically isotropic Heisenberg-like dynamic correlations observed in $\text {Sr}_2\text {IrO}_4$ at $T > T_{\text {N}}$ by resonant magnetic X-ray scattering [26], in a close analogy with the behavior of $\text {La}_2\text {CuO}_4$ [24]. In the scenario of a near compensation of two types of anisotropy one would expect strong pressure dependent effects since both contributions are sensitive to the rotation of the $\text {IrO}_6$ octahedra [6]. Pressure studies of magnetic anisotropy in $\text {Sr}_2\text {IrO}_4$ are, therefore, appealing.

Anisotropy of the g factor A linear increase of $\nu _{\text {c}}$ vs. H at fields larger than 5–6 T (Fig. 2) enables to estimate, with the aid of Eq. (2), the c axis g factor $g_{\text {c}} \approx 2.45$. A deviation of $g_{\text {c}}$ from the pure spin-only value of 2 is due to a uniaxial distortion of the $\text {IrO}_6$ octahedra. It generates low symmetry, noncubic crystal fields that split the threefold degenerate $t_{\text {2g}}$ orbital set of the $\text {Ir}^{4+}$ ion. Such splitting makes the g factor anisotropic with the components [30]:

$$\begin{aligned} g_{\text {c}} = (2+2k)\cos ^2\!\alpha -2\sin ^2\!\alpha , \end{aligned}$$

(5)

$$\begin{aligned} g_{\text {ab}} = 2\sin ^2\alpha + 2\sqrt{2}k\cos \alpha \sin \alpha . \end{aligned}$$

(6)

Here, k is the covalency reduction factor and $\alpha$ is the parameter characterizing the distortion. The latter is defined as $\alpha \!=\!(1/2)\arctan [2\sqrt{2}\lambda /(\lambda \!-\!2\delta )]$, where $\lambda$ is the SOC constant and $\delta$ is the magnitude of the $t_{\text {2g}}$ splitting. (In the case of the cubic symmetry $\delta = 0$ and $\alpha _{\text {cub}} = 35.26^\circ$). With the experimentally determined value of $g_{\text {c}}$ one can calculate with Eqs. (5) and (6) the in-plane component $g_{\text {ab}} = 1.75$, assuming $k = 1$ for simplicity. This estimate is consistent with the size of the ferromagnetic DM moment $M_{\text {FM}} = {\widetilde{S}}g_{\text {ab}}\mu _\text {B}\sin \phi \approx 0.06$ $\mu _\mathrm{B}$ [26] canted in the ab plane by an angle $\phi \sim 4^\circ$ which determines the slope of the $\nu _{\text {ab}}(H)$ branch [Eq. (3)]. Moreover, our ab initio quantum chemistry calculations of the g factor tensor on the multireference configuration-interaction (MRCI) level of theory [22] yield ${\mathbf {g}}^{\text {MRCI}} = [g_{\text {c}}, g_\text {ab}] = [2.31, 1.76]$ in agreement with the experimental one ${\mathbf {g}}^{\text {exp}} = [2.45, 1.74]$.

However, both the experimental and calculated ${\mathbf {g}}$ tensors give the apparently “wrong” sign of the anisotropy as compared to the prediction of the standard ligand-field theory [31]. In $\text {Sr}_2\text {IrO}_4$ the $\text {IrO}_6$ octahedra are elongated, which in the canonical picture would correspond to the positive splitting $\delta > 0$ of the $t_{\text {2g}}$ set, i.e., the out-of-plane xz and yz orbitals lower their energy $\epsilon _{xz,yz}$ and the in-plane xy orbital rises its energy $\epsilon _{xy}$ by the amount of $\delta$. Thus, according to Eqs. (5) and (6), the elongation should yield $g_{\text {ab}} > g_{\text {c}}$. One would need to contract the octahedra to get $g_{\text {c}} > g_{\text {ab}}$.

Our observation of $g_{\text {c}} > g_\text {ab}$ implies a counterintuitive conclusion that the order of the orbital levels is inverted in $\text {Sr}_2\text {IrO}_4$ despite an elongation of the $\text {IrO}_6$ octahedra, so that $\epsilon _{xz,yz}> \epsilon _{xy}$. Our computational results could resolve this puzzle [22]. The standard ligand-field theory considers an isolated cluster composed of a central transition-metal ion coordinated by the nearest ligands. This provides an adequate description of the orbital splitting for the 3d ions. However, we could show that an isolated cluster description may be insufficient in the case of the spatially extended 5d orbitals and longer-range crystal fields have to be considered. In this situation, the positive ionic charge is not confined inside the given $\text {IrO}_6$ octahedron but is distributed in $\text {Sr}_2\text {IrO}_4$ between neighboring $\text {Ir}^{4+}\text {O}_2$ and $\text {Sr}^{2+}$O planes stacking along the c axis, which effectively increases the positive charge in the $\text {IrO}_2$ plane. Such charge redistribution overcompensates the local tetragonal field due to the elongation of the $\text {IrO}_6$ octahedra and yields the inversion of the orbital states with respect to their normal ordering.

3 Static and Dynamic Magnetism of Ir-Based Double Perovskites $\text {La}_\mathbf{2}$ B $\text {IrO}_\mathbf{6}$ (B = Co, Cu) [32, 33]

Many representatives of the rich family of iridium oxides adopt the double perovskite structure $\text {La}_2$ B $\text {IrO}_6$ with either magnetic 3d transition metal (Mn, Fe, Co, Ni, Cu) or nonmagnetic (Mg, Zn) $B^{2+}$ cations. Their crystal structure is composed of the interpenetrating simple perovskite lattices La$B\text {O}_3$ and $\text {LaIrO}_3$. If the B ion is magnetic, a spin network of interacting 3d and 5d sublattices is realized featuring different types of magnetically ordered ground states [17,18,19,20]. Here, HF-ESR spectroscopic results of two representatives of the double perovskite family, polycrystalline $\text {La}_2\text {CuIrO}_6$ and $\text {La}_2\text {CoIrO}_6$, will be briefly reviewed (for more details see Refs. [32, 33]).

Fig. 3

Selected ESR spectra of $\text {La}_2\text {CuIrO}_6$ at different temperatures at a fixed frequency of $\nu = 32.22$ GHz (left: as measured spectra; right: after correction by the analyzer software). The spectra are shifted vertically for clarity. (reproduced from Ref. [32])

Fig. 4

Temperature dependence of the integrated intensity (a), linewidth (b), and resonance field (c) of the ESR signal of $\text {La}_2\text {CuIrO}_6$ at $\nu = 32.22$ GHz. The vertical dashed lines indicate the AFM ordering temperature $T_1 = T_{\text {N}} = 74$ K and the ordering temperature of the weak ferromagnetic DM moments $T_2 = 54$ K. (adopted from Ref. [32])

$\text {La}_2\text {CuIrO}_6$ orders below $T_1 =T_{\mathrm{N}} = 74$ K with a spin structure composed of two orthogonal antiferromagnetic (AFM) sublattices characterized by a very small canted moment that orders at $T_2 = 54$ K [32]. In $\text {La}_2\text {CoIrO}_6$, $\text {Ir}^{4+}$ pseudo-spins $j_{\text {eff}}=1/2$ couple AFM to the weak ferromagnetic (FM) moment of the canted $\text {Co}^{2+}$ sublattice which is ordered zigzag AFM (E-type) at a temperature slightly below 100 K [34, 35] ($T_{\text {N}}$ increases from 92 K for $H_0 = 0$ to 98 K for $H_0 = 7$ T [33]). In both compounds, a well-defined Lorentzian-shaped ESR line can be detected at $T \lesssim 120{-}140$ K. Its temperature evolution for $\text {La}_2\text {CuIrO}_6$ is shown in Fig. 3. The as-measured signal is distorted by the admixture of the dispersion (Fig. 3a), which is hardly avoidable in the broadband probe head with complex impedance. However, this distortion can be corrected, since the microwave network analyzer used in this experiment measures the complex sample response (the amplitude and the phase shift) which enables to rectify the absorption part of the signal (Fig. 3b). The T-dependence of the signal intensity, the linewidth and the resonance field is shown in Fig. 4. The frequency vs. magnetic field dependence of the ESR signal follows the linear function $h\nu = \varDelta + g\mu \text {B}H_0$ as exemplary shown in Fig. 5. The T dependence of the ESR energy gap $\varDelta$ and the g factor are presented in Fig. 6. The respective ESR parameters for the powder sample of $\text {La}_2\text {CoIrO}_6$ are shown in Fig. 7.

Observation of just a single ESR line despite the presence of two different spin systems indicates that in both materials the 3d and 5d spin sublattices are exchange coupled and precess coherently. Due to a large orbital contribution to the magnetic moment of $\text {Ir}^{4+}$ ions and thus a strong coupling to the crystal lattice a substantial broadening of the paramagnetic resonance line is expected, which explains the absence of the ESR response at $T \gg T_{\text {N}}$. The emergence of the reasonably narrow signal in the short-range ordered state above $T_{\text {N}}$ suggests the development of a collective resonance mode of the correlated 3d and 5d spins, i.e., the precession of the total magnetization of the coupled spin systems, which may be much less affected by the spin-phonon relaxation as compared to the paramagnetic resonance of the individual spins. The extended short-range ordered quasi-static regime above $T_{\text {N}}$ is evident by a gradual evolution of the parameters of the ESR signal (Figs. 4 and 7), in particular by an opening and a continuous increase of the excitation gap $\varDelta$. Its smallness suggests that it is not a magnetic anisotropy gap associated with the uniform oscillation of the magnetic sublattices, which should be at least of the order of some hundred GHz [21, 22, 36], but rather a small excitation gap for the precession of the uncompensated ferromagnetic DM moments present in both compounds [27, 28].

Fig. 5

Frequency $\nu$ vs. $H_0$ dependence of the ESR signal of $\text {La}_2\text {CuIrO}_6$ at $T = 6$ K (symbols) and a fit to the function $h\nu = \varDelta + g\mu \text {B}H_0$ (solid line). Representative ESR signals are shown in the insets. (reproduced from Ref. [32])

Fig. 6

a Temperature dependence of the ESR energy gap $\varDelta$ and b the g factor of $\text {La}_2\text {CuIrO}_6$ obtained from the $\nu (H_0)$ dependences. Dashed red lines are guides for the eye. Horizontal dashed line in b denotes the spin-only g factor of 2. The vertical dashed lines indicate the AFM ordering temperature $T_1 = T_{\text {N}} = 74$ K and the ordering temperature of the weak ferromagnetic DM moments $T_2 = 54$ K. (adopted from Ref. [32])

Fig. 7

Temperature dependence of the intensity (a), linewidth (b), and resonance field (c) of the ESR signal of $\text {La}_2\text {CuIrO}_6$ at $\nu = 95$ GHz, and of the excitation gap $\varDelta$ evaluated according to the function $h\nu = \varDelta + g\mu \text {B}H_0$ (d). Typical spectra at this frequency are shown in panel e. The vertical dashed line indicates the AFM ordering temperature $T_{\text {N}} = 92$ K in the limit of the zero applied field. (reproduced from Ref. [32])

Another interesting result is a continuous decrease of the g factor (Fig. 6b) derived from the frequency-dependent measurements at selected temperatures (Fig. 5). Note that the T-dependent shift of the resonance field at a given fixed frequency (Figs. 4c and 7c) is the effect of both the T-dependence of the gap and of the g factor. In $\text {La}_2\text {CuIrO}_6$, one would expect for the $\text {Cu}^{2+}$ ions in the distorted octahedral oxygen coordination an anisotropic g factor tensor with the typical values $g_\parallel = 2.15{-}2.30$ and $g_\perp = 2.01 {-} 2.1$ [30] and the powder average $g_{\text {av}} > 2$. For $\text {Ir}^{4+}$ ions in a distorted ligand coordination the variation of the g factors could be much larger: $0< g_\parallel < 2$ and $2< g_\perp < 2.73$ [see Eqs. (5) and (6), and Ref. [30]]. The value of $g_{\text {av}}$ is expected to be slightly smaller than 2. The observed crossover from $g_{\text {av}} > 2$ to $g_{\text {av}} < 2$ with decreasing the temperature (Fig. 6b) then implies that when approaching the ordering temperature $T_1$ from above, the ESR response is initially dominated by the precession of the short-range ordered Cu spins $S = 1/2$ whereas the correlations between the Ir pseudospins $j_{\text {eff}}=1/2$ and their involvement in the joint resonance signal increase by approaching the second characteristic temperature $T_2$. Indeed, the emergence at $T_2$ of a weak FM magnetization in the static measurements [32] indicates the full ordering of both magnetic subsystems with a slight spin canting giving rise to the static ferromagnetic DM moment of the coupled Cu and Ir sublattices. This regime is manifested in the saturation of the ESR intensity and a narrowing of the width of the signal (Fig. 4a, b).

The $\text {La}_2\text {CoIrO}_6$ system features a similar T-dependent crossover behavior of the g factor with $g \approx 2.02$ at $T = 143$ K reducing to $g \approx 1.96$ at $T = 2$ K. In the strongly distorted octahedral ligand coordination of the $\text {Co}^{2+}$ (3$d^7$, $S = 3/2$) ions occurring in $\text {La}_2\text {CoIrO}_6$ the g factor can be substantially anisotopic with $g_{zz} \gg g_{x} \sim g_{y} \sim 2$, while in the powder averaged ESR response the $g_{x,y}$ components would have the largest spectral weight. Similar to $\text {La}_2\text {CuIrO}_6$, the T dependence of the ESR intensity and of the linewidth in $\text {La}_2\text {CoIrO}_6$ level off at around 40 K (Fig. 7a, b). This suggests that also in $\text {La}_2\text {CoIrO}_6$ the Ir subsystem of pseudospins $j_{\text {eff}}=1/2$ remains “soft” below $T_{\text {N}} \sim 92$ K and the full order of the coupled Co and Ir sublattices is established at a significantly lower temperature. Although static magnetization measurements do not reveal a distinct second transition, as in $\text {La}_2\text {CuIrO}_6$, the $^{139}$La NMR data indicate the onset of the full ordering of both spin sublattices at $T \lesssim 50$ K [33] in agreement with the ESR data.

Observation of such a rich dynamics of the “two-component” Cu–Ir and Co–Ir double perovskite magnetic lattices highlights the complexity of the intra- and inter-sublattice magnetic interactions of the coupled 3d and 5d spin systems in this remarkable group of iridium oxides and calls for further development of theoretical concepts to explain their nontrivial magnetism.

4 Origin of Magnetic Behavior of the Pentavalent Iridate $\text {Ba}_2\text {YIrO}_6$ [37]

The specifics of the iridium element is that in compounds with other elements it can occur in different oxidation states. The most common one is $\text {Ir}^{4+}$ with the half-filled 3d shell, where the electrons occupy five of the six available states in the $t_{\text {2g}}$ orbital set characterized by the anisotropic $j_{\text {eff}}=1/2$ ground state, as discussed above. However, higher oxidation states, $\text {Ir}^{5+}$ and $\text {Ir}^{6+}$, are also possible. In particular, in the double perovskite family, the penta- and hexavalent iridates are not uncommon (see, e.g., Ref. [38]). The pentavalent Ir ion has four d-electrons with the total spin $S = 1$. The strong SOC should couple this spin to the $l = 1$ orbital momentum of the $t_{\text {2g}}$ triplet yielding the nonmagnetic $J = S - l = 0$ ground state [30, 31]. In the $\text {Ir}^{6+}$ ion, only three d-electrons are left. They occupy evenly three available orbital levels of the $t_{\text {2g}}$ set. As a result, the orbital momentum is abcent in this case. Therefore, $\text {Ir}^{6+}$ should be a spin-only $S = 3/2$ ion [30, 31].

Despite the expected nonmagnetic state of the $\text {Ir}^{4+}$ ion and, thus, the anticipated absence of any magnetic behavior in the pentavalent double perovskite iridates, two of them, $\text {Sr}_2\text {YIrO}_6$ and $\text {Ba}_2\text {YIrO}_6$ and their solid solutions, have attracted a great deal of attention in the magnetic community. This interest was triggered by controversial publications of experiments, some of them suggesting a strongly AFM behavior even with static order at low temperatures [39, 40], while other reported only weak paramagnetism [41,42,43,44,45,46]. On the theory side, these controversial observations led to various proposals invalidating the $S-l$ entanglement in the ground state of certain SOC-assisted Mott insulators, which may also be applicable to the pentavalent iridates in question [47,48,49,50,51,52].

Fig. 8

ESR spectra (field derivatives of absorption) of $\text {Ba}_2\text {YIrO}_6$ at the X-band frequency $\nu = 9.56$ GHz at three selected temperatures. The lines at $\sim 340$ and $\sim 360$ mT, and a triplet structure centered around $\sim 460$ mT are labeled as $g_{\text {left}}$, $g_{\text {mid}}$, and $g_{\text {right}}$, respectively, with the spin values assigned to each line. (reproduced from Ref. [37])

Fig. 9

Frequency $\nu$ vs resonance field $H_{\mathrm{res}}$ dependence of the peaks in the ESR spectrum of $\text {Ba}_2\text {YIrO}_6$ (data points). Solid lines are fits to the relation $h\nu = g\mu _{\mathrm{B}}\mu _0H_{\mathrm{res}}$ yielding the g factor values as indicated in the plot. The insets show spectra at two selected frequencies. The spectrum at 9.56 GHz was obtained by integration of the absorption derivative spectrum (cf. Fig. 8). Arrows in the upper inset indicate the expected positions of the satellites of the $g_{\text {right}}$ peak in the spectrum at 82.18 GHz which are resolved at 9.56 GHz (lower inset). (reproduced from Ref. [37])

Since most of the experimental works on (Ba,Sr)$_2\text {YIrO}_6$ were made using bulk magnetization and specific heat measurements, only the average magnetic moment and the average magnetic interaction strength can be estimated. In these experiments, it was not possible to conclude on the exact origin of the magnetic response. The ESR spectroscopy is beneficial in this respect because it can discriminate different spin centers contributing to the total magnetic response, measure their intrinsic spin susceptibility, assess the spin dynamics and spin-spin correlations. Therefore, to shed light on the origin of the unexpected magnetism of $\text {Ba}_2\text {YIrO}_6$, we have examined with multi-frequency ESR an array of small (sub-mm sized) single crystals of this compound put on an ESR-silent quartz substrate. These crystals were previously thoroughly characterized in Ref. [42], where an average moment per Ir site $\mu _{\text {eff}} = 0.44\mu _{\text {B}}$/Ir was determined and no indications of magnetic order at temperatures down to 0.4 K were found.

At the X-band frequency $\nu = 9.56$ GHz, a set of well defined resonances was observed (Fig. 8), which $\nu (H_{\text {res}}) = g\mu _{\mathrm{B}}\mu _0H_{\mathrm{res}}/h$ dependence was examined with the HF-ESR setup (Fig. 9). Based on these measurements, the signals can be classified in the left, middle, and high field side peaks with the g factors $g_{\text {left}}$  = 2.00, $g_{\text {mid}}$  = 1.90, and $g_{\text {right}}$  = 1.49, respectively. The first two can be obviously assigned to some $S=1/2$ spin species. The triplet structure of the $g_{\text {right}}$ ESR signal (Fig. 8 and the lower inset in Fig. 9) is typical for the $S = 3/2$ center where the satellites arise due to a small zero-filed splitting of the $(2S+1$) degenerate ground state manifold. A classical example of such kind of fine-structure split ESR lines is the ESR spectrum of $\text {Cr}^{3+}$ (3$d^3$, $S = 3/2$) ions in a predominantly octahedral ligand field [30]. In the HF-ESR spectrum of $\text {Ba}_2\text {YIrO}_6$ these satellites are hidden under the inhomogeneously broadened central line.

Fig. 10

T dependence of the inverse ESR intensity $1/I^{\mathrm{ESR}}$ of $\text {Ba}_2\text {YIrO}_6$ at $\nu = 9.56$ GHz and its comparison with the static bulk susceptibility $\chi$: a total ESR intensity (diamonds, left scale), bulk susceptibility (circles, right scale), and its Curie–Weiss fit $\chi ^{-1} = [\chi _0 + C/(T - \theta _{\mathrm{CW}})]^{-1}$ with the antiferromagnetic Curie–Weiss temperature $\theta _{\mathrm{CW}} = - 16$ K and the Curie constant $C =0.0294~\text {cm}^3$K/mol corresponding to the effective magnetic moment $\mu _{\mathrm{eff}} = 0.48\mu _{\mathrm{B}}$/Ir (solid line, right scale); b intensities of individual lines $1/I^{\mathrm{ESR}}_{\mathrm{i}}$. For better comparison, the data are scaled as indicated in the legend. (reproduced from Ref. [37])

Partial magnetic susceptibilities of these three different spin centers, as determined in the temperature dependent measurements of their respective ESR intensities $I^{\text {ESR}}_i(T)$, are shown in Fig. 10b and their sum $I^{\text {ESR}}_{\text {tot}}(T)$ is compared with the bulk susceptibility $\chi _{\text {bulk}}(T)$ in Fig. 10a. The T dependence of $I^{\text {ESR}}_{\text {tot}}$ and $\chi _{\text {bulk}}$ agree very well suggesting that ESR probes the same centers that contribute to the bulk magnetic response of $\text {Ba}_2\text {YIrO}_6$. Calibration of the ESR intensities against a standard reference sample [53, 54] made it possible to estimate the absolute concentration of the spin species from the fit to the Curie–Weiss law:

$$\begin{aligned} I^{\text {ESR}}_i(T) = C_i/(T - \theta ^i_{\mathrm{CW}}), \end{aligned}$$

(7)

$$\begin{aligned} C_i = n_ig^2_iS_i(S_i+1)\mu _{\mathrm{B}}^2/3k_{\text {B}}. \end{aligned}$$

(8)

The results of the fit are summarized in Table 1. They enable to draw several important conclusions. The total concentration of the spins $\sum _{i}n_{i}$ contributing to the bulk magnetic susceptibility and to the ESR spectrum is quite small and amounts to $\sim 4$ % per $\text {Ba}_2\text {YIrO}_6$ formula unit. The $S = 3/2$ species make the dominant contribution to the magnetic response because of the large spin value. Remarkably, these spin centers feature quite appreciable magnetic interaction, yielding a significantly large Curie–Weiss temperature $\theta _{\mathrm{CW}} \sim -10$ K. This interaction is the obvious reason for the observed deviation of $\chi _{\text {bulk}}(T)$ and $I^{\text {ESR}}_{\text {right}}(T)$ from the Curie–Weiss law at low temperatures (Fig. 10) and the broadening of the ESR lines (Fig. 11) due to the slowing down of the timescale of spin–spin interactions and the development of the quasi-static inhomogeneous internal fields in the sample [55]. Note that the high-temperature upturn of the $g_{\text {right}}$ linewidth is, in contrast, typical for a single ion with $S = 3/2$ and is related to the phonon modulation of the crystal-field potential, which enhances the spin-lattice relaxation rate with increasing the temperature [56].

Table 1 Parameters of the lines in the ESR spectrum of $\text {Ba}_2\text {YIrO}_6$: g factor, spin value S, Curie–Weiss temperature obtained from ESR intensities of individual lines $\theta _{\text {CW}}$, relative spectral weights of the signals $I^{\mathrm{ESR}}_{\mathrm{i}}$, absolute concentration of spins per unit cell $n_{\mathrm{i}}$, and the orbital reduction factor k. (reproduced from Ref. [37])

Fig. 11

T dependence of the width $\varDelta H$ of the ESR signals $g_{\text {left}}$, $g_{\text {mid}}$ and $g_{\text {right}}$ (main peak) of $\text {Ba}_2\text {YIrO}_6$ at $\nu = 9.56$ GHz. (reproduced from Ref. [37])

The most natural candidates for the $S = 3/2$ centers in the iridates are the $\text {Ir}^{6+}$ (5$d^3$) ions. Due to the absence of the orbital momentum their g factor $g^{\text {Ir(VI)}}$ is expected to be approximately isotropic and close to the spin-only value $g_{\text {s}} = 2$. The negative shift of $g^{\text {Ir(VI)}}$ from $g_{\text {s}}$ is due to the second-order SOC effect [30]:

$$\begin{aligned} g^{\text {Ir(VI)}}_{\parallel } \approx g^{\text {Ir(VI)}}_{\perp } = g_{\text {s}}- 8 k \lambda /\varDelta . \end{aligned}$$

(9)

With the SOC constant $\lambda \approx 0.5$ eV [57], the energy difference between the $t_{\text {2g}}$ and $e_{\text {g}}$ orbital states $\varDelta \approx 3.2$ eV [38], and with $g_{\text {right}}$  = 1.49, Eq. (9) yields a significantly reduced value of the covalency reduction factor $k = 0.4$, as is generally expected for 5d elements in a high oxidation state covalently bonded to the ligands (see, e.g., [58,59,60]).

As to the $S = 1/2$ ESR signal $g_{\text {mid}}$, it can be assigned to $\text {Ir}^{4+}$ (5$d^5$) ions with $j_{\text {eff}}=1/2$. When the distortion of the $\text {IrO}_6$ octahedron is small, Eqs. (5) and (6) reduce to

$$\begin{aligned} g^{\text {Ir(IV)}}_{||} \approx g^{\text {Ir(IV)}}_{\perp } \approx (g_{\mathrm{s}}+ 4k)/3. \end{aligned}$$

(10)

The value $g_{\text {mid}}$  = 1.9 corresponds then to $k = 0.93$. An increase of k as compared to the signal $g_{\text {right}}$ is expected since the lower oxidation state of $\text {Ir}^{4+}$ ion makes the Ir–O bond less covalent [38].

The smallest in intensity ESR signal $g_{\text {left}}$ has the g factor very close to 2. It can be tentatively associated with a small amount of localized unpaired electrons at the structural defects often present in oxide materials (see, e.g., [61]).

An approximately equal number of spin centers contributing to the ESR signals $g_{\text {mid}}$ and $g_{\text {right}}$ (Table 1) suggests, as a possible scenario, a partial static charge disproportionation $\text {Ir}^{5+}$  $\Rightarrow$ $\text {Ir}^{4+}$  + $\text {Ir}^{6+}$ in $\text {Ba}_2\text {YIrO}_6$. Also, oxygen excess and/or Ba deficiency may promote further $\text {Ir}^{6+}$ spin centers. Significant magnetic interactions observed between the Ir-based defect spin centers, present in a rather small concentration, are in agreement with the theoretical predictions of the long-range character of magnetic exchange in the 5d double perovskites involving several oxygen bridges and also nonmagnetic cations, such as $\text {Y}^{3+}$ [62, 63]. It is feasible, as our numerical calculations show [64], that such long-range interacting defects could form extended magnetic clusters if their concentration increases above a moderate threshold of $\sim 5{-} 8$%, explaining thus the unexpected magnetic behavior observed in some particular samples of $\text {Ba}_2\text {YIrO}_6$ and $\text {Sr}_2\text {YIrO}_6$ [39, 40]. Most importantly, our ESR results rule out the hotly debated scenario of the breakdown of the spin-orbit coupled $j_{\mathrm{eff}}$ states in the 5$d^{4}$ double perovskite iridates and the occurrence of a weak magnetic moment on every $\text {Ir}^{5+}$ (5$d^4$) site.

5 Conclusions

In summary, in this article, a systematic study with the multi-frequency high magnetic field ESR spectroscopy of the static and dynamic magnetic properties of several complex iridium oxides—representatives of the novel class of quantum magnets called spin-orbital Mott insulators—was reviewed. New interesting insights into the rich physics of these materials were obtained highlighting the importance of the spin-orbital coupling (SOC) effects for the unusual magnetic properties:

• (i) In the first prototype SOC Mott insulator, the layered $\text {Sr}_2\text {IrO}_4$, an unexpectedly isotropic AFM spin dynamics in the magnetically ordered state and a surprising inversion of the spectroscopic g factor implying an inversion of the ordering of the $\text {t}_{{2g}}$ orbital states of the $\text {Ir}^{4+}$ (5$d^5$) ions was found. This effect was confirmed and understood by ab initio quantum chemistry methods as being due to longer-range crystal field effects yielding a specific distribution of the ionic charges in the layered structure of $\text {Sr}_2\text {IrO}_4$;

• (ii) In the double perovskites of the $\text {La}_2$ B $\text {IrO}_6$ family with magnetic 3d ions $\text {Cu}^{2+}$ and $\text {Co}^{2+}$ on the B site, a complex cross-coupling between 5d and 3d spin systems exhibiting a remarkable gradual temperature evolution of the spin dynamics across the magnetic ordering temperature was observed. The detected resonance response was interpreted as a collective excitation mode of the interpenetrating and interacting 3d spin $S = 1/2$ or $S = 3/2$, and 5d pseudospin $j_{\text {eff}}=1/2$ networks;

• (iii) A hotly debated controversy on the unexpected magnetic behavior of the pentavalent double perovskite iridate $\text {Ba}_2\text {YIrO}_6$ was ultimately resolved. The obtained spectroscopic data evidence that the magnetism of this material is solely due to a few percent of $\text {Ir}^{4+}$ (5$d^{5}$) and $\text {Ir}^{6+}$ (5$d^{3}$) magnetic defects while the regular $\text {Ir}^{5+}$ (5$d^{4}$) sites remain nonmagnetic. These findings highlight the relevance of the long-range magnetic interactions in 5d double perovskites proposed in recent theoretical models, which might be even responsible for the magnetic order of the defect Ir-based spin centers in $\text {Ba}_2\text {YIrO}_6$ if their concentration exceeds a certain threshold value.