1 Introductive Remarks

Fe in quartz can occur in a variety of structural settings and chemical environments, being either interstitial or straight replacing Si in its tetrahedral site. According to Rossman [1], up to 6 sites have been commonly identified in the literature. Among them, two are interstitial (the so-called I-sites) and four substitutional (S-sites). The main difference among interstitial and substitutional Fe(III) resides in the fact that in the former case Fe(III) is an extra-framework ion, carrying 3 extra charges to the crystal, and thus the I site is coupled to other types of defects (even to other Fe defect sites [1]). When Fe(III) replaces Si(IV) in the tetrahedral site, a charge defect is added to the system. While being still possible that the Fe(III) impurity defect is associated to other relatively distant defects, the most frequent situation described for the charge compensation is the coupled replacement of Si(IV) by Fe(III) plus an extra monovalent ion. This latter ion could be hosted in the continuous channels crossing the crystal structure from side to side along the crystallographic c axis. Accordingly, the ion should be preferably small, suggesting a marked preference for Li+ (S1 site), H+ (S2 site) and Na+ (S3 site). Most of this coupled Fe(III):M+ centres were described in specific EPR spectroscopic studies devoted to the characterisation of a single centre on synthetic crystals [2,3,4,5,6,7,8].

The different natural quartz varieties (e.g. citrine, amethyst, green, smoky, white, ametrin, … [1]) exhibit complicated combinations of Fe defects, which, at least in some cases, are linked to the chromatic appearance of the crystals. Moreover, the defect nature of the replacement implies that spectroscopic changes can be found also in different crystals of a single variety, as a result of different chemical fingerprint or even of the thermodynamics and kinetics during the crystallisation process. All these considerations suggest that the identification of the main Fe(III) centre in natural quartz varieties could be highly challenging. Few studies have been thus carried out straight on natural amethyst samples, to assess the most frequent Fe(III) defect, and to define its structural details. Among them, one can cite [5], where the S2 site was characterised by means of the study of the superhyperfine (SHF) interaction of Fe(III) with proton nuclei in a natural amethyst sample. In 2010, a spectroscopic XAS study on Fe(III) in amethyst [9] revealed the prevailing presence of the Fe(III):H+ pair replacing for Si(IV), and providing a link to the origin of the purple colour of the crystals. The aim of the present study is to define the details of the interaction between Fe(III) and H+ in the defect centre, so as to get a detailed localisation of the proton in the structure. The study is pursued by the combined use of continuous wave and pulse EPR spectroscopy. The authors aim to emphasize that a detailed determination of the relative localisation of the proton and the metal paramagnetic ion is possible only by means of the study of the Electron Spin Echo Envelope Modulation.

2 Experimental Strategy of the Paramagnetic Resonance Measurements

Extensive continuous wave EPR (cwEPR) characterisations of Fe-bearing quartz single crystals, where the presence of the S2 centre has been assessed, are reported in [5], for natural samples, and in [2, 4] for synthetic samples. Remarkably, these studies enlighted the occurrence of two S2 centres, one more abundant (the so-called S2(D), with the proton connected to the distant oxygen) than the other (the S2(C) centre, with the proton linked to the close oxygen). In those studies, similar sets of Hamiltonian parameters were proposed, including a modest to negligible Zeeman anisotropy and a very strong Zero-Field-Splitting interaction. [4] and [5] refined the component of the SHF tensor. [2, 4] obtained a best fit also including higher-order terms in the ZFS interaction, whereas [5] excluded this necessity. One relevant aspect is that [4, 5] and [2] found all tensors (Zeeman, SHF, ZFS) partially misaligned with respect to the crystallographic reference frame. In a study by [10], carried out on the so-called S0 defect, i.e. the [FeO4/h]0 centre, while accounting for the former studies on synthetic samples, and for the spectroscopic results therein included, a simplified Hamiltonian operator was used to interpret a continuous wave single-crystal EPR spectrum of a natural amethyst. In this approach, only a fully isotropic Zeeman contribution and a strong rhombic ZFS interaction were included. Moreover, the main axes of the EPR framework were chosen coincident to that of the crystallographic framework (namely, the z direction coincident with the c axis, and the y direction aligned along the a1 axis). Following the indications by [9], we decided to perform the pulse EPR study on a single crystal of natural amethyst so that the magnetic field direction resulted perpendicular to the c axis, and to refer to the continuous wave EPR measurements to get the orientation in the x–y plane.

3 Experimental Details

A single crystal of a quartz amethyst, belonging to the same geode from which the crystals used in the work [9] were taken, was used in this study. The single crystal was cut to fit within a 3 mm internal diameter EPR tube. The c axis of the crystallographic framework, identified by the presence of the rhombohedral surfaces in the crystal morphology, was aligned along the direction of elongation of the EPR tube. Once inserted in the resonant cavity, the crystallographic framework is oriented having c perpendicular to the direction of the magnetic field. Error in the positioning on the theta angle could be of the order of one degree.

A reference cw EPR spectrum was registered at 35 K using a Bruker ELEXYS X-band EPR, equipped with an Oxford CF935 cryostat and a dielectric cavity with high Quality (Q) factor, available at the Department of Chemical Sciences of the University of Padua. The cw-EPR measurements were carried out in a cryostat, setting the temperature at 35 K. Spectra were registered at 9.68 GHz in the magnetic field range 80–720 mT, with 0.05 mT modulation amplitude and 100 kHz modulation frequency. Nominal resolution and scan speed were set to 0.16 mT and 1.9 mT s−1, respectively. Simulations of the experimental spectrum were carried out with the SIM software package [11]. The program proceeds through numerical diagonalization of the full spin Hamiltonian matrix, the retrieval of the transition fields, probabilities and intensities. The simulations were performed under a trial and error procedure.

Pulsed measurements were carried out on the same instrumentation Bruker ELEXYS without moving again the crystal, at the same temperature (35 K) and at an operating frequency of 9.676 GHz. The Echo-EPR spectrum was registered after a two-pulse (2P) π/2–τ–π–τ sequence (Table 1). Magnetic field was varied in the range 150–250 mT. Time-domain ESE spectra were registered after both the same 2P sequence used for the EchoEPR spectroscopy and after a three-pulse (3P) π/2–τ–π/2–T–π/2–τ sequence (Table 1), setting the magnetic field at the value corresponding to the maximum intensity of the Echo-EPR spectrum, i.e. 186.8 mT (vide infra). Experimental time domain was in the range 0–4092 ns for the 2P experiment and in the range 0–7152 ns for the 3P experiment, with a time step of 4 ns for both the experiments. Electron Spin Echo Envelope Modulation (ESEEM) patterns were extracted by subtracting a decay function obtained by refining a biexponential model, the form of which was y = ΣiAie−C(i)x. The software Microcal Origin 9.0 was used to perform the non-linear fit, according to a Levenberg Marquardt strategy. The resulting ESEEM patterns were Fourier transformed, after Hanning windowing and zero-filling the raw ESEEM data.

Table 1 details of the pulse sequences used in the different pulsed experiments
Full size table

4 Results

4.1 cwEPR

The experimental cw EPR spectrum of the amethyst sample is shown in Fig. 1a. Apparently, a wide number of lines, most of which characterised by a very small width (less than 1 mT, in average) are present. The evidence of lines at very high and very low effective g values are in full agreement with previous experimental studies on synthetic and natural iron-bearing quartz samples, and attributed to Fe(III) ions undergoing an intense crystal field interaction [2, 4, 5, 10]. The so large number of lines can be attributed to the occurrence of different Fe centres in the crystal and to the presence of inequivalent sites in the structure for most of them [1, 2, 4, 5, 10]. It is interesting that in the Zeeman field regions identified in [10] (i.e. at about 180, 340 and 700 mT), some lines are markedly more intense than others. We tentatively attributed these lines to the Fe(III):H+ centre, and computed the experimental spectrum using the following spin Hamiltonian, as proposed by these authors:

$$H = g\beta \hat{B}\hat{S} + \hat{S}D\hat{S}$$
Fig. 1
figure 1

experimental cw EPR (a), computed cw EPR (b) and EchoEPR (c) spectra of the natural amethyst crystal registered at 35 K. Magnetic field values are expressed in milliTesla (mT)

Full size image

The best fit (simulation) (Fig. 1b) has been achieved with D = − 10.1 GHz and E = 2.14 GHz, for the longitudinal and axial parameters, respectively. These values are different from those proposed by [10] (D = − 8.63 GHz and E = 1.61 GHz) and by [5] (D = 11.99 GHz and E = 4.52 GHz). Conversely, the present results appear close to the set of parameters determined by [2], i.e. D = −10,812.0 (6) MHz, E = 1368.9 (4) MHz. The difference (within 31%) could be ascribed to the natural variability of the crystal-chemical settings in the natural amethyst crystals, tracing the specific physical and chemical conditions of crystal genesis and growth.

The experimental EchoEPR spectrum of the amethyst sample is shown in Fig. 1c. The most intense lines revealed by the cw spectrum are refocused after the chosen Hahn decay sequence. Due to the very fast relaxation times of high-spin Fe(III), normally it is impossible to use superhyperfine techniques like pulsed ENDOR or ESEEM to investigate such centres. Therefore, this is a very rare case, and, to the best of our knowledge, the only one in literature where ESEEM was recorded for a high-spin Fe(III) centre. We chose to carry out the time domain experiments on the line at 186.8 mT, which can allow us to focus on an EPR line arising from the Fe3+:H+ centre. Moreover, the signal-to-noise ratio is highly improved for this line.

4.2 ESEEM

The experimental time-domain spectra of the amethyst sample obtained after a two- and three-pulse sequence are shown in Fig. 2a, b, respectively. The spectrum of Fig. 2a exhibits a relatively fast decay, the initial intensity being reduced to less than one-tenth in about 800 ns. Superimposed to the decay, an intense and structured nuclear modulation is apparent. Multiple periods in the ESEEM can be envisaged. The spectrum in Fig. 2b, while marking a conceivably longer decay time, confirms the presence of a well-defined ESEEM, in which the occurrence of a single oscillation period ~ 100 ns is apparent.

Fig. 2
figure 2

2P (a) and 3P (b) time-domain spectra of the natural amethyst crystal, registered at 35 K and at the magnetic field value of 186.8 mT. The corresponding Fourier Transforms are illustrated in (c, d), respectively. The frequencies of the main FT peaks are indicated in the graphs

Full size image

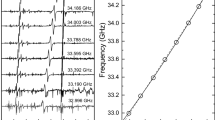
The Fourier Transforms of the 2P and 3P time-domain experiments (Fig. 2c, d, respectively) confirm the previous observations. In Fig. 2c four main peaks (at 4.16, 6.12, 10.25 and 16.38 MHz) can be highlighted, corresponding to two main frequencies and to their combinations (indicated in the Figure), whereas in Fig. 2d two peaks (at 6.12 and 10.28 MHz), corresponding to the main frequencies of Fig. 2c, are detected. Interestingly, the ratio between the amplitudes of the two peaks is largely favouring the second frequency.

4.3 Numerical Simulation of the ESEEM Patterns

Due to the fast decay of 2P ESEEM, when compared to the 3P one, and to the presence of only two main frequencies in the FT of the latter, the interpretation of the time domain experiments is better accomplished by a careful analysis of the FT of the 3P experiment, and using the 2P experiment as a useful a posteriori check. The analysis is grounded on a trial-and-error procedure involving the comparison of the FT features of the experimental ESEEM with the corresponding ones from a numerical simulation. The used computing code, ECHOGTH.FOR, provides the evaluation of the nuclear modulation patterns due to hyperfine (hf) isotropic and anisotropic interactions in the point-dipole approximation (in our case nuclear spin quantum number I = 1/2) following the Equations 46 and 48 in [12]. The program ECHOGTH.FOR is specifically designed to simulate a S = 1/2 system, so a question arises if our system, a S = 5/2, can be approximated to this. First of all, we set our field on the top of the line, at 186.8 mT. With our field perpendicular to the axis c of the crystal, theoretical calculations show that this line derives from the transition within the middle Kramer doublet of the S = 5/2 system (levels 3 and 4, Fig. 3).

Fig. 3
figure 3

Energy level diagram of the Kramer doublets for the Fe(III) site in amethyst in the experiment conditions: magnetic field perpendicular to the c crystal axis and D = − 10.1 GHz, E = 2.14 GHz. The double arrow indicates the transition originating the EPR line at 186.8 mT

Full size image

The two states corresponding to this Kramer doublet can be described as a mixing of the spin functions |ms > , with ms = − 5/2,…, + 5/2, and precisely:

$$|3\rangle = c_{{ - \frac{5}{2}}} | - 5/2\rangle + c_{{ - \frac{1}{2}}} | - 1/2\rangle + c_{{ + \frac{3}{2}}} | + 3/2\rangle$$
$$|4\rangle = c_{{ + \frac{5}{2}}} | + 5/2\rangle + c_{{ + \frac{1}{2}}} | + 1/2\rangle + c_{{ - \frac{3}{2}}} | - 3/2\rangle$$

where cms’s are 0.805, 0.638, − 0.192, − 0.402, − 0.561, − 0.656 for ms = − 5/2, − 3/2, − 1/2, ½, 3/2, 5/2, respectively.

Therefore, the + 1/2 and − 1/2 states contribute significantly to the levels 3 and 4 involved in the observed transition. As for the ESE, it derives from quantum coherences between the ms states. However, the coherences involving states with |mS|> 1/2 are relevant, in principle, but do decay fast due to their short relaxation times compared to the − 1/2, + 1/2 coherences [13]. Then, their contribution to the ESE is expected to be small. Since in the 3P experimental FT ESEEM just two frequencies are seen, it is sensible to assume that they come from the − 1/2, + 1/2 contributions, while the |ms|> 1/2 state coherences are likely completely relaxed on the timescale of our experiment. As a consequence, we expect ESE contributions from only − 1/2, + 1/2 coherences, resulting in ESE modulations at frequencies corresponding to an effective S = 1/2 spin system, and we are enabled to use ECHOGTH.FOR in our simulations.

In the simulation program, beside the parameters of the experimental setup, input parameters are required to determine the nuclear frequencies ωα and ωβ in the two manifolds of electron spin S = 1/2 (ge assumed isotropic), i.e. the distance r between the interacting spins, the angle θ of the r vector with the magnetic field B0 direction and the isotropic Fermi constant aiso. ESEEMs are calculated, by assuming axially symmetric dipolar interaction, at each θ ranging from 0° to 180° in steps of 5°; on the basis of literature data [2, 4, 5] aiso was allowed to range from 0.2 MHz (the minimum detectable) to 2.5 MHz with 0.1 MHz steps. For the distance, a limit value of 3.2 Å was chosen, on the basis of literature [1] and considering that, in contrast with the experiment, in the case of a single interacting proton at distances longer than 3.2 Å the modulation amplitude results very low. In the Fig. 4a the behaviour of the two nuclear frequencies as a function of the θ angle with aiso = 0.2 MHz at r = 2.7 Å and 3.0 Å is shown. Two similar features appear in both the trends: (a) the same frequency values occur in the points with θ = (90° + x) and θ = (90° − x), therefore only one region, either θ > 90° or θ < 90°, needs to be considered for a further analysis; (b) the crossing of the two frequencies at two θ values, 55° and 125°, even if the two trends do not overlap due to the different r. Note that one cannot a priori assign the proper labels ωα and ωβ to the FT experimental peaks; one can label the experimental frequencies as ωL (Low) and ωH (High). Indeed, the computation shows that the crossing between the two frequencies ωα and ωβ at the two θ values cited above alternates their role as ωH and ωL, and that this occurs at a frequency value which depends on the considered r value.

Fig. 4
figure 4

Diagram of the nuclear ωα and ωβ frequencies versus the angle θ of the r vector with the magnetic field B0 direction, calculated for two relevant r distance values, 2.7 and 3.0 Å, respectively (a); FT of the best fit simulated ESEEMs of the 2P (b) and 3P (c) experiments

Full size image

Taking into account these results and considering the experimental values of 3P FT 6.12 MHz and 10.28 MHz, we can limit the further analysis to the range 5° ≤ θ < 90°. Best-fit frequencies occur for r = 3.0 Å at θ = 75° (6.23 MHz and 10.22 MHz); for r = 2.7 Å the best frequencies occur at θ = 72° (6.3 MHz and 10.9 MHz). From the calculated FT the ratio RI = IL/IH of the amplitudes of the two peaks can be compared with the experimental value RI = 0.057. At r = 2.7, RI = 0.62; at r = 3.0, RI = 0.03. On these bases, the best-fit set of parameters appears r = 3.0 Å, θ = 75°.

To confirm this result, we compared the experimental 2P FT with the corresponding one computed with this set. The agreement is not satisfactory (Table 2). Since in the computation aiso = 0.2 MHz was assumed, we decided to increase this last parameter, but this gave worse results, both in the frequency values and in RI amplitude ratio, and the same occurred by changing the θ parameter by ± 5°.

Table 2 Comparison of experimental and simulated nuclear frequencies
Full size table

Accordingly, one must reconsider the value of the distance parameter. Indeed, in the 3P analysis r = 2.7 Å was abandoned due to its high RI value (0.45) when compared to the experimental one; however, the computation was done at constant aiso and θ. If we use r = 2.7 Å, a better agreement between the experimental and computed RI = 0.057 is reached using aiso = 2.0 MHz, and this generates main frequencies at 6.6 MHz and 10.3 MHz. This means that also θ has to be changed; the best agreement is obtained with θ = 80°, aiso = 2.5 MHz; the frequencies of the main and combination lines are: 4.17, 6.13, 10.28, 16.35, and RI = 0.059 (3P simulation) and RI = 1.0 (2P simulation). The best-fitted FT transforms are shown in Fig. 4b, c, whereas the list of the best-fit parameters shown in Table 3.

Table 3 Best fit parameters for the experimental ESEEM
Full size table

We checked also for the possibility of a negative aiso, maintaining the range 6.12–10.28 MHz for the two main frequencies. The effect on the values of the main frequencies due to the negative aiso with respect to the corresponding positive value is to decrease the ωL and to increase the ωH.

As a result, in the range of 70° < θ < 85°, negative aiso > − 0.2 MHz leads frequencies out of the established range both in the case of r = 2.7 Å and r = 3.0 Å. Using aiso = − 0.2 MHz, the best-fit frequencies 6.15 MHz and 10.31 MHz occur at θ = 74°, r = 3.0 Å; however, the ratio RI = 0.21 is considerably higher than the experimental value RI = 0.057 as well as higher than the best-fit RI = 0.059 calculated with positive aiso.

5 Conclusions

The best fit results of the simulation of the ESEEM spectra carried out on the natural amethyst sample allowed us to determine a distance between Fe(III) and the proton slightly larger than the one already reported in the literature: 2.7 vs 2.52 Å [1, 5] or 2.6 Å [4]. One has to keep in mind that differences in the values can arise from: slight differences in the experimental T values of measurements (although [4] suggest this phenomenon as negligible), different sensibilities of the techniques, intrinsic differences of the structural features of the defect centres in different natural crystals. The set of ZFS parameters refined in this study exhibits some similarity to that proposed by [9]. However, these authors attributed this centre to a proton bonded to the close oxygen to the Fe(III) centre. Conversely, concerning the S2(C) centre, [1] reported for this centre a Fe(III)-H+ distance of 1.94 Å, i.e. a distance fully unsuitable to explain the present results. Accordingly, we ruled out this attribution.

Moreover, the simulation provided two values for the angle between the segment linking Fe(III) and H+ and the direction of the magnetic field (in our experiment aligned along the y direction of the reference frame). These two values (80°, 100°) correspond to two equivalent structural solutions for the Fe(III):H+ centre.

A possible structural model of the defect centre can be thus proposed, taking into account some additional boundary conditions, all derived from the literature. First, the Fe(III) oxygen distance in the centre is 1.78 Å, as derived from XAS investigations [9]. Second, the oxygen-proton distance is 0.99 Å, as suggested by DFT calculations [9]. In Fig. 5a, a view of the Fe(III):H+ centre, corresponding to the solution for θ = 80°, is proposed. This model has been obtained by simultaneously fulfilling all the above-cited requirements. The tetrahedron is slightly distorted to account for a rhombic distortion, and this distortion is necessary to achieve the correct value for θ. The proton is accommodated in the channels parallel to the c-axis, that crosses the α-quartz structure (Fig. 5b). The occurrence of a non-negligible aiso value suggests that the orbital superposition between the paramagnetic centre and the proton is occurring, thus confirming the relative stability of this defect centre. The structural framework here discussed is in line with previous findings of the literature [4, 5], although the values of distances and angles are moderately different. A wide discussion about the similarity between the S2 and the [AlO4/H]0 centre in quartz is present in [4]. We suggest that the differences here discussed can be ascribed to the structural changes expected in tetrahedral having Al3+ or Fe3+ in their centres.

Fig. 5
figure 5

a Schematic model of the Fe(III):H+ centre. The magnetic field is aligned normal to ac plane, along the right direction. b Structural model of the α-quartz structure including the Fe(III):H+ centre. The magnetic field is aligned normal to ac plane, along the vertical direction

Full size image

In agreement with Cortezão et al. [9], only the occurrence of a high energetic event, such as a mechanical or radiative event, could provide the conditions to modify this centre. Finally, the authors want to emphasize how fundamental was the combination of paramagnetic techniques to ascertain the crystal-chemical nature of very diluted species in minerals, in a context where conventional methods (such as X-ray or neutron diffraction) are ineffective.