Hyperfine Interaction Promoted Intersystem Crossing

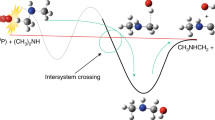
Abstract

The mechanism of the intersystem crossing (ISC) in planar aromatic hydrocarbons is revised by considering hyperfine interaction promoted singlet–triplet transitions. The density matrix of the spin system of the metastable triplet state is derived. Extra terms including the electron-nuclear ordering, the ordering between the magnetic nuclei of the molecule, and the coherence between the nuclear spin sublevels are shown to be developed during the ISC. Several peculiarities of the spin system are predicted. The results are compared with the properties generated by the optical nuclear polarization. The proposed mechanism is examined by a qualitative analysis of the available experimental data on photoexcited pentacene in p-terphenyl.

Appendix

1.1 Excited States

In general, ISC in photoexcited molecule is promoted by SOC, which mixes the excited singlet and triplet states and initiates the radiationless spin-forbidden transitions. The SOC in organic molecules can be evaluated in McClure’s central field approach [4] where all interactions of the one electron spin with the orbital moments of other electrons are neglected. It has been shown that the light-induced processes in aromatic hydrocarbons are adequately described in the one-electron approximation of the SOC within the four-electron model [27, 28]. This model includes the transitions of four electrons that are able to mix the close-lying ππ and πσ states. The influence of the rest of the electrons is ignored. This approach has been proven to be useful for the analysis of the radiative transitions in aromatic hydrocarbons [27, 28]. We are not interested in the origin of the mixing terms in SOC ISC transitions, so we restrict the description to a single electronic transition in which an electron moves from one π MO to another without the investigation of the possible intermediate steps involving the σ MOs. This situation occurs in photoexcited pentacene, where the metastable triplet state T₁ is believed to be populated via the transitions between the S₁ and energetically nearby T₃ states [29]. In this case, the properties of the states of interest are determined by the two unpaired electrons that occupy the Highest Occupied MO (HOMO) π and the Lowest Unoccupied MO (LUMO) π*. We label the HOMO as $\varphi_{a}$ and for simplicity, we assume that the excited electron changes its spin projection during the jump from the LUMO $\varphi_{b}$ to the MO $\varphi_{c}$.

The orbitals $\varphi_{a}$, $\varphi_{b}$ and $\varphi_{c}$ can be described in the approximation of a linear combination of the atomic orbitals (LCAO) as:

$$\varphi_{q = a,b,c} = \sum\limits_{n} {c_{q,n} p_{z,n} } .$$

(11)

Here $p_{z,n}$ is the out-of-plane 2p atomic orbital (AO) of the carbon atom in the position n, and c_q,n is its weighting coefficient.

The two-electron wavefunction of the first excited singlet state S₁ is defined as

$$\Psi_{\text{S}} = \left( {\left| {\varphi_{a} \alpha_{1} \varphi_{b} \beta_{2} } \right|-\left| {\varphi_{b} \beta_{1} \varphi_{a} \alpha_{2} } \right|} \right)/\sqrt 2 = \varphi_{\sigma } \sigma ,$$

(12)

where the indices 1 and 2 refer to unpaired electrons, and $\alpha$ and $\beta$ represent the spin states with the projections ± 1/2. The functions $\varphi_{\sigma }$ and σ describe the two-electron orbital and spin wavefunctions, respectively:

$$\begin{gathered} \varphi _{\sigma } = (\varphi _{{a_{1} }} \varphi _{{b_{2} }} + \varphi _{{b_{1} }} \varphi _{{a_{2} }} )/\sqrt 2 \hfill \\ \sigma = (\alpha _{1} \beta _{2} - \beta _{1} \alpha _{2} )/\sqrt 2 . \hfill \\ \end{gathered}$$

(13)

The excited triplet state participating in the ISC process is expressed as:

$$\Psi_{{{\text{T}},\eta = x,y,z}} = (\varphi_{a1} \varphi_{c2} - \varphi_{c1} \varphi_{a2} )\tau_{\eta } /\sqrt 2 = \varphi_{\tau } \tau_{\eta } ,$$

(14)

where the orbital and the spin wavefunctions are:

$$\begin{gathered} \varphi _{\tau } = (\varphi _{{a_{1} }} \varphi _{{c_{2} }} - \varphi _{{c_{1} }} \varphi _{{a_{2} }} )/\sqrt 2 \hfill \\ \tau _{x} = - (\alpha _{1} \alpha _{2} - \beta _{1} \beta _{2} )/\sqrt 2 \hfill \\ \tau _{y} = i(\alpha _{1} \alpha _{2} + \beta _{1} \beta _{2} )/\sqrt 2 \hfill \\ \tau _{y} = (\alpha _{1} \beta _{2} + \beta _{1} \alpha _{2} )/\sqrt 2 . \hfill \\ \end{gathered}$$

(15)

1.2 Spin–Orbit Coupling

The singlet and triplet states have different properties relative to the interexchange of the unpaired electrons. The singlet state is characterized by the antisymmetric spin part of the wavefunction and the symmetric orbital wavefunction (13), while the triplet (15) state has opposite symmetry relations. Typically, the spin subsystem is well isolated, and the ISC between the singlet and triplet states is limited by the rate of the processes mixing the spin states. Thus, the mixing of the singlet and triplet spin wavefunctions by SOC is the dominant ISC mechanism in diamagnetic complexes [1]. In McClure’s central field approach, the SOC Hamiltonian consists of only one-electron operators:

$$H_{\text{SOC}} = \sum\limits_{i} {\sum\limits_{\zeta = x,y,z} {\lambda_{i,\zeta } L_{i,\zeta } S_{i,\zeta } } } .$$

(16)

Here, the orbital angular momentum ${\mathbf{L}}_{i} = \sum {{\mathbf{l}}_{i,n} }$ of the electron i is a sum of the operators l_i,n. Each of these operators is defined with respect to the particular carbon nucleus n. The Hamiltonian (16) can be separated in two parts that are symmetric, $(\lambda_{1,\zeta } L_{1,\zeta } + \lambda_{2,\zeta } L_{2,\zeta } )(S_{1,\zeta } + S_{2,\zeta } )/2$, and anti-symmetric, $(\lambda_{1,\zeta } L_{1,\zeta } - \lambda_{2,\zeta } L_{2,\zeta } )(S_{1,\zeta } - S_{2,\zeta } )/2$, relative to interexchange of the unpaired electrons. Although both operators conserve the symmetry of the total wavefunction, they act differently on the spin and orbital parts. By the definition, the operator ${\mathbf{S}}_{1} + {\mathbf{S}}_{2}$ conserves the total spin multiplicity while the operator $\Delta {\mathbf{S}} = {\mathbf{S}}_{1} - {\mathbf{S}}_{2}$ mixes the singlet and triplet states:

$$\left\langle {\tau_{\zeta = x,y,z} } \right|{\mathbf{S}}_{1} + {\mathbf{S}}_{2} \left| \sigma \right\rangle = 0,\quad \left\langle {\tau_{\zeta = x,y,z} } \right|\Delta {\mathbf{S}}\left| \sigma \right\rangle = 1.$$

(17)

Thus the symmetric part of the SOC Hamiltonian (16) acts within the triplet manifold while the anti-symmetric part promotes ISC. The mixing matrix element $\left\langle {\varphi_{b} } \right|L_{i,\zeta = x,y,z} \left| {\varphi_{c} } \right\rangle$ can be expressed in the LCAO approach as a sum over the contributions from individual components $\left\langle {p_{z,k} } \right|l_{n,\zeta } \left| {p_{z,l} } \right\rangle$, where the indices n, k, and l run over the carbon atoms. By definition of the angular momentum, $\left. {l_{z,n} \left| {p_{z,k} } \right\rangle } \right|_{k = n} = 0$, and the components $l_{x,n}$ and $l_{y,n}$ rotate the AO wavefunctions from out-of-plane to in-plane AO and, therefore, they cannot mix the MOs (11) since they are all out-of-plane, i.e. $\left\langle {p_{z,k} } \right|l_{x,n} \left| {p_{z,l} } \right\rangle = \left\langle {p_{z,k} } \right|l_{y,n} \left| {p_{z,l} } \right\rangle = 0$. In addition, the angular momentum operator $l_{z,n}$ is not Hermitian and its value averaged over any real wavefunction is zero: $\left. {\left\langle {p_{z,k} } \right|l_{z,n} \left| {p_{z,l} } \right\rangle } \right|_{l = k} = 0$. Therefore, the singlet and triplet states can be mixed by only the relatively weak contributions with k ≠ n ≠ l [4]. Typically, the value ~ 0.1 cm⁻¹ is estimated for planar hydrocarbons [1, 5,6,7].

In general, the action of the SOC operator driving the singlet–triplet mixing can be expressed in the molecular frame as:

$$\begin{aligned} \left\langle {\Psi_{\text{S}} } \right|H_{\text{SOC}} \left| {\Psi_{T,\zeta = x,y,z} } \right\rangle & = \left\langle {\varphi_{\sigma } } \right|\lambda_{1,\zeta } L_{1,\zeta } - \lambda_{2,\zeta } L_{2,\zeta } \left| {\varphi_{\tau } } \right\rangle /2 = i\varLambda_{\zeta } \\ {\varvec{\Lambda}} & = \{ \lambda_{x} ,\lambda_{y} ,\lambda_{z} \} . \\ \end{aligned}$$

(18)

The vector Λ is chosen here to have real components and the imaginary unit reflects the purely imaginary nature of the orbital angular momentum operator acting on the pure real wavefunctions (13) and (15). Obviously, the approximations used here oversimplify the ISC and more complicated mechanisms, based on the SOC can be involved in this process [30, 31]. Nevertheless, no influence on the nuclear spin sublevels during the ISC is expected in absence of the HFI, and the total contribution of the SOC ISC can be described in terms of populations of the triplet sublevels determined by the vector Λ (18).

1.3 Hyperfine Interaction

The spin-Hamiltonian of the HFI can be written as:

$$H_{\text{HFI}} = \sum\limits_{i,n} {{\mathbf{S}}_{i} {\mathbf{A}}(\vec{r}_{in} ){\mathbf{I}}_{n} } ,$$

(19)

where A is a tensor of the HFI depending on the radius-vector r_in between the i-th electron and the nucleus (proton) in the position n, and I_n is the vector-operator of the nuclear spin. Based on the properties (17), it can be shown that the anti-symmetric part of the HFI mixes the singlet and triplet states:

$$\begin{aligned} \left\langle {\Psi_{\text{S}} } \right|H_{\text{HFI}} \left| {\Psi_{{{\text{T}},\zeta }} } \right\rangle & = \sum\nolimits_{n,\eta } {\text{A}_{n,\zeta \eta } I_{n,\eta } } ,\quad \zeta ,\eta = x,y,z \\ {\mathbf{A}}_{n} & = \left\langle {\varphi_{\sigma } } \right|{\mathbf{A}}(\vec{r}_{1n} ) - {\mathbf{A}}(\vec{r}_{2n} )\left| {\varphi_{\tau } } \right\rangle /2. \\ \end{aligned}$$

(20)

The most important difference between the Eqs. (18) and (20) is the presence of an additional operator I acting on the nuclear spin sublevels. The tensor A_n (20) can be expressed in LCAO approximation via the tensors ${\mathbf{A}}_{nk}$ describing the interaction between the nuclear spin in the position n and the electron spin localized in the k-th AO 2p_z (11):

$$\begin{aligned} {\mathbf{\rm A}}_{n} & = \sum\limits_{k} {\upsilon_{k} \left\langle {p_{z,k} } \right|{\mathbf{A}}_{nk} \left| {p_{z,k} } \right\rangle } \\ \upsilon_{k} & = c_{a,k}^{2} \delta_{b,c} - c_{b,k} c_{c,k} . \\ \end{aligned}$$

(21)

According to (21) the strength of the HFI depends on the positions of the carbon and hydrogen atoms and on the probabilities of finding the unpaired electrons in the corresponding 2p_z AO. Note, that for the sake of simplicity, we use the same indexes for the covalently bonded carbon and hydrogen atoms. The delta-function in expression (21) appears as a result of the orthonormality of the MOs (11): $\delta_{bc} = \left\langle {{\varphi_{b} }} \mathrel{\left | {\vphantom {{\varphi_{b} } {\varphi_{c} }}} \right. \kern-0pt} {{\varphi_{c} }} \right\rangle$. In the case in which the HFI mixes the lowest excited singlet and triplet states ($\varphi_{c} = \varphi_{b}$) the parameter $\upsilon_{k}$ determines the difference of the probabilities of finding the electrons of the orbitals $\varphi_{a}$ and $\varphi_{b}$ in the position k: $\upsilon_{k} = c_{a,k}^{2} - c_{b,k}^{2}$.

1.4 Intersystem Crossing

To describe the ISC, we begin by assuming that it occurs between the first excited singlet S₁ and the vibronically excited triplet state $T_{\text{v}}$ with the $\zeta$-th projection of the electron spin. In general, a molecule with n protons has $N = 2^{n}$ nuclear spin sublevels for each state of the electron spin. Thus, there are N eigenstates of the unperturbed singlet state spin-Hamiltonian, which have the form $\Psi_{{{\text{S}},i}} = \Psi_{\text{S}} \chi_{1} \ldots \chi_{n}$ with $i = 1, \ldots N$ where and the k-th nuclear spin is characterized by the wavefunction $\chi_{k}$. Similarly, there are N sublevels on the triplet state $T_{\text{v}}$, $\Psi_{\zeta ,i} = \Psi_{\zeta } \chi_{1} \ldots \chi_{n}$. Assuming that the first excited singlet state has no nuclear spin polarization, the non-normalized density matrix of the singlet S₁ at t = 0 equals:

$$\rho (0) = \sum\limits_{i = 1 \div N} {\left| {\Psi_{{{\text{S}},i}} } \right\rangle \left\langle {\Psi_{{{\text{S}},i}} } \right|} .$$

(22)

The antisymmetric parts of the Hamiltonians (16) and (19) mix this state with the triplet state $T_{\text{v}}$. The initial density matrix of the triplet state can be evaluated by non-stationary perturbation theory. The formal solution for the evolution of the singlet state in the linear approximation of the perturbation theory is [24]:

$$\begin{aligned} \left| {\Psi_{{{\text{S}},i}} (t)} \right\rangle & = \left| {\Psi_{{{\text{S}},i}} } \right\rangle + \sum\limits_{v,j} {g(\omega_{{{\text{v}},ij}} )\left( {H_{\text{SOC}} + H_{\text{HFI}} } \right)_{ij} \left| {\Psi_{{{\text{v}},j}} } \right\rangle } \\ g(\omega ) & = (1 - \exp ( + i\omega t))/\omega . \\ \end{aligned}$$

(23)

where $\hbar \omega_{{{\text{v}},ij}} = E(\Psi_{{{\text{S}},i}} ) - E(\Psi_{{{\text{v}},j}} )$ is the energy difference between the states of interest, which depend on the spin and orbital wavefunctions as well as on the vibronic modes of the initial and final states.

The operator $\left| {\Psi_{{{\text{S}},k}} (t)} \right\rangle \left\langle {\Psi_{{{\text{S}},k}} (t)} \right|$ determines the expectation value of finding the system in a particular state for the initial state determined by (23). Thus, the density matrix elements of the state T_v in the absence of the electronic relaxation to the metastable state T₁ are defined by the expression

$$\rho_{{{\text{v}},ij}} = F_{{{\text{v}},ij}} \sum\limits_{k} {\left\langle {\Psi_{{{\text{v}},i}} } \right|\left| {\Psi_{{{\text{S}},k}} (t)} \right\rangle \left\langle {\Psi_{{{\text{S}},k}} (t)} \right|\left| {\Psi_{{{\text{v}},j}} } \right\rangle } .$$

(24)

Here, the Frank–Condon factor F_v describes the overlap of the nuclear wavefunctions in the Born–Oppenheimer approximation. In the case of a high density of normal vibronic modes, the Frank–Condon factor is practically constant within the interval of variation of the energy splitting $E(\Psi_{{{\text{S}},k}} ) - E(\Psi_{{{\text{v}},i}} )$. Thus, the overlap of the nuclear wavefunctions in (24) can be approximated as being independent of the spin subsystem F_v,ij = F_v. However, it should depend on the electronic configuration of the intermediate triplet states that participate in the ISC. Indeed, several triplet states can be below the singlet state S₁ in aromatic hydrocarbons. In particular, three triplet states lie below S₁ in pentacene. Ab initio calculations have shown [32] that the state T₃ of pentacene is only about 10³ cm⁻¹ below the state S₁ while the lowest triplet T₁ state definitively lies more than 10⁴ cm⁻¹ below S₁. The overlap of the nuclear wavefunctions and the density of the vibronic modes strongly depend on the energy gap. Thus the Frank–Condon factor should depend on the state involved in the ISC and it can play an essential role in determining the relative contribution of the ISC channel.

The internal conversion from the state T_v to the lowest triplet state T₁ for large molecules like pentacene is expected to occur on a picosecond time scale. Thus, the spin state T₁ inherits the initial state of the spin subsystem T_v. Therefore, the density matrix of the metastable triplet state T₁ can be found by the integration of the expression (24) over the normal vibronic modes.

$$\tilde{\rho }_{\text{T}} = \sum\limits_{i,j} {\left| {\Psi_{{{\text{T}},i}} } \right\rangle \left\langle {\Psi_{{{\text{T}},j}} } \right|} \int\limits_{\text{v}} {{\text{d}}v\rho_{{{\text{v}},ij}} } .$$

(25)

The energy gap $\Delta_{ij} = E(\Psi_{{{\text{v}},i}} ) - E(\Psi_{{{\text{v}},j}} )$ does not depend on the vibronic mode and hence, $\Delta_{ij} = E(\Psi_{{{\text{T}},i}} ) - E(\Psi_{{{\text{T}},j}} )$. Expression (25) can be simplified assuming that the vibronically excited triplet states T_v near the S₁ state have a uniform distribution of vibronic modes. In this case, the zero point can be set at $\Delta /2 = \Delta_{ij} /2$ and the limits of integration can be set to plus and minus infinity. Under these conditions, the rate of the singlet–triplet transitions is proportional to the integral:

$$g_{2} (\Delta ) = \frac{1}{2\pi }\int_{ - \infty }^{\infty } {g^{*} (v - \Delta /2)g(v + \Delta /2){\text{d}}v} = ig(\Delta ).$$

(26)

Note, that the integral (26) is undetermined at $\Delta = 0$, however, its leading term can be derived as the limit $g_{2} (0) = \lim_{\Delta - > 0} g_{2} (\Delta ) = t$. This result is consistent with Fermi’s Golden rule, as expected for a first-order perturbation theory treatment [24]. In general, the mixing of the initial and final states depends on the mean lifetime τ of the excited singlet state and the coherence damping factor can be estimated as:

$$\begin{aligned} G(\Delta ) & = \bar{g}_{2} (\Delta )/\bar{g}_{2} (0) = 1/\sqrt {1 + (\Delta \tau )^{2} } \\ \bar{g}_{2} (\Delta ) & = \int_{0}^{\infty } {g_{2} (\Delta )\exp ( - t/\tau ){\text{d}}t/\tau } . \\ \end{aligned}$$

(27)

From (27) it is clear, that the transitions between two states become inefficient when the lifetime of the excited singlet state τ exceeds the inverse of the energy gap Δ between these states. The lifetime of the singlet state in hydrocarbons is well examined by the transient fluorescence spectroscopy. In particular, the fluorescence lifetimes 5–20 ns are found for anthracene, tetracene and pentacene in p-terphenyl [33]. The typical values of the HFI in aromatic hydrocarbons are in the range 10–20 MHz. Thus, the inverse of the HFI frequency is comparable with the lifetime of the singlet state and the coherence of the nuclear sublevels should not average during the ISC.