1 Introduction

Going to high and ultrahigh static magnetic fields and corresponding higher resonance frequencies was proved to open a broad range of new fascinating applications in magnetic resonance imaging [1, 2]. However, the construction of high-field magnetic resonance imaging (MRI) instrumentation poses severe technical challenges. One of the fundamental problems arises from the shortening of the electromagnetic wavelength in high-permittivity biological tissues, leading to a wavelength of about 27 cm for the proton resonance frequency of 125 MHz at 3 T and to 12 cm for 297 MHz at 7 T [3]. Therefore, in high-field MRI the generation of homogeneous B 1 fields within the human torso at 3 T and even in human head at 7 T is no longer feasible with a single radio-frequency (RF) transmit coil which makes the application of multi-element RF coil arrays a necessity [4]. By combining spatially varying B 1 profiles of single elements arranged around the imaged object in a phased array it is possible to mitigate B 1 inhomogeneity during RF excitation as well as to improve homogeneity of sensitivity profiles during signal reception [5].

Once introduced for B 1 homogenization coil arrays opened fascinating possibilities for parallel acquisition [6, 7] and parallel excitation techniques [8–10]. In parallel acquisition, the variation of sensitivity profiles of multiple receive coil elements across the imaged object is used to partially substitute gradient encoding, thereby reducing imaging time or increasing image resolution. In parallel excitation techniques, the excitation across multiple coil elements with different excitation field profiles made spatially selective pulses applicable [11]. Together with the travelling wave approach [12] parallel excitation is the most promising way to improve B 1 homogeneity in ultra high-field MRI [13]. In addition, parallel excitation opens the door for novel applications in the areas of volume selective excitation for MRI spectroscopy, reduction of the field of view, perfusion imaging [11] and mitigating susceptibility dephasing in functional MRI (fMRI) [14, 15].

Parallel MR techniques impose new requirements on RF coils and request the development of a new generation of multi-element RF arrays [16]. In parallel acquisition, the coil geometry determines the signal-to-noise ratio and maximum imaging reduction factor [17]. In parallel excitation technology, the specific absorption rate (SAR) of the spatially selective excitation pulse can be strongly reduced via optimization of coil array geometry [13]. One potential strategy to optimize spin excitation and signal reception is to design a coil array that allows for the adjustment of the coil geometry to the individual subject or other application needs. In this way, the geometry factor would be optimized and the higher B 1 field close to the coil conductor could be better utilized leading to a higher ratio of unloaded to loaded Q-factor for each coil element.

Parallel acquisition already led to a multitude of applications in clinical scanners where receive-only coil arrays are routinely applied for signal detection, while excitation is performed with a single-channel body coil. To achieve the same state of application for parallel excitation techniques the development of multi-element local transmit and receive coils is mandatory, allowing an optimized implementation of parallel acquisition and parallel excitation in the same coil setup.

The major challenge while designing and constructing transmit and receive coil arrays is to control the mutual electromagnetic coupling between the array elements. Coupling may lead to constructive and destructive interferences of the transmitted RF fields within a typical volume of excitation. Furthermore, RF power is lost due to parasitic currents induced in the coils coupled to the excited coil element. This fact poses severe restrictions to peak power demanding MR applications as, e.g., MR spectroscopy. Since coupling between the elements strongly depends on the coil load, adaptation of the coil array to different patients requires tedious iterative tuning and matching steps. These problems are aggravated when going to higher fields and higher RF frequencies and may be avoided only by the design of alternative RF coil schemes.

For receive-only coils, coupling is usually reduced by the use of preamplifiers with high input impedance, suppressing currents induced by the neighboring elements [4]. It is not possible to apply the direct analog of this preamplifier decoupling to transmit arrays due to the impedance match required for maximum power deposition efficiency.

Reactive coupling within an array coil can be compensated either inductively by properly chosen mutual arrangement of the individual elements [13] or by placing suitable capacitors between neighboring elements. This solution works well for a rigid arrangement of coil elements but it is only seldom applicable if geometrically flexible arrays are desired [18]. To compensate reactive coupling in an n-element array externally, a n × n decoupling network matrix is needed [19]. Tedious iterative readjustment of all its elements is necessary to adopt such a network to changes in geometry or load, which strongly limits the applicability of this approach.

Alternatively, the Cartesian feedback approach introduced by Hoult [20] for decoupling of transmit–receive elements could be used. Here, a high level of decoupling is achieved by feedback via pick-up coils. The major limitation of this solution is a narrow decoupling frequency band, a severe constraint for parallel excitation techniques, where broad-band pulses are needed for selective excitation [21].

A promising approach to actively decouple the array elements during transmission was proposed by Kurpad et al. [22, 23]. Using voltage-controlled metal–oxide–semiconductor field-effect transistors (MOSFETs) as current sources they managed to gain independent control of the currents in a multi-coil array. An additional benefit of the active decoupling is the reduced influence of sample loading on the resonance frequency, thus eliminating the need for iterative tuning and matching procedures for each subject.

Implementation of these current elements solved the problem of decoupling during transmission, however, the coil elements presented in Refs. [22, 23] are not designed for signal reception.

In this article we present a novel Current CONtrolled Transmit And Receive coil element (C2ONTAR-coil) for parallel transmit and receive applications. Improved decoupling in both modes was achieved by combining a current source as introduced by Kurpad et al. [22, 23] for transmission with a specially designed transmit–receive switch that allows for preamplifier decoupling for reception. The intrinsically decoupled elements were combined in arrays of flexible geometry. To evaluate the performance of the presented design in comparison with conventional transmit–receive elements, the results of the first proof of principle comparative study implementing parallel acquisition and parallel excitation experiments are presented.

2 Methods

2.1 C2ONTAR Elements

The electric scheme of the C2ONTAR element is shown in Fig. 1a. Figure 1b shows the RF-scheme of the C2ONTAR element without preamplifier and current sheet antenna (CSA) element. All used components are specified in Table 1.

Fig. 1
figure 1

Electrical scheme (a) and photograph (b) of the C2ONTAR element. The scheme is intersected in four blocks: (i) transmission block; (ii) resonant MR coil element and resonant transmission line; (iii) MR signal reception block; and (iv) transmit–receive switch. All used components are specified in Table 1

Full size image
Table 1 Specifications of RF-components used for construction of C2ONTAR elements
Full size table

For clarity Fig. 1a is divided into four blocks: (i) transmission block including RF current source and matching input network; (ii) coil block with the resonant MR coil element and resonant transmission line; (iii) MR signal reception block consisting of a low-input impedance preamplifier and the resonant transmission line, and (iv) the transmit–receive switch. The construction and working principles are described in the following.

2.1.1 Block (i)

The core unit of the transmit RF current source consists of a power MOSFET (BLF245, Philips Semiconductors), which is, due to its nickel content, slightly magnetic. The transistor’s operating point is controlled by two direct-current (DC) voltages, V D (drain voltage) and V G (gate voltage), to achieve a current source-like behavior and A-class operation mode. During transmission V D is switched on by the transmit–receive switch and V G = 3 V is overlaid by the input RF signal fed in via an input matching network. The output RF current of the MOSFET is controlled by the input RF signal and V G only, thereby suppressing parasitic currents induced by mutual electromagnetic coupling between neighboring array elements. In this way, effective decoupling of the individual coil elements in the array is achieved by controlling the coil’s currents during transmission. It is worthwhile noting here that, that the amplitude of the output current of the C2ONTAR element is restricted by the MOSFET’s half value of the maximum drain current (here 6 A). In practical applications the RF-current amplitude has to be further reduced to stay within the linear regime of the MOSFET.

2.1.2 Block (ii)

The RF coil element consists of a series LC resonant circuit which is tuned to the proton resonance frequency, in our case to 125.3 MHz. Impedance of the resonant circuit is determined by the resistive impedance of the coil load R l when tuned to the resonance frequency. The MR coil is connected to the circuitry by a 76-cm long RG58 cable, which constitutes a resonant λ/2 transmission line. Thereby, the slightly magnetic RF elements and static magnetic fields generated by DC currents of the current source are more remote from the imaged object to avoid B 0-field inhomogeneities degrading the image quality [23]. Due to the resonant properties of the transmission line the low-input impedance of the series resonant circuit is translated to the output of the current source and allows direct current control in the resonant element.

2.1.3 Block (iii)

To form a high-impedance preamplifier in the reception mode, a low-input impedance preamplifier is connected to the MR coil via the λ/4 transmission line and a series resonant circuit. The input impedance of the used GaAsFET preamplifier (Advanced Receiver Research, Burlington, CT, USA) was 10 Ω. The resonant line transforms the low-input impedance of the preamplifier into the high-input impedance according to [24]:

$$ Z = \frac{{Z_{\text{line}}^{2} }}{{Z_{\text{in}} }} = \frac{{(50\,\Upomega )^{2} }}{10\,\Upomega } = 250\,\Upomega. $$
(1)

High load impedance during reception limits the current in the RF coil, thus reducing inductive coupling between adjacent elements. In this way preamplifier decoupling during signal reception is achieved. Here we have to note that for the amplifier type used in this work, high impedance at the input can compromise a noise figure and thus reduce the signal-to-noise ratio. The reception efficiency can be further improved using a lower impedance preamplifier.

2.1.4 Block (iv)

Switching between transmission and reception is realized in the following way. During transmission the drain DC voltage V D = 24 V of the power MOSFET is switched on by an external trigger pulse (TTL-inp). The drain voltage adjusts the power MOSFET to its working point, and the drain current opens the PIN diodes D 1 and D 2 (MA4P4006F, M/A-COM). Opening of diode D 2 grounds the input of the preamplifier via the small impedance of the capacitance C 2 + C 3. In this way the receive block is isolated during transmission of high-frequency signals. Shutdown of diode D 1 during reception isolates the input of the signal preamplifier from the noise of the power MOSFET.

The theoretical limit of the decoupling achievable with a MOSFET-based current source is determined by the MOSFET’s parasitic output capacitance C p [22]. As was shown by Kurpad et al. [22, 23], decoupling is determined by the relation:

$$ K = - 20\log_{10} \frac{{R_{1} }}{{\sqrt {(\omega C_{p} )^{ - 2} + R_{1}^{2} } }}. $$
(2)

With C p of 75 pF and coil load resistance R l of 2 Ω, we expect an additional decoupling of 18.6 dB at 125.3 MHz for the MOSFETs used in this work.

2.2 Four-Element Head Array

We constructed two geometrically identical four-element CSA arrays [25] for human head imaging at 3 T, to evaluate the performance of the C2ONTAR elements in state-of-the-art imaging techniques and to compare them with conventional power source-driven elements. Parallel acquisition and parallel excitation experiments were performed with both setups and used for comparison. The first array consists of four C2ONTAR–CSA elements, while the elements of the second array were matched to a 50-Ω input impedance and driven by conventional power sources. Schematic views of C2ONTAR and power source-driven CSAs together with their electrical schemes are given in Fig. 2a and b, respectively.

Fig. 2
figure 2

Top Schematic views of C2ONTAR–CSA (a) and power source-driven CSAs (b). Bottom Electrical schematics of C2ONTAR–CSA (a) and power source-driven CSAs (b)

Full size image

In both cases the inductive loop of the CSA is formed by four plates of copper-clad base material with the size of 30 mm × 80 mm × 160 mm. The thickness of the copper layer (9 μm) was chosen to minimize eddy currents induced in the CSA by switching gradients during the MRI experiment.

The C2ONTAR–CSA element has three 5-mm gaps on the upper plate of the resonant circuit (see Fig. 2a). Distributed fixed and tuneable capacitors were placed into both outer gaps, providing adjustable capacity in a range from 19.5 to 28.5 pF. The element represents a series resonant circuit at 125.3 MHz. The third gap is used to connect the output of the resonance transmission line RF-in. Tuning of the resonant element to the proton resonance frequency of ω = 2π·(125.319 MHz) was achieved by adjusting the tuning capacitor to C t = 1/(ω 2 L), where L is the inductance of the element. We would like to stress here that, unlike conventional coils, for C2ONTAR elements the optimal value for the tuning capacitor does not depend on the element load R l.

For the power source-driven CSA shown in Fig. 2b, the upper part of the sheet was intersected by a 5-mm gap in which a variable capacitor C t was placed for tuning. The element represents a resonant circuit. It was inductively coupled to the 50-Ω transmission line by an inductive coupling loop inside of the rectangular block. Critical matching to the impedance of the transmission line was realized with the help of the tuning capacitor C t and matching capacitor C m. First, by changing C t, the real part of the input impedance of the port AB was adjusted to 50-Ω [24]

$$ \text{Re} (Z_{\text {AB}} ) = \frac{{\omega^{2} L_{\text {m}}^{2} R_{\text {l}} }}{{R_{\text {l}}^{2} + \left( {\omega L - \frac{1}{{\omega C_{\text {t}} }}} \right)^{2} }} = Z_{0} = :50\,\Upomega, $$
(3)

where L m is the mutual inductance of the coupling loop and resonance circuit. As the second step, the imaginary part of the impedance of port AB, Im(Z AB), was compensated by adjusting the trimmer capacitance C m

$$ \text{Im} (Z_{\text {AB}} ) = \omega L_{\text {m}} - \frac{{Z_{0} }}{{R_{\text {l}} }}\left( {\omega L - \frac{1}{{\omega C_{\text {t}} }}} \right) = :\frac{1}{{\omega C_{\text {m}} }}. $$
(4)

It becomes apparent from Eqs. (3) and (4) that the values of the tuning and matching capacitors have to be changed depending of the load R l. This implies a readjustment of the power source-driven CSA for every experiment or subject. For an electromagnetically coupled multi-element coil array, R l also depends on the tuning of the neighboring coils. This fact makes the application of the aforementioned iterative tuning and matching procedure mandatory to adjust the element to the resonance frequency and to avoid power reflection, which constitutes a major drawback of a conventionally driven coil array.

Four elements of each kind were combined to the head array shown in Fig. 3, each with its long axis parallel to the magnetic field direction.

Fig. 3
figure 3

Four-element C2ONTAR–CSA array with a head-sized cylinder gel phantom

Full size image

All phantom experiments were performed with a head-sized cylindrical agarose gel phantom (inner diameter (i.d.), 19 cm; length, 19 cm) as described in Ref. [25]. The electrical properties and relaxation times of the phantom gel were roughly that of brain tissue (ε = 76, σ = 0.33 S m−1).

2.3 Finite-difference time-domain (FDTD) Simulations

We performed electromagnetic field simulations for all considered coil configurations to understand the influence of RF driving conditions on measured B 1 field distributions: (1) a single CSA, (2) the four-element CSA array, (3) a single C2ONTAR–CSA element, and (4) the four-element C2ONTAR–CSA array. To this end numerical simulations were performed using the XFDTD 6.4 software (REMCOM, State College, PA, USA). The models were implemented on a 2-mm grid consisting of 200 × 200 × 200 cells together with seven perfectly matched layers to achieve free space behavior. The CSAs and C2ONTAR–CSAs were assumed to consist of planar sheets of perfectly conducting material. All capacitors were simulated by dielectric bars filling the 5-mm gaps on the upper plate of the resonant element. The dielectric constant of the bars was adjusted to tune the coil elements to 125 MHz. The load was modelled as a homogenous cylinder (D = L = 200 mm) with εr = 76 and σ = 0.33 S m−1, omitting the small influence of the Perspex walls (εr ≈ 2) on the dielectric properties of the phantom. The distance from the surface of the load to the bottom face of each element was set to 20 mm in general. For the single C2ONTAR–CSA simulation additional runs were performed for distances varying from 6 to 30 mm. RF excitation of the coil elements was accomplished either by driving a C2ONTAR–CSA directly by a current source or using a coupling loop inside the CSAs (Fig. 2b). In the later case lumped element complex valued resistors at the feeding points were iteratively adjusted to achieve the matching condition, i.e., zero reflection at all feeding ports (power matched mode of operation).

2.4 Bench Experiments

In the first step, the conventionally power source-driven CSA array was compared to the C2ONTAR–CSA array of identical geometry in bench experiments. The linearity of RF-voltage to current conversion was measured in a pick-up coil experiment.

The coupling of the CSA elements in transmit and receive mode was directly determined via the measurement of the two-port S parameters. To measure the coupling between two C2ONTAR–CSA elements we used the procedure described in Ref. [20]. Broadband pick-up loops were placed in fixed positions inside of the C2ONTAR–CSA elements. Voltages induced in the pick-up coils during the transition of each RF-element were measured by an oscilloscope. Since voltages induced in the pick-up coils are proportional to the currents of RF elements, they were used to estimate the decoupling matrix of the C2ONTAR–CSA array.

2.5 B 1 Measurements

The excitation profile of RF elements during transmission and sensitivity profiles during reception were determined by the circularly polarized components B +1 and B −1 of the B 1 field, respectively [26]. Relative B −1 maps of each element were obtained by dividing the images obtained with single element by the sum-of-square image of all elements [11]. In this way only relative B −1 maps can be measured. In addition, we measured the absolute values of B +1 by means of a preparation pulse method [25]. The fast gradient echo images of an axial slice in a cylinder phantom were acquired after an inversion pulse of varying power. By fitting the dependence of the signal intensity onto the amplitude of the inversion pulse, local B +1 values for each power level were determined.

2.6 Parallel Acquisition

Performances of C2ONTAR–CSA array in parallel acquisition were evaluated by performing in vivo sensitivity encoding (SENSE) experiments on a human subject.

These experiments were performed in compliance with the institutional guidelines for those studies. We applied a two-dimensional (2-D) fast low-angle shot (FLASH) (T E/T R = 11.2 ms/100 ms) sequence with a resolution of 256 × 256 and a field of view of 256 mm × 256 mm. The ‘worst case’ local SAR for the FLASH sequence applied and the cylindrical C2ONTAR–CSA array was estimated to be 0.5 W kg−1 which is well below the limit of 20 W kg−1 [25, 27]. The thickness of an axial slice was 10 mm. Based on sensitivity maps and noise correlation matrices measured prior to the experiments, the g-factor was calculated by applying the relation [6]

$$ g(r) = \sqrt {\left[ {{\mathbf{S}}^{H} {\varvec{\Uppsi}}^{ - 1} {\mathbf{S}}} \right]_{r,r'}^{ - 1} ({\mathbf{S}}^{H} {\varvec{\Uppsi}}^{ - 1} {\mathbf{S}})_{r,r'} }, $$
(5)

where S is the coil sensitivity matrix, Ψ is the noise correlation matrix, r′ is the coordinate of all aliased points.

2.7 Parallel Excitation

C2ONTAR–CSA array performance in parallel excitation was evaluated by an extension of the transmit SENSE method introduced by Katscher et al. [8].

In our experiments we used a 16-turn spiral excitation k-space trajectory during excitation with a slew rate of 91.1 Tm−1 s−1. After selective excitation, the 3-D fast-gradient echo images (T E/T R = 7 ms/100 ms) were acquired to sample the spatially selective excitation patterns. The size of the target pattern was 32 × 32 voxels with a field of excitation of 256 mm × 256 mm, N t = 16 × 64/R, where R is the reduction factor. Experiments with a reduction factor of 2, 3.2 and 4 were performed. The lengths of the excitation pulses were 6.36, 3.98, and 3.178 ms, respectively.

3 Results

3.1 FDTD Simulation

The inductance L of the resonant CSA element (see Fig. 2) was calculated from the imaginary part of the impedance on the input port obtained from FDTD simulation of the CSA element with capacitors removed. Thus, the value of capacitance C t can be estimated from the resonance condition (C t = 1/(ω 2 L)) to be 25 pF, which is in a good agreement with the value of tuneable capacitors of the C2ONTAR element.

The imaginary part of the impedance obtained from the simulations was not dependent on the load, decreasing only 0.5% with the change of the distance to the phantom from 30 to 6 mm. The real part of the impedance representing the induced coil losses critically depends on the distance to the phantom. It changes by 320% from 0.15 Ω at 30 mm to 0.47 Ω at 6 mm as results from the FDTD simulations.

For the C2ONTAR CSA element driven by 1 A amplitude of RF current and the distance between the phantom and RF current of 20 mm, the total power absorbed in the phantom was calculated to be 0.1091 W.

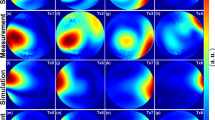
When comparing the simulated B 1 distributions for a single C2ONTAR–CSA element with the B 1 distributions for the same element within the four-channel C2ONTAR–CSA array, as expected, no significant differences can be observed. Hence, only field distributions for the latter case are displayed in Fig. 4.

Fig. 4
figure 4

Simulated and experimentally measured absolute B 1 + and relative B 1 − field magnitude maps in an axial slice of a head-sized cylinder phantom: a B 1 maps of a single power-matched CSA element arranged at the position corresponding to element 1 in Fig. 3; b B 1 maps of a single element of the four-element CSA array (Fig. 3) with power-matched elements; c B 1 maps of a single element of the comparable four-element C2ONTAR–CSA array. The absolute B 1 + maps of current-controlled elements are normalized to the amplitude of the RF current of 1 A on the input port of the element. The B 1 + maps of the power source-driven elements correspond to the absorbed power of P = 0.1091 W

Full size image

3.2 Bench Experiments

The relation of loaded to unloaded Q was estimated to be 2.5 for a single conventional CSA element.

The coupling matrices of the four-element array of power source-driven CSA and C2ONTAR–CSA were measured to be:

$$ {\mathbf{K}}_{CSA} = - \left[ {\begin{array}{*{20}c} 0 & {10} & {15} & {11} \\ {12} & 0 & {11} & {15} \\ {15} & {11} & 0 & {10} \\ {12} & {16} & {11} & 0 \\ \end{array} } \right]{\text{dB}};\;{\mathbf{K}}_{\text{CONTAR}}^{Tr} = - \left[ {\begin{array}{*{20}c} 0 & {24.5} & {30} & {25} \\ {25.5} & 0 & {25} & {32} \\ {30} & {25} & 0 & {26} \\ {25} & {32} & {25} & 0 \\ \end{array} } \right]{\text{dB}};{\mathbf{K}}_{\text{CONTAR}}^{Rs} = - \left[ {\begin{array}{*{20}c} 0 & {25} & {34} & {25} \\ {26} & 0 & {26.5} & {34} \\ {30} & {25} & 0 & {25} \\ {25} & {34} & {26} & 0 \\ \end{array} } \right]{\text{dB}}; $$

where K CSA is the coupling matrix of the power source-driven CSA array, \( {\mathbf{K}}_{\text{CONTAR}}^{Tr} \) and \( {\mathbf{K}}_{\text {CONTAR}}^{Rs} \) are the coupling matrices of the C2ONTAR–CSA array during transmission and reception, respectively. The coupling values are given in dB and the numeration of elements is shown in Fig. 3.

Due to the symmetry of the coil array, the matrix K has two independent values corresponding to coupling to the nearest neighbor and to the opposite element. The coupling matrices for transmission and reception are equivalent for the power source-driven CSA since the 50-Ω input impedance of the transmitter is equal to the input impedance of the receiver. The matrices depict couplings of the four C2ONTAR matrix elements in transmission (\( {\mathbf{K}}_{\text{CONTAR}}^{Tr} \)) and reception (\( {\mathbf{K}}_{\text {CONTAR}}^{Rs} \)) modes. It becomes apparent that in comparison to the power source-driven CSA array the C2ONTAR elements show in average additional decoupling of 14 dB in transmission and 15 dB in reception, in reasonable agreement with our estimation (Eq. (2)).

3.3 B 1 Sensitivity Maps

Color-coded maps of single-element B +1 and B −1 magnitudes obtained from the FDTD simulations and experimentally measured for a central axial slice of the head-sized cylinder phantom are shown in Fig. 4. Figure 4 shows maps for a single uncoupled CSA element (row a), for the single element of four CSA element array of Fig. 3 (row b) and for the single element of four C2ONTAR element array (row c). The results of the FDTD simulation are given in the first column, the experimentally measured absolute B +1 maps in the second column, the experimentally obtained relative B −1 maps in the third column of Fig. 4.

The simulated and experimentally measured B +1 maps of current-controlled elements (Fig. 4b, c) are normalized to the RF current amplitude of 1 A on the input port of the element. According to the FDTD simulation of single current-controlled element this current amplitude corresponds to the absorbed power of P = 0.1091 W. Therefore, simulated and experimentally measured B +1 maps for power source-driven elements are normalized to the absorbed power of P = 0.1091 W, to allow a quantitative comparison with current-controlled elements. Since only relative B −1 maps were measured, they are presented in arbitrary units.

Figure 4a shows simulated and experimental B +1 and B −1 maps of a single power source-driven CSA. The position of the single CSA element corresponds to the position of element 1 in Fig. 3. The B 1 amplitude decreases with increasing distance from the element. Influenced by RF eddy currents in the lossy phantom material, B +1 and B −1 profiles are asymmetrical and not identical to each other. In accordance to the reciprocity theorem, B +1 and B −1 can be transformed into each another by inverting the direction of the B 0 field [25]. Good agreement was obtained between simulation and experimentally measured B +1 maps.

Figure 4b shows the simulated and experimental B +1 and B −1 maps of the four-element power source-driven CSA array, when only element #1 was used for transmission. The B +,−1 maps for the other elements may be derived by 90°, 180° and 270° rotations around B 0, respectively. Due to electromagnetic coupling between the elements the B +1 and B −1 maps of the power source-driven CSA in the array differ strongly from those obtained with the isolated CSA element (Fig. 4a). This difference may be rationalized by the fact that while CSA #1 is transmitting, secondary currents are induced in CSA #2, #3 and #4 resulting in additional B 1 fields. Destructive interference of B 1 fields from different elements then leads to zero B +,−1 amplitude in several areas—so-called transmission and reception holes.

Figure 4c shows the analog results for the C2ONTAR–CSA array. These B +1 and B −1 maps differ drastically from those of the power-driven CSA array in Fig. 4b; they rather resemble the field maps of the single uncoupled CSA element, which clearly indicates the diminished coupling between the elements during transmission and reception.

The absolute B +1 field amplitude in the center of the cylinder phantom, generated by all four C2ONTAR–CSAs driven in the circular polarized (CP) mode with the maximum obtainable RF current of 3 A, was measured to be 2 μT. This value is in reasonable agreement with the simulation result of 3 μT for the same mode of operation, taking into account RF losses of the used components.

3.4 Parallel Reception

Figure 5 shows parallel acquisition results obtained with the four-element C2ONTAR–CSA array. In the top line SENSE-FLASH images of the human head are depicted, recorded with acceleration factors of two, three and four. The bottom line depicts g-factor maps for these reduction factors. The array shows good image quality and reasonable g-factor values as long as the reduction factor is less than the number of elements, which is a fundamental limitation for parallel acquisition [16]. This experiment demonstrates the feasibility of the parallel acquisition with inherently decoupled C2ONTAR element arrays.

Fig. 5
figure 5

Parallel imaging with the four-element C2ONTAR–CSA array (analog to Fig. 3) in vivo. Top, from left to the right: SENSE images recorded with the undersampling factor of 2, 3.2 and 4. Bottom corresponding g-factor maps

Full size image

3.5 Parallel Excitation

Figure 6 shows on the very left the target pattern for a parallel excitation experiment with the C2ONTAR array. The next images are excitation profiles of a spatially selective pulse with that target pattern and field of view reductions of 2, 3.2, and 4 (from left to right), corresponding to a gradient spiral trajectory during the pulse with 16, 10, and 8 turns, respectively. The excitation profile of the pulse with a 16-turn spiral shows a very good spatial selection; with a reduction factor of 4, the image quality is clearly affected by folding artefacts on the periphery. In analogy to parallel acquisition this result is in correspondence with the fundamental limitation of parallel excitation, where in both cases the maximum reduction factor is equal to the number of array elements.

Fig. 6
figure 6

Selective excitation in transmit SENSE experiment with the four-element C2ONTAR–CSA array (comparable to Fig. 3) in an axial slice of the cylinder gel phantom. From left to the right: target pattern, selective excitation with 16, 10 and 8 turns spiral gradient trajectory

Full size image

4 Discussion and Conclusion

We have presented a current-controlled transmit and receive MR coil array, employing a novel RF circuit, which allows to solve the problem of inherently coupled coil elements without complicated feedback circuits [28]. By spatial separation of the current source and coil element using an appropriate RF transmission line, the coil current can be controlled without distortions of the B 0 magnetic field homogeneity, which is a major concern in parallel excitation experiments as well as in echo planar imaging.

Since the presented implementation of C2ONTAR is a proof of the principle only, we will discuss only a few limitation of the concept. One technical limitation of C2ONTAR elements is the fact that the RF current in a single element is limited to half the maximum drain current of the power MOSFET. For our particular transistor type, this limit was 3 A resulting in a maximum achievable B +1 field amplitude of 2 μT in the center of the head-sized phantom. A possible way to increase this maximum B +1 amplitude would be the use of push–pull current sources [23, 29] together with high DC voltages. The preferred alternative, however, to partly overcome this limitation is to increase the number of C2ONTAR elements in the coil array. In this way, the maximum B 1, which is the superposition of B 1 fields of many elements, can be increased by keeping the maximum RF current in each element the same. Due to their intrinsic properties C2ONTAR elements are particularly suitable for this multi-element array applications, since no manual coil decoupling is needed. Thus, the major challenge in the construction of multi-coil transmit–receive arrays is solved this way. Additional amplification of the RF input signal in the C2ONTAR element makes them suitable to be used in low-cost transmit channels based on digital RF pulse generators [30], thus completely avoiding the need of expensive RF-power amplifiers.

In general, decoupling of RF array elements is not a necessary condition for performing parallel excitation or parallel acquisition. The performance of an array in parallel acquisition and parallel excitation is solely determined by the array geometry and the properties of the imaged object, and cannot be changed by element decoupling [31]. However, internal decoupling opens the opportunity to combine C2ONTAR elements in flexible adjustable arrays avoiding time-consuming iterative tuning, matching and decoupling procedures. This allows increased sensitivity and improved performance of the parallel acquisition and parallel excitation methods by directly optimizing the array to the size and shape of every subject, every imaged region or even to particular excitation target patterns.

One useful characteristic property of the C2ONTAR elements in comparison with power source-driven elements is the weak dependence of the B 1 amplitude on coil loading. For the conventional power source-driven element in the case of perfect matching, all incoming RF power is absorbed by the load. This means that for a higher loading factor, lower B 1 amplitudes are achieved at the same input power. In contrast to conventional coil arrays, the RF current for C2ONTAR elements is directly controlled by the input signals. Consequently, the B 1 fields are hardly affected by the loading factor. The remaining influence of the load’s dielectric losses on the B 1 field due to RF eddy currents is significantly weaker than for power source-driven RF elements. Due to this fact the B 1 fields and consequently RF pulse flip angles generated in C2ONTAR elements are robust against movements or changes in the imaged object’s size or conductivity. This valuable property may lead to improved image quality in applications like cardiac imaging where the B 1 profiles have to be stable against respiratory or cardiac motion. In addition, for a given distribution of ε and σ the SAR for C2ONTAR is determined by the desired B 1 distributions only, simplifying SAR management considerably.

The experiments described above demonstrate that C2ONTAR elements can be successfully used for parallel acquisition and parallel excitation and may for certain MRI applications substitute conventional power source-driven transmit and receive elements.