1 Introduction

Nuclear quadrupole resonance (NQR) spectroscopy enables the determination of two relevant quantities: the nuclear quadrupole coupling constant eQq 2 and the asymmetry parameter η of the electric field gradient (EFG) tensor. These quantities provide important information on the distribution of the electron charge density in the molecular system studied. However, for I = 3/2 nuclei the quadrupolar energy levels are double degenerated, so that η cannot be determined from the NQR frequency alone. In recent years, a variety of experimental methods that enable determining eQq 2 and η for I = 3/2 nuclei, without applying an external magnetic field, have been developed. One of these is the method of two-dimensional (2-D) nutation NQR spectroscopy [1, 2]. This technique has been developed further in Refs. [3–15] and has become the most practical and convenient method to determine eQq 2 and η for I = 3/2 nuclei. Simultaneously, for small values of η this method requires the accurate measurement of frequencies of the two adjacent singularities overlapping each other. To increase the resolution of these poorly resolved singularities, the maximum entropy method has been applied with varying success [16, 17], the inhomogeneity of the radio-frequency (rf) field in the sample coil has been taken into account [18], the sample has been melted and polarized in a strong direct current (DC) magnetic field prior to the measurement [19], etc.

The method for determining the asymmetry parameter of the EFG tensor on spin I = 3/2 nuclei is based on recording and analyzing the singularities of the nutation spectra of powder samples. This method has many advantages compared to traditional methods, which require applying a DC magnetic field. However, if the value of η is small, i.e., η < 10%, resolving two closely spaced singularities is often unreliable, especially when one of them appears to be a shoulder rather than a minimum or a maximum. Additionally, the 2-D interferograms have to be accumulated a large number of times to obtain an acceptable signal-to-noise (S/N) ratio, and so it will require a longer time to complete the experiment.

Like other multidimensional spectroscopy methods, the 2-D nutation NQR spectroscopy appears to be a tedious one, where the experiments are often an hour long. The requirements for choosing the proper sampling period in time dimension t w (pulse duration) increase when the value of η to be determined by means of the nutation NQR spectroscopy decreases. Conventionally, N 1-D free induction decay (FID) signals are acquired for nutation pulse length t w incremented by equal steps, Δt w. Then, a 2-D fast Fourier transform (FFT) of the acquired data is performed in time dimensions t (FID time) and t w (nutation pulse duration). Many unconventional methods were proposed in recent years to speed up multidimensional experiments. References to related articles can be found in Ref. [20]. The idea of using random sampling for recording the multidimensional interferograms in nuclear magnetic resonance (NMR) [20] is not new in principle. There are a number of other methods, which have been used in various branches of science, for processing the incomplete, partly lost or inaccessible data.

The present work is aimed at studying the possibility of shortening the time of nutation experiment, without worsening the resolution of frequency singularities by the application of random sampling of experimental data. Our additional goals were to obtain the analytic formulae for complex 2-D nutation NQR spectra (I = 3/2) and to assess the conditions of resolving the singularities in the nutation spectra recorded for small values of η.

2 Theory

The intensity of the NQR FID signal after an rf pulse of duration t w was calculated in Ref. [21] and can be written as

$$ G(t,t_{\text{w}} ) = {\frac{\alpha }{{(3 + \eta^{2} )\xi }}}R^{2} (\theta ,\phi )\sin \xi t_{\text{w}} \{ U\sin [\omega_{0} (t - t_{\text{w}} )] + V\cos [\omega_{0} (t - t_{\text{w}} )]\} , $$
(1)

where

$$ \alpha = {\frac{{\gamma B_{1} }}{4}},\xi = \frac{1}{2}\sqrt {4m^{2} + \Updelta \omega^{2} } ,m = {\frac{\alpha R(\theta ,\phi )}{{\sqrt {3 + \eta^{2} } }}} , $$
$$ R(\theta ,\phi ) = \sqrt {4\eta^{2} \cos^{2} \theta + \sin^{2} \theta (9 + \eta^{2} + 6\eta \cos 2\phi )} , $$
$$ U = \cos \xi t_{\text{w}} \cos \Updelta \omega t_{\text{w}} + {\frac{\Updelta \omega }{2\xi }}\sin \xi t_{\text{w}} \sin \Updelta \omega t_{\text{w}} , $$
$$ V = - \cos \xi t_{\text{w}} \sin \Updelta \omega t_{\text{w}} + {\frac{\Updelta \omega }{2\xi }}\sin \xi t_{\text{w}} \cos \Updelta \omega t_{\text{w}} , $$

Δω = ω − ω0 is the offset of the spectrometer frequency from the NQR frequency, and θ and φ are the polar coordinates of the rf magnetic field in the EFG principal axes system.

If the reference voltage of the phase-sensitive detector takes the form

$$ U_{R} = U_{R0} \begin{array}{*{20}c} {\sin } \\ {\cos } \\ \end{array} \omega t , $$

the complex FID signal on the output will be

$$ G(t,t_{\text{w}} ) \propto {\frac{{m^{2} }}{2\alpha \xi }}\sin \xi t_{\text{w}} \left( {\cos \xi t_{\text{w}} + i{\frac{\Updelta \omega }{2\xi }}\sin \xi t_{\text{w}} } \right)\exp ( - i\Updelta \omega t) , $$
(2)

or taking into account the nutation frequency ωn0 = 2ξ:

$$ G(t,t_{\text{w}} ) \propto {\frac{{m^{2} }}{{2\alpha \omega_{{{\text{n}}0}} }}}\left[ {\sin \omega_{{{\text{n}}0}} t_{\text{w}} + i{\frac{\Updelta \omega }{{\omega_{{{\text{n}}0}} }}}\left( {1 - \cos \omega_{{{\text{n}}0}} t_{\text{w}} } \right)} \right]\exp ( - i\Updelta \omega t). $$
(3)

Taking into consideration the finite width of the NQR line and assuming that the line shape is Gaussian, we multiply Eq. (3) by the factor \( \exp \left[ { - \frac{1}{2}\left( {\sigma^{2} t^{2} + \sigma_{\text{n}}^{2} t_{\text{w}}^{2} } \right)} \right]. \) In addition to this, we take into consideration the fact that due to intrinsic dead time of the NQR spectrometer, the NQR data acquisition does not start immediately after the rf pulse is off but is delayed by t = t 0:

$$ G(t,t_{\text{w}} ) \propto {\frac{{m^{2} }}{{2\alpha \omega_{{{\text{n}}0}} }}}\left[ {\sin \omega_{{{\text{n}}0}} t_{\text{w}} + i{\frac{\Updelta \omega }{{\omega_{{{\text{n}}0}} }}}(1 - \cos \omega_{{{\text{n}}0}} t_{\text{w}} )} \right]\exp [ - i\Updelta \omega (t - t_{0} )]\exp \left\{ { - \frac{1}{2}\left[ {\sigma^{2} (t - t_{0} )^{2} + \sigma_{\text{n}}^{2} t_{\text{w}}^{2} } \right]} \right\}. $$
(4)

After taking a double 2-D FFT of Eq. (4), the 2-D nutation spectrum is obtained as

$$ S(\omega ,\omega_{\text{n}} ) \propto {\frac{{\pi m^{2} }}{{2\alpha \omega_{{{\text{n}}0}}^{2} \sigma \sigma_{\text{n}} }}}e^{i\beta } e^{{ - {\frac{{(\omega + \Updelta \omega )^{2} }}{{2\sigma^{2} }}} - i(\omega + \Updelta \omega )t_{0} }} \left[ \begin{gathered} (\omega_{{{\text{n}}0}} + \Updelta \omega )e^{{ - {\frac{{(\omega_{{{\text{n}}0}} - \omega_{\text{n}} )^{2} }}{{2\sigma_{\text{n}}^{2} }}}}} \hfill \\ - (\omega_{\text{n0}} - \Updelta \omega )e^{{ - {\frac{{(\omega_{{{\text{n}}0}} + \omega_{\text{n}} )^{2} }}{{2\sigma_{\text{n}}^{2} }}}}} \hfill \\ - 2\Updelta \omega e^{{ - {\frac{{\omega_{\text{n}}^{2} }}{{2\sigma_{\text{n}}^{2} }}}}} \hfill \\ \end{gathered} \right] , $$
(5)

where β = Δωt0, the phase that has to be corrected so that pure absorption-like nutation spectrum is obtained

$$ S_{\text{a}} (\omega ,\omega_{\text{n}} ) \propto {\frac{{\pi m^{2} }}{{2\alpha \omega_{{{\text{n}}0}}^{2} \sigma \sigma_{\text{n}} }}}\cos [(\omega + \Updelta \omega )t_{0} ]e^{{ - {\frac{{(\omega + \Updelta \omega )^{2} }}{{2\sigma^{2} }}}}} \left[ \begin{gathered} (\omega_{{{\text{n}}0}} + \Updelta \omega )e^{{ - {\frac{{(\omega_{{{\text{n}}0}} - \omega_{\text{n}} )^{2} }}{{2\sigma_{\text{n}}^{2} }}}}} \hfill \\ - (\omega_{{{\text{n}}0}} - \Updelta \omega )e^{{ - {\frac{{(\omega_{{{\text{n}}0}} + \omega_{\text{n}} )^{2} }}{{2\sigma_{\text{n}}^{2} }}}}} \hfill \\ - 2\Updelta \omega e^{{ - {\frac{{\omega_{\text{n}}^{2} }}{{2\sigma_{\text{n}}^{2} }}}}} \hfill \\ \end{gathered} \right]. $$
(6)

As evident from Eq. (6), a mirror spectrum exists in the ωn dimension which is of an opposite sign to the basic spectrum. In the presence of a frequency offset, the mirror and basic spectra differ in intensity (proportionally to ωn0 ± Δω). The spectrum intensity at the zero nutation frequency ωn = 0 is proportional to the frequency offset Δω.

For powder samples, the formula for the 2-D nutation spectrum has to be averaged over all angles, θ and φ. Figure 1 shows a 1-D nutation spectrum simulated using formula Eq. (6). The spectrum is mirrored around the nutation frequency ωn = 0, and the mirror and basic spectra are inversely phased to each other. The presence of a frequency offset between the NQR and the excitation rf pulse signal leads to shifting of nutation frequencies and changing the shape of nutation spectra (the shape change is more pronounced for the basic spectrum than for the mirror one). Besides, a narrow line appears at the zero frequency of the nutation spectrum and originates due to a DC component in the time domain signal G(t w). The intensity of this line increases with increasing frequency offset, Δω. Baseline correction of the 2-D signal G(ω, t w) is needed to get rid of this spurious line after taking the first Fourier transform of G(t, t w) over t. Phase correction of the G(ω, ωn) nutation spectrum may also be necessary in the ω dimension after taking the second Fourier transform over s w.

Fig. 1
figure 1

Simulated 1-D nutation NQR spectrum for I = 3/2, γB1/2π = 57.7 kHz, η = 0.23; σn = 2π × 0.8 kHz at Δν = 0 (a) and Δν = 30 kHz (b)

Full size image

This is connected with the time lag of data acquisition due to some “dead time” normally observed in an NQR spectrometer after turning the rf pulse off, and also due to possible imperfections of the quadrature detector. Phase error in the ωn dimension is absent in principle, so phase correction in this dimension is not needed.

For zero frequency offset, the frequencies of singularities of the nutation spectrum are given by \( \nu_{2,3} = {\frac{{\nu_{\text{r}} (3 \mp \eta )}}{{2\sqrt {3 + \eta^{2} } }}}, \) where νr = γB1/2π. If the maximum duration of the rf pulse is t w max, then the minimum value of the asymmetry parameter to be determined from the nutation experiment (without taking into consideration the natural width of the NQR line) can be found from the condition:\( \nu_{3} - \nu_{2} = {\frac{{\nu_{\text{r}} \eta_{\min } }}{{\sqrt {3 + \eta_{\min }^{2} } }}} = {\frac{1}{{t_{{{\text{w }}\max }} }}},{\text{thus }}\eta_{\min } = \sqrt {{\frac{3}{{\nu_{\text{r}}^{2} t_{{{\text{w }}\max }}^{2} - 1}}}} . \) Assuming that νrtw max ≫ 1, we obtain

$$ \eta_{\min } = {\frac{\sqrt 3 }{{\nu_{\text{r}} t_{\text{w max}} }}}. $$
(7)

The maximum increment step of the rf pulse duration is limited according to the Nyquist sampling theorem for the maximum frequency observable in a spectrum:

$$ \Updelta t_{{{\text{w }}\max }} = {\frac{1}{{\nu_{3} }}} = {\frac{{2\sqrt {3 + \eta^{2} } }}{{\nu_{\text{r}} (3 + \eta )}}}. $$
(8)

3 Experimental

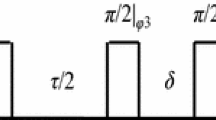
All the 2-D nutation experiments were performed on a pulsed FT NQR spectrometer (0.5–300 MHz) [22]. Powder samples of KClO3, C3Cl3N3, CCl3CH(OH)2 and 2,6-dichloropurine ribonucleoside were studied. The measurements were made at 77 K on chlorine 35Cl nuclei. One- and two-pulse nutation sequences of rf pulses were used. The π/2 pulse duration was 4 μs, the interval between pulses in a spin echo sequence was 70 μs, and the sequence repetition rate varied from 100 to 150 ms. The sampling period for the NQR signal in the t dimension varied from 0.4 to 1.6 μs, depending on the NQR line width. For the acceptable S/N ratio 500–1,000 accumulations of FID or spin echo signals were necessary with receiver bandwidth set to 100 kHz. A complete 2-D nutation experiment lasted from 3 to 17 h, depending on its variant.

For experiments with random sampling, a series of random t w values were generated on a computer as ASCII files, which were then interpreted and executed by a script-driven control software of the NQR spectrometer. The same realizations of random numbers were then used for numerical integration and taking Fourier transform of the NQR data. The maximum value of the nutation pulse duration t w allowable by the NQR spectrometer was 400 μs.

4 Results and Discussion

The tests of possible phase correction of the 2-D nutation NQR spectra and suppression of spurious peaks at zero nutation frequency were performed for the narrow and broad 35Cl-NQR lines with various asymmetry parameters, η. Baseline correction prior to taking second Fourier transform (over t w variable) allowed total suppression of the spurious peak at ωn = 0, and subsequent phase correction made in the ω dimension only yielded a non-distorted absorption spectrum. Figure 2 illustrates the shift of the nutation spectrum along the frequency dimensions ω and ωn and the change in intensities of the basic and mirror nutation spectra when detuning the spectrometer frequency from resonance.

Fig. 2
figure 2

2-D nutation 35Cl-NQR spectrum of KClO3, Δν = 30 kHz, γB1/2π = 45 kHz (FFT of 200 data points uniformly distributed over the pulse duration range t w = 0–320 μs). Spurious peak at zero frequency was removed due to baseline correction that was performed prior to Fourier transform of the nutation interferogram

Full size image

Conventional processing of the 2-D nutation NQR data with FFT algorithms requires that the data points are uniformly distributed on an FID signal. On the one hand, in every dimension the maximum distance between two adjacent data points, according to the Nyquist theorem, cannot exceed the value of the inverse width of the spectrum. If the Nyquist theorem is not obeyed, then spurious signals will appear. On the other hand, the resolution of the nutation spectrum increases with increase in the maximum pulse duration, t w max. As a result, on keeping the number of data points constant, it is not possible to increase the resolution of singularities of nutation spectra without narrowing the observed spectral range.

The method of random sampling in time domain [20] proposed for recording of multidimensional NMR spectra does not allow determining the limit of the observable spectral range. However, it allows increasing the time of observation of the data, and thus increasing the spectral resolution, but without the need for increasing the number of data points.

FID signals G(t, t w) were Fourier transformed for each value of pulse duration t w using a standard fast Fourier transform algorithm: S(ω, t w) = FFT{G (t, t w)}. The integral of Fourier transform over the time variable t w was calculated numerically with the formula

$$ S(\omega ,\omega_{\text{n}} ) = \sum\limits_{{t_{\text{w}} = 0}}^{{t_{\text{w max}} }} {S(\omega ,t_{\text{w}} )\exp ( - i\omega_{\text{n}} t_{\text{w}} )w(t_{\text{w}} )} $$

using the well-known trapezoidal rule. Here w(t w) is the weighting factor that depends on the distribution function of the random variable, t w.

In our experiment, we used a series of random time intervals t w, uniformly distributed over the 0–t w max range, and random numbers with normal distribution \( f(t_{\text{w}} ) = {\frac{1}{{\sigma \sqrt {2\pi } }}}e^{{{\frac{{ - (t_{\text{w}} - \mu )^{2} }}{{2\sigma^{2} }}}}} \) in the same range. For Fourier transform using numerical integration, a preliminary sorting of the data points by values of t w was performed.

The use of random sampling method is accompanied by inherent artifacts and the level of the latter increases with decreasing the number of data points. To increase the number of data points and to make them equidistant, one could, in principle, resort to interpolation of the FID signal with a polynomial. However, the interpolation of periodic functions with polynomials, even of high order, is a rude approximation only and leads also to artifacts that appear to be no less than the aforementioned ones.

As Fig. 3a shows, for uniform sampling at a frequency lower than that required by Nyquist theorem, the nutation spectrum obtained is unacceptably distorted. In this condition, random sampling (Fig. 3b, c) does not distort the nutation spectrum, so it allows to increase t w max. The basic drawback of the random sampling method is the presence of artifacts, which, as well as the sampling itself, are random, depending on the realization of random quantity t w. Besides, the real experimental data usually contain thermal noise and therefore it is advantageous to choose the distribution of random t w intervals so that its maximum density coincides with the FID area where the signal-to-noise ratio is the best.

Fig. 3
figure 3

Simulated 1-D nutation NQR spectrum (numerical integration using trapezoidal rule): a uniform increment, b normal distribution with average μ = 0 and standard deviation σ = 100 μs, c random values with uniform distribution. γB1/2π = 45 kHz, η = 0.23, t w max = 400 μs, 32 data points

Full size image

Figure 4a, b shows the experimental nutation 35Cl-NQR spectra of powder cyanuric chloride C3Cl3N3 obtained respectively by uniform sampling FFT (32 data points in the interval t w = 0–400 μs) and random sampling with normal distribution (32 data points in the interval t w = 0–400 μs). The nutation spectrum in Fig. 4a is distorted because it does not obey the Nyquist theorem, while the spectrum in Fig. 4b obtained for the same number of data points is correct.

Fig. 4
figure 4

Nutation 35Cl-NQR spectrum of C3Cl3N3 recorded at NQR frequency ν = 36.7715 MHz, γB1/2π = 45 kHz, η = 0.23: a numerical integration, 32 data points uniformly distributed over the pulse duration range t w = 0–400 μs; b numerical integration, 32 data points distributed according to normal law with average μ = 0 and standard deviation σ = 100 μs within the pulse duration range t w = 0–400 μs

Full size image

To a greater extent, the presence of artifacts is connected with unequal distances between the data points than with errors in numerical integration. The same method of numerical integration yields good nutation spectra for normal sampling and spectra with artifacts for random sampling. Good results with a minimum level of artifacts can be obtained in the case of oversampling only [23] when the mean relative density of the data points n/(t w max sw n) > 1, where n is the number of data points, and sw n is the width of the nutation spectrum. Increase in oscillation frequency of a nutation interferogram with the increase of amplitude of the rf magnetic field in the presence of detuning from resonance leads to the diminished accuracy of numerical integration and, consequently, to the increased level of artifacts.

5 Conclusions

Analysis of the obtained analytic formulae for a 2-D nutation 35Cl-NQR spectrum and our experiment with powder samples, having different values of η, show that to obtain pure absorption signal, the phase correction of the 2-D nutation NQR spectra is necessary in the ν dimension only; in the nutation frequency dimension νn, such a correction is not needed. From Eq. (7), for the minimum possible value ηmin, which can still be determined, the resolution of spectral singularities is limited by the maximum possible value of the expression γB 1 t w max. The method of random sampling allows reducing the time required for recording the nutation interferogram and does not worsen the resolution of the characteristic singularities of the 2-D nutation NQR spectra.