Alternative forms of buyer power in a vertical duopoly: implications for profits, welfare, and cost pass-through

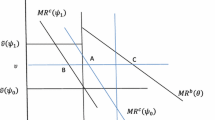
Abstract

We examine the implications of different ways in which downstream firms can exercise buyer power over their upstream suppliers. We derive several variations of a model in which two upstream firms supply a differentiated product under exclusive contracts to two downstream firms which compete in prices in the retail market. We begin with a benchmark model (upstream first-mover pricing), and then compare its outcomes with those of models that feature different modes of exercising buyer power: downstream first-mover pricing; Nash Bargaining with linear and two-part tariffs; and vertical integration. We rank these five regimes in terms of wholesale and retail prices, social welfare, the pass-through rates of changes in upstream costs, and downstream firms’ profits. We show under what conditions more powerful downstream firms benefit consumers by exercising ‘countervailing power’ against upstream suppliers. We also show that the lump-sum component of the two-part tariff can go in either direction (a slotting allowance or a franchise fee), depending in a very precise way only on parameters representing bargaining power and the degree of product differentiation. Exactly the same configuration of these parameters is shown to determine the ranking of wholesale and retail prices, pass-through rates, and downstream profits, as between the Nash Bargaining regimes with linear and two-part tariffs. Finally, we show that downstream firms which possess buyer power always prefer vertical arrangements that are socially sub-optimal.

Appendices

Appendix 1: Derivation of the demand function

Following Singh and Vives (1994), we assume a representative consumer’s utility function as:

$$U\left( {q_{0} ,q_{1} ,q_{2} } \right) = \alpha q_{1} + \alpha q_{2} - \frac{{\beta q_{1}^{2} + \beta q_{2}^{2} + 2\lambda q_{1} q_{2} }}{2} + q_{0}$$

Here q_i is quantity produced by upstream firm i. ${q}_{0}$ is a Hicksian composite commodity consisting of all other goods outside the market of interest. Since we are working with real prices we are normalizing price one unit of this basket equal to 1. We assume $\alpha >0, \beta >0.$ To derive the demand function we maximize this utility function for q₀, q₁ and q₂:

$$\mathop {{\text{max}}}\limits_{{q_{0} ,~q_{1} ,q_{2} }} \left\{ {U\left( {q_{1} ,q_{2} } \right) = \alpha q_{1} + \alpha q_{2} - \frac{{\beta q_{1}^{2} + \beta q_{2}^{2} + 2\lambda q_{1} q_{2} }}{2} + q_{0} } \right\}$$

Subject to the budget constraint:$Y={q}_{0}+{p}_{1}{q}_{1}+{p}_{2}{q}_{2}$

On maximization we get the following inverse demand function

$$p_{1} = \alpha - \beta q_{1} + \lambda q_{2}$$

$$p_{2} = \alpha - \beta q_{2} + \lambda q_{1}$$

On rearranging terms we get direct demand functions as

$${q}_{1}=a-b{p}_{1}+\upgamma {{\text{p}}}_{2}$$

where,

$$a = \alpha \left( {\beta - \lambda } \right)/\delta$$

$$b = \beta /\delta$$

$$\mathrm{\gamma }=\frac{\lambda }{\delta }$$

where $\delta \equiv (\beta ^{2} - \lambda ^{2} )$

• When γ/b approaches 1 it implies $\frac{\gamma }{b} = \frac{{{\uplambda }/{\updelta }}}{{{\upbeta }/{\updelta }}} = \frac{{\uplambda }}{{\upbeta }} \to 1$, which implies that δ$\to 0$, where the demands are undefined. Therefore, we assume γ < b. We have adapted this restriction for the case where b = 1, which is used to derive the results. b = 1 implies $\frac{\beta }{\delta }=1$.

• Most papers in economics journals follow Singh and Vives (1994) by substituting the parameters of the inverse demand function into the a, b and γ parameters of the direct demand function before proceeding with the firms’ profit-maximization exercise. The direct demand specification without substitution was used in the early papers on vertical relationships with downstream competition in prices, e.g. Lin (1990) and O’Brien and Shaffer (1993). It was actually first used by McGuire and Staelin (1983), and continues to be used extensively in the literature on marketing and operations research (although it is not derived from maximizing a utility function). See Wang et al (2016), Li et al (2020) and many other papers cited there. However, it creates a problem of discontinuity as γ/b approaches 1.

• Another problem with using the direct demand specification, which does not seem to have been noticed by earlier authors, is that it gives the same 'monopoly' results when either γ = 0 (signifying independent demands and no competition), or p_j = 0 (signifying intense competition). This can be averted by bounding prices above zero by assuming positive marginal costs, with $\alpha \ge c$, and the upstream firm assumed to have constant marginal cost of production equal to c.

Appendix 2: First order conditions for the Nash Bargaining model with two-part tariff

An upstream firm’s profit can be written as

$${\uppi }_{U1}=\left({w}_{1}-c\right){q}_{1}-{S}_{1}$$

where,

${w}_{1}$: wholesale price.

${S}_{1}$: slotting allowance

Downstream firm’s profit can be written as

$${\uppi }_{D1}=\left({{p}_{1}-w}_{1}\right){q}_{1}+{S}_{1}$$

(16)

Define the Nash product of upstream and downstream profits as:

$$N={\uppi }_{D1}^{ 1-\mu } {\uppi }_{U1}^{ \mu }$$

(17)

On differentiating with respect to S₁, we get

$$\frac{\partial N}{\partial {S}_{1}}=\left(1-\mu \right){\uppi }_{D1}^{ -\mu } {\uppi }_{U1}^{ \mu }+{\left(-\mu \right)\uppi }_{D1}^{ 1-\mu } {\uppi }_{U1}^{ \mu -1}=0$$

(18)

When we solve the above first order condition for ${\uppi }_{D1}$ we get

$$=>\frac{\left(1-\upmu \right){\uppi }_{U1} }{\upmu }={\uppi }_{D1}$$

(19)

When we substitute into equation A4 above the profit function of the upstream and downstream firms, we get below equation

$$\frac{\left(1-\upmu \right) }{\upmu }\left[\left({w}_{1}-c\right){q}_{1}-{S}_{1}\right]=\left({p}_{1}-{w}_{1}\right){q}_{1}+{S}_{1}$$

On rearranging the terms on both sides, we get:

$${{S}}_{1}^{{*}} = \left( {1 - {{\mu}}} \right)\left[ {\left( {{{w}}_{1} - {{c}}} \right){{q}}_{1} } \right] - {{\mu}}\left[ {\left( {{{p}}_{1} - {{w}}_{1} } \right){{q}}_{1} } \right]$$

On differentiating N with respect to wholesale price w, we get

$$\frac{\partial N}{\partial {w}_{1}}=\left(1-\mu \right){\uppi }_{D1}^{ -\mu } {\uppi }_{U1}^{ \mu }\frac{\partial {\uppi }_{D1}}{\partial {w}_{1}}+{\left(\mu \right)\uppi }_{D1}^{ 1-\mu } {\uppi }_{U1}^{ \mu -1}\frac{\partial {\uppi }_{U1}}{\partial {w}_{1}}=0$$

$$=>\frac{\left(1-\upmu \right){\uppi }_{U1} }{\upmu }\frac{\partial {\pi }_{D1}}{\partial {w}_{1}}={-\uppi }_{D1}\frac{\partial {\pi }_{U1}}{\partial {w}_{1}}$$

Substituting equation A4 into the above equation we get

$$\frac{\partial {\pi }_{D1}}{\partial {w}_{1}}+ \frac{\partial {\pi }_{U1}}{\partial {w}_{1}}=0$$

Appendix 3: Proof of Proposition 2

$${p}_{i,VI}^{*}<{p}_{i,NB2}^{*}\lesseqgtr{p}_{i,NB1}^{*}<{p}_{i,FM}^{*}={p}_{i,B}^{*} \, {\text{as}} \, {\gamma }^{2}\lesseqgtr2\mu$$

We have already shown above that prices are the same in the FM and benchmark cases. Now we prove the inequalities successively.

• 1. ${{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}\le {{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}$

  $${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}=\frac{a(2\left(2+\mu \right)-2{\gamma }^{2})-c(2-{\gamma }^{2})(\mu -2)}{(2-\gamma )(4-2{\gamma }^{2}-\gamma \mu )}, {{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}=\frac{a+{\text{c}}}{(2-\upgamma )}$$
  $${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}-{{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}=\frac{a\left(2\left(2+\mu \right)-2{\gamma }^{2}\right)-c\left(2-{\gamma }^{2}\right)\left(\mu -2\right)}{\left(2-\gamma \right)\left(4-2{\gamma }^{2}-\gamma \mu \right)}- \frac{a+{\text{c}}}{(2-\upgamma )}$$
  $$=\frac{(a+c(-1+\gamma ))(2+\gamma )\mu }{(2-\gamma )(4-2{\gamma }^{2}-\gamma \mu )}\ge 0, \, \mathrm{with equality for} \, \mu =0$$

In the above expression, in the numerator $\left(a+c\left(-1+\gamma \right)\right)>0$ by Lemma 1, and ($2+\gamma )>0$. So, the numerator is positive. In the denominator, $\left(2-\gamma \right)>0$ and $\left(4-2{\gamma }^{2}-\gamma \mu \right)>0$ for all values of $\gamma {\text{and}} \mu$ in the given ranges. Thus, ${{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}\le {{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}$, with the vertically integrated outcome emerging when downstream firms have all bargaining power, as explained in the text.

• 2. ${{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}\le {{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}$

  $${\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} = \frac{{2a + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right) }}, {\text{p}}_{{{\text{i}},{\text{VI}}}}^{*} = \frac{a + c}{{\left( {2 - \gamma } \right)}}$$
  $${\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} - {\text{p}}_{{{\text{i}},{\text{VI}}}}^{*} = \frac{{2a + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right) }} - \frac{a + c}{{\left( {2 - \gamma } \right)}}$$

  $= \frac{{\gamma^{2} \left( {a - \left( {1 - \gamma } \right)c} \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma - \gamma^{2} } \right) }} \ge 0$, with equality for $\gamma <0$

The denominator here is positive, as $\left(2-\upgamma \right)>0, \left(4{-2\upgamma }^{2}-\upgamma \right)>0$. In the numerator, $\left(a-\left(1-\upgamma \right)c\right)>0$ and ${\upgamma }^{2}\ge 0$ for all values of γ between 0 and 1. This shows that ${{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}$≤${{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}$ holds true for all relevant values of $\upgamma$ and c. Once again, the vertical integration outcome emerges when goods are independent.

• 3. ${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}\lesseqgtr{{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*} \, {\text{as}} \, 2\mu \lesseqgtr{\gamma }^{2}$

  $${\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} = \frac{{2a - c\left( {\gamma^{2} - 2} \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right) }}, {\text{p}}_{{{\text{i}},{\text{NB}}1}}^{*} = \frac{{a\left( {2\left( {2 + \mu } \right) - 2\gamma^{2} } \right) + c\left( {2 - \gamma^{2} } \right)\left( {2 - \mu } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma \mu } \right)}}$$
  $$\begin{gathered} {\text{p}}_{{{\text{i}},{\text{NB}}1}}^{*} - {\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} = \frac{{a\left( {2\left( {2 + \mu } \right) - 2\gamma^{2} } \right) + c\left( {2 - \gamma^{2} } \right)\left( {2 - \mu } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma \mu } \right)}} - \frac{{2a + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right)}} \hfill \\ = \frac{{2\left( {a + c\left( { - 1 + \gamma } \right)} \right)\left( {2 - \gamma^{2} } \right)\left( {\gamma^{2} - 2\mu } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma - \gamma^{2} } \right)\left( { - 4 + 2\gamma^{2} + \gamma \mu } \right)}} \hfill \\ \end{gathered}$$

Note that $\left(a+c\left(-1+\gamma \right)\right)>0$ by Lemma 1; the second term in the numerator and the first two terms in the denominator are also positive; but the last term in the denominator is strictly negative. So the sign of the entire expression will be the opposite of the sign of ${(\gamma }^{2}-2\mu )$, which determined the sign of S* in Proposition 1. Not surprisingly, therefore, when $\frac{(2-{\gamma }^{2})({\gamma }^{2}-2\mu )}{(2-\gamma )(4-2\gamma -{\gamma }^{2})(-4+2{\gamma }^{2}+\gamma \mu )}$ is plotted in Mathematica software, the region for which ${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}>{{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}$ turns out to be identical to the zone consistent with a franchise fee (unshaded region) in Fig. 2.

• 4. ${p}_{i,NB1}^{*}\le {p}_{i,FM}^{*}$, with equality for $\mu$=1.

  $${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}=\frac{a\left(2\left(2+\mu \right)-2{\gamma }^{2}\right)+c\left(2-{\gamma }^{2}\right)\left(2-\mu \right)}{\left(2-\gamma \right)\left(4-2{\gamma }^{2}-\gamma \mu \right)}$$
  $${{\text{p}}}_{{\text{i}},{\text{FM}}}^{*}= \frac{6a-2a{\upgamma }^{2}+c({2-\upgamma }^{2})}{(4-2{\upgamma }^{2}-\upgamma )(2-\upgamma )}$$
  $$\begin{aligned} {\text{p}}_{{{\text{i}},{\text{FM}}}}^{*} - {\text{p}}_{{{\text{i}},{\text{NB}}1}}^{*} & = \frac{{6a - 2a\gamma ^{2} + c\left( {2 - \gamma ^{2} } \right)}}{{\left( {4 - 2\gamma ^{2} - \gamma } \right)\left( {2 - \gamma } \right)}} \\ & \quad - \frac{{a\left( {2\left( {2 + \mu } \right) - 2\gamma ^{2} } \right) + c\left( {2 - \gamma ^{2} } \right)\left( {2 - \mu } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma ^{2} - \gamma \mu } \right)}} \\ & = \frac{{2\left( {a - \left( {1 - \gamma } \right)c} \right)\left( {2 + \gamma } \right)\left( {2 - \gamma ^{2} } \right)\left( {1 - \mu } \right)}}{{\left( {2 - \gamma } \right)\left( {2\gamma ^{2} + \gamma - 4} \right)\left( {2\gamma ^{2} + \gamma \mu - 4} \right)}} \\ \end{aligned}$$

In the numerator $\left(a-\left(1-\gamma \right)c\right)>0$ by Lemma 1, $\left(1-\mu \right)\ge 0$, $\left({2-\gamma }^{2}\right)>0$. So, the numerator is positive. In the denominator, $\left(2-\gamma \right)>0$, $\left(2{\gamma }^{2}+\gamma -4\right)<0$ and $\left(2{\gamma }^{2}+\gamma \mu -4\right)<0$ for all values of $\gamma$ and μ in the relevant ranges (the last two expressions are non-factorizable and checked in Mathematica for the direction of their signs). Thus, ${{\text{p}}}_{{\text{i}},{\text{FM}}}^{*}\ge {{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}.$

• 5. ${{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}<{{\text{p}}}_{{\text{i}},{\text{FM}}}^{*}$

  $${\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} = \frac{{2a + c\left( {2 - \gamma^{2} } \right) }}{{\left( {4 - 2\gamma - \gamma^{2} } \right) }};\quad {\text{p}}_{{{\text{i}},{\text{FM}}}}^{*} = \frac{{6a - 2a\gamma^{2} + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)}}$$
  $$\begin{aligned} {\text{p}}_{{{\text{i}},{\text{FM}}}}^{*} - {\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} &= \frac{{6a - 2a\gamma^{2} + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)}} - \frac{{2a + c\left( {2 - \gamma^{2} } \right) }}{{\left( {4 - 2\gamma - \gamma^{2} } \right)}} \hfill \\ &= \frac{{2\left( {2 - \gamma^{2} } \right)^{2} \left( {a - \left( {1 - \gamma } \right)c} \right)}}{{\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)\left( {4 - 2\gamma - \gamma^{2} } \right)}} > 0 \hfill \\ \end{aligned}$$

All three terms in both the numerator and denominator are strictly positive for all values of γ between 0 and 1.

Combining results 1–5 and excluding the polar cases for μ and γ proves Proposition 2, which gives us a ranking of retail prices across the five regimes.

Appendix 4: Binary comparisons of wholesale prices

• 1. ${{w}_{i,B}^{*}\ge w}_{i,NB1}^{*}$, with equality for $\mu$ = 1.

  $$\begin{aligned} w_{i,B}^{*} - w_{i,NB1}^{*} & = \frac{{a\left( {2 + \gamma } \right) - c\left( {\gamma^{2} - 2} \right)}}{{4 - 2\gamma^{2} - \gamma }} - \frac{{a\left( {2 + \gamma } \right)\mu + c\left( {\gamma^{2} - 2} \right)\left( {\mu - 2} \right)}}{{2\left( {2 - \gamma^{2} } \right) - \gamma \mu }} \\ & = \frac{{2\left( {a + c\left( { - 1 + \gamma } \right)} \right)\left( {2 + \gamma } \right)\left( {2 - \gamma^{2} } \right)\left( {1 - \mu } \right)}}{{\left( {4 - \gamma - 2\gamma^{2} } \right)\left( {4 - 2\gamma^{2} - \gamma \mu } \right)}} \\ \end{aligned}$$

For $0\le \mu$ < 1, all terms in the numerator and denominator are positive; while for $\mu =1$ the numerator is zero. Hence proved.

• 2. ${w}_{i,FM}^{*}>{w}_{i,NB2}^{*}$

  $${w}_{i,FM}^{*}-{w}_{i,NB2}^{*}=\frac{a\left(2-{\gamma }^{2}\right)+c(6-4\gamma -2{\gamma }^{2}+{\gamma }^{3})}{(2-\gamma )(4-2{\gamma }^{2}-\gamma )}-\frac{{a\gamma }^{2}+c\left(({2-\gamma }^{2})(2-\gamma )\right)}{\left(4-2\gamma -{\gamma }^{2}\right)}$$
  $${w}_{i,FM}^{*}-{w}_{i,NB2}^{*}=\frac{2\left(4-2\gamma -7{\gamma }^{2}+4{\gamma }^{3}+2{\gamma }^{4}-{\gamma }^{5}\right)\left(a-\left(1-\gamma \right)c\right)}{(2-\gamma )(4-2{\gamma }^{2}-\gamma )\left(4-2\gamma -{\gamma }^{2}\right)}$$

All three terms in the denominator of the above expression are positive for $\gamma <1$. In the numerator, $\left(a-\left(1-\upgamma \right)c\right)>0$ (Lemma 1), and the expression $4-2\upgamma -7{\upgamma }^{2}+4{\upgamma }^{3}+2{\upgamma }^{4}-{\upgamma }^{5}$ can be factorized to $(1-\upgamma )(4+2\upgamma -5{\upgamma }^{2}-{\upgamma }^{3}+{\upgamma }^{4})$ which is positive for all values of $\gamma$ between 0 and 1. Hence proved.

Finally, amongst the five vertical regimes, it is obvious that wholesale price will be lowest for vertical integration, as firms maximize their integrated profit behaving as single entity, setting wholesale price equal to the upstream marginal costs. From Table 1 and our earlier discussion, the NB1 regime gives the same outcome when μ = 0, corresponding to what we described as “wholesale price maintenance” when the downstream firm has all the bargaining power and can extract the entire channel profit. Along with Lemma 2, and excluding the polar cases for μ and γ, these results rule out all except the three orderings in the text, on the basis of which we proved Proposition 3.

Appendix 5: Binary comparisons of downstream profits

• 1. Comparing downstream profits from Vertical integration and Nash Bargaining contract with two-part tariff:

  $$\begin{aligned} \pi_{{{1},{\text{NB2}}}}^{{{\text{D}}*}} - \pi_{{{1},{\text{VI}}}}^{{{\text{D}}*}} & = \frac{{2(1 - \gamma )(2 - \gamma^{2} )(a - c(1 - \gamma ))^{2} }}{{(4 - \gamma^{2} - 2\gamma )^{2} }} - \frac{{(1 - \gamma )(a - c + \gamma c)^{2} }}{{(2 - \gamma )^{2} }} \\ & = \frac{{\gamma^{3} \left( {1 - \mu } \right)\left( {4 - 3\gamma } \right)\left( {a - c\left( {1 - \gamma } \right)} \right)^{2} }}{{\left( {4 - \gamma^{2} - 2\gamma } \right)^{2} \left( {2 - \gamma } \right)^{2} }} \ge 0,\;{\text{with}}\;{\text{equality}}\;{\text{for}}\;\gamma \;{\text{or}}\;\mu \, = \,{1} \\ \end{aligned}$$

For μ < 1 and γ strictly between 0 and 1, both the numerator and denominator of the above expression are positive.

• 2. Comparing profits from First-mover pricing model and Linear Pricing (benchmark) model

This result was already implied by our earlier finding that the only difference between the two regimes is that wholesale prices are lower, and therefore downstream margins are higher, in the FM case. However, this can be confirmed explicitly by comparing the profit expressions as follows:

$$\begin{aligned} \pi_{{{1},{\text{FM}}}}^{{{\text{D}}*}} - \pi_{{{1},{\text{B}}}}^{{{\text{D}}*}} &= \frac{{\left( {a - c + c\gamma } \right)^{2} \left( {2 - {\upgamma }^{2} } \right)\left( {2 + {\upgamma }} \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} }} - \frac{{\left( {2 - {\upgamma }^{2} } \right)^{2} \left( {a + \left( {{\upgamma } - 1} \right)c} \right)^{2} }}{{\left( {\left( {4 - 2{\upgamma }^{2} - {\upgamma }} \right)\left( {2 - {\upgamma }} \right)} \right)^{2} }} \hfill \\ &= \frac{{2\left( {2 - {\upgamma }^{2} } \right)\left( {{\text{a}} - c\left( {1 - {\upgamma }} \right)} \right)^{2} }}{{\left( {4 - 2{\upgamma }^{2} - {\upgamma }} \right)^{2} \left( {2 - {\upgamma }} \right)^{2} }} > 0 \hfill \\ \end{aligned}$$

All the terms in both the numerator and denominator of this expression are positive for all values of $\upgamma$ between 0 and 1.

• 3. Comparing profits from Nash Bargaining with two-part tariff and Linear Pricing (benchmark),

  $$\begin{aligned} \pi_{{{1},{\text{NB2}}}}^{{^{{{\text{D}}*}} }} &= \frac{{2\left( {1 - } \right)\left( {2 -^{2} } \right)\left( {a - c\left( {1 - } \right)} \right)^{2} }}{{\left( {4 -^{2} - 2} \right)^{2} }} - \frac{{\left( {2 -^{2} } \right)^{2} \left( {a + \left( { - 1} \right)c} \right)^{2} }}{{\left( {\left( {4 - 2^{2} - } \right)\left( {2 - } \right)} \right)^{2} }} \hfill \\ &= \frac{{\left( {^{2} - 2} \right)\left( {a - c\left( {1 - } \right)} \right)^{2} \left( {2\left( { - 1} \right)\left( {\left( {4 - 2^{2} - } \right)\left( {2 - } \right)} \right)^{2} - \left( {^{2} - 2} \right)\left( {4 -^{2} - 2} \right)^{2} } \right)}}{{\left( {4 - 2^{2} - } \right)^{2} \left( {2 - } \right)^{2} \left( {4 -^{2} - 2} \right)^{2} }} > 0 \hfill \\ \end{aligned}$$

The denominator of the above expression is positive as all the terms are squared. In the numerator, $\left(a-\left(1-\upgamma \right)c\right)>0 ;\left({\upgamma }^{2}-2\right)<0$ for all values of $\gamma$ between 0 and 1. The expression $\left(2\left(\upmu -1\right){\left(\left(4-2{\upgamma }^{2}-\upgamma \right)\left(2-\upgamma \right)\right)}^{2}-\left({\upgamma }^{2}-2\right){\left(4-{\upgamma }^{2}-2\upgamma \right)}^{2}\right)$ can be shown by numerical simulation to be negative for all relevant values of $\mu$ and $\gamma .$ This shows that π_1,NB2^D* > π_1,B^D* holds true for all relevant values of $\gamma , \mu$ and c.¹⁶ The two-part tariff enables each chain to maximize its combined profit, and downstream firms with more bargaining power benefit from this.

• 4. Comparing profits from vertical integration and downstream first-mover model:

  $$\begin{aligned} \pi_{{{1},{\text{VI}}}}^{{{\text{D}}*}} - \pi_{{{1},{\text{FM}}}}^{{{\text{D}}*}} & = \frac{{\left( {1 - \mu } \right)\left( {a - c + \gamma c} \right)^{2} }}{{\left( { - 2 + \gamma } \right)^{2} }} - \frac{{\left( {a - c + c\gamma } \right)^{2} \left( {2 - \gamma^{2} } \right)\left( {2 + \gamma } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} }} \\ & = \frac{{\left( {a - c + \gamma c} \right)^{2} }}{{\left( {2 - \gamma } \right)^{2} \left( {4 - 2\gamma^{2} - \gamma } \right)^{2} }}\left[ {\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} \left( {1 - {\upmu }} \right) - \left( {2 - {\upgamma }^{2} } \right)\left( {4 - {\upgamma }^{2} } \right)} \right] \\ \end{aligned}$$

All the expressions are squared, except the one in square brackets. If we plot this expression $[\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} \left( {1 - {\upmu }} \right) - \left( {2 - {\upgamma }^{2} } \right)\left( {4 - {\upgamma }^{2} } \right)]$ in (μ, γ) space we get Fig. 5. 

Fig. 5

Values of $\gamma$ and $\mu$ for which (π_1,VI^D*, π_2,VI^D*) > (π_1,FM^D*, π_2,FM^D*)

• 5. Comparing profits from downstream first-mover contract and Nash Bargaining contract with a two-part tariff, i.e.,

  $$\begin{aligned} {\uppi }_{{1,{\text{NB}}2}}^{{\text{D*}}} - {\uppi }_{{1,{\text{FM}}}}^{{\text{D*}}} & = \frac{{2\left( {1 - \mu } \right)\left( {2 - \gamma^{2} } \right)\left( {a - c\left( {1 - \gamma } \right)} \right)^{2} }}{{\left( {4 - \gamma^{2} - 2\gamma } \right)^{2} }} \\ & \quad - \frac{{\left( {a - c + c\gamma } \right)^{2} \left( {2 - \gamma^{2} } \right)\left( {2 + \gamma } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} }} \\ & = \left( {2 - {\upgamma }^{2} } \right)\left( {a - c\left( {1 - {\upgamma }} \right)} \right)^{2} \left( {\frac{{2\left( {1 - {\upmu }} \right)}}{{\left( {4 - {\upgamma }^{2} - 2{\upgamma }} \right)^{2} }} - \frac{{\left( {2 + {\upgamma }} \right)}}{{\left( {2 - {\upgamma }} \right)\left( {4 - 2{\upgamma }^{2} - {\upgamma }} \right)^{2} }}} \right) \\ \end{aligned}$$

We can plot $\left(\frac{2(1-\upmu )}{{\left(4-{\upgamma }^{2}-2\upgamma \right)}^{2}}-\frac{\left(2+\upgamma \right)}{\left(2-\gamma \right){\left(4-2{\gamma }^{2}-\gamma \right)}^{2}}\right)$ in $(\mu , \gamma )$ space to get Fig. 6. 

Fig. 6

Values of $\gamma$ and $\mu$ for which (π_1,FM^D*, π_2,FM^D*) < (π_1,NB2^D*, π_2,NB2^D*)

• 6. Comparing profits from Vertical Integration and Benchmark models i.e.,

  $$\begin{aligned} {\uppi }_{{1,{\text{VI}}}}^{{\text{D*}}} - {\uppi }_{{1,{\text{B}}}}^{{\text{D*}}} & = \frac{{\left( {1 - \mu } \right)\left( {a - c + \gamma c} \right)^{2} }}{{\left( {2 - \gamma } \right)^{2} }} - \frac{{\left( {2 - \gamma^{2} } \right)^{2} \left( {a + \left( {\gamma - 1} \right)c} \right)^{2} }}{{\left( {\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)} \right)^{2} }} \\ & = \frac{{\left( {a + \left( {\gamma - 1} \right)c} \right)^{2} \left( {\left( {1 - \mu } \right)\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} - \left( {2 - \gamma^{2} } \right)^{2} } \right)}}{{\left( {\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)} \right)^{2} }} \\ \end{aligned}$$

If we plot $\left((1-\upmu \right){\left(4-2{\upgamma }^{2}-\upgamma \right)}^{2}-{\left(2-{\upgamma }^{2}\right)}^{2})$ in (μ, γ) space we get Fig. 7. 

Fig. 7

Values of $\upgamma$ and $\mu$ for which (π_1,VI^D*, π_2,VI^D*) > (π_1,B^D*, π_2,B^D*)