Brand premia driven by perceived vertical differentiation in markets with information disparity and optimistic consumers

Abstract

We have considered a duopoly with perceived vertical differentiation, information disparity and optimistic consumers. When firms compete for informed and uninformed consumers, the former contribute to raise product quality, while equilibrium prices increase with optimistic misperception of the latter, in our first equilibrium. Brand premium includes a quality premium and a misperception rent. In our second equilibrium, informed consumers buy low-quality goods and minimum product differentiation without Bertrand competition occurs. The brand premium is just a misperception rent, however, an increase of the informed consumers share implies price re-balancing and rent reduction. Consumers externalities arise in both equilibria. Firms compete only for informed consumers within our third and fourth equilibrium, as uninformed ones are passive and represent a captive market. Uninformed consumers in one case are overoptimistic, they buy the high quality good and can be cheated in equilibrium. Uninformed consumers approach the real quality differential in the fourth equilibrium, and the model reduces to standard vertical differentiation with perfect information.

1 Introduction

Brand loyalty is traditionally considered a vehicle of product differentiation (Cabral 2017). Though brand loyalty may also arise for products of superior quality, sold at higher prices justified by quality premia, perceived quality differences in many cases establish a vertical distance between products. To the best of our knowledge, models of perceived vertical differentiation have been overlooked in economic literature¹. Contributions by Tremblay and Martins Filho (2001), and Tremblay and Polasky (2002) are an exception. They focus on persuasive advertising to induce brand loyalty with the effect of either enhancing or generating a vertical distance between products. Tremblay and Polasky (2002) point out that firms can avoid Bertrand Competition by investing in persuasive advertising, even in markets where products are close substitutes.

A more recent empirical study by Bronnenberg et al. (2015) introduces a new approach by comparing sales of ’National brands’ and ’Store brands’ in the US², aiming to evaluate the welfare effects of brand loyalty in markets where identical products are sold at different prices³. The authors emphasize the purchasing behavior of informed and uninformed consumers to explain the formation of brand premia concerning both health and certain food products.

Informed consumers are purchasers who can name the active ingredients in goods. Consumers’ information is driven either by higher education or expertise due to occupation in a specific sector (physicians or pharmacists in the domain of health products). Therefore, education is a proxy of information, and information turns out to be indirectly correlated with income, as education is also determined by it. The results show that informed consumers are more likely to buy generics than brands and allow to conclude that misinformation and product quality overrating explain brand premia for many health products, as well as for certain food.

In our contribution, we have highlighted information disparity and quality misperception as a brand premia driver, like in Bronnenberg’s study (2015), but we have also aimed to carry out a theoretical analysis by introducing consumers’ misperception into a vertical differentiation model with heterogeneous consumers. We have distinguished perceived from real vertical differentiation, and we have investigated to what extent brand premia are real quality ones, or just misperception rents. Brands will be generally identified with (perceived or real) high-quality products and generics with low-quality ones.

We have analyzed a two-stage duopoly model, where real product quality is endogenously chosen by the high-quality firm. Equilibrium analysis includes both cases: when firms really increase product quality, and when brand premia are just driven by quality misperception without any quality improvement. Furthermore, this model allows us to consider a case where the brand premium includes both a quality premium and a misperception rent. We have investigated cases where most consumers are uninformed, and cases where they could be either informed or uninformed. The first type of equilibrium is also examined in Bronnenberg et al. (2015), but differently from them, we have introduced the respective shares of informed and uninformed consumers in the model explicitly, analyzing the effects of the share changes on equilibrium prices and product quality.

Our model is characterized by multiple sources of consumers’ heterogeneity. Here information disparity is added to income inequality. Moreover, uninformed consumers have biased beliefs concerning high-quality products. Because of their optimistic misperception, uninformed consumers overestimate the quality differential provided by brands. Our analysis can, indeed, be included in the field of behavioral industrial organization (Ellison 2006), where there is general consensus about the assumption of profit maximization for firms that respond strategically to biased consumers’ beliefs.

Most of these contributions consider the case of price misperception⁴, however, as highlighted by Heidhues and Kozsegi (2018), quality misperception mainly generates the same effect: consumers overestimate the value of their purchase, and firms make extra-profits. Experimental evidence has shown that economic agents may systematically hold incorrect beliefs, because of what psychologists broadly define overconfidence (Einhorn and Hogarth 1978), referring to excess optimism or overconfidence about the precision of their own information.⁵

According to Muthukrishnan (2015), overconfidence can also explain brand loyalty to the extent that additional experience with the same product can strengthen biased beliefs without any further learning. Regret avoidance may be an additional explanation. Originally introduced by Loomes and Sugden (1982), it has been reconsidered in the framework of brand loyalty by Muthukrishnan (2015). In his opinion, persistent preference for the same product appears to be a risk reduction strategy, due to the fact that uncertainty about the quality of other options may be accompanied by the prospect of perceived regret in case of product failure.

A further feature of our model is that uninformed consumers with biased beliefs, and informed purchasers are not randomly distributed in the market. As higher education and willingness to pay for quality are both positively correlated with income, information disparity closely follows the distribution of willingness to pay for quality⁶. Therefore, the higher the willingness to pay for quality, the higher the likelihood a consumer is informed, as information distribution overlaps the uniform distribution of willingness to pay, given the common correlation with income. For example, consumers with higher income and education are likely to be better informed about product quality, implying they might purchase a generic product. On the contrary, less educated uninformed consumers with lower income perceive the branded good as a higher quality one.

The share of informed and uninformed consumers in our model is exogenously given. However, we are interested in analyzing quality and price competition for the entire range of information disparity. The latter gives rise to different shares of informed and uninformed consumers separated by the threshold value of the willingness to pay, and emerging in the model according to alternative parameter restrictions. Equilibrium restrictions concerning the threshold value in the first two cases allow to specify the extension of the informed and uninformed consumers’ shares, and whether one share prevails.

Duopolistic competition with (perceived or real) vertical differentiation is represented as usual with a two-stage game: firms choose the quality level in the first stage, given an exogenous split between informed and uninformed consumers affecting market demand. Price competition takes place in the second stage.

We have considered two types of equilibria for the case in which most consumers are uninformed with firms competing both for uninformed and informed consumers, and two additional equilibria, where firms focus only on the informed ones, as the uninformed purchasers are passive and represent a captive market.

We have shown that it is optimal for a low-quality firm to minimize quality level in any equilibrium. However, we assume the government has introduced a minimum quality standard to avoid quality deterioration, so that firms have to comply with it. On the contrary, the quality level chosen by a high-quality company is totally endogenous and drives the real quality differential in equilibrium.

When most consumers are uninformed, equilibrium prices increase, compared to the full information benchmark, reflecting the quality differential expected by optimistic consumers. As high quality products, in this case, are also bought by informed consumers, even a low share of them is sufficient to induce an increase of the quality level chosen by the high-quality firm. Moreover, a growing share of informed consumers represents an incentive for a high-quality firm to raise product quality, as any increase in the expected quality differential does. This is exactly the case where the brand premium can be analytically separated into a quality premium and a misperception rent. Informed consumers in our second equilibrium buy low quality goods as uninformed consumers with the lowest willingness to pay. Higher quality claims are only exploiting uninformed consumers’ optimistic misperception, as in equilibrium both firms just comply with the minimum quality standard, and, therefore, we can observe minimum product differentiation. However, the Bertrand Paradox does not follow⁷, because such an optimistic misperception, and the informed consumers’ share drive equilibrium prices. In this equilibrium, the brand premium is just a misperception rent and can be potentially reduced with an increase of informed consumers.

We have then considered two further equilibria, where firms compete only for informed consumers. The uninformed ones in the third equilibrium are overoptimistic and result to be ’passive’ with respect to competition, representing a sort of ’captive market’ for a high-quality firm. When some of them become informed, they switch to low-quality goods, inducing the high-quality firm to reduce price and quality levels. Therefore, increasing the informed consumers’ share does not benefit product differentiation. Moreover, we have noticed that the remaining share of uninformed consumers perceives as a bargain what, in fact, is a rip-off (Armstrong 2015)

Uninformed consumers in a fourth equilibrium buy low-quality goods, behaving as if they were quasi-informed, making the same choice of informed consumers located next to them. Actually, despite the persistence of information disparity, the model, in this case, reduces to standard vertical differentiation with perfect information. For each equilibrium but the last one, we have referred to examples of real markets that seem to fit with our theoretical conclusion.

This paper is structured as follows: we will discuss the relevant literature in Sect. 2 and present the basic model in Sect. 3; we will then outline the methodology employed to obtain demand functions in Sect. 4. As for equilibrium analysis, we will consider the case without information disparity, where choice is only affected by optimistic misperception as a benchmark in Sects. 5, 6 will analyze equilibria with information disparity, when most consumers are uninformed, and Sect. 7 will examine equilibria, where firms compete only for informed consumers, while Sect. 8 represents our conclusion.

2 The former literature

The analysis of markets with information disparity concerning product quality is not new in economic literature. According to Chan and Leland (1982), Cooper and Ross (1984), and Wolinsky (1983), informed consumers can exert a positive externality on the uninformed ones, as long as the incentive to supply higher quality products depends on the informed consumers’ share. In this framework, with perfect or monopolistic competition consumers have rational expectations, and higher prices may signal higher quality goods. Further contributions, by Stahl (1989) and Moraga-Gonzalez et al. (2017) focused on search costs, or on experience-good trials (Villas-Boas 2006) and underlined the importance of consumer heterogeneity to understand market frictions in an oligopoly.

Our study of information disparity departs from the previous contributions, firstly because we have introduced uninformed consumers with biased beliefs, and secondly with reference to market structure assumptions, as we have considered a duopoly with vertically differentiated products. New contributions in the field of behavioral industrial organization (Heidhues and Kozsegi 2018), accounting for biased beliefs, obtained ambiguous results as to the effects of the informed consumers’ share on the welfare of the uninformed ones. Armstrong’s analysis (2015) sheds more light on this ambiguity by introducing the distinction between models where ’savvy’ consumers benefit ’unsavvy’ ones, and models where either informed consumers are subsidized by those with biased beliefs, or there is no interaction between the two groups. Our paper brings forth new results concerning the effects of consumer heterogeneity, consistent with the distinction made by Armstrong, as we have detected consumers’ externalities in the first two equilibria, while there is no interaction between informed and uninformed consumers in the third and fourth equilibrium.

A further question regards the type of products that can be relevant for our analysis. The previous literature about consumer heterogeneity has considered search goods and experience goods, though (Wolinsky 1983) product quality concerning the latter either included some random component, or purchases were so infrequent to prevent the reputation mechanism from working effectively.

If products are credence goods, as in the case of drugs and other health products, chemicals or green goods, there are ’hidden characteristics’, and most consumers may lack the expertise to ascertain quality differentials, even after purchase⁸. Reputation, in this setting, may not be an effective mechanism to convey information about product quality, as proven by experimental evidence (Dulleck et al. 2011). Therefore, quality misperception and information disparity may be even more relevant for goods with credence characteristics. However, assuming biased consumers’ beliefs, quality misperception can be a driver of brand premia for experience goods, as well.

Information disparity among consumers in a duopoly with vertical differentiation was first introduced by Cavaliere (2005), who considered only price competition. Here we are going to extend our analysis to quality choice, when producing higher quality goods requires a costlier effort. Also Garella and Petrakis (2008) evaluated information disparity, consumers’ misperception, and endogenous quality, but in an oligopolistic setting with imperfect substitutes, according to the Dixit-Spence approach. Gabszewicz and Resende, (2012) analyzed vertical differentiation referred to credence goods without considering quality choice. Brouhle and Khanna (2007) examined vertical differentiation and imperfect information with endogenous quality, although consumer heterogeneity normally depends on beliefs concerning the accuracy of information provision.

3 The basic model

We have considered a market with a consumers’ continuum. The willingness to pay for quality $\theta$ (wtp from now on) is uniformly distributed between ${\theta }$ and $\bar{\theta }$ with $\bar{\theta }= \underline{\theta }+1$, and density $f(\theta )=1$. Each consumer buys one unit of a product (assuming the market is completely covered). Consumer preferences can be represented by the following quasi-linear utility function (Mussa and Rosen 1978):

$$U = \theta q_{i} - P_{i} \;\;{\text{i = L}},{\text{H}}$$

(1)

where P is the market price and q represents product quality, which can be low $(q_{L})$ or high $(q_{H})$⁹. There is a Minimum Quality Standard (MQS) $q_{0}$ enforced by the government in order to prevent quality deterioration; $q_{0}$ is common knowledge. Actually consumers expect that the government will control product quality, requiring products to comply with safety and effectiveness standards. Consumers have rational expectations about low-quality products, as they anticipate that $q_{L}=q_{0}$ (such expectation is fulfilled in equilibrium)¹⁰.

High quality $q_{H}$ can vary in the range: $q_{0}\le q_{H}\le q_{H}^{Max},$ where $q_{H}^{Max}$ is the maximum level of feasible quality that a firm can achieve with the current technology. This high-quality level is perfectly known to producers but unknown to consumers, unless they are included in the informed consumers’ (IC from now on) share. Uninformed consumers (UC from now on) are not able to check higher quality claims. They can just exclude that $q_{H}<q_{0}$ and hold quality expectation $q_{E}$ about high-quality products. UC are not even informed about $q_{H}^{Max},$ and, consequently, we cannot exclude that $q_{E}$ $\ge q_{H}^{Max}$.

The model can deal with any quality misperception, as UC either believe that $q_{E}>$ $q_{H}$, or that $q_{E}<$ $q_{H}$. We have concentrated on the case where $q_{E}>$ $q_{H},$ i.e. UC are characterized by optimistic misperception¹¹. Though $q_{E}$ could be different among consumers, for the sake of simplicity and tractability within a vertically differentiated duopoly, we have considered a single $q_{E}$ that could be identified as the average quality UC expect. As far as real markets are concerned, what matters is that firms are able to identify $q_{E}$. Actually firms, differently from consumers, can hire consultants, do market research, use big data, and, moreover, they are active in one or just a few markets (DellaVigna 2009)¹².

As to the distinction between IC and UC, we have split the market according to the distribution of $\theta$, by introducing a cut-off value $\theta ^{*}$. Consumers with wtp for quality $\theta \ge \theta ^{*}$ are informed about $q_{H}$. Consumers with wtp $\theta <\theta ^{*}$ remain uninformed and make purchase decisions on the basis of optimistic expectations $q_{E}>q_{H}$. Therefore, the greater $\theta ^{*}$ is, the lower the IC share $(1-\theta ^{*})$. The value of $\theta ^{*}$ does not need any restriction, except that $\underline{\theta }$ $<\theta ^{*}\le$ $\bar{\theta }$.

Furthermore, it is important to point out that our model implies that the higher the wtp for quality is, the more likely it is for a consumer to be informed. Greater wtp is correlated with higher income, but higher income is also positively associated with superior education, which is a proxy for quality information. Such an assumption implies that any consumer j with wtp $\theta _{j}>$ $\theta _{i}$ will be informed if a consumer i with wtp $\theta _{i}$ is, i.e. $\theta _{i}>\theta ^{*}$. Therefore, richer consumers are more likely to be included in the IC share. They may decide to buy a low-quality good, despite their higher income, when it is not worthwhile to pay a brand premium, because quality is not really as superior as UC expect¹³.

We shall suppose that there are two firms in the market which can produce either a product of $q_{L}$ or of $q_{H}$ quality. The product of quality $q_{L}$ can be identified with a generic, and the product of quality $q_{H}$ (be it real or perceived) with the brand. Firm one will specialize in the production of quality $q_{L}$, and firm two in the production of quality $q_{H}$ in order to avoid the problem of multiple equilibria. We will label firm one as L , and firm two as H. We shall not consider fixed production costs, as we have disregarded the entry stage, and we shall normalize the variable production costs to zero. Supposing that higher quality production implies greater efforts, we shall establish the cost of quality as $\alpha q_{i}^{2}$, $i=L,H$, with $\alpha q_{L}^{2}<\alpha q_{H}^{2}.$ For example, we can imagine cases where firms must respect a MQS but can put more stress on quality control, which improves product quality.

Low-quality goods are sold at price $P_{L}$, and the high-quality ones at price $P_{H}$. As we assume that the market is fully covered, we suppose that, in equilibrium, $P_{L}^{*}\le q_{L}\underline{\theta }$ if we take for granted that the consumer with the lowest wtp will buy a $q_{L}$ product. As there is also one case in our model where this same consumer can buy a high-quality product, because of an overoptimistic expectation $q_{E}$ , we need to set $P_{H}^{*}\le q_{E}\underline{\theta }.$

The timing structure of the model can be described as follows:

• 1. In the first stage, the market is split between UC and IC, according to their heterogeneity regarding $\theta$, which is exogenously given, and to the location of the cut-off value $\theta ^{*}$; UC quality expectations are also exogenously given;

• 2. In the second stage, firms taking consumers’ information and expectations about the quality differential as given, choose their quality level;

• 3. In the third stage, firms compete in prices.

4 Market demands

In order to identify market demands, we will start from the definition of the marginal consumer for whom it is indifferent to buy from firm L or H . Actually IC in our model are able to evaluate the real quality $q_{H},$ while UC just have expectations $q_{E}$. Both kinds of consumers presume that $q_{L}=q_{0}$. Therefore, we need to define two types of marginal consumers. The first one is the uninformed marginal consumer $\theta ^{\prime }$ with optimistic misperception who is defined by the following equality: $\theta ^{\prime }q_{0}-P_{L}=\theta ^{\prime }q_{E}-P_{H}$ giving:

$$\begin{aligned} \theta ^{\prime }=\frac{P_{H}-P_{L}}{q_{E}-q_{0}} \end{aligned}$$

(2)

Let us call $\Delta _{E}=q_{E}-q_{0}$ the expected quality differential. Consequently, UC with willingness to pay $\theta \ge \theta ^{\prime }$ (and $\theta \le \theta ^{*}$) will choose a high-quality product, whereas UC with willingness to pay $\theta <\theta ^{\prime }$ (and $\theta <\theta ^{*}$) will select a low-quality one.

The second marginal consumer is the informed one $\theta ^{\prime \prime }$:

$$\begin{aligned} \theta ^{\prime \prime }=\frac{P_{H}-P_{L}}{q_{H}-q_{0}} \end{aligned}$$

(3)

being $\Delta =q_{H}-q_{0}$ the real quality differential. Thus IC with willingness to pay $\theta \ge \theta ^{\prime \prime }$ (and $\theta \ge \theta ^{*}$) pick a high-quality product, while IC with wtp $\theta \le \theta ^{\prime \prime }$(and $\theta \ge \theta ^{*}$) decide on a low-quality one.

However, definition of the demand functions requires further assumptions regarding the parameters of the model. For each market division between IC and UC, i.e. for each location of the cut-off value $\theta ^{*},$market demands can change according to the location of $\theta ^{\prime }$ and $\theta ^{\prime \prime }$. When considering the relative locations of the marginal consumers $\theta ^{\prime }$ and $\theta ^{\prime \prime }$ within the market, we are necessarily led to identify two main cases: either $\theta ^{\prime }<\theta ^{\prime \prime }$ or $\theta ^{\prime }>\theta ^{\prime \prime }$. Given $P_{H},\,P_{L}$ , and $q_{0}$, the sign of the previous inequality only depends on the relationship between $q_{E}$ and $q_{H}$. As mentioned above, we have kept to the case of optimistic misperception, and we, therefore, assume $\ q_{E}>q_{H}$ implying $\theta ^{\prime }<\theta ^{\prime \prime }$.

Demand functions are given by the following general expression:

$$\begin{aligned} D_{i}(P_{L},P_{H},\Delta _{E},\Delta ,\theta ^{*});i=L,H \end{aligned}$$

To specify market demands (from now on $D_{L}$ and $D_{H}$), we then need to consider alternative parameter restrictions concerning the location of $\theta ^{*}$ in space $\left[ \underline{\theta },\bar{\theta }\right] ,$ compared to the $\theta ^{\prime }$ and $\theta ^{\prime \prime }$ones in this same space. Each parameter restriction gives rise to different market demands, and, consequently, equilibria will be analyzed accordingly.

5 Equilibrium analysis with consumers’ misperception but without information disparity

Firstly, we shall present a benchmark case with no information disparity, where all consumers are uninformed and affected by quality misperception. Actually, this benchmark case simply derives from our previous model, restricted to consider only the uninformed marginal consumer $\theta ^{\prime }$ and defines demand functions as: $D_{L}\left( P_{L},P_{H},\Delta _{E}\right) =\left( \theta ^{\prime }- \underline{\theta }\right)$ and $D_{H}\left( P_{L},P_{H},\Delta _{E}\right) =\left( \bar{\theta }-\theta ^{\prime }\right)$ implying the following profit functions:

$$\begin{aligned} \Pi _{L}\left( P_{L},P_{H}\right) =P_{L}\left( \theta ^{\prime }- \underline{\theta }\right) -\alpha q_{L}^{2}\qquad \Pi _{H}\left( P_{L},P_{H}\right) =P_{H}\left( \bar{\theta }-\theta ^{\prime }\right) -\alpha q_{H}^{2} \end{aligned}$$

(4)

Equilibrium prices depend on the expected quality differential $\Delta _{E}$:

$$\begin{aligned} P_{L}^{*}=\frac{\Delta _{E}\left( \bar{\theta }-2 \underline{\theta }\right) }{3}\qquad P_{H}^{*}=\frac{\Delta _{E}\left( 2\bar{\theta }- \underline{\theta }\right) }{3} \end{aligned}$$

(5)

Price competition is further relaxed by misperceived quality differentiation, due to the fact that equilibrium prices are higher compared to the standard model of vertical differentiation without quality misperception we referred to¹⁴, as $\Delta _{E}>$ $\Delta$.

Because $q_{H}$ is costlier to produce compared to $q_{L},$ while the real quality differential $\Delta$ cannot be observed by consumers, it is optimal both for firm L and firm H to minimize the quality level and produce $q_{H}^{*}=q_{L}^{*}=q_{0}$. Therefore, we can notice minimum product differentiation in equilibrium, i.e. $\Delta =0$. Consequently, firms obtain the following profits in the Subgame Perfect Nash Equilibrium (SPNE):

$$\begin{aligned} \Pi _{L}^{**}=\frac{\Delta _{E}\left( \bar{\theta }-2 \underline{\theta }\right) ^{2}}{9}-\alpha (q_{0})^{2}\qquad \Pi _{H}^{**}=\frac{\Delta _{E}\left( 2\bar{\theta }- \underline{\theta }\right) ^{2}}{9}-\alpha (q_{0})^{2} \end{aligned}$$

(6)

We can define the brand premium as the difference between the profits of firm H and the ones of firm L:

$$\begin{aligned} \Pi _{H}^{*}-\Pi _{L}^{*}=\frac{\Delta _{E}\left( 1+2 \underline{\theta }\right) }{3} \end{aligned}$$

Brand premium is linked to what we define a ’misperception rent’ (Iossa and Palumbo 2010) $\Delta _{E}=\left( q_{E}-q_{0}\right)$ , and to the fact that firm H can impose a higher price, as $\left( P_{H}^{*}-P_{L}^{*}\right) =(2 \underline{\theta }+1)$ , because in the SPNE, $\Delta ^{*}=(q_{H}^{*}-q_{0})=0,$ there is no quality premium in the benchmark case, and the brand premium is only due to consumers’ misperception.

6 Equilibrium analysis with information disparity where most consumers are uninformed

We will now carry out an equilibrium analysis with information disparity. In this section, we shall focus on two cases, where the UC share is greater than the IC one, and firms compete both for IC and UC. Moreover, IC in the first equilibrium buy brands, while in the second one only generics. The complete specification of demand functions for these two cases has been reported in “Appendix 1”, whereas the detailed proofs about quality choice are included in “Appendix 2”.

6.1 Product differentiation sustained by informed consumers

The first case results from the following parameter restriction:

$$\begin{aligned} \left( \underline{\theta }\le \theta ^{\prime }\le \theta ^{\prime \prime }\le \theta ^{*}\le \bar{\theta }\right) \end{aligned}$$

(7)

implying the subsequent price domains for demand functions:

$$\begin{array}{*{20}l} {P_{H} - \theta ^{*} \Delta \le P_{L} \le P_{H} - \underline{\theta } \Delta _{E} } \hfill \\ {P_{L} + \underline{\theta } \Delta _{E} \le P_{H} \le P_{L} + \theta ^{*} \Delta } \hfill \\ \end{array}$$

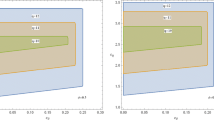
What is particular about this parameter restriction (see Fig. 1) is that the informed marginal consumer $\theta ^{\prime \prime }$ is uninfluential in the UC range: $\underline{\theta }\le \theta ^{\prime }\le \theta ^{*}$ , where $\theta ^{\prime }$ determines demand segments. Therefore, the restriction applies with $\underline{\theta }\le \theta ^{\prime }\le \theta ^{*}=\theta ^{\prime \prime }$, so that any consumer with a $\theta$ included in the range $\theta ^{*}=\theta ^{\prime \prime }\le \theta \le \bar{\theta }$ will choose a high-quality good. We can derive utility functions for UC and IC depending on the type of purchased good, and, consequently, demand segments as in Fig. 1.

Fig. 1

Utility functions and demand segments

Demand segments are obtained from utility maximization. $D_{L}$ depends only on UC in this case: $D_{L}=(\theta ^{\prime }-$ $\underline{\theta })$ , while $D_{H}$ is determined by the UC segment: $(\theta ^{*}-\theta ^{\prime }),$ and by the IC one: $(\bar{\theta }-\theta ^{*})$. By summing up the two of them the result is: $D_{H}=\left( \bar{\theta }-\theta ^{\prime }\right)$.

Demand segments imply that some UC are going to buy $q_{L}$, and the remaining ones $q_{H},$ whereas all the IC are going to purchase $q_{H}$. However, demand functions depend only on $\theta ^{\prime },$ i.e on $\Delta _{E}$ (see “Appendix 1”).

Proposition 1

When most consumers are uninformed, IC buy $q_{H}$ and firms compete both for UC and IC, equilibrium prices are driven by $\Delta _{E}$. The optimal quality chosen by firm H increases with the IC share and with $\Delta _{E}$. Yet, in equilibrium, the real quality differential $\Delta ^{*}$never attains $\Delta _{E}$.

The proof concerning equilibrium prices easily follows: on the basis of $D_{L}$ and $D_{H}$, we can define the following profit functions:

$$\begin{aligned} \Pi _{L}\left( P_{L},P_{H},\Delta _{E}\right) =P_{L}\left( \theta ^{\prime }- \underline{\theta }\right) -\alpha q_{L}^{2}\qquad \Pi _{H}\left( P_{L},P_{H},\Delta _{E}\right) =P_{H}\left( \bar{\theta }-\theta ^{\prime }\right) -\alpha q_{H}^{2} \end{aligned}$$

(8)

By backward induction, we can compute equilibrium prices:

$$\begin{aligned} P_{L}^{*}=\frac{\Delta _{E}\left( \bar{\theta }-2 \underline{\theta }\right) }{3}\qquad P_{H}^{*}=\frac{\Delta _{E}\left( 2\bar{\theta }- \underline{\theta }\right) }{3} \end{aligned}$$

(9)

By checking if equilibrium prices are included in the price domains of the demand functions, we can derive an equilibrium restriction on the UC share as: $\theta ^{*}\ge \frac{\Delta _{E}\left( 2 { \theta }+1\right) }{3\Delta }$. This restriction is consistent with most consumers being uniformed, because $\theta ^{*}>(1-$ $\theta ^{*}),$ i.e. $\frac{\Delta _{E}\left( 2 \underline{\theta }+1\right) }{ 3\Delta }>(1-\frac{\Delta _{E}\left( 2 \underline{\theta } +1\right) }{3\Delta }),$ reducing to the following inequality: $2 \frac{\Delta _{E}}{\Delta }>1$ , which always holds with optimistic consumers. QED

It can be noticed that price competition is further reduced compared to the standard case of vertical differentiation with perfect information, due to higher equilibrium prices, depending on $\Delta _{E}$ $>\Delta$.

By backward induction, we can consider the choice of optimal quality levels, given equilibrium profits obtained in the final stage game. It is optimal for firm L to minimize $q_{L}$, but it needs to stick to the MQS $q_{L}=q_{0}$. Concerning firm H, even the existence of an IC minority represents an incentive to differentiate its products and choose the minimum quality level $q_{H}^{*}$ consistent with the IC share purchasing a high-quality product. The complete proof can be checked in “Appendix 2”, where we have derived the optimal quality level for firm H:

$$\begin{aligned} q_{H}^{*}=q_{0}+\frac{\Delta _{E}\left( 2 \underline{\theta } +1\right) }{3\theta ^{*}} \end{aligned}$$

(10)

Therefore, $q_{H}^{*}>q_{0}$ , and the real quality differential $\Delta ^{*}$ $=\left( q_{H}^{*}-q_{0}\right)$ imply product differentiation. Looking at the expression of $q_{H}^{*}$, we can point out that it increases with $\Delta _{E}$ , and with a decrease of $\theta ^{*}$, i.e. with the growth of the IC share $\left( 1-\theta ^{*}\right)$. As to the first effect, we can notice that more and more optimistic expectations, leading to a rise of $q_{E}$, involve an increase of equilibrium prices. The latter needs to be matched to $q_{H}^{*}$ growth, in order to keep up the incentive for IC to buy high-quality goods. As far as the the second effect is concerned, firm H has to raise quality in order not to deceive those UC that have become informed and are still buying from firm H.

All consumers end up paying excessive prices in equilibrium. As $\Delta ^{*}<\Delta _{E}$ the growth of $q_{H}^{*}$ above $q_{0}$ is never sufficient to match UC optimistic expectations. However, expansion of the IC share exerts a positive externality on the share of UC that buy $q_{H}$, as far as the choice of $q_{H}^{*}$ is concerned. On the contrary, the existence of UC purchasing high- quality goods, causes a negative externality on IC , because $P_{H}^{*}$ increases with $\Delta _{E}$. As to buyers of low-quality goods, any rise of $\Delta _{E}$ also leads to expand $P_{L}^{*}$, due to duopolistic competition between strategic complements, with a disadvantage for these consumers, because firm L will continue to choose $q_{L}=q_{0}$ despite the price augmentation.

Result 2

The brand premium depends on $\Delta _{E},$ and on the difference in equilibrium prices. An increasing (decreasing) share of IC and a higher (lower) cost of the quality effort decrease (increase) the brand premium.

Considering profits in the SPNE:

$$\begin{aligned} \Pi _{L}^{**}=\frac{\Delta _{E}\left( \bar{\theta }-2 \underline{\theta }\right) ^{2}}{9}-\alpha (q_{0})^{2}\qquad \Pi _{H}^{*+}=\frac{\Delta _{E}\left( 2\bar{\theta }- \underline{\theta }\right) ^{2}}{9}-\alpha (q_{H}^{*})^{2} \end{aligned}$$

(11)

We can compute the brand premium $bp^{1}=\left( \Pi _{H}^{**}-\Pi _{L}^{**}\right)$, becoming after substitution of $q_{H}^{*}$:

$$\begin{aligned} bp^{1}=\frac{\Delta _{E}(1+2 \underline{\theta })(3\theta ^{*2}-\alpha \Delta _{E}(1+2 \underline{\theta }))}{9\theta ^{*2}} \end{aligned}$$

(12)

The brand premium depends on $\Delta _{E}$ , and on the difference between equilibrium prices $(1+2 \underline{\theta })$, like in the case without information disparity (Sect. 5). However, the brand premium in the current case is also affected by $\theta ^{*}$ and $\alpha$. As can easily be checked: $\frac{d\left( bp^{1}\right) }{d\theta ^{*}}>0$ and $\frac{d\left( bp^{1}\right) }{d\alpha }<0.$Therefore, the brand premium rises with an increase of UC, i.e. a decrease of the IC share $\left( 1-\theta ^{*}\right)$, and is reduced by growth of the quality effort costs QED.

Let us consider the former effect. Actually, as firm H needs to provide a real quality differential $\Delta ^{*}$ because of the existence of IC, a lower IC share implies that firm H can choose lower levels of $q_{H}^{*}$ with a cost saving raising the brand premium. This effect occurs when the position of $\theta ^{*}$ moves closer to $\bar{\theta }$ towards consumers with higher and higher wtp, who need a lower $\Delta ^{*}$to keep buying from firm H, while both IC and UC will continue to pay the same equilibrium price $P_{H}^{*}$ , which depends on $\Delta _{E}.$As to the second effect, we can just notice that the quality premium reduces with an increase of the effort cost necessary to provide higher quality goods.

Corollary 3

The Brand Premium includes a quality premium and a misperception rent.

We shall provide an intuitive proof of corollary 3. Both equilibrium prices and quality chosen by firm H augment with $\Delta _{E}$ . However, $\Delta ^{*}$never attains $\Delta _{E}$. Consequently, the brand premium must include a quality premium dependent on $\Delta ^{*},$ but the latter cannot exhaust the brand premium itself, which, in fact, depends on $\Delta _{E}$. Therefore, the difference $(\Delta _{E}-\Delta ^{*})=(q_{E}-q_{H}^{*})$ drives the part of the brand premium beyond the quality premium and is equivalent to the misperception rent. QED

We believe that there can be various product markets fitting with this case. High quality brands of food, like wine and coffee, for example, are chosen by a minority of savvy consumers, motivated by a real quality gap. However, the excessive price difference we register in real markets can go beyond quality premium, as it also reflects the price that unsavvy consumers are ready to pay, just because they have optimistic expectations regarding the brand. The market for luxury cars, or mobile phones offers other examples where we can observe very high prices for well-known brands. Here too, the price difference among competitors is partly justified by a real quality advantage recognized by savvy consumers, though brand premium goes beyond that, including misperception rents derived from overconfident UC, but also paid by purchasers aware of the actual quality gap.

6.2 Minimum product differentiation without Bertrand competition

Let us consider an alternative restriction on the parameters of the model:

$$\begin{aligned} \left( \underline{\theta }\le \theta ^{\prime }\le \theta ^{*}\le \bar{\theta }<\theta ^{\prime \prime }\right) \end{aligned}$$

(13)

When $\theta ^{\prime \prime }>\bar{\theta }$, the informed marginal consumer $\theta ^{\prime \prime }$ is out of the market range and does not affect the definition of demand functions. Therefore, the previous restriction can be reduced to $\left( \underline{\theta }\le \theta ^{\prime }\le \theta ^{*}\le \bar{\theta }\right)$, as shown in Fig. 2. We can define the price domains of the demand functions accordingly:

$$\begin{aligned} P_{H}-\theta ^{*}\Delta _{E}\le & {} P_{L}\le P_{H}- \underline{\theta }\Delta _{E}\text { }; \\ P_{L}+ \underline{\theta }\Delta _{E}\le & {} P_{H}\le P_{L}+\theta ^{*}\Delta _{E}\text { } \end{aligned}$$

Fig. 2

Utility functions and demand segments

Actually all consumers with higher wtp included in the range $\theta ^{*}\le \theta \le \bar{\theta }$ are IC, and for each one of them $\theta<$ $\theta ^{\prime \prime }$, so that every IC will choose $q_{L}$. Their demand is $\left( \bar{\theta }-\theta ^{*}\right)$. Given the location of $\theta ^{\prime }$, $q_{L}$ is also bought by consumers with the lowest wtp, placed in the market segment $\left( \theta ^{\prime }- \underline{\theta }\right)$. Hence by summing the two segments, we obtain:

$$\begin{aligned} D_{L}=\left( \bar{\theta }-\theta ^{*}+\theta ^{\prime }- \underline{\theta }\right) =\left( 1-\theta ^{*}+\theta ^{\prime }\right) \end{aligned}$$

(14)

As shown in Fig. 2, the demand for $q_{H}$ is due to UC with ‘intermediate’ wtp:

$$\begin{aligned} D_{H}=\left( \theta ^{*}-\theta ^{\prime }\right) \end{aligned}$$

(15)

Consequently, $q_{H}$ is bought because of optimistic misperception, and $q_{L}$ is purchased either by consumers with the highest wtp, due to their superior information, or by UC with the lowest wtp, who cannot afford $q_{H}.$ “Appendix 1” reports complete specification of demand functions.

Proposition 4

When most consumers are uninformed, IC buy $q_{L}$ , and firms compete both for IC and UC; equilibrium prices are driven by $\Delta _{E}$ and depend asymmetrically on $\theta ^{*}$. Therefore, when the IC share increases (decreases), $P_{L}^{*}$ decreases (increases), and $P_{H}^{*}$ raises (diminishes). As the optimal quality choice is $q_{0}$ both for firm L and firm H, we reach minimum product differentiation in equilibrium.

Proof

By backward induction, we obtain the following equilibrium prices:

$$\begin{aligned} P_{L}^{*}=\frac{\Delta _{E}\left( 2-\theta ^{*}\right) }{3}\qquad P_{H}^{*}=\frac{\Delta _{E}\left( 1+\theta *\right) }{3} \end{aligned}$$

(16)

As equilibrium prices must be included in the price domains of the demand functions, we can derive the following equilibrium restriction on $\theta ^{*}$: $\theta ^{*}\ge \frac{1}{2}+\frac{3 \underline{\theta }}{2}$, implying that the UC size exceeds 50% of the market. Thus we have a majority of UC in this case, like in the previous one, and equilibrium prices still depend on $\Delta _{E}$. In addition, these prices are asymmetrically affected by changes in $\theta ^{*}$ within the boundaries of the equilibrium restrictions. Consequently, an IC increase exerts a positive externality on UC buying $q_{H}$, who will pay lower prices, and a negative externality on the ones purchasing $q_{L}$ at higher prices. An IC reduction causes the opposite effect. QED

Examining the quality selection stage (see “Appendix 2” for a complete proof), as far as $q_{L}$ is concerned, quality minimization still holds, and compliance with the MQS implies $q_{L}^{*}=q_{0}$. In relation to $q_{H},$ considering that higher quality requires a greater effort cost, and that firm H in this specific equilibrium only sells to UC, firm H also decides to minimize quality level and comply with the MQS: $q_{H}^{*}=q_{0}$. Therefore, we obtain minimum product differentiation in equilibrium. However, the Bertrand Paradox does not occur, because equilibrium prices depend symmetrically on $\Delta _{E},$ and asymmetrically on $\theta ^{*}.$Opposite adjustments of $P_{H}^{*}$ and $P_{L}^{*}$ , due to an increase in $\theta ^{*},$ could neverindicate convergence of equilibrium prices towards $P_{H}^{*}$ $=$ $P_{L}^{*}$, as the latter implies $\theta ^{*}=1/2$, a case that must be excluded because of the equilibrium restriction on $\theta ^{*}$.

Result 5

The Brand Premium $bp^{2}$is a misperception rent and reduces (increases) with an increase (a decrease) of the IC share.

Profits in the SPNE will be given by:

$$\begin{aligned} \Pi _{L}^{**}=\frac{\Delta _{E}\left( 2-\theta ^{*}\right) ^{2}}{ 9}-\alpha q_{0}^{2}\qquad \Pi _{H}^{**}=\frac{\Delta _{E}\left( 1+\theta ^{*}\right) ^{2}}{9}-\alpha q_{0}^{2} \end{aligned}$$

(17)

and computing the brand premium $bp^{2}$

$$\begin{aligned} bp^{2}=\left( \Pi _{H}^{**}-\Pi _{L}^{**}\right) =\frac{ \Delta _{E}(2\theta ^{*}-1)}{3} \end{aligned}$$

(18)

we can see that $bp^{2}$ is identical to the difference in equilibrium prices. As the latter depends on $\Delta _{E},$ and in the SPNE $\Delta ^{*}=0$, there is no quality premium, and the brand premium is just a misperception rent. We can also notice that the brand premium shrinks (grows) with an increase (a decrease) of the IC share $\left( 1-\theta ^{*}\right)$, as in the previous equilibrium. QED

This second equilibrium fits in well with the example of the market for drugs sold over the counter, also quoted by Bronnenberg et al. (2015), as generics are mostly bought by informed consumers who recognize their equivalence to branded products. UC, on the contrary, believe that brands are therapeutically superior to generics and are ready to pay for a brand premium, which is just a misperception rent, because in reality brands and generic drugs are therapeutically equivalent. Nevertheless, certain UC will buy generics if they cannot afford the more expensive brand because of their very low income.

7 Competition for informed consumers and segregation of the uninformed ones

In this section, we shall take two further cases into account: where UC are left aside as a ’captive’ market for firms, and, consequently, firms compete only for IC¹⁵. The latter can buy either high quality or low quality goods. As a result, there is no interaction between UC and IC. Furthermore, the two equilibria can be distinguished according to the degree of optimism among UC.

7.1 Overoptimistic consumers

Let us consider the following parameter restriction: $\left( \theta ^{\prime }\le \underline{\theta }\le \theta ^{*}\le \theta ^{\prime \prime }\le \bar{\theta }\right)$. What is particular about this case is that $\theta ^{\prime }$ is located out of the market range. Therefore, even UC with the lowest wtp will choose to purchase a high-quality good, as in the range $\theta ^{\prime }\le \underline{\theta }\le \theta ^{*}$ , for any $\theta$ we have $\theta >\theta ^{\prime }$. This is due to overoptimistic expectations concerning the high-quality product that can, indeed, compensate for the low wtp of consumers located in this range and induce them to buy $q_{H}$.

Fig. 3

Utility functions and demand segments

As can also be noticed in Fig. 3, if $\theta ^{\prime }$ is located out of the market range, there must be a large difference between $q_{E}$ and $q_{H}$ (the two slopes of the utility functions for UC and IC both buying from firm H). By observing Fig. 3 and considering the following price domains of market demands,

$$\begin{aligned} &\text {for }D_{L}:P_{H}- \underline{\theta }\Delta _{E}\le P_{L}\le P_{H}-\theta ^{*}\Delta \ \\& \text {for }D_{H}:P_{L}+\theta ^{*}\Delta \le P_{H}\le P_{L}+ \underline{\theta }\Delta _{E} \end{aligned}$$

we can derive demand functions:

$$\begin{aligned} D_{L}=(\theta ^{\prime \prime }-\theta ^{*}) \end{aligned}$$

(19)

$$\begin{aligned} D_{H}=\left( \bar{\theta }-\theta ^{\prime \prime }+\theta ^{*}- \underline{\theta }\right) =(1-\theta ^{\prime \prime }+\theta ^{*}) \end{aligned}$$

(20)

Therefore, $D_{L}$ is provided by a portion of the IC share, including consumers with intermediate wtp, while $D_{H}$ is composed by the IC residual demand (consumers with the highest wtp) plus the demand coming from overoptimistic consumers.

Proposition 6

When UC with the lowest wtp buy $q_{H}$ , being overoptimistic, they give rise to a captive market for firm H. Consequently , firm L can only contend IC to firm H, as IC buy both $q_{H}$ and $q_{L}$. Equilibrium prices (1) are driven by the real quality differentiale, because firms compete only for IC; (2) depend asymmetrically on $\theta ^{*}$. The optimal quality level $q_{H}^{*}$ is determined by $\theta ^{*}$as well, and an increase (decrease) in the IC share leads to less (more) product differentiation.

Proof

By backward induction, we can derive the following equilibrium prices:

$$\begin{aligned} P_{L}^{*}=\frac{\Delta \left( 1-\theta ^{*}\right) }{3}\qquad P_{H}^{*}=\frac{\Delta \left( 2+\theta *\right) }{3} \end{aligned}$$

(21)

Equilibrium prices are lower in this case, as they depend on $\Delta <\Delta _{E}$. They are also determined by the IC share through $\theta ^{*}$, like in the previous equilibrium setting. Consequently, increasing the IC share $(1-$ $\theta ^{*})$ leads to reduction of $P_{H}^{*}$, and to growth of $P_{L}^{*}$. Again, it is easy to check that $P_{H}^{*}=P_{L}^{*}$ can be excluded (unless $\Delta =0,$ which is out of the equilibrium, as well). QED

It is interesting to point out that growth of the IC share by default reduces the demand of firm H due to overoptimistic UC. When these consumers become informed, they switch to $q_{L}$; therefore, firm H competes more aggressively by reducing $P_{H}^{*}$ in order to acquire IC from firm L, whose price has increased. Actually UC appear to be ‘passive’ consumers of $q_{H}$, unless they become informed. On the other hand, firms need to compete in price and quality to extend their market share deriving from IC that purchase both high and low quality products.

By checking if equilibrium prices are included in the price domains of demand functions, we obtain the following equilibrium restriction on $\theta ^{*}$:

$$\begin{aligned} \theta ^{*}\le min\left\{ 1\,,\,\frac{3 \underline{\theta } \Delta _{E}}{2\Delta }-\frac{1}{2}\right\} \end{aligned}$$

(22)

In addition, a restriction concerning $q_{E}$ follows:

$$\begin{aligned} q_{E}\ge q_{0}+\frac{\Delta \left( 2\theta ^{*}+1\right) }{3 \underline{\theta }} \end{aligned}$$

(23)

which can be reduced to this inequality:

$$\begin{aligned} \frac{\Delta _{E}}{\Delta }\ge \frac{\left( 2\theta ^{*}+1\right) }{3 \underline{\theta }} \end{aligned}$$

(24)

This last restriction implies that UC need to be optimistic enough to purchase high-quality goods, as stated above. It can be shown that the first restriction is not sufficient to determine if either UC or IC prevail in the market. Actually both cases are consistent with the current equilibrium, unless we introduce further restrictions on the other parameters of the model.

The quality choice is analyzed in detail in “Appendix 2”. Here we can report the usual result for firm L, $q_{L}^{*}=q_{0}$ , and the optimal quality level for firm H :

$$\begin{aligned} q_{H}^{*}=\frac{\theta ^{*^{2}}+4\theta ^{*}+4}{18\alpha } \end{aligned}$$

(25)

Beyond noticing that $q_{H}^{*}$ obviously decreases with an increase of the coefficient $\alpha$ of the effort cost function, what is interesting to point out is that growth of the IC share, i.e. reduction of $\theta ^{*}$, implies a drop of $q_{H}^{*}$. Therefore, a greater IC share reduces product differentiation, i.e. the real quality differential $\Delta ^{*}$.

In fact, as a direct effect of the decrease of $\theta ^{*}$, we can observe a contraction of $D_{H}$ related to overoptimistic UC, because those that become informed switch to $D_{L}.$However, the reduction of $\theta ^{*}$ also implies a further effect on market demand, as an increasing IC share involves a change in equilibrium prices in the second stage, which is anticipated in the first stage. Therefore, firm H foreseeing the reduction of $P_{H}^{*}$ (and the rise of $P_{L}^{*}$ ) strategically exploits the opportunity to attract the portion of IC previously buying from firm L. To make this strategy profitable, firm H also needs to reduce the level of $q_{H}^{*}$. Indeed, the IC that previously bought from firm L will be attracted, being able to afford a high quality product at a lower price, while also the IC with greater wtp, already purchasing $q_{H}$, will continue to buy from firm H, even though $q_{H}$ has been reduced, because they can benefit from a lower $P_{H}^{*}$.

Corollary 7

In case of an increase of the IC share, the remaining share of passive UC benefits from a reduction of $P_{H}^{*}$. As they are not aware that such a price decrease implies a reduction of $q_{H}^{*},$ they perceive as a bargain what is actually a ’ripoff’.

UC perception is that of a bargain when they can purchase a high-quality product at a lower price. However, given the same price, they would switch to a low-quality product if they were informed about $\Delta ^{*}$.

Result 8

The brand premium $bp^{3}$is a quality premium

Let us consider firm profits in the SPNE:

$$\begin{aligned} \Pi _{L}^{**}=\frac{\Delta ^{*}\left( 1-\theta ^{*}\right) ^{2}}{9}-\alpha (q_0 )^{2}\qquad \Pi _{H}^{**}=\frac{\Delta ^{*}\left( 2+\theta ^{*}\right) ^{2}}{9}-\alpha (q_{H}^{*})^{2} \end{aligned}$$

(26)

The brand premium $bp^{3}$in this case depends on the real quality differential $\Delta ^{*}$:

$$\begin{aligned} bp^{3}=\Pi _{H}^{**}-\Pi _{L}^{**}=\frac{\Delta ^{*}(1+2\theta ^{*})}{3}+\alpha [(q_0 )^{2}-(q_{H}^{*})^{2}] \end{aligned}$$

(27)

It is equivalent to the difference in equilibrium prices, net of the effort cost increase, resulting from producing high-quality instead of low-quality goods. QED

In our opinion, the markets for financial activities can be a good example for this case, to the extent that financial markets offer increasingly differentiated and sophisticated solutions for savings allocation, though not suitable for most individuals, for whom standardized solutions may be more appropriate. In addition, these markets provide an example of a clear-cut separation between unsavvy and savvy purchasers. Actually a high number of people are notoriously affected by financial illiteracy, a widespread characteristic among low-income and less educated individuals, in particular (Lusardi and Mitchell 2015), which is consistent with our model. A relevant share of these individuals are often overconfident about their financial knowledge and more likely to incur losses due to wrong choices. Despite regulations and supervision of the financial authorities, uninformed subjects could invest in financial activities not suitable for their risk profile, or avoid risk diversification by concentrating their savings in just one financial product. Financial illiteracy, in the worst cases, may even lead them to fall prey to financial scams¹⁶.

Informed individuals, on the contrary, from a broker’s point of view, represent a completely different market, where less wealthy individuals could profit from more standardized products (low risk/low return), whereas wealthier ones could choose to purchase more sophisticated financial products (high risk/high returns). Therefore, if there were an increase in the IC share, as might occur in our model, this would concern lower income individuals, thus involving a lower demand for sophisticated products, and, consequently, minor product differentiation.

7.2 Quasi-informed consumers and maximum product differentiation

We are now going to consider the following subcase $\left( \underline{\theta }\le \theta ^{*}\le \theta ^{\prime }\le \theta ^{\prime \prime }\le \bar{\theta }\right)$, where $\theta ^{\prime }$ is not influential, being located in the IC range: $\theta ^{*}\le \theta ^{\prime }\le \theta ^{\prime \prime },$where $\theta ^{\prime \prime }$ is relevant to determine market demand. It is, thus, more appropriate to rewrite the restriction as: $\left( \underline{\theta }\le \theta ^{\prime }=\theta ^{*}\le \theta ^{\prime \prime }\le \bar{\theta }\right) .$

As can be noticed in Fig. 4, the location of $\theta ^{\prime }$ mainly depends on the small difference between the utility function slope of UC choosing high-quality goods ($q_{E}$), and the one of the IC making the same choice ($q_{H}$ ). Such a difference transforms UC into quasi-informed consumers. Consequently, all UC included in the range $\underline{\theta } \le \theta ^{*}=\theta ^{\prime }$ purchase low-quality goods, as do IC located nearby, in the range: $\theta ^{*}=\theta ^{\prime }\le \theta ^{\prime \prime }$. High-quality goods are only bought by consumers with the highest wtp.

Fig. 4

Utility functions and demand segments

The previous parameter restriction implies the following price domains for demand functions:

$$\begin{aligned} P_{H}-\bar{\theta }\Delta\le & {} P_{L}\le P_{H}-\theta ^{*}\Delta _{E} \\ P_{L}+\theta ^{*}\Delta _{E}\le & {} P_{H}\le P_{L}+\bar{\theta }\Delta \end{aligned}$$

As for the demand segments, $D_{L}$ derives both from UC with the lowest wtp $(\theta ^{*}-\underline{\theta })$ and from the contiguous IC share: $(\theta ^{\prime \prime }-\theta ^{*})$. By summing up the two shares, we obtain $D_{L}=\left( \theta ^{\prime \prime }-\underline{\theta }\right)$ , while $D_{H}$ just depends on IC: $D_{H}=\left( \bar{\theta }-\theta ^{\prime \prime }\right) .$

Demand functions turn out to be identical to those of the standard vertical differentiation model with perfect information we started from (Tirole 1989). Actually firm L in this case sells to consumers with low wtp, and firm H to consumers with high wtp, as is expected in the standard model.

Proposition 9

When UC are quasi-informed, $q_{L}$ is bought by all UC, and by the contiguos IC share, while $q_{H}$ is only bought by IC. Hence the model collapses to standard vertical differentiation with perfect information, despite the persistence of information disparity. Therefore, equilibrium prices are driven by $\Delta$ , and vertical differentiation is only limited by the cost of the quality effort.

Proof

By backward induction, we obtain the following equilibrium prices in the second stage game:

$$\begin{aligned} P_{L}^{*}=\frac{\Delta \left( \bar{\theta }-2 \underline{\theta }\right) }{3}\qquad P_{H}^{*}=\frac{\Delta \left( 2\bar{\theta }- \underline{\theta }\right) }{3} \end{aligned}$$

(28)

Equilibrium prices are identical to those arising in the standard vertical differentiation model. By checking if equilibrium prices are included in the price domains shown above, we obtain: $\theta ^{*}\le \frac{\Delta \left( 2 \underline{\theta }+1\right) }{3\Delta _{E}}$. As in the previous case, this restriction is not sufficient to discriminate between the situations where either UC or IC prevail within the market, unless further parameter restrictions are introduced.

Regarding the proof of the quality choice, details are included in “Appendix 2”. As usual, firm L minimizes quality, and $q_{L}^{*}=q_{0}.$ Solving the quality maximization problem for firm H, we obtain an interior solution for $q_{H}$:

$$\begin{aligned} q_{H}^{*}=\frac{\left( \bar{\theta }-2 \underline{\theta } \right) ^{2}}{18\alpha } \end{aligned}$$

(29)

According to the latter, the increase in $q_{H}$ is restricted only by the growth of the quality effort cost through $\alpha$¹⁷.

In addition, checking for equilibrium qualities included in the price domains of the demand functions, we can derive a further restriction concerning $q_{H}^{*}$

$$\begin{aligned} q_{H}^{*}\ge q_{0}+\frac{3\Delta _{E}\theta ^{*}}{1+2 \underline{\theta }} \end{aligned}$$

(30)

because $\left( q_{H}^{*}-q_{0}\right) =\Delta ^{*}$; by rearranging the previous inequality, we get:

$$\begin{aligned} \frac{\Delta _{E}}{\Delta ^{*}}\le \frac{1+2 \underline{\theta }}{3\theta ^{*}} \end{aligned}$$

(31)

Accordingly UC need to be only slightly optimistic, i.e. $\Delta _{E}$ is closer to $\Delta ^{*},$as if UC were quasi-informed. Concerning the brand premium, it can be easily seen that it is identical in this case to the one we derived in the previous section.

What is also interesting to notice is that we have obtained equilibrium results like the ones in the standard model, despite the persistence of information disparity. However, the fact that all UC purchase from firm L, as the contiguous IC share do, makes information disparity irrelevant in this framework.

8 Conclusion

Our model sheds more light on what would be the effect of extending consumer information in markets with vertical differentiation, information disparity, and optimistic misperception. For example, such a setting might be considered by governments aiming to carry out public policies in the domain of quality information. Even though we neglected welfare analysis, we have shown that the effects of extending quality information to more and more consumers cannot be taken for granted.

Even when there is a majority of UC, we have proven that increasing the IC share enhances the level of the optimal quality chosen by a high-quality firm. Yet quality misperception also boosts product differentiation, contributing to induce firms to choose higher quality levels. Actually we have discovered that brand premia are also driven by real quality improvements, not only by misperception rents. However, equilibrium prices appear to be ’excessive’, even considering quality premia, as quality expectations are never fulfilled in equilibrium, though prices always reflect optimistic misperception.

This result appears to be similar to the signaling effect of prices in models with asymmetric information about product quality. There is, however, a striking difference between the two theoretical settings, as consumers in those models have rational expectations, and higher prices are consistent with sales of higher quality goods. On the contrary, higher equilibrium prices in our framework are coherent with UC optimistic expectations, but do not reflect real quality differentials, which are lower than anticipated.

Furthermore, while in seminal models introducing information disparity, a higher IC share has always been correlated with the sale of higher quality goods, in our model such a result is achieved only in the first equilibrium. Growth of the IC share in the second one only contributes to reduce the difference in equilibrium prices, and the related brand premium, given minimum product differentiation. Increasing the IC share in the third equilibrium leads to less product differentiation, because the high-quality firm is bound to decrease its optimal quality level to match price reductions necessary to extend its market share. On the other hand, it is the drop of the IC share that implies the choice of a higher quality level for firm H.

Finally, concerning consumers’ externalities, they can be observed in the first two equilibria, where price and quality competition concern both IC and UC. In the third equilibrium, being UC not involved in market competition, there is no interaction between UC and IC, and, consequently, consumers’ externalities are absent. Nevertheless, UC can benefit from price reduction resulting from competition for IC. However, our approach allows to point out that UC misperceive price reduction as a bargain, whereas they are experiencing a ’rip-off’, because they are overoptimistic and not informed of the fact that product quality has been reduced, as well.

Extensions of our model could evaluate the introduction of the entry stage, and the related cost of quality provision. The consideration of N firms could also be interesting, as in Belleflamme and Forlin’s (2020) recent analysis, where Cournot competition replaces price competition. This approach allows to evaluate the size of demand segments. The convenience of vertical differentiation is explored by examining the cost to quality ratio. Furthermore, vertical differentiation models with multi-characteristic product preferences could also be investigated, for example, by adding an extra product characteristic with perceived quality, and taking into account attribute dependence as in Novo-Peteiro (2020).

Appendices

Appendix 1: Complete specification of demand functions for the first two cases

1.1 Case 1 (Section 6.1): Demand functions

On the basis of the parameter restriction

$$\begin{aligned} \left( \underline{\theta }\le \theta ^{\prime }\le \theta ^{\prime \prime }\le \theta ^{*}\le \bar{\theta }\right) \end{aligned}$$

we can derive the following price domains of the defined demand segments

$$\begin{aligned} P_{H}-\theta ^{*}\Delta\le & {} P_{L}\le P_{H}- \underline{\theta }\Delta _{E} \\ P_{L}+ \underline{\theta }\Delta _{E}\le & {} P_{H}\le P_{L}+\theta ^{*}\Delta \end{aligned}$$

for $D_{L},$ and $D_{H}$ respectively. In order to complete the definition of the demand functions, we can still refer to the restriction above, at first, considering the case where $\underline{\theta }=\theta ^{\prime }$ implying $D_{L}=0$, as UC that used to buy $q_{L}$ have now switched to $q_{H}$, and therefore, firm H has captured the entire market: $D_{H}=\left( \bar{\theta }-\underline{\theta }\right) =1.$From $\underline{ \theta }=\theta ^{\prime }$we can also obtain the following price domains for $D_{H}=\left( \bar{\theta }-\underline{\theta }\right) =1$: 0 $\le P_{H}\le P_{L}+ {\theta }\Delta _{E}.$

Likewise, by assuming $\bar{\theta }=\theta ^{*}=\theta ^{\prime },$we get $D_{H}=0$ and $D_{L}=\left( \bar{\theta }-\underline{\theta }\right) =1,$ where the latter is defined within the following price domain: 0 $\le P_{L}\le P_{H}-\theta ^{*}\Delta$. Demand functions are, consequently, represented in Figs. 5 and 6.

Fig. 5

Demand function for the low quality good

Fig. 6

Demand function for the high quality good

1.2 Case 2 (Section 6.2): Demand Functions

According to the parameter restriction

$$\begin{aligned} \left( \underline{\theta }\le \theta ^{\prime }\le \theta ^{*}\le \bar{\theta }\right) \end{aligned}$$

we can also define the price domains which are given by

$$\begin{aligned} P_{H}-\theta ^{*}\Delta _{E}\le & {} P_{L}\le P_{H}- \underline{\theta }\Delta _{E}\text { }; \\ P_{L}+ \underline{\theta }\Delta _{E}\le & {} P_{H}\le P_{L}+\theta ^{*}\Delta _{E}\text { } \end{aligned}$$

for $D_{L},$ and for $D_{H}$ respectively. To complete the definition of the demand functions, complying with the previous parameter restriction, we must also consider two further cases: (1) The one resulting from $\theta ^{\prime }=\theta ^{*},$ when even consumers with intermediate willingness to pay are informed and buy $q_{L}$ , and we obtain $D_{L}=\left( \bar{\theta }- \underline{\theta }\right) =1$, on the basis of the following price domain: $0\le P_{L}\le P_{H}-\theta ^{*}\Delta _{E}$; (2) The opposite case results from $\theta ^{*}=\bar{\theta }$ and $\theta ^{\prime }= {\theta }$ , where only UC buy $q_{H}$ because of their optimistic misperception, so that $D_{H}=\left( \bar{\theta } - \underline{\theta }\right) =1$ is defined in the following price domain: $0\le P_{H}\le P_{L}+ \underline{\theta }\Delta _{E}$. Therefore, demand functions can be represented as in Figs. 7 and 8.

Fig. 7

Demand function for the low quality good

Fig. 8

Demand function for the high quality good

Appendix 2: Complete proofs of the propositions regarding quality choice

1.1 Complete Proof of Proposition 1

Through substitution of equilibrium prices into profit functions, we obtain:

$$\begin{aligned} \Pi _{L}^{*}=\frac{\Delta _{E}\left( \bar{\theta }-2 \underline{\theta }\right) ^{2}}{9}-\alpha q_{L}^{2}\qquad \Pi _{H}^{*}= \frac{\Delta _{E}\left( 2\bar{\theta }- \underline{\theta }\right) ^{2}}{9}-\alpha q_{H}^{2} \end{aligned}$$

We can now examine the first stage, where the real quality differential $\Delta ^{*}$ is derived from. Considering profit maximization for firm L with respect to $q_{L},$ we get: $\frac{\partial \Pi _{L}}{\partial q_{L} }=\frac{4\bar{\theta } \underline{\theta }-\bar{\theta }^{2}-4 {\theta }^{2}}{9}-2\alpha q_{L}\le 0$. Therefore, it is optimal to minimize $q_{L}$. Due to compliance with the MQS, $q_{L}^{*}=q_{0}$ $>Min(q_{L}).$

Profit maximization for firm H, with respect to $q_{H},$ determines:

$$\begin{aligned} \frac{\partial \Pi _{H}}{\partial q_{H}}=-2\alpha q_{H}<0. \end{aligned}$$

However, firm H in this case is prevented from choosing the MQS $q_{0}$, because its demand also depends on IC who can evaluate $q_{H}.$

Actually, the key to understand the optimal strategy for firm H is to notice that $q_{H}^{*}$ represents the minimum quality level above $q_{0}$ that firm H needs to guarantee to the IC share, i.e $(\bar{\theta }-\theta ^{*})$. Accordingly, $q_{H}^{*}$ can be derived from IC incentive to purchase a high-quality product rather than a low-quality one, given the equilibrium prices determined in the second stage game, i.e. : $\theta ^{*}q_{H}-P_{H}^{*}>\theta ^{*}q_{0}-P_{L}^{*}$.

Let us point out that $\theta ^{*}$ , in fact, represents the marginal informed consumer, in our case $\theta ^{\prime \prime }\le \theta ^{*}$ , $\theta ^{\prime \prime }$ having no effects when it is located in the range $\theta ^{\prime }<$ $\theta ^{\prime \prime }<\theta ^{*},$ as all consumers within it are UC. Therefore, $\theta ^{\prime \prime }$ is relevant from $\theta ^{*}$ onwards, when consumers are informed. Considering, in addition, that equilibrium prices obtained in the second stage are anticipated in the first one, $\theta ^{\prime \prime }=\frac{ P_{H}^{*}-P_{L}^{*}}{q_{H}^{*}-q_{0}}=\theta ^{*}$in equilibrium. Consequently, we can derive the optimal level of high quality $q_{H}^{*}$ from this last equality

$$\begin{aligned} q_{H}^{*}=q_{0}+\frac{\Delta _{E}\left( 2 \underline{\theta } +1\right) }{3\theta ^{*}} \end{aligned}$$

(32)

with $q_{H}^{*}>q_{0}$ and $\Delta ^{*}>0$.

Moreover, we can also prove that $\Delta ^{*}<\Delta _{E}$. Given the expression of $q_{H}^{*}$ , we have $\Delta ^{*}=\left( q_{H}^{*}-q_{0}\right) =\frac{\Delta _{E}\left( 2 \underline{\theta } +1\right) }{3\theta ^{*}}$. As a result, $\Delta ^{*}<\Delta _{E}$ if $\frac{\left( 2 \underline{\theta }+1\right) }{3\theta ^{*}} <1$ implying $3\theta ^{*}>\left( 2 \underline{\theta } +1\right)$ or $\theta ^{*}>\frac{\left( 2 \underline{\theta } +1\right) }{3}$. As equilibrium restrictions on $\theta ^{*}$ indicate the minimum value of $\theta ^{*}=\frac{\Delta _{E}}{\Delta }\frac{ \left( 2 \underline{\theta }+1\right) }{3}$ and $\frac{\Delta _{E} }{\Delta }>1$with optimistic consumers, then $\theta ^{*}>\frac{\left( 2 \underline{\theta }+1\right) }{3}$ holds, and so $\Delta ^{*}<\Delta _{E}$.

Examining the expression of $q_{H}^{*}$, we can point out that it increases with $\Delta _{E}$ and with a decrease of $\theta ^{*},$ i.e. growth of the IC share $\left( 1-\theta ^{*}\right)$. The optimal quality level $q_{H}^{*}$ rises with $\Delta _{E}$ , because any augmentation of $\Delta _{E}$ implies higher equilibrium prices in the second game stage. Therefore, it has to be matched by growth of $q_{H}^{*}$ in the first stage, in order for both the IC incentive to buy $q_{H}$: $\theta ^{*}q_{H}^{*}-P_{H}^{*}>\theta ^{*}q_{0}-P_{L}^{*}$ , and the IC participation constraint: $\theta ^{*}q_{H}^{*}-P_{H}^{*}>0$ be satisfied. As equilibrium prices go up, due to the raise of $\Delta _{E},$ they should always be matched by an increase of $q_{H}^{*}$. However, UC expectations are never fulfilled, because $\Delta _{E}>\Delta ^{*},$ as proven previously.

Furthermore, the fact that $q_{H}^{*}$ rises together with the IC share $(1-\theta ^{*})$ can be explained by considering that while $\theta ^{*}$ reduces, the equality $\theta ^{\prime \prime }=\theta ^{*}$ in equilibrium is reached at a lower and lower location of $\theta$ . The reduction of the $D_{H}$ segment due to UC is compensated by an increase of the $D_{H}$ segment depending on IC. The ensuing decrease of $\theta ^{\prime \prime }=\frac{P_{H}^{*}-P_{L}^{*}}{q_{H}^{*}-q_{0}}$ in equilibrium implies raising $q_{H}^{*}$ in the first stage game, when anticipating the growth of $P_{H}^{*}$ in the second. The increase in quality is costly but necessary to attract a larger IC share, including consumers with lower and lower wtp.¹⁸ Conversely, $q_{H}^{*}$ decreases as $\theta ^{*}$increases, i.e with the reduction of the IC share, so that the equality $\theta ^{\prime \prime }=\theta ^{*}$ occurs at a location of $\theta ^{\prime \prime }$ closer to $\bar{\theta }.$This indicates a drop of the $D_{H}$ segment due to IC, allowing firm H to attract them even with a lower level of $q_{H}^{*}$ given their greater wtp.

1.2 Complete Proof of Proposition 4

Given equilibrium prices, we obtain equilibrium profits as

$$\begin{aligned} \Pi _{L}^{*}=\frac{\Delta _{E}\left( 2-\theta ^{*}\right) ^{2}}{9} -\alpha q_{L}^{2}\qquad \Pi _{H}^{*}=\frac{\Delta _{E}\left( 1+\theta ^{*}\right) ^{2}}{9}-\alpha q_{H}^{2} \end{aligned}$$

Considering quality choice, starting from firm L, and deriving the f.o.c and s.o.c., we attain:

$$\begin{aligned} \frac{\partial \Pi _{L}}{\partial q_{L}}=-\frac{\theta ^{*^{2}}-4\theta ^{*}+4}{9}-2\alpha q_{L}\le 0\text { and }\frac{\partial ^{2}\Pi _{L}}{ \partial q_{L}^{2}}=-2\alpha q_{L} \end{aligned}$$

As usual $q_{L}^{*}=q_{0},$ due to compliance with the MQS. As far as firm H is concerned, through profit maximization with respect to $q_{H}$, we can reach:

$$\begin{aligned} \frac{\partial \Pi _{H}}{\partial q_{H}}=-2\alpha q_{H}\le 0;\frac{\partial ^{2}\Pi _{H}}{\partial q_{H}^{2}}=-2\alpha \le 0 \end{aligned}$$

The previous f.o.c. and s.o.c. account for the negative effect of the quality effort costs on the $q_{H}$ level, which, consequently, should be as low as possible. According to demand functions, all IC buy $q_{L}$, so when choosing $q_{H}$, firm H also needs to take the following IC incentive to purchase $q_{L}$: $\theta ^{*}q_{L}-P_{L}^{*}>\theta ^{*}q_{H}-P_{H}^{*},$ into account, which implies a further restriction on $q_{H}:$

$$\begin{aligned} q_{H}<q_{L}-\frac{\Delta _{E}\left( 1-2\theta ^{*}\right) }{3\theta ^{*}} \end{aligned}$$

We can notice that $\frac{\Delta _{E}\left( 1-2\theta ^{*}\right) }{ 3\theta ^{*}}<0$ , given the equilibrium restriction $\theta ^{*}> \frac{1}{2}$. Therefore, $q_{L}-\frac{\Delta _{E}\left( 1-2\theta ^{*}\right) }{3\theta ^{*}}>0$, implying that $q_{H}^{*}$ be positive. Both the f.o.c. and the previous restriction on $q_{H}$, determine that the optimal choice for firm H is to minimize the high- quality level. Yet, being the MQS binding for both firms, we have $q_{H}^{*}=q_{0}$ , as for firm L. We can also notice that $q_{H}^{*}=q_{0},$ is consistent with the previous constraint that we can write as $q_{h}<q_{0}-\frac{\Delta _{E}\left( 1-2\theta ^{*}\right) }{3\theta ^{*}},$with $-\frac{ \Delta _{E}\left( 1-2\theta ^{*}\right) }{3\theta ^{*}}>0.$

1.3 Complete Proof of proposition 6

Second stage equilibrium profits can be derived as:

$$\begin{aligned} \Pi _{L}^{*}=\frac{\Delta \left( 1-\theta ^{*}\right) ^{2}}{9} -\alpha q_{L}^{2}\qquad \Pi _{H}^{*}=\frac{\Delta \left( 2+\theta ^{*}\right) ^{2}}{9}-\alpha q_{H}^{2} \end{aligned}$$

Moving onto the quality selection stage, we obtain the usual minimization results for $q_{L}$ through profit maximization, and with the MQS $q_{L}^{*}=q_{0}$:

$$\begin{aligned} \frac{\partial \Pi _{L}}{\partial q_{L}}=-\frac{\theta ^{*^{2}}-2\theta ^{*}+1}{9}-2\alpha q_{L}\le 0;\frac{\partial ^{2}\Pi _{L}}{\partial q_{0}^{2}}=-2\alpha \end{aligned}$$

As to the maximization of $\Pi _{H}$with respect to $q_{H}$ , we can reach the f.o.c :

$$\begin{aligned} \frac{\partial \Pi _{H}}{\partial q_{H}}=\frac{\theta ^{*^{2}}+4\theta ^{*}+4}{9}-2\alpha q_{H}=0 \end{aligned}$$

and the optimal quality level for firm H as an interior solution:

$$\begin{aligned} q_{H}^{*}=\frac{\theta ^{*^{2}}+4\theta ^{*}+4}{18\alpha } \end{aligned}$$

Therefore, we can observe real product differentiation in equilibrium: $\Delta ^{*}=(\frac{\theta ^{*^{2}}+4\theta ^{*}+4}{18\alpha }-q{ _{0}).}$

What is interesting to point out is that product differentiation in equilibrium decreases with an increase of the IC share: $q_{H}^{*}$ reduces with $\theta ^{*}$- implying a rise of $\left( 1-\theta ^{*}\right)$ - and, in addition, with the cost parameter $\alpha$. As $D_{H}=1-\theta ^{\prime \prime }+\theta ^{*}$, we can notice that $D_{H}$ also declines with an expansion of the IC share, while the opposite is true for $D_{L}=(\theta ^{\prime \prime }-\theta ^{*}).$ Actually, as $\theta ^{*}$ is located between ${\theta }$ and $\theta ^{\prime \prime }$, any rise in the IC share leads to an extension of $D_{L}$ at the disadvantage of that share of $D_{H}$ related to UC with overoptimistic misperception and low wtp, i.e.$\left( \theta ^{*}- \underline{\theta }\right) .$

However, an increasing IC share implies a further effect on equilibrium market demand, when considering the share of $D_{H}$ due to IC, i.e. $\left( \bar{\theta }-\theta ^{\prime \prime }\right)$ , and the fact that firm H in the quality choice stage anticipates equilibrium prices in the second stage game. Finally, by substituting equilibrium prices into the $\theta ^{\prime \prime }$ expression, we obtain $\theta ^{\prime \prime }=\frac{1+2\theta ^{*}}{3}$, and $\left( \bar{\theta }-\theta ^{\prime \prime }\right) =$ $\left( 1-\frac{1+2\theta ^{*}}{3}\right)$. Therefore, a decrease of $\theta ^{*}$- i.e an increase of IC - heads to a ’lower’ location of $\theta ^{\prime \prime }$(i.e. $\theta ^{\prime \prime }$ moves towards $\underline{\theta }$), involving growth of $\left( \bar{\theta } -\theta ^{\prime \prime }\right)$, the segment of $D_{H}$ due to IC. We can point out that any reduction of $\theta ^{\prime \prime }$ induces firm H to compete with firm L to attract IC with lower and lower wtp¹⁹. Such a strategy implies a decrease of $P_{H}^{*}$ in the second stage game and is anticipated by the reduction of $q_{H}^{*}$ in the first one. Due to the fact that in equilibrium $\theta ^{\prime \prime }=\frac{ P_{H}^{*}-P_{L}^{*}}{q_{H}^{*}-q_{0}}$, any IC increase suggests that the location of $\theta ^{\prime \prime }$ become closer to $\theta ^{*}$, determining a reduction of both $P_{H}^{*}$ and $q_{H}^{*}$ together with the rise of $P_{L}^{*}$ in the second stage game.

In the opposite case, firm H benefits from the expansion of its market share due to overoptimistic consumers with a reduction in the IC share (at the disadvantage of firm L). Yet, given the growth in $\theta ^{\prime \prime }=\frac{1+2\theta ^{*}}{3}$ due to the rise of $\theta ^{*}$ (moving towards $\bar{\theta }$), the other segment of $D_{H}=$ $\left( \bar{ \theta }-\theta ^{\prime \prime }\right)$ will decline. Consequently, firm H is bound to attract consumers with higher and higher wtp²⁰. This strategy drives an increase of $P_{H}^{*}$ and $q_{H}^{*},$ together with lessening of $P_{L}^{*}$. As a result, fewer IC involve more product differentiation.

1.4 Complete Proof of Proposition 9

Let us examine equilibrium profits in the second stage game:

$$\begin{aligned} \Pi _{L}^{*}=\frac{\Delta \left( \bar{\theta }-2 \underline{\theta }\right) ^{2}}{9}-\alpha q_{L}^{2}\qquad \Pi _{H}^{*}=\frac{ \Delta \left( 2\bar{\theta }- \underline{\theta }\right) ^{2}}{9} -\alpha q_{H}^{2} \end{aligned}$$

By profit maximization in $q_{L}$ and $q_{H}$:

$$\begin{aligned} \frac{\partial \Pi _{L}}{\partial q_{L}}=\frac{4\bar{\theta } {\theta }-\bar{\theta }^{2}-4 { \theta }^{2}}{9}-2\alpha q_{L}\le 0 \end{aligned}$$

Despite the quality minimization of firm L, we can set $q_{L}=q_{0}$ , as in the previous cases. Concerning $q_{H}$ , we will obtain the following f.o.c.

$$\begin{aligned} \frac{\partial \Pi _{H}}{\partial q_{H}}=\frac{\bar{\theta }^{2}+4 {\theta }^{2}-4\bar{\theta } { \theta }}{9}-2\alpha q_{H}=0 \end{aligned}$$

implying an interior solution for $q_{H}:$

$$\begin{aligned} q_{H}^{*}=\frac{\left( \bar{\theta }-2 {\theta } \right) ^{2}}{18\alpha } \end{aligned}$$