Appendix (A)
The production function is given by
$${\text{X}} = {\text{F}}\left( {{\text{eL}},{\text{ K}}} \right);$$
where
$$ {\text{e}} = {\text{e}}\left( {{\text{w}},{\text{u}},{\text{E}}} \right) $$
is the labour efficiency function.
Profit maximizing conditions of a competitive firm are given by
$$ {\text{F}}_{1} = \frac{{\text{w}}}{{\text{e}}} $$
and \({\text{F}}_{2} = {\text{r}}\).
Since the production function satisfies constant returns to scale, from Eulers theorem, we have
$${\text{X}} = {\text{F}}_{1} {\text{ eL}} + {\text{F}}_{2} {\text{K}}.$$
So, using profit maximizing conditions, we have
$$ {\text{X}} = \frac{{\text{w}}}{{\text{e}}}{\text{ eL}} + {\text{rK}} $$
$$ \Rightarrow \frac{{\text{w}}}{{\text{e}}}{\text{ a}}_{{\text{L}}} + {\text{ra}}_{{\text{K}}} = 1 $$
where \({\text{a}}_{{\text{L}}} = \frac{{{\text{eL}}}}{{\text{X}}}\) and \({\text{a}}_{{\text{K}}} = \frac{{\text{K}}}{{\text{X}}}\) are the two input of output coefficients. Since the production function satisfies CRS, \({\text{a}}_{{\text{L}}}\) and \({\text{a}}_{{\text{K}}}\) are functions of capital-labour ratio, \(\frac{{\text{K}}}{{{\text{eL}}}}\). Again profit maximizing conditions ensure that \(\frac{{\text{K}}}{{{\text{eL}}}}\) is a function of factor price ratio, \(\frac{{{\raise0.7ex\hbox{${\text{w}}$} \!\mathord{\left/ {\vphantom {{\text{w}} {\text{e}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{e}}$}}}}{{\text{r}}}\). Hence \({\text{a}}_{{\text{L}}}\) and \({\text{a}}_{{\text{K}}}\) are also functions of \(\frac{{{\raise0.7ex\hbox{${\text{w}}$} \!\mathord{\left/ {\vphantom {{\text{w}} {\text{e}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{e}}$}}}}{{\text{r}}}\).
Appendix (B)
From Eqs. (1) and (2), we have
$$ {\uptheta }_{{\text{L}}} {\hat{\text{w}}} - {\uptheta }_{{\text{L}}} {\hat{\text{e}}} + {\uptheta }_{{\text{K}}} {\hat{\text{r}}} = 0; $$
(28)
and
$$ {\hat{\text{w}}} - {\hat{\text{e}}} + {\upvarepsilon }_{{\text{u}}} {\hat{\text{u}}} = - {\upvarepsilon }_{{\text{E}}} {\hat{\text{E}}}{.} $$
(29)
From Eq. (3), we obtain
$$ \frac{{\partial^{2} {\text{e}}}}{{\partial {\text{w}}^{2} }}\frac{{{\text{dw}}}}{{\text{w}}}\frac{{\left( {\text{w}} \right)^{2} }}{{\text{e}}} + \frac{{\partial {\text{e}}}}{{\partial {\text{w}}}}\frac{{{\text{dw}}}}{{\text{w}}}\frac{{\text{w}}}{{\text{e}}} - \frac{{\partial {\text{e}}}}{{\partial {\text{w}}}}\frac{{\text{w}}}{{{\text{e}}^{2} }}\left[ {\frac{{\partial {\text{e}}}}{{\partial {\text{w}}}}\frac{{{\text{dw}}}}{{\text{w}}}{\text{w}} + \frac{{\partial {\text{e}}}}{{\partial {\text{u}}}}\frac{{{\text{du}}}}{{\text{u}}}{\text{u}} + \frac{{\partial {\text{e}}}}{{\partial {\text{E}}}}\frac{{{\text{dE}}}}{{\text{E}}}{\text{E}}} \right] = 0. $$
(30)
Using Eqs. (3) and (30), we have
$$ {\text{e}}_{11} \frac{{\left( {\text{w}} \right)^{2} }}{{\text{e}}}{\hat{\text{w}}} - {\upvarepsilon }_{{\text{u}}} {\hat{\text{u}}} = {\upvarepsilon }_{{\text{E}}} {\hat{\text{E}}}{.} $$
(31)
where \({\upvarepsilon }_{{\text{u}}} = \frac{{\partial {\text{e}}}}{{\partial {\text{u}}}}\frac{{\text{u}}}{{\text{e}}} > 0\), \({\upvarepsilon }_{{\text{E}}} = \frac{{\partial {\text{e}}}}{{\partial {\text{E}}}}\frac{{\text{E}}}{{\text{e}}} > 0\) and \({\text{e}}_{11} = \frac{{\partial^{2} {\text{e}}}}{{\partial {\text{w}}^{2} }} < 0\).
From Eq. (4), we have
$$ {\uptheta }_{{\text{L}}} {{\sigma \hat{\text{W}}}} - {\uptheta }_{{\text{L}}} {{\sigma \hat{\text{e}}}} - {\uptheta }_{{\text{L}}} {{\sigma \hat{\text{r}}}} + {\hat{\text{X}}} = {\hat{\text{K}}}{.} $$
(32)
From Eq. (5), we obtain
$$ - {\uptheta }_{{\text{K}}} {{\sigma \hat{\text{W}}}} - \left( { - {\uptheta }_{{\text{K}}} {\upsigma } + 1} \right){\hat{\text{e}}} + {\uptheta }_{{\text{K}}} {{\sigma \hat{\text{r}}}} + \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{u}}} + {\hat{\text{X}}} = 0. $$
(33)
Using Eqs. (28), (29) and equations (31) to (33), we have
$$ {\hat{\text{w}}} = \frac{1}{\Delta }\left\{ { - {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}} + {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} {\hat{\text{K}}}} \right\}. $$
(34)
$$ {\hat{\text{e}}} = \frac{{\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)}}{\Delta }\left\{ { - {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}} + {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} {\hat{\text{K}}}} \right\}. $$
(35)
$$ {\hat{\text{r}}} = \frac{1}{\Delta }\left[ { - {\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}} - {\upvarepsilon }_{{\text{u}}} {\hat{\text{K}}}} \right)} \right]. $$
(36)
$$ {\hat{\text{u}}} = \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}{\hat{\text{E}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} {{\hat{\text{K}}}}\right.} \right]; $$
(37)
and
$$ {\hat{\text{X}}} = \frac{1}{\Delta }\left[ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}} + \left\{ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} {\upsigma } + \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right) + {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} {{\hat{\text{K}}}} \right)} \right\}} \right]; $$
(38)
where,
$$ \Delta = - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left\{ {\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{{\text{u}}}{{{\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)}}} \right\}. $$
Equations (34) to (38) are same as Eqs. (6) to (10) in the body of the paper.
Appendix (C)
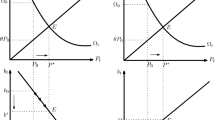
3.1 C.1 Slopes of stationary loci
We derive the slopes of two stationary loci \(\dot{\mathrm{K}}=0\) and \(\dot{\mathrm{E}}=0\) in this section.
Equations (12) and (13) presented below describe the rate of change in capital stock and the rate of change in environmental quality respectively.
$$ {\dot{\text{K}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}} - {{\updelta K;}} $$
(12)
and
$$ {\dot{\text{E}}} = {{\uptau \text{rK}}} - {\upalpha \text{X}} + {\uppi \text{E}}{.} $$
(13)
We have \({\dot{\text{K}}} = {\dot{\text{E}}} = 0\); and hence, from Eqs. (12) and (13), we find that
$$ {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}} = {{\updelta K;}} $$
(14)
and
$$ {{\uptau \text{rK}}} = {\upalpha \text{X}} - {\uppi \text{E}}{.} $$
(15)
From Eq. (14), we have
$$ \begin{aligned} & \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{r}} + {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}} - {\updelta }} \right\}{\text{dK}} \hfill \\ & = - \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{E}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{E}}}}} \right\}{\text{dE}} \hfill \\ \end{aligned} $$
(39)
Using Eqs. (14) and (39), we have
$$ \begin{aligned} &\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right) - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}}} \right\}{\text{dK}}\;\;\;\left( {\text{using steady state condition}} \right) \hfill \\ & = - \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{E}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{E}}}}} \right\}{\text{dE}} \hfill \\ & \mathop \Rightarrow \limits^{ } \left[ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - {\text{s}}_{{\text{w}}} \left\{ {\frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right) + \frac{{{\text{wL}}}}{{\text{K}}}{\text{u}}\frac{{{\hat{\text{u}}}}}{{{\hat{\text{K}}}}} - \left( {1 - {\text{u}}} \right)\frac{{{\text{wL}}}}{{\text{K}}}\frac{{{\hat{\text{w}}}}}{{{\hat{\text{K}}}}}} \right\}} \right]{\text{dK}} \hfill \\ & = - \left[ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} + {\text{s}}_{{\text{w}}} \left\{ {\frac{{{\text{wL}}}}{{\text{E}}}\left( {1 - {\text{u}}} \right)\frac{{{\hat{\text{w}}}}}{{{\hat{\text{E}}}}} - \frac{{{\text{wL}}}}{{\text{E}}}{\text{u}}\frac{{{\hat{\text{u}}}}}{{{\hat{\text{E}}}}}} \right\}} \right]. \hfill \\ \end{aligned} $$
(40)
Using Eqs. (6), (8), (9) and (40), we obtain
$$ \begin{aligned}& \Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left\{ {\left( {1 - {\rm{u}}} \right) + {\rm{u}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left( {1 - {\rm{u}}} \right)\frac{{{{ {\uptheta }}_{\rm{K}}}{{ {\upvarepsilon }}_{\rm{u}}}}}{\Delta }} \right\}} \right]{\rm{dK}} \\&
= - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right. \\& \left. { +\, {{\rm{s}}_{\rm{w}}}\left[ { - \frac{{{\rm{wL}}}}{{\rm{E}}}\left( {1 - {\rm{u}}} \right)\frac{{{{{\uptheta }}_{\rm{K}}}{{ {\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}}}{\Delta }} \right.\left. { + \frac{{{\rm{wL}}}}{{\rm{E}}}{\rm{u}}\frac{1}{\Delta }{{ {\upvarepsilon }}_{\rm{E}}}\left\{ { - { {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. { + {{ {\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right.} \right]} \right]{\rm{dE}} \\&
\Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ {{{ {\upvarepsilon }}_{\rm{u}}}{{ {\uptheta }}_{\rm{K}}}\left( {1 - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{ {\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right)} \right.} \right. \\&
\left. {\left. {\left. { - {{ {\upvarepsilon }}_{\rm{u}}}{ {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{ {\upvarepsilon }}_{\rm{u}}}{{ {\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{ {\upvarepsilon }}_{\rm{u}}}{ {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - {{ {\upvarepsilon }}_{\rm{u}}}{{ {\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}} \right\}} \right]{\rm{dK}} \\&
= - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right. \\&
+ {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }\left[ { - {{ {\uptheta }}_{\rm{K}}}{{ {\upvarepsilon }}_{\rm{E}}}{\rm{u}}} \right.\left. { + {\rm{u}}{{ {\upvarepsilon }}_{\rm{E}}}\left\{ { - { {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. { + {{ {\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right.} \right]{\rm{dE}}\\&
\Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ { - {{ {\upvarepsilon }}_{\rm{u}}}{ {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{ {\upvarepsilon }}_{\rm{u}}}{{ {\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\\&
\left. {\left. {\left. {\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{ {\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\} + {{ {\upvarepsilon }}_{\rm{u}}}{ {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - {{{\upvarepsilon }}_{\rm{u}}}{{{\theta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}} \right\}} \right]{\rm{dK}}\\&
= - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\theta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\\&
+ {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }\left[ { - {{{\theta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}} \right.\left. { + {\rm{u}}{{{\upvarepsilon }}_{\rm{E}}}\left\{ { - {{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. { + {{{\theta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right.} \right]{\rm{dE}}\\&
\Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\theta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ {\Delta \left. {\left. {\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\theta }}_{\rm{K}}}} \right)} \right\}} \right\}} \right]{\rm{dK}}} \right.} \right.\\&
(from \,\,\, definition \,\,\, of \,\,\, \Delta \,\,\, from \,\,\, static \,\,\, model)\\&
= - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\left. { + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dE}}\\&
\Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - 1 + \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right]{\rm{dK}}} \right.\\&
= - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\left. { + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dE}} \\&
\Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dK}}\\&
= - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\left. { + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dE}} \\&
\Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dK}}\\&
= \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\left. { - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dE}}\\&
{\left. { \Rightarrow \frac{{{\rm{dE}}}}{{{\rm{dK}}}}} \right|_{{ {\dot \rm {K}}} = 0}} = \frac{{\rm{E}}}{{\rm{K}}}\frac{{{{{\upvarepsilon }}_{\rm{u}}}}}{{{{{\upvarepsilon }}_{\rm{E}}}}}\frac{{\left( {1 - {\rm{u}}} \right)}}{{\rm{u}}}\frac{{\left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right){\rm{r}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}\frac{1}{{\rm{E}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{1}{{\left( {1 - {\rm{u}}} \right)}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{{\rm{KE}}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]}}{{\left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right){\rm{r}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}\frac{1}{{\rm{E}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{1}{{\left( {1 - {\rm{u}}} \right)}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{{\rm{KE}}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]}}\\&
\Rightarrow {\left. {\frac{{{\bf{dE}}}}{{{\bf{dK}}}}} \right|_{{\bf{\dot K}} = 0}} = \frac{{\bf{E}}}{{\bf{K}}}\frac{{{{\bf{\varepsilon }}_{\bf{u}}}}}{{{{\bf{\varepsilon }}_{\bf{E}}}}}\frac{{\left( {1 - {\bf{u}}} \right)}}{{\bf{u}}}.\end{aligned}$$
So the slope of \(\dot{\mathrm{K}}=0\) stationary locus is positive and is independent of the value of \(\upsigma \).
From Eq. (15), we have
$$ \begin{aligned} &\left( {{\uptau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{E}}}} + {\uppi }} \right){\text{dE}} = - \left( {{\uptau \text{r}} + {\uptau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{K}}}}} \right){\text{dK}} \hfill \\ & \mathop \Rightarrow \limits^{ } \left( {\frac{{{\uptau \text{X}}}}{{\text{r}}}\frac{{\text{r}}}{{\text{E}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - {\upalpha }\frac{{\text{X}}}{{\text{E}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}} + {\uppi }} \right){\text{dE}} = - \left( {{\uptau \text{r}} + \frac{{{\uptau \text{K}}}}{{\text{r}}}\frac{{\text{r}}}{{\text{K}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\upalpha \text{X}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right){\text{dK}} \hfill \\ & \mathop \Rightarrow \limits^{ } \left\{ {\left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\left( {\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right)} \right\}{\text{dE}} = - \left\{ {\left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\left( {1 + \frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right) - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}{\text{dK}}{.} \hfill \\ \end{aligned} $$
(41)
Using Eqs. (15) and (41), we have
$$ \mathop \Rightarrow \limits^{ } \left\{ {\left( {\frac{{{\alpha X}}}{{\text{E}}} - {\uppi }} \right)\left( {\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right)} \right\}{\text{dE}} = \left\{ { - \left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\left( {1 + \frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right) + \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}{\text{dK}}{.} $$
(42)
Using Eqs. (8), (10) and (42), we obtain
$$\begin{aligned} &\Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\left( { - \frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} + \frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}{{{\uptheta }}_{\rm{L}}}{{\upsigma }}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\&
= \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left\{ {1 + \frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - \frac{1}{\Delta }\left\{ { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} + \frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)} \right. + {{{\uptheta }}_{\rm{K}}}\left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right\}} \right.\\& \quad
\left. { + \frac{{{\uppi \text{E}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\&
\Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\&
= \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\}\\&
\quad - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{k}}}{{\upsigma }}\left. {\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\&
\Rightarrow \left\{ {\left( {\frac{{{{\upalpha X}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\&
= \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\} - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\\&
\quad - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{k}}}{{\upsigma }}\left. {\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\&
\Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\&
= \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ \Delta \right.} \right. + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\left. {\left( {1 - {{{\uptheta }}_{\rm{K}}}} \right)\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\&
(from \,\,\, definition \,\,\, of \,\,\, \Delta \,\,\, from \,\,\, static \,\,\, model)\\&
\Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\&
= \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ \Delta \right.} \right. + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\left. {{{{\uptheta }}_{\rm{L}}}\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\&
\Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\&
= \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ \Delta \right.} \right. + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\left. {\left. {{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right)} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\&
\Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\&
= \left\{ {\left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right) + \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right\}{\rm{dK}}\\&
{\left. {\frac{{{\rm{dE}}}}{{{\rm{dK}}}}} \right|_{{\dot{\rm E}} = 0}} = \frac{{\left\{ {\left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right) + \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right\}}}{{\left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}}} \end{aligned} .$$
(43)
Now,
$$ \begin{aligned} &1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}} \hfill \\ & = 1 + \frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \hfill \\& = \frac{{\Delta + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}}}{\Delta } \hfill \\& = \frac{{ - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left\{ {\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{{\text{u}}}{{{\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)}}} \right\} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}}}{\Delta }~~(from \quad definition \quad of \quad from \quad static \quad model) \hfill \\& = \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left\{ {\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{{\text{u}}}{{{\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)}}} \right\}} \right. \hfill \\& \quad \left. { + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right] \hfill \\ &= \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} } \right. \hfill \\ & \quad \left. {+ {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right] \hfill \\ &= \frac{1}{\Delta }\left[ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} {\upsigma } + \frac{{{\uptheta }_{{\text{K}}} {\text{u}}}}{{\left( {1 - {\text{u}}} \right)}}} \right) + {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) + {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( { - {\upvarepsilon }_{{\text{u}}} + {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)} \right] \hfill \\ &= \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{1}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right) \hfill \\ \end{aligned} $$
Now from Eq. (19), we have
\(\left. {\frac{{{\text{dE}}}}{{{\text{dK}}}}} \right|_{{{\dot{\text{E}}} = 0}} = \frac{{\left\{ {\left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{L}}} \left( {{\upsigma } - 1} \right) + \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}}}{{\left\{ {\left( {\frac{{{\alpha X}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)} \right\}}}\).
If \({\upsigma } = 1\), then
\(\left. {\frac{{{\mathbf{dE}}}}{{{\mathbf{dK}}}}} \right|_{{{\dot{\mathbf{E}}} = 0}} = \frac{{\frac{{\mathbf{E}}}{{\mathbf{K}}}\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}}}}{{\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} + \frac{1}{\Delta }{\mathbf{\sigma e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\uptheta}}}_{{\mathbf{L}}} \left( {{{\varvec{\upvarepsilon}}}_{{\mathbf{E}}} \frac{{\mathbf{u}}}{{\left( {1 - {\mathbf{u}}} \right)}} - {{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} } \right)}}\)
.
Here the numerator is always positive and the denominator may be negative only if
\({\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)\).
Only in this case, second term of the denominator is negative. If \(\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\) is very low, this denominator may be negative and hence \({\dot{\text{E}}} = 0\) locus may slope negatively.
C.2 Stability analysis of the long-run equilibrium
Jacobian matrix corresponding to the differential Eqs. (14) and (15) is given by.
\({\text{J}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}} \\ \end{array} } \right]\).
Using Eq. (12), we have
$$ \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{r}} + {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}} - {\updelta }{.} $$
(44)
Using Eqs. (14) and (39), we have
$$ \begin{gathered} \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right) - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}} \hfill \\ \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - {\text{s}}_{{\text{w}}} \left[ {\frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right) + \frac{{{\text{wL}}}}{{\text{K}}}{\text{u}}\frac{{{\hat{\text{u}}}}}{{{\hat{\text{K}}}}} - \left( {1 - {\text{u}}} \right)\frac{{{\text{wL}}}}{{\text{K}}}\frac{{{\hat{\text{w}}}}}{{{\hat{\text{K}}}}}} \right]. \hfill \\ \end{gathered} $$
(45)
Using Eqs. (6), (8), (9) and (45), we obtain
$$\begin{aligned} &\frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left[ {\left( {1 - {\rm{u}}} \right) + {\rm{u}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left( {1 - {\rm{u}}} \right)\frac{{{{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{u}}}}}{\Delta }} \right]\\&
\Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left[ {\left( {1 - {\rm{u}}} \right) + {\rm{u}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left( {1 - {\rm{u}}} \right)\frac{{{{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{u}}}}}{\Delta }} \right]\\&
\Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left( {1 - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right)} \right.} \right.\\&
\left. {\left. { - {{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - {{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}} \right\}\\&
\Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ { - {{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\\&
\left. {\left. {\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\} + {{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - {{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}} \right\}\\&
\Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ {\Delta \left. {\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right\}} \right.} \right.\\ &
(from \quad definition \quad of \quad \Delta \quad from \quad static \quad model)\\&
\Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - 1 + \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\&
\Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right).\end{aligned}$$
(46)
If \({\upsigma } = 1\), then
$$ \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} $$
$$ \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = \frac{1}{\Delta }{\uptheta }_{{\text{L}}} \frac{1}{{\text{K}}}{\delta e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}}} \right\} $$
$$\Rightarrow \frac{{\partial {\dot{\mathbf{K}}}}}{{\partial {\mathbf{K}}}} = \frac{1}{\Delta }{{\varvec{\uptheta}}}_{{\mathbf{L}}} {\boldsymbol{\delta} \mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} < 0. ~~(\text{Using} ~~\text{Eq}. ~(14))$$
Using Eq. (12), we have
$$ \begin{gathered} \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{E}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{E}}}} \hfill \\ \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} + {\text{s}}_{{\text{w}}} \left[ {\frac{{{\text{wL}}}}{{\text{E}}}\left( {1 - {\text{u}}} \right)\frac{{{\hat{\text{w}}}}}{{{\hat{\text{E}}}}} - \frac{{{\text{wL}}}}{{\text{E}}}{\text{u}}\frac{{{\hat{\text{u}}}}}{{{\hat{\text{E}}}}}} \right]. \hfill \\ \end{gathered} $$
(47)
Using Eqs. (6), (8), (9) and (43), we obtain
$$ \begin{aligned} & \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = - {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \hfill \\ &\quad+ {\text{s}}_{{\text{w}}} \left[ { - \frac{{{\text{wL}}}}{{\text{E}}}\left( {1 - {\text{u}}} \right)\frac{{{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}}}{\Delta }} \right.\left. { + \frac{{{\text{wL}}}}{{\text{E}}}{\text{u}}\frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}} \right.} \right] \hfill \\ &
\mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = - {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \hfill \\ &
\quad + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{E}}}\frac{1}{\Delta }\left[ { - {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} {\text{u}}} \right.\left. { + {{\text{u}\upvarepsilon }}_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}} \right.} \right] \hfill \\ &
\mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = - {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{E}}}\frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} {\text{ue}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right). \hfill \\ \end{aligned} $$
(48)
If \({\upsigma } = 1\), then
$$\begin{aligned} &\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \\ & \Rightarrow \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = \frac{1}{\Delta }{\uptheta }_{{\text{L}}} \frac{1}{{\text{K}}}{\delta e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}}} \right\} \\ &\Rightarrow \frac{{\partial {\dot{\mathbf{K}}}}}{{\partial {\mathbf{K}}}} = \frac{1}{\Delta }{{\varvec{\uptheta}}}_{{\mathbf{L}}} {\boldsymbol{\delta} e}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} > 0. \, (\text{Using}~~ \text{Eq}.~~ (14)) \end{aligned}$$
Using Eq. (13), we have
$$ \begin{aligned} &\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}} = {\uptau \text{r}} + {\uptau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{K}}}} \hfill \\ &\Rightarrow \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}} = {\uptau \text{r}} + \frac{{{\uptau \text{K}}}}{{\text{r}}}\frac{{\text{r}}}{{\text{K}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\upalpha \text{X}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}. \hfill \\ \end{aligned} $$
(49)
From Eq. (15) and (49), we obtain
$$ \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}} = \left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\left( {1 + \frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right) - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}. $$
(50)
From Eq. (8), (10) and (50), we have
$$\begin{aligned}&\frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left\{ {1 + \frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{u}}} - \frac{1}{\Delta }\left\{ { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\varepsilon }}_{\rm{u}}}{{\upsigma }} + \frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)} \right. + {{{\uptheta }}_{\rm{K}}}\left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right\}\\&
\quad - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
\Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\}\\&\quad - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{k}}}{{\upsigma }}\left. {\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
\Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\} - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\\&
\quad - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{k}}}{ {\upsigma }}\left. {\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
\Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ \Delta + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} {\left( {1 - {{{\uptheta }}_{\rm{K}}}} \right)\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right]} \right. - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
\Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ \Delta + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} {{{{\uptheta }}_{\rm{L}}}\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right]} \right. - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
\Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ \Delta {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} {{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right)} \right]} \right] - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
\Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right) - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}.\end{aligned}$$
If \({\upsigma } = 1,\) then.
$$\frac{{\partial {\dot{\mathbf{E}}}}}{{\partial {\mathbf{K}}}} = - \frac{{{\mathbf{\pi E}}}}{{\mathbf{K}}}\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} < 0.$$
Using Eq. (13), we have
$$ \begin{aligned} &\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = {\uptau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{E}}}} + {\uppi } \\ & \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \frac{{{\uptau X}}}{{\text{r}}}\frac{{\text{r}}}{{\text{E}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - {\upalpha }\frac{{\text{X}}}{{\text{E}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}} + {\uppi } \\ & \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\left( {\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right). \end{aligned}$$
(51)
From Eq. (15) and (51), we obtain
$$ \begin{aligned}& \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\left( {\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) \hfill \\ & \Rightarrow \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\left( { - \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} + \frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) \hfill \\ & \Rightarrow \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) \hfill \\ & \Rightarrow \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right). \hfill \\ \end{aligned} $$
If \({\upsigma } = 1\), then
\(\frac{{\partial {\dot{\mathbf{E}}}}}{{\partial {\mathbf{E}}}} = {{\varvec{\uppi}}}\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} + \frac{{{\varvec{\uppi}}}}{\Delta }{\mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\uptheta}}}_{{\mathbf{L}}} \left( {{{\varvec{\upvarepsilon}}}_{{\mathbf{E}}} \frac{{\mathbf{u}}}{{\left( {1 - {\mathbf{u}}} \right)}} - {{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} } \right).\)
Here, \(\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} > 0\). However, if \({\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)\) and if \(\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\) is very low, then \(\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}\) may be negative.
Jacobian Determinant, \({\text{J}}\), is given by
$$\begin{aligned}&{\rm{J}} = \left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\&
\left\{ {\left( {\frac{{{\alpha {\rm X}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} - {{{\upvarepsilon }}_{\rm{u}}}} \right)} \right\} + \\&
\left\{ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\&
\left\{ {\left( {\frac{{{\alpha{\rm X}} - {{\uppi E}}}}{{\rm{K}}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right) + \frac{{{{\uppi E}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right\}\\&
= \left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\&
\left\{ {{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} - {{{\upvarepsilon }}_{\rm{u}}}} \right)} \right\} + \\&
\left\{ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\frac{{{{\uppi E}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
= {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right.\\&
\left. { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\} + \\&
\frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} - {{{\upvarepsilon }}_{\rm{u}}}} \right)\\&
\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\&
= {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right) - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)} \right\}} \right.\\&
+ \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} - {{{\upvarepsilon }}_{\rm{u}}}} \right)\\&
\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\&
= {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\&
- \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\\&
\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\&
= {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\&
- \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\\&
\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\&
= {{\uppi }}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\&
\left\{ {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right\}\\&
= {{\uppi }}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right){\rm{r}}{{{\uptheta }}_{\rm{L}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\&
\left\{ {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right\}\end{aligned}$$
If \({\upsigma } = 1\), then
$$ \begin{aligned} &\Rightarrow {\text{J}} = {\uppi }\left( {{\upvarepsilon }_{{\text{u}}} - {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \frac{1}{{\text{K}}}\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rk}} + \left. {{\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}}} \right\}} \right. \\ & \left\{ {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - \frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}} } \right\} \end{aligned} $$
\(\mathop \Rightarrow \limits^{ } {\mathbf{J}} = \left( {{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} - {{\varvec{\upvarepsilon}}}_{{\mathbf{E}}} \frac{{\mathbf{u}}}{{\left( {1 - {\mathbf{u}}} \right)}}} \right)\frac{{{\varvec{\uppi}}}}{\Delta }{\mathbf{\delta \theta }}_{{\mathbf{L}}} {\mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}\left( {\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} - \frac{1}{\Delta }{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} {\mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\uptheta}}}_{{\mathbf{L}}} {{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} } \right) > 0\) (Using Eq. (14))
if \({\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)\).
Trace of Jacobian Matrix is \(= \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} + \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}\).
Here,
$$ \begin{aligned} &\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} + \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} \hfill \\ & = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right) \hfill \\ &\quad + \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right) \hfill \\ \end{aligned} $$
If \({\upsigma } = 1\), then
Trace of Jacobian Matrix
$$= \frac{1}{\Delta }{{\varvec{\uptheta}}}_{{\mathbf{L}}} {\mathbf{\delta e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} + {{\varvec{\uppi}}}\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} + \frac{{{\varvec{\uppi}}}}{\Delta }{\mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\uptheta}}}_{{\mathbf{L}}} \left( {{{\varvec{\upvarepsilon}}}_{{\mathbf{E}}} \frac{{\mathbf{u}}}{{\left( {1 - {\mathbf{u}}} \right)}} - {{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} } \right).$$
Here the first term is always negative and the third term is also negative if
\({\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)\).
However, the second term, \({\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} > 0\). If \(\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\) is very low, then trace may be negative and the steady state equilibrium may be stable.
Appendix (D)
From Eq. (14), we have
$$ \begin{aligned} &\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{r}} + {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}} - {\updelta }} \right\}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} \hfill \\&\quad + \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{E}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{E}}}}} \right\}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = {\text{rK}} \hfill \\ \end{aligned} $$
(52)
Using Eqs. (6), (8), (9) and (40), we obtain
$$ \begin{aligned}& \left[ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} {\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right)} \right]\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} \hfill \\ & - \left[ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right.\left. { - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{E}}}\frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} {\text{ue}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right)} \right]\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = {\text{rK}} \hfill \\ &\mathop \Rightarrow \limits^{ } \left[ {\frac{1}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} {\left( {{\upsigma } - 1} \right)} \right]\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} \hfill \\ &- \left[ {\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right.\left. {\frac{{{\delta K}}}{{\text{E}}} + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{E}}}\frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} {\text{ue}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upsigma } - 1} \right)} \right]\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = {\text{rK}}. \hfill \\ \end{aligned} $$
(53)
From Eq. (15), we have
$$ \left( {{\tau \text{r}} + {\tau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{K}}}}} \right)\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} + \left( {{\tau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{E}}}} + {\uppi }} \right)\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}{.} $$
(54)
Using Eqs. (8), (10) and (41), we obtain
$$ \begin{aligned} &- \left\{ {\left( {\frac{{{\alpha X} - {\uppi \text{E}}}}{{\text{K}}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{L}}} \left( {{\upsigma } - 1} \right) + \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} \hfill \\ &+ \left\{ {\left( {\frac{{{\alpha X}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)} \right\}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}{.} \hfill \\ \end{aligned} $$
(55)
Using Eqs. (53) and (56), we have
$$\frac{{{\rm{dK}}}}{{{\rm{d}\uptau }}} = {\rm{rK}}\frac{{\frac{{{{{\uptheta }}_{\rm{L}}}}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}{\rm{E}}\left( {{{\uppi \text{E}}} - {{\updelta \text{K}}}} \right) - {{\uppi }}{{{\upvarepsilon }}_{\rm{u}}}} \right\} + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\frac{1}{{\rm{E}}}\left( {{{\upsigma }} - 1} \right)\left\{ { - {{\rm{s}}_{\rm{w}}}{\rm{wL}}\left( {1 - {\rm{u}}} \right) + \left( {{{\upalpha \text{X}}} - {{\uppi \text{E}}}} \right){{{\uptheta }}_{\rm{L}}}} \right\}}}{{{{\uppi }}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right){\rm{r}}{{{\uptheta }}_{\rm{L}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\left\{ {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right\}}};$$
(56)
and
$$ \frac{{{\text{dE}}}}{{{\text{d}\uptau }}} = - {\text{rK}}\frac{{\frac{1}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \frac{1}{{\text{K}}}\left( {{\upsigma } - 1} \right)\left\{ {{\text{s}}_{{\text{w}}} {\text{wL}}\left( {1 - {\text{u}}} \right) - \left( {{\upalpha \text{X}} - {\uppi \text{E}}} \right){\uptheta }_{{\text{L}}} } \right\}}}{{{\uppi }\left( {{\upvarepsilon }_{{\text{u}}} - {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){{\text{r} \uptheta }}_{{\text{L}}} - \left. {{\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right)} \right\}\left\{ {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - \frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}} } \right\}} \right.}}. $$
(57)
Equations (56) and (57) are same as Eqs. (18) and (19) in the body of the paper.
If \({\upsigma } = 1\).
then from equations (56) and (57), we obtain
$$\frac{{{\rm{dK}}}}{{{\rm{d}\uptau }}} = {\rm{rK}}\frac{{\frac{{{{{\uptheta }}_{\rm{L}}}}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}{\rm{E}}\left( {{{\uppi E}} - {{\updelta K}}} \right) - {{\uppi }}{{{\upvarepsilon }}_{\rm{u}}}} \right\} + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}}}{{\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{{{\uppi }}}{\Delta }{{\updelta }}{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right)}};$$
(58)
and
$$ \frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}\frac{{\frac{1}{\Delta }{{\updelta \theta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} - \frac{{{\uppi E}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}}}{{\left( {{\upvarepsilon }_{{\text{u}}} - {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)\frac{{\uppi }}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - \frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}} } \right)}}. $$
(59)
Equations (58) and (59) are same as Eqs. (20) and (21) in the body of the paper.
From Eq. (9), we have
$$ \begin{aligned} & {\hat{\text{u}}} = \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\upsigma \text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}{\hat{\text{E}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. {{\hat{\text{K}}}} \right] \hfill \\ & \Rightarrow \frac{{{\text{du}}}}{{{\text{d}\uptau}}} = \frac{{\text{u}}}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\upsigma \text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\frac{1}{{\text{E}}}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. {\frac{1}{{\text{K}}}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}}} \right]. \hfill \\ \end{aligned} $$
(60)
Using equations (58)–(60), we obtain
$$\frac{{{\rm{du}}}}{{{\rm{d}\uptau }}} = \frac{{\rm{u}}}{\Delta }\left[ {{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}} {\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{\rm{r}}\frac{{\frac{{{{{\uptheta }}_{\rm{L}}}}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}{\rm{E}}\left( {{{\uppi \text{E}}} - {{\updelta \text{K}}}} \right) - {{\uppi }}{{{\upvarepsilon }}_{\rm{u}}}} \right\} + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}}}{{\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{{{\uppi }}}{\Delta }{{\updelta }}{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right)}}} \right] $$
Equation (60) is same as Eq. (23) in the body of the paper.
Appendix (E)
6.1 E.1 Ramsey Problem
6.1.1 Rate of Growth of Consumption
The representative consumer maximizes \(\mathop \int \limits_{0}^{ \propto } \left[ {\frac{{\left( {{\text{C}}^{{\upmu }} {\text{E}}^{{1 - {\upmu }}} } \right)^{1 - \vartheta } - 1}}{1 - \vartheta } - {\text{V}}\left( {\text{e}} \right)} \right]{\text{e}}^{{ - {\rho t}}} {\text{dt}}\) subject to the equation of motion given by
$$ {\dot{\text{K}}} = {\text{sY}} - {\delta K}{.} $$
(61)
\({\text{K}}\left( 0 \right)\) is given. \({\text{K}}\) is the state variable; and \({\text{s}}\) and \({\text{e}}\) are two control variables.
The Current value Hamiltonian to be maximized at each point of time is given by
$${\rm{H}} = \left[ {\frac{{{{\left( {{{{\bar{\rm C}}}^{{\upmu }}}{{\rm{E}}^{1-{{\upmu }}}}} \right)}^{1-\vartheta }}-1}}{{1-\vartheta }}-{\rm{V}}\left( {\rm{e}} \right)} \right]{{\rm{e}}^{-{{\uprho \text{t}}}}} + {\rm{q}}{{\rm{e}}^{-{{\uprho \text{t}}}}}{\dot{\rm K}};$$
(62)
where, \({\text{q}}\) is the co-state variable.
Using equations (61) and (62) and the expression of \({\overline{\text{Y}}}\), we have
$$ \begin{aligned} &{\text{H}} = \frac{{\left( {{\overline{\text{C}}}^{{\upmu }} {\text{E}}^{{1 - {\upmu }}} } \right)^{1 - \vartheta } - 1}}{1 - \vartheta }{\text{e}}^{{ - {\rho t}}} + {\text{qe}}^{{ - {\rho t}}} \left\{ {\left( {{\overline{\text{Y}}} - {\overline{\text{C}}}} \right) - {{\updelta K }}} \right\} - {\text{V}}\left( {\text{e}} \right){\text{e}}^{{ - {\rho t}}} , \hfill \\ & \Rightarrow {\text{H}} = \frac{{\left( {{\overline{\text{C}}}^{{\upmu }} {\text{E}}^{{1 - {\upmu }}} } \right)^{1 - \vartheta } - 1}}{1 - \vartheta }{\text{e}}^{{ - {\rho t}}} + {\text{qe}}^{{ - {\rho t}}} \left[ {{\text{p}}\left( {\text{e}} \right){\text{w}} + \left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)\left( {1 - {\text{u}}} \right){\text{w}}^{*} + \left( {1 - {\uptau }} \right){\text{rK}}} \right] \hfill \\ & - {\text{qe}}^{{ - {\rho t}}} {{\uptau rK}} - {\text{qe}}^{{ - {\rho t}}} {\overline{\text{C}}} - {{\updelta Kqe}}^{{ - {\rho t}}} . \hfill \\ \end{aligned} $$
(63)
The representative consumer is a taker of, \({\text{r}}\) and \({\text{w}}\) and \({\text{w}}^{*}\). \({\text{H}}\) is to be maximized with respect to \({\text{s}}\) and \({\text{e}}\). Since \({\overline{\text{C}}}\) is a function of \({\text{s}}\) and \({\text{e}}\), we obtain the same solution maximizing \({\text{H}}\) with respect to \({\overline{\text{C}}}\) and \({\text{e}}\). The first order interior optimality condition with respect to \({\overline{\text{C}}}\) is given by
$$ \begin{gathered} \left[ {{{\upmu \overline{\text{C}}}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} - {\text{q}}} \right]{\text{e}}^{{ - {\rho t}}} = 0, \hfill \\ \Rightarrow {{\upmu \overline{\text{C}}}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} = {\text{q}}. \hfill \\ \end{gathered} $$
(64)
Similarly the first order interior optimality condition with respect to \({\text{e}}\) is given by
$$ \left[ {\left( {1 - {\text{s}}} \right){{\upmu \overline{\text{C}}}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} + {\text{qs}}} \right]\frac{{\partial {\overline{\text{Y}}}}}{{\partial {\text{e}}}} = {\text{V}^{\prime}}\left( {\text{e}} \right), $$
(65)
where
$$ \frac{{\partial {\overline{\text{Y}}}}}{{\partial {\text{e}}}} = {\text{p}^{\prime}}\left( {\text{e}} \right)\left[ {{\text{w}} - {\text{w}}^{*} + {\text{w}}^{*} {\text{u}}} \right]. $$
From equation (65) and using \({\text{C}} = {\overline{\text{C}}}\) in the general equilibrium, we have
$$ \frac{{{\dot{\text{C}}}}}{{\text{C}}} = \frac{1}{{\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right)}}\frac{{{\dot{\text{q}}}}}{{\text{q}}} - \frac{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}}{{\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right)}}\frac{{{\dot{\text{E}}}}}{{\text{E}}}. $$
(66)
Optimum time path of the co-state variable satisfies the following differential equation.
$$ \begin{aligned} & {\dot{\text{q}}} = {\rho q} - \frac{{\partial {\text{He}}^{{{\rho t}}} }}{{\partial {\text{K}}}}, \hfill \\ & \mathop \Rightarrow \limits_{ } \frac{{{\dot{\text{q}}}}}{{\text{q}}} = {\uprho } + {\updelta } - {\text{r}}\left( {1 - {\uptau }} \right) \hfill \\ \end{aligned} $$
(67)
Using equations (66) and (67), we obtain
$$ \frac{{{\dot{\text{C}}}}}{{\text{C}}} = \frac{{{\text{r}}\left( {1 - {\uptau }} \right) - {\updelta } - {\uprho }}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}} - \frac{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}}{{\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right)}}\frac{{{\dot{\text{E}}}}}{{\text{E}}}. $$
(68)
Equation (68) is same as Eq. (24) in the body of the paper.
Using equations (64) and (65) and the expression of \(\frac{{\partial {\overline{\text{Y}}}}}{{\partial {\text{c}}}}\) and \({\text{C}} = {\overline{\text{C}}}\), we have
$$ {\upmu \text{C}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} {\text{p}^{\prime}}\left( {\text{e}} \right)\left[ {{\text{w}} - {\text{w}}^{*} + {\text{uw}}^{*} } \right] = {\text{V}^{\prime}}\left( {\text{e}} \right). $$
(69)
In the general equilibrium
$$ {\text{w}}^{*} \left( {1 - {\text{u}}} \right) = \frac{{{\text{w}}\left[ {1 - {\text{u}} - {\text{p}}\left( {\text{e}} \right)} \right]}}{{1 - {\text{p}}\left( {\text{e}} \right)}}. $$
So from equation (69), we have
$$ {\mu C}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} {\text{p}^{\prime}}\left( {\text{e}} \right)\left[ {\frac{{{\text{wu}}}}{{1 - {\text{p}}\left( {\text{e}} \right)}}} \right] = {\text{V}^{\prime}}\left( {\text{e}} \right). $$
(70)
Equation (70) is same as Eq. (26) in the body of the paper.
From equation (70), we have
$$ \left[ {\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right)} \right]\frac{{{\dot{\text{c}}}}}{{\text{c}}} + \left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)\frac{{{\dot{\text{E}}}}}{{\text{E}}} + \frac{{{\dot{\text{u}}}}}{{\text{u}}} + \frac{{{\dot{\text{w}}}}}{{\text{w}}} = \frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right)\frac{{{\dot{\text{e}}}}}{{\text{e}}} - \frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)}}\frac{{{\dot{\text{e}}}}}{{\text{e}}} - \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}\frac{{{\dot{\text{e}}}}}{{\text{e}}}. $$
(71)
Using equations (68) and (71), we have,
$$ \begin{aligned} & {\updelta } + {\uprho } - {\text{r}}\left( {1 - {\uptau }} \right) + \frac{{{\dot{\text{u}}}}}{{\text{u}}} + \frac{{{\dot{\text{w}}}}}{{\text{w}}} = \frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right)\frac{{{\dot{\text{e}}}}}{{\text{e}}} - \frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)}}\frac{{{\dot{\text{e}}}}}{{\text{e}}} - \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}\frac{{{\dot{\text{e}}}}}{{\text{e}}}, \hfill \\ &\Rightarrow \frac{{{\dot{\text{e}}}}}{{\text{e}}} = \frac{{{\updelta } + {\uprho } - {\text{r}}\left( {1 - {\uptau }} \right) + \frac{{{\dot{\text{u}}}}}{{\text{u}}} + \frac{{{\dot{\text{w}}}}}{{\text{w}}}}}{{\frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right) - \left( {\frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)}} + \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}} \right)}} \hfill \\ \end{aligned} $$
(72)
Using Eqs. (6) and (72), we have
$$ \frac{{{\dot{\text{e}}}}}{{\text{e}}} = \frac{{{\updelta } + {\uprho }-{\text{r}}\left( {1-{\uptau }} \right) + \frac{{{\dot{\text{u}}}}}{{\text{u}}} + \frac{1}{\Delta }\left\{ {-{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}\frac{{{\dot{\text{E}}}}}{{\text{E}}} + \left. {{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \frac{{{\dot{\text{K}}}}}{{\text{K}}}} \right\}} \right.}}{{\frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right)-\left( {\frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1-{\text{p}}\left( {\text{e}} \right)} \right)}} + \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}} \right)}}. $$
(73)
Using Eq. (9), we get
$$ \frac{{{\dot{\text{u}}}}}{{\text{u}}} = \frac{1}{\Delta }\left[ {-{\upvarepsilon }_{{\text{E}}} \left\{ {-{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\frac{{{\dot{\text{E}}}}}{{\text{E}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. {\frac{{{\dot{\text{K}}}}}{{\text{K}}}} \right]. $$
(74)
Using equations (68), (73) and (74), we have
$$\begin{aligned} &
\frac{{{\dot{\rm e}}}}{{\rm{e}}} = \frac{{\left\{ {{{\upmu }}\left( {1-\vartheta } \right)-1} \right\}\left( {\frac{{\left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)}}{{\left( {{{\upmu }}\left( {1-\vartheta } \right)-1} \right)}}\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \frac{{{\dot{\rm C}}}}{{\rm{C}}}} \right) + \frac{1}{\Delta }\left[ {-{{{\upvarepsilon }}_{\rm{E}}}\left\{ {-{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right.} \right.\left. { + {{{\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}\frac{{{\dot{\rm E}}}}{{\rm{E}}} + {{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\frac{{{\dot{\rm K}}}}{{\rm{K}}}} \right] + \frac{1}{\Delta }\left\{ {-{{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \left. {{{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{u}}}\frac{{{\dot{\rm K}}}}{{\rm{K}}}} \right\}} \right.}}{{\frac{{\rm{e}}}{{{\rm{V'}}\left( {\rm{e}} \right)}}{\rm{V}^{\prime\prime}}\left( {\rm{e}} \right)-\left( {\frac{{{\rm{p}^{\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{\left( {1-{\rm{p}}\left( {\rm{e}} \right)} \right)}} + \frac{{{\rm{p}^{\prime\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{{\rm{p}{\prime}}\left( {\rm{e}} \right)}}} \right)}},\\&
\mathop \Rightarrow \limits_{\rm{~}} \frac{{{\dot{\rm e}}}}{{\rm{e}}} = \frac{{\left\{ {{{\upmu }}\left( {1-\vartheta } \right)-1} \right\}\left( {\frac{{\left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)}}{{\left( {{{\upmu }}\left( {1-\vartheta } \right)-1} \right)}}\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \frac{{{\dot{\rm C}}}}{{\rm{C}}}} \right) + \frac{{{{{\upvarepsilon }}_{\rm{E}}}}}{\Delta }\left[ {\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right.\left. { + {{{\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\} + {{{\uptheta }}_{\rm{K}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right]\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \frac{1}{\Delta }{{{\uptheta }}_{\rm{K}}}\left( {{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\dot{\rm K}}}}{{\rm{K}}}}}{{\frac{{\rm{e}}}{{{\rm{V}^{\prime}}\left( {\rm{e}} \right)}}{\rm{V}^{\prime\prime}}\left( {\rm{e}} \right)-\left( {\frac{{{\rm{p}^{\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{\left( {1-{\rm{p}}\left( {\rm{e}} \right)} \right)}} + \frac{{{\rm{p}^{\prime\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{{\rm{p}^{\prime}}\left( {\rm{e}} \right)}}} \right)}}\;\quad \left[ {{\rm{with}~~\upsigma } = 1} \right],\\&
\mathop \Rightarrow \limits_{\rm{~}} \frac{{{\dot{\rm e}}}}{{\rm{e}}} = \frac{{\left\{ {{{\upmu }}\left( {1-\vartheta } \right)-1} \right\}\frac{{{\dot{\rm C}}}}{{\rm{C}}} + \frac{{{{{\upvarepsilon }}_{\rm{E}}}}}{\Delta }\left[ {\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right.\left. { + {{{\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\} + {{{\uptheta }}_{\rm{K}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}} + \left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)} \right]\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \frac{1}{\Delta }{{{\uptheta }}_{\rm{K}}}\left( {{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\dot{\rm K}}}}{{\rm{K}}}}}{{\frac{{\rm{e}}}{{{\rm{V'}}\left( {\rm{e}} \right)}}{\rm{V}^{\prime\prime}}\left( {\rm{e}} \right)-\left( {\frac{{{\rm{p}^{\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{\left( {1-{\rm{p}}\left( {\rm{e}} \right)} \right)}} + \frac{{{\rm{p}^{\prime\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{{\rm{p}^\prime}\left( {\rm{e}} \right)}}} \right)}}.\end{aligned}$$
(75)
Equation (76) is same as Eq. (27) in the body of the paper.
6.2 E.2 Stability of long-run equilibrium
While analysing stability of long run equilibrium, we use three independent equations of motion given by (24), (25) and (13). These equations of motion are given by
$$ \begin{aligned} & {\dot{\text{C}}} = \frac{{{\text{r}}\left( {1-{\uptau }} \right)-{\updelta }-{\uprho }}}{{1-{\upmu }\left( {1-\vartheta } \right)}}{\text{C}}-\frac{{\left( {1-{\upmu }} \right)\left( {1-\vartheta } \right)}}{{{\upmu }\left( {1-\vartheta } \right)-1}}{\text{C}}\frac{{{\dot{\text{E}}}}}{{\text{E}}}, \hfill \\ & \Rightarrow {\dot{\text{C}}} = \frac{{{\text{r}}\left( {1-{\uptau }} \right)-{\updelta }-{\uprho }}}{{1-{\upmu }\left( {1-\vartheta } \right)}}{\text{C}}-\frac{{\left( {1-{\upmu }} \right)\left( {1-\vartheta } \right)}}{{{\upmu }\left( {1-\vartheta } \right)-1}}\frac{{\text{C}}}{{\text{E}}}\left( {{{\uptau \text{rK}}}-{\upalpha \text{X}} + {\uppi \text{E}}} \right) \hfill \\ \end{aligned} $$
and
\(\begin{aligned}&{\dot{\text{K}}} = {\text{s}}\left( {{\text{X}}-{{\uptau \text{rK}}}} \right)-{{\updelta \text{K},}} \hfill \\ & \Rightarrow {\dot{\text{K}}} = \left( {1-\frac{{\text{C}}}{{{\text{X}}-{{\uptau \text{rK}}}}}} \right)\left( {{\text{X}}-{{\uptau \text{rK}}}} \right)-{\updelta \text{K}}. \hfill \\ & \mathop \Rightarrow \limits_{ } {\dot{\text{K}}} = {\text{X}}-{{\uptau \text{rK}}}-{\text{C}}-{{\updelta \text{K};}} \hfill \\ \end{aligned}\)
and
\({\dot{\text{E}}} = {{\uptau \text{rK}}}-{\upalpha \text{X}} + {\uppi \text{E}}\).
The stability properties of the long-run equilibrium depends on the sign of latent roots of the Jacobian matrix corresponding to those three equations of motion. The Jacobian matrix is given by.
\({\text{J}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}} \\ \end{array} } \right]\).
We assume \({\upsigma } = 1\), i.e., the production function is Cobb–Douglas. Using Eqs. (7A), (10A), (16)–(18) and long-run equilibrium conditions, we have
\( \begin{aligned} & \frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{c}}}} = 0; \\ & \frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{K}}}} = {\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} + \frac{{\left( {1-{\upmu }} \right)\left( {1-\vartheta } \right)}}{{{\upmu }\left( {1-\vartheta } \right)-1}}\frac{{\text{C}}}{{\text{E}}}\frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}; \\ & \frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{E}}}} =-{\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-\frac{{\left( {1-{\upmu }} \right)\left( {1-\vartheta } \right)}}{{{\upmu }\left( {1-\vartheta } \right)-1}}\frac{{\text{C}}}{{\text{E}}}\left\{ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)} \right\}; \\ & \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{C}}}} =-1 < 0; \\ & \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = \frac{{\text{X}}}{{\text{K}}}\frac{1}{\Delta }\left\{ {-{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{k}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right)} \right. + {\uptheta }_{{\text{K}}} \left. {{\upvarepsilon }_{{\text{u}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}-{\uptau \text{r}}\left( {1 + \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right)-{\updelta }; \\ & \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} =-\frac{{{\text{rK}}}}{{\text{E}}}\left( {1-{\uptau }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}} > 0; \\ & \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{C}}}} = 0; \\ & \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}} =-\frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} < 0 \\ & \text{and} \\ & \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = {\uppi }\frac{{\widehat{{{\text{pX}}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right) < 0. \end{aligned}\)
The determinant corresponding to this Jacobian matrix is given by
$$\begin{aligned} &
{\rm{Det}}\left( {\rm{J}} \right) = \left[ {{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)}}{{{{\upmu }}\left( {1-\vartheta } \right)-1}}\frac{{\rm{C}}}{{\rm{E}}}\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]\left[ {{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)} \right]\\&
-\left[ {{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}} + \frac{{\left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)}}{{{{\upmu }}\left( {1-\vartheta } \right)-1}}\frac{{\rm{C}}}{{\rm{E}}}\left\{ {{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)} \right\}} \right]\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
= {\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}\left[ {{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)} \right]\\&
-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
= {\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + {\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}\frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\\&
-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\&
= {\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}\frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\\&
-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{\vartheta }\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\\&
=-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right){{\uppi }}\left( {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}} \right)\\&
=-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right){{\uppi }}\left[ {\frac{1}{\Delta }\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right)} \right.} \right.\\&
+ {{{\uptheta }}_{\rm{K}}}\left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}\left. { + \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}} \right]\\&
=-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\uppi }}}{\Delta }\left[ {\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right)} \right.} \right.\\&
+ {{{\uptheta }}_{\rm{K}}}\left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}\left. { + {{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}} \right]\\&
=-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\uppi }}}{\Delta }\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right)} \right. + {{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{u}}} + \left. {{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}\\&
=-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\uppi }}}{\Delta }\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{K}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right)} \right. + \left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {{{{\uptheta }}_{\rm{K}}} + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}.\end{aligned}$$
When \({\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}} > {\upvarepsilon }_{{\text{u}}}\), \({\text{Det}}\left( {\text{J}} \right)\) is positive if \(\left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) > 0\); and we assume this to be true.
If the determinant of \({\text{J}}\) is positive, then either all three latent roots are positive or two roots are negative and one root is positive.
Trace of the Jacobian matrix is given by
$$ \begin{aligned} & {\text{Tr}}\left( {\text{J}} \right) = \frac{{\text{X}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}-{\tau r}\left( {1 + \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right)-{\updelta } + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right) \hfill \\ &= \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\left( {\frac{{\text{X}}}{{\text{K}}} + {\uppi }} \right)-{\tau r}\left( {1 + \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right)-{\updelta } + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right) \hfill \\ &= \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\left( {\frac{{\text{X}}}{{\text{K}}} + {\uppi }} \right)-{\tau r}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}}-\frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}}-{\tau r}-{\updelta } + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}} \hfill \\& = \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\left( {\frac{{\text{X}}}{{\text{K}}} + {\uppi }} \right)-\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \left( {{\tau r} + {\uppi }} \right)-{\tau r}-{\updelta } + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}} \hfill \\ \end{aligned} $$
Here \(\left\{ {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\left( {\frac{{\text{X}}}{{\text{K}}} + {\uppi }} \right)-\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \left( {{\uptau \text{r}} + {\uppi }} \right)} \right\} > 0 \,{\text{and}}\, \left\{ {-{\uptau \text{r}}-{\updelta } + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right\} < 0\). So, Trace of the Jacobian matrix is indeterminate in sign.
In order to determine the sign of the latent roots of the \({\text{J}}\) matrix we apply the Routh-Hurwitz Theorem. The characteristic equation obtained from \({\text{J}}\) matrix is given by
$$ - {{\rm{v}}^3} + {\rm{Tr}}\left( {\rm{J}} \right){{\rm{v}}^2} - {\rm{M}}\left( {\rm{J}} \right){\rm{v}} + {\rm{Det}}\left( {\rm{v}} \right) = 0,$$
(76)
where \({\text{v}}\) is the latent root.
Here,
$$ {\text{M}}\left( {\text{J}} \right) = \left\lceil {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{c}}}}} & {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{K}}}}} \\ {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}}} \\ \end{array} } \right\rceil + \left\lceil {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}} \\ \end{array} } \right\rceil + \left\lceil {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{c}}}}} & {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}} \\ \end{array} } \right\rceil $$
The sign of \({\text{M}}\left( {\text{J}} \right)\) is ambiguous.
The number of positive roots in the characteristic equation (72) is equal to the number of variations of signs in the scheme
$$ \left\{ { - 1,{\text{ Tr}}\left( {\text{J}} \right), - {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}},{\text{Det}}\left( {\text{J}} \right)} \right\}. $$
(77)
If the sign of \({\text{M}}\left( {\text{J}} \right)\) is ambiguous, then sign of \(- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}\) is also ambiguous. Hence the number of positive latent roots can not be obtained in this way.
The number of negative roots will determine the nature of transitional paths around the long-run equilibrium point. In this model, we have two state variables, \({\text{K}}\) and \({\text{E}}\), and only one control variable, \({\text{C}}\). The properties of transitional dynamics depends on the relationship between the number of state variables and the number of negative latent roots. The long run equilibrium is saddle point stable (unstable) if the number of negative latent roots is equal to (less than) the number of state variables. However, it faces indeterminacy with infinite number of transitional path when number of negative latent roots is greater than the number of state variables.Footnote 27 We consider four alternative cases.
Case (i): Trace is positive and \(- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}\) is positive.
We have only one variation in sign in the scheme (76) in this case. So the characteristic equation (77) has only one positive root and two negative roots; and thus the number of negative latent roots is equal to the number of state variables. Hence the long-run equilibrium point satisfies saddle point stability in this case.
Case (ii): Trace is positive and \(- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}\) is negative.
We have three variations in sign in the scheme (76). So the characteristic equation (77) has all three positive latent roots. So the number of negative latent roots being zero falls short of the number of state variables. So the long-run equilibrium is unstable in this case.
Case (iii): Trace negative and \(- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}\) is positive.
We have only one variation in sign in the scheme (76) in this case. So the characteristic equation (77) has only one positive root and two negative roots; and thus the number of negative latent roots is equal to the number of state variables. Hence the long-run equilibrium point satisfies saddle point stability in this case.
Case (iv): Trace negative; \(- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}\) is negative.
We have only one variation in sign in the scheme (76) in this case. So the characteristic equation (77) has only one positive root and two negative roots; and thus the number of negative latent roots is equal to the number of state variables. Hence the long-run equilibrium point satisfies saddle point stability in this case.
6.3 E.3 Comparative steady state effects
We analyse comparative steady state effects on \({\text{K}}\), \({\text{E}}\) and \({\text{u}}\) with respect to change in \({\uptau }\) when the equilibrium is saddle point stable. \({\text{C}}\) is a jump variable; and its value can be thrown on the saddle path.
From Eq. (24), i.e., with \({\dot{\text{C}}} = 0\) and \({\dot{\text{E}}} = 0\), we have
$$ {\text{C}}\frac{{\left( {1 - {\uptau }} \right)}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \frac{{{\text{dK}}}}{{{\text{d}\uptau}}} - {\text{C}}\frac{{\left( {1 - {\uptau }} \right)}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}\frac{{\text{r}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = \frac{{{\text{rC}}}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}. $$
(78)
From Eq. (13), with \({\dot{\text{E}}} = 0\), we have
$$ - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} + \left\{ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)} \right\}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}{.} $$
(79)
Using equations (79) and (80), we have
$$ \begin{gathered} \frac{{{\text{dK}}}}{{{\text{d}\uptau }}} =-\frac{{{\text{rC}}\frac{1}{{1-{\upmu }\left( {1-\vartheta } \right)}}\left[ {\left\{ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)} \right\}-{\text{K}}\left( {1-{\uptau }} \right)\frac{{\text{r}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right]}}{{{\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)\frac{{\uppi }}{\Delta }\left\{ {-{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right)} \right. + \left. {{\upvarepsilon }_{{\text{u}}} \left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}}} \hfill \\ \mathop \Rightarrow \limits_{ } \frac{{{\text{dK}}}}{{{\text{d}\uptau}}} =-\frac{{{\text{rC}}\frac{1}{{1-{\upmu }\left( {1-\vartheta } \right)}}\left[ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}\frac{1}{\Delta }\frac{1}{{\text{E}}}\left\{ {{\uppi \text{E}}-\left( {1-{\uptau }} \right){\text{rK}}} \right\}} \right]}}{{{\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)\frac{{\uppi }}{\Delta }\left\{ {-{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right)} \right. + \left. {{\upvarepsilon }_{{\text{u}}} \left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}}} \hfill \\ \mathop \Rightarrow \limits_{ } \frac{{{\text{dK}}}}{{{\text{d}\uptau}}} =-\frac{{{\text{rC}}\frac{1}{{1-{\upmu }\left( {1-\vartheta } \right)}}\left[ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}\frac{1}{\Delta }\frac{1}{{\text{E}}}\left\{ {{\uppi \text{E}}-\left( {{\updelta } + {\uprho }} \right){\text{K}}} \right\}} \right]}}{{{\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)\frac{{\uppi }}{\Delta }\left\{ {-{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right)} \right. + \left. {{\upvarepsilon }_{{\text{u}}} \left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}}}; \hfill \\ \end{gathered} $$
(80)
and
$$ \frac{{{\text{dE}}}}{{{\text{d}\uptau}}} =-\frac{{{\text{rC}}\frac{1}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}\left[ {\frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - {\text{K}}\left( {1-{\uptau }} \right)\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right]}}{{{\text{C}}\frac{{\left( {1 - {\uptau }} \right)}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)\frac{{\uppi }}{\Delta }\left\{ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)} \right. + \left. {{\upvarepsilon }_{{\text{u}}} \left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}}}. $$
(81)
For both equation (80) and (81) denominators in the RHS are negative if \(\left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) > 0\) and \({\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)\). Numerator of (81) is always positive. Numerator of (81) is positive if \({\uppi \text{E}} < \left( {{\updelta } + {\uprho }} \right){\text{K}}\). Hence, under these conditions, \(\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} > 0\) and \(\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} > 0\).
Using equation (60), we obtain
$$ \frac{{{\text{du}}}}{{{\text{d}\uptau }}} = \frac{{\text{u}}}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\upsigma \text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\frac{1}{{\text{E}}}\frac{{{\text{dE}}}}{{{\text{d}\uptau }}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. {\frac{1}{{\text{K}}}\frac{{{\text{dK}}}}{{{\text{d}\uptau }}}} \right]. $$
(82)
Here also \(\frac{{{\text{du}}}}{{\text{d}\uptau }} < 0\), as \(\frac{{{\text{dE}}}}{{{\text{d}\uptau }}} > 0\) and \(\frac{{{\text{dK}}}}{{{\text{d}\uptau }}} > 0\).
Appendix F
If we assume full employment in the model of the body of the paper; then term \({\upvarepsilon }_{\mathrm{u}}=0\). Then, without using Solow (1979) condition i.e. assuming that \({\upvarepsilon }_{{\text{w}}} \ne 1\), Eqs. (28), (29), (32) and (33) are modified as follows
$$ {\uptheta }_{{\text{L}}} {\hat{\text{w}}} - {\uptheta }_{{\text{L}}} {\hat{\text{e}}} + {\uptheta }_{{\text{K}}} {\hat{\text{r}}} = 0; $$
(83)
$$ {\upvarepsilon }_{{\text{w}}} {\hat{\text{w}}} - {\hat{\text{e}}} = - {\upvarepsilon }_{{\text{E}}} {{\hat{\text{E}}}} ;$$
(84)
$$ {\uptheta }_{{\text{L}}} {{\upsigma \hat{\text{W}}}} - {\uptheta }_{{\text{L}}} {{\upsigma \hat{\text{e}}}} - {\uptheta }_{{\text{L}}} {{\upsigma \hat{\text{r}}}} + {\hat{\text{X}}} = {{\hat{\text{K}};}} $$
(85)
and
$$ - {\uptheta }_{{\text{K}}} {{\upsigma \hat{\text{W}}}} - \left( { - {\uptheta }_{{\text{K}}} {\upsigma } + 1} \right){\hat{\text{e}}} + {\uptheta }_{{\text{K}}} {{\upsigma \hat{\text{r}}}} + {\hat{\text{X}}} = 0. $$
(86)
From Eqs. (83), (84), (85) and (86), we have
$$ \Delta = {\upsigma } + {\upvarepsilon }_{{\text{w}}} \left\{ { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right\}. $$
(87)
Following equations describe the flexible wage full employment model with exogenous labour efficiency.
$$ 1 = {\text{a}}_{{\text{L}}} {\text{w}} + {\text{a}}_{{\text{K}}} {\text{r}}{.} $$
(88)
$$ {\text{a}}_{{\text{K}}} {\text{X}} = {\text{K}}{.} $$
(89)
$$ {\text{a}}_{{\text{L}}} {\text{X}} = {\text{L}}{.} $$
(90)
Here \({\upvarepsilon }_{{\text{w}}} = 0\); and hence from Eq. (87) we have
$$ \Delta = {\upsigma }{.} $$
(91)