Private versus public companies with strategic CSR

Abstract

We analyze the effects of strategic Corporate Social Responsibility (CSR) on social welfare in an industry where firms are owned by consumers (publicly owned) and CSR commitment takes the form of a fraction of the consumer surplus into the firms’ objective function. We compare this market configuration with the standard case of firms owned by entrepreneurs (privately owned). In line with the empirical evidence, consumers’ ownership gives an incentive to adopt a socially responsible, welfare improving statute. While privately-owned companies are limited in the level of social concern to implement, publicly-owned companies are not, and CSR is welfare-improving for any level of social concern. Surprisingly, a market configuration of publicly-owned CSR companies decreases welfare compared to an oligopoly of privately-owned CSR companies. The analysis is then extended by considering asymmetric oligopolies with different company types.

1 Introduction

The last two decades have seen Corporate Social Responsibility (CSR) become a central topic in the corporate world and business reporting. A growing number of corporations have implemented CSR activities: in 2017, more than 60% of the firms in all industry sectors now report on CSR all over the world, with 83% in the Americas region, 78% in the Asia Pacific region, 77% in Europe and 52 % in Africa (KPMG 2017).

An increasing interest for CSR has characterized the economic literature in the past years. Several approaches to the definition of CSR and why firms engage in CSR activities have been proposed. In general, two types of CSR activities are identified: not-for-profit and strategic CSR (Kitzmueller and Shimshack 2012). The former refers to CSR decisions as private (corporate) provision of public goods (Bagnoli and Watts 2003; Kotchen 2006; Besley and Ghatak 2010). The latter refers to the fact that CSR practices affect the interaction between firms and stakeholders, such as socially or environmentally concerned consumers, political activists, employees, and competitors.

Our focus is on the role of imperfect competition, which has brought substantial developments in the analysis of strategic CSR. Some relevant contributions in a static framework are Goering (2008a, 2008b, 2010), Kopel and Brand (2012), Lambertini and Tampieri (2015), among others. This literature shows that, in general, firms may strategically commit to CSR activities to obtain higher profits than their profit-seeking competitors.

A typical feature of that strand of literature is the tacit assumption that firms are “ privately” held by a small number of shareholders, who are not willing to go public (offering shares). While modelling firms as private companies is often the relevant configuration of firms’ ownership, it is not, however, the only possible configuration, given the presence of “ public” companies whose ownership is divided into shares of stock held by consumers/savers.¹ Examples of large public companies are Apple, Shell and Wells Fargo (Forbes 2019). A different structure of company ownership entails different business objectives. Managers of public companies have, then, more than an incentive to maximize shareholders wealth, in line with the CSR modelling in the management literature (Mc WiIlliams and Siegel 2001). The empirical evidence supports this view. A large bulk of literature shows that publicly held firms are more likely to engage in socially responsible activities (Lee 2009; Tagesson et al. 2009; Lourenço and Branco 2013), which comes with no surprise since their funding depends, at least in part, on the investor base.

Setting aside the variety of the incentives that give rise to CSR (Benabou and Tirole 2010), standard theory on CSR generally assumes a clear distinction between consumers and firms, where the latter are owned by entrepreneurial agents (privately-owned firms). This approach cannot be extended to the case where a large number of shareholders (the consumers) play a crucial role in targeting the business behavior (publicly-owned firms). As a result, what welfare scenarios may arise from publicly-owned firms engaging CSR activities remain unclear, and so are also the welfare effects of strategic interaction between competitors differentiated by ownership structure and CSR engagement.

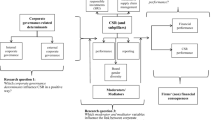
In this paper, we provide an answer to these issues by studying the welfare effects of a CSR oligopoly of privately-owned vis à vis publicly-owned companies.

The first part of the analysis focuses on symmetric markets, which is our baseline model. We compare the level of welfare when the underlying oligopoly is composed of socially responsible firms with the level of welfare when the oligopoly is composed of standard profit-seeking firms. Our analysis is assessed on two different firm ownership structures, privately-owned and public-owned firms.

As a starting point, we assume that the oligopoly is composed of privately-owned companies, and we compare the two alternative cases where all firms are either profit seeking or socially responsible. Socially responsible behavior is introduced in the form of a modified objective function of the firms which, in this case, are assumed to maximize profits plus an exogenously given weight of consumer indirect utility (or consumer surplus). We show that the outcome resulting from a socially concerned oligopoly leads to a decrease of the general price level and profits and an increase of the quantity of the consumption good produced, consumer surplus, and social welfare. The economic intuition is straightforward. If the objective function of the firms includes consumer surplus, besides profits, then prices are lower than those that arise when the objective function of firms contains profits, only. As a result, the quantity of the consumption good produced increases. However, the decrease of profits entails that there are no incentives to engage in welfare-enhancing CSR activities when the oligopoly is composed of privately-owned firms.

Next, we show that this result does not hold when consumers own the industry, so that each firm is in fact publicly owned. In this configuration, consumers enjoy a share of dividends as part of their income. Adopting a CSR statute still lowers profits and thus their dividends, but the gain in terms of consumer surplus from lower prices more than offsets the profit loss. This consumers-driven incentive puts pressure on the firms’ governance and justifies a CSR market configuration, which ultimately raises social welfare. In addition, while privately-owned companies are willing to implement only a low level of social concern, which is inversely proportional to the number of firms in the oligopoly, publicly-owned companies, conversely, have more than incentive to commit themselves to any level of social concern. To understand why, notice that, when CSR is engaged by public companies, social concern implies also concern towards what consumers own, that is, companies shares. This, in turn, entails that the CSR objective function, in this case, always allows for positive equilibrium profits.

Finally, an oligopoly composed of publicly-owned CSR firms is welfare-improving with respect to an oligopoly composed of publicly-owned profit-seeking firms but, quite surprisingly, not with respect to an oligopoly composed of privately-owned CSR firms. In this case indeed, equilibrium quantities are set at a lower level than in the case of privately-owned CSR firms, suggesting that the socially concerned effort is stronger in private companies. This result is again related to the fact that publicly-owned CSR firms take into account the consumers’ ownership, that is, the earnings from consumers’ shares. However, for high levels of social concern, a market configuration based on privately-owned CSR firms may not be implemented since profits may be negative. Conversely, a market configuration based on publicly-owned CSR firms remains still possible and is welfare-enhancing with the increase of the level of social concern. To this respect, we evaluate the condition to reach the Pareto Optimum, whenever possible.

The second part of the analysis focuses on asymmetric markets, that is, industry configurations composed of different company types, differentiated by either the ownership structure or the production strategy. We start by considering an industry configuration which includes all types of companies (privately-owned CSR firms, privately-owned profit-seeking firms, publicly-owned CSR firms, publicly-owned profit-seeking firms). Here, we first study the stability of the industry configuration to verify whether there exist the conditions such that no company, either publicly-owned or privately-owned, has an incentive to switch production strategy, CSR or profit-seeking. Our findings show that, unless CSR requires specific investment costs, a market configuration with all types of companies is unstable. Then, we study the stable asymmetric oligopolies. These are composed of (i) publicly-owned CSR companies and privately-owned profit-seeking companies or (ii) of publicly-owned and privately-owned companies, both with a CSR production strategy. For each market configuration, we evaluate the effects of an endogenous CSR commitment, determined either by the government or the CSR company.

There exists a large body of literature that has studied how consumer ownership and production strategies affect firm behavior and equilibrium outcomes. Although with a different aim and approach, our paper is related to the literature of mixed oligopoly (De Fraja and Delbono 1989; Fershtman and Judd 1987; Corneo and Jeanne 1992) and the literature of consumer ownership (Farrell 1985; Mas-Colell and Silvestre 1989, 1991; Corneo 1997). Our model departures from these earlier papers in two main aspects. First, our analysis adopts a general equilibrium approach, which allows us to disclose the price mechanism behind the trade-off between social welfare and profits in different production objectives, CSR and profit-seeking. Second, we do not focus on price discrimination, but, rather, on the final effects of CSR activities on social welfare, and we conduct this analysis for different market structures, private and public. Our study shows that, in a market structure of public companies, CSR activities are welfare-enhancing compared to profit-seeking activities, for any level of social concern. Most importantly, we show that CSR activities lead to Pareto optimum only in a market structure of private companies.

Our results are also related to those in Planer-Friedrich and Sahm (2020), who study strategic CSR in imperfectly competitive markets. Although we use a different approach, we share with their model the finding that private companies always choose a positive level of CSR and such a degree of concern is decreasing with the number of companies in the market. However, Planer-Friedrich and Sahm (2020) study the interplay between CSR concern and market structure (concentration), while we study the interplay between CSR and ownership structure (private or public).

The rest of the paper is organized as follows. Section 2 describes the model. Section 2.1 analyzes and compares the results in the different oligopoly configurations in terms of ownership structure and production behavior. Section 3 endogenizes the market structure, with a focus on the two stable market configurations. Section 4 concludes.

2 The model

2.1 Demand side

Consider an economy with a finite number of consumers $i \in \{ 1,2,\ldots ,h\}$, and a finite number of firms $j\in \left\{ 1,2,\ldots ,n\right\}$, which produce a final good y. Consumers have the same endowment of available time L they can use to rest or work; $l_i$ denotes the leisure time and $l_i^{s}:=L-l_{i}$ is the supply of labor. Each consumer’s utility depends on leisure and the consumption of y.² Consumers’ preferences are represented by the following utility function

$$\begin{aligned} U_{i}:\mathbb {R}^{2}\rightarrow \mathbb {R},\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ U_{i}\left( y_{i},l_{i}\right) =ay_{i}-\frac{1}{2}y_{i}^{2}+l_{i}. \end{aligned}$$

(1)

Labor is sold at the wage rate w which is normalized to 1, so that individual wage earnings are given by $wl_{i}^{s}=l_{i}^{s}$. In the standard approach, where firms are privately owned, this is the only source of income, since it is assumed that firms belong to a negligible number of individuals (“entrepreneurs”), whose consumption’s behavior is not modelled for simplicity.

If conversely firms are owned by consumers, as with the case of a public company, each consumer i owns a fixed share of each firm j, denoted by $\alpha _{ij}\in \left[ 0,1\right]$, with $\sum _{i}\alpha _{ij}=1$, for all $j=1,\ldots ,n$. The amount of dividends obtained by consumer i from firm j is then $\alpha _{ij}\pi _{j}^{\sigma }$, where $\pi _{j}^{\sigma }$ represents firm j’s profits when production takes place under the production behavior $\sigma \in \{ps,sr\}$, which is discussed in details in the next section.³ Let $\omega \in \{pr, pub\}$ be an index referring to the firms ownership structure, private (pr) or public (pub ). The total profit owned by consumer i is $\Pi _{\omega ,i}^{\sigma }:=\sum \nolimits _{j=1}^{n}\alpha _{ij}\pi _{j}^{\sigma } \mathbf {1}_{ \left\{ \omega =pub \right\} }$, where the indicator function $\mathbf {1}_{ \left\{ \omega =pub \right\} }$ takes value 1 if $\omega =pub$ and 0 otherwise. If the firms ownership is private, then consumer i’s income is composed of her supply of labor only. If the firms’ ownership is public, besides the labor income, consumer i can rely on firms’ profits, which, in turn, depend on the production behavior $\sigma$.

Therefore, consumer i’s problem can be represented as follows:

$$\begin{aligned}&\max _{(y_{i},l_{i})}U_{i}(y_{i},l_{i}) \\ &\text {s.t.}\,py_{i}+l_{i}\le L+\Pi _{\omega ,i}^{\sigma }. \end{aligned}$$

(2)

Solution of (2) (see Appendix A for details) yields the individual demand for good y and leisure:

$$\begin{aligned} y_{i}=a-p,\qquad l_{i}=L+\Pi _{\omega ,i}^{\sigma }-p\left( a-p\right) . \end{aligned}$$

Notice that $y_{i}$ is the usual linear demand function for homogeneous goods, and it is constant across consumers. Then, overall demand is

$$\begin{aligned} y=hy_{i}=h\left( a-p\right) , \end{aligned}$$

so that the inverse of the demand function is

$$\begin{aligned} p=a-\frac{y}{h}. \end{aligned}$$

2.2 Supply side

Let $y_{j}$ be the quantity of the final good produced by firm $j\in \left\{ 1,..,n\right\}$. Technology is as follows: $c\in \left( 0,1\right)$ units of labor are needed to produce 1 unit of the final good. We make the following assumption.

Assumption 1

Each firm assumes the demand function she faces is $p=a-\frac{y}{h}$.

We can interpret this as a “ Cournot-Walras” model in a general equilibrium setting (Codognato and Gabszewicz 1991; Gabszewicz and Michel 1997): firms assume that prices are such that market clears, i.e., total demand = total supply, i.e., $h\left( a-p\right) =y$. Letting $y_{-j}:=\sum _{j^{\prime }\ne j}y_{j^{\prime }}$, therefore, the demand function can be rewritten as

$$\begin{aligned} \ y_{i}=a-p=\frac{y_{j}+y_{-j}}{h}. \end{aligned}$$

(3)

Inverse demand is thus

$$\begin{aligned} p=a-\frac{y_{j}+y_{-j}}{h}\text {,} \end{aligned}$$

(4)

equilibrium labor is

$$\begin{aligned} l_{i}=L+\Pi _{\omega ,i}^{\sigma }-\left( a-\frac{y_{j}+y_{-j}}{h}\right) \frac{y_{j}+y_{-j}}{h}, \end{aligned}$$

(5)

and firm j’s profit is

$$\begin{aligned} \pi _{j}^{\sigma }=\left( p-c\right) y_{j}=\left( a-\frac{y_{j}+ y_{-j}}{h} -c\right) y_{j}. \end{aligned}$$

Each firm may operate under two mutually exclusive production behaviors, $\sigma \in \{ps,sr\}$. In the first case, the firm is profit-seeking (ps), that is, it maximizes profits by competing in quantities. In the second case, the firm is socially responsible (sr), that is, it maximizes profits and a share of consumer surplus, which amounts to total indirect utility. Firm j’s behavior is identified by the following objective function:

$$\begin{aligned} o_{j}^{\sigma }=\pi _{j}^{\sigma }+zCS^{\sigma }\cdot \varvec{1}_{\{\sigma =sr\}},\qquad \text {with }\sigma \in \{ps,sr\}, \end{aligned}$$

(6)

where $CS_{\omega }^{\sigma }=\sum _{i=1}^{h}V_{\omega ,i}^{\sigma }$ is the consumer surplus, defined as the sum of the indirect utilities $V_{\omega ,i}^{\sigma }$, while $z\in \left( 0,1\right)$ represents the level of CSR activities engaged by firm j, corresponding to a certain share of consumer surplus. Notice that maximizing $o_{j}^{sr}$ is equivalent to maximizing $\frac{1}{1+z}\pi _{j}+\frac{z}{1+z}CS$, with $z\in \left( 0,1\right]$, i.e., a convex combination of profits and consumer surplus.⁴

3 Symmetric markets

In this section, we outline the results in the baseline case where all firms are homogeneous, that is, they all have the same production strategy and the same ownership structure. This setting allows us then to compare the different market equilibria and the effects on welfare. The section is organized as follows: we first consider the standard case where oligopolists are private companies ($\omega =pr$). We next analyze the oligopoly composed by public companies ($\omega =pub$). For each case, we compare the two alternative production behaviors “ profit-seeking” ($\sigma =ps$) and “socially responsible” ($\sigma =sr$), and we discuss the implications in terms of welfare. In each of these economies, the results are derived in three steps:

• 1. We compute aggregate demand and aggregate supply;

• 2. We equate them to calculate the equilibrium price, and, in turn, the individual demand of consumers and the individual supply of firms (in the case of oligopolists);

• 3. Finally, we derive the value of profits and welfare at the equilibrium price.

Before proceeding with the analysis, we define social welfare as

$$\begin{aligned} W_{\omega }^{\sigma }:= {\left\{ \begin{array}{ll} CS^{\sigma }_{\omega }+\sum _{j=1}^n\pi _{j}^{\sigma }, &{} \qquad \text {if } \omega =pr, \\ CS^{\sigma }_{\omega }, &{} \qquad \text {if } \omega =pub. \end{array}\right. } \end{aligned}$$

Notice that $W^{\sigma }_{\omega }$ differs according to the ownership structure of the industry, $\omega \in \{pr,pub\}$. This is so because, if $\omega =pub$, profits enter the consumer’s problem through the budget constraint.

3.1 Private companies

Consider an oligopoly composed of privately-owned firms, that is, $\omega =pr$ . This is the implicit assumption adopted in the literature of strategic CSR, and implies a separation between consumers and firms. A possible interpretation is that each firm is owned by a capitalist family.

3.1.1 Profit-seeking production strategy

Consider first companies that adopt the profit-seeking production strategy, therefore $(\omega , \sigma )=(pr,ps)$. Each firm j faces the following problem. For given $a\in \mathbb {R}_{++},\sum y_{-j}$ and $c\in \left( 0,1\right)$.

$$\begin{aligned} \begin{array}{ll} \max _{y_{j}\in \mathbb {R}}\left( a-\frac{y_{j}+\sum y_{-j}}{h}-c\right) y_{j} \text { \ \ \ \ \ \ \ \ s.t. \ }&y_{j}\ge 0. \end{array} \end{aligned}$$

(7)

This is the standard Cournot problem with n firms: it is straightforward to show that, if $h\left( a-c\right) >\sum _{j^{\prime }\ne j}y_{j^{\prime }}$, then Problem (7) has the reaction function

$$\begin{aligned} y_{j}=\frac{h\left( a-c\right) -\sum y_{-j}}{2}. \end{aligned}$$

The unique symmetric Nash equilibrium is

$$\begin{aligned} y_j:=y_{pr}^{ps}=\frac{h\left( a-c\right) }{1+n},\qquad j\in \left\{ 1, \ldots ,n\right\} \end{aligned}$$

where pr and ps refer to an industry composed of private profit-seeking companies, only.

By plugging $y_{pr}^{ps}$ into the equilibrium quantities, we get that the equilibrium price, profits, indirect utility and welfare are:

$$\begin{aligned} \begin{array}{ll} p:=p_{pr}^{ps}=a-\frac{n\left( a-c\right) }{1+n}, &{} \\ \pi _{j}^{ps}:=\pi _{pr}^{ps}=\frac{h\left( a-c\right) ^{2}}{\left( 1+n\right) ^{2}}, &{} \quad j=1,\ldots ,n \\ V_{pr,i}^{ps}:=V_{pr}^{ps}=\frac{1}{2}\left[ \frac{n\left( a-c\right) }{1+n} \right] ^{2}+L, &{} \quad i=1,\ldots ,h \\ W_{pr}^{ps}=n\frac{h\left( a-c\right) ^{2}}{\left( 1+n\right) ^{2}}\frac{n+2 }{2}+hL. &{} \end{array} \end{aligned}$$

(8)

3.1.2 Socially responsible production strategy

Consider now companies that adopt the socially responsible production strategy, therefore $(\omega ,\sigma )=(pr,sr)$. Each firm j faces the following problem. For given $a\in \mathbb {R}_{++},\sum y_{-j}$ and $c\in \left( 0,1\right)$,

$$\begin{aligned} \max _{y_{j}\in \mathbb {R}}\left( a-\frac{y_{j}+\sum y_{-j}}{h}-c\right) y_{j}+z\left[ \frac{h}{2}\left( \frac{y_{j}+\sum y_{-j}}{h}\right) ^{2}+hL \right] . \end{aligned}$$

Maximizing with respect to $y_{j}$ yields:

$$\begin{aligned} \frac{\partial o_{j}^{sr}}{\partial y_{j}}=0\quad \Leftrightarrow \quad h\left( a-c\right) -2y_{j}-\sum y_{-j}+z\left( y_{j}+\sum y_{-j}\right) =0. \end{aligned}$$

Then, the reaction function is

$$\begin{aligned} y_{j}=\frac{h\left( a-c\right) }{2-z}-\frac{1-z}{2-z}\sum y_{-j}, \end{aligned}$$

with higher intercept and gentler slope than the case of profit-seeking firms, since

$$\begin{aligned} \frac{1-z}{2-z}<\frac{1}{2}\text { for }z\in \left( 0,1\right) \text {.} \end{aligned}$$

The symmetric solution is

$$\begin{aligned} y_{pr}^{sr}=\frac{h\left( a-c\right) }{1+n\left( 1-z\right) }. \end{aligned}$$

Using the definition of $y_{pr}^{sr}$, the elements of market equilibrium are given by:

$$\begin{aligned} \begin{array}{ll} p:=p_{pr}^{sr}=a-\frac{n\left( a-c\right) }{1+n\left( 1-z\right) }>0, &{} \text { if }z\in \left( 0,\frac{a+cn}{an}\right) \\ \pi _{j}^{sr}:=\pi _{pr}^{sr}=\frac{h\left( 1-nz\right) \left( a-c\right) ^{2}}{\left[ 1+n\left( 1-z\right) \right] ^{2}}>0, &{} \text {if }z\in \left( 0, \frac{1}{n}\right) ,\quad j=1,\ldots ,n \\ V_{pr,i}^{sr}:=V_{pr}^{sr}=\frac{1}{2}\frac{n^{2}\left( a-c\right) ^{2}}{ \left[ 1+n\left( 1-z\right) \right] ^{2}}+L, &{} i=1,\ldots ,h \\ W_{pr}^{sr}=hV_{pr}^{sr}+n\pi _{pr}^{sr}=n\frac{h\left( a-c\right) ^{2}}{ \left[ 1+n\left( 1-z\right) \right] ^{2}}\left( \frac{2+n-2nz}{2}\right) +hL. &{} \end{array} \end{aligned}$$

(9)

Notice that $\frac{1}{n}<\frac{a+cn}{an}$ and

$$\begin{aligned} n\frac{h\left( a-c\right) ^{2}}{\left[ 1+n\left( 1-z\right) \right] ^{2}} \left( \frac{n+2-2nz}{2}\right) >0\quad \text { if }\quad z\in \left( 0,\frac{ n+2}{2n}\right) , \end{aligned}$$

where $\frac{n+2}{2n}>\frac{1}{n}$. Therefore, condition $z<\frac{1}{n}$ is sufficient to ensure positive prices, profits and social welfare obtained by the market of goods. This restriction on z has the following explanation. Necessarily, there is a trade-off between profits and consumer surplus, since the former is larger with a low output, while the latter is larger with a high output. Therefore, for sufficiently large z, the weight of consumer surplus brings about an equilibrium output so low that profits become negative.

3.1.3 Welfare comparison

We are now in a position to compare the two production strategies when companies are privately owned. The results are summarized in the following proposition.

Proposition 1

Consider an oligopoly composed of private companies. If $z< \frac{1}{n}$, then output, consumer surplus and social welfare are higher, while profits and price are lower, in the case of CSR configuration compared to the case of profit-seeking configuration. That is,

$$\begin{aligned} y_{pr}^{ps}< y_{pr}^{sr}, \qquad p_{pr}^{ps}> p_{pr}^{sr}, \qquad V_{pr}^{ps}<V_{pr}^{sr}, \qquad \pi _{pr}^{ps}>\pi _{pr}^{sr}, \qquad W_{pr}^{ps}<W_{pr}^{sr}. \end{aligned}$$

Proof

The results immediately follow by comparing the equilibrium quantities in (8) with those in (9).□

A quick glance is sufficient to compare equilibrium outputs, prices and consumer surpluses in the two production strategies. The comparison of profits and social welfare is less immediate. In particular, regarding the social welfare, we have

$$\begin{aligned} W_{pr}^{ps}-W_{pr}^{sr}<0 \quad \text {if} \quad z<\frac{2n+2}{n\left( 2+n\right) }. \end{aligned}$$

Noting that $\frac{1}{n}<\frac{2n+2}{n(2+n)}$, it follows that under the condition $z<\frac{1}{n}$ welfare is always higher in a socially responsible oligopoly if firms are privately owned.

The intuition behind the social welfare improvement is straightforward: since a socially responsible firm takes into account also consumers’ welfare, it chooses a higher output level, and, in turn, a lower price, than a profit-seeking firm would do. Proposition 1 is in line with the results of the literature on strategic CSR: since profits are lower in the case of CSR, there are no private incentives to reach a market configuration of an oligopoly composed of all privately-owned CSR firms, even though such a configuration would be socially desirable. As noticed above, the implicit assumption adopted in this literature is that firms are private companies. In the next section, we will study whether the conflict between private and social incentives applies also to an oligopoly composed of publicly-owned firms.

It is also worth noting that, as the number of firms n increases, the condition under which a CSR production strategy is feasible $\left( z< \frac{1 }{n}\right)$ narrows down: in perfectly competitive market, as $n\rightarrow \infty$, firms would all set $z=0$. Conversely, in the case of monopoly ($n=1$), the CSR production strategy yields a welfare improving outcome compared to the profit seeking production strategy, for all $z\in \left( 0,1\right)$. Hence, the following result holds.

Corollary 1

The welfare gain due to a CSR production behavior increases with firms’ market power.

3.2 Public companies

Consider now an oligopoly composed of publicly-owned firms, that is $\omega =pub$. In a public company, the consumer’s budget is given not only by labor income, but also by the share of dividends, since, in this case, consumers hold the firms (see (2), for $\omega =pub$).

3.2.1 Profit-seeking production strategy

Start by considering companies that adopt the profit-seeking production strategy, therefore $(\omega , \sigma )=(pub,ps)$. In this case, output, price, profits, and social welfare in equilibrium are the same as the case with private, profit-seeking companies. This is so because the inverse demand function remains unchanged in the two market structures, therefore the firm’s problem yields the same solution:

$$\begin{aligned} y_j:=y_{pr}^{ps}=y_{pub}^{ps}=\frac{h\left( a-c\right) }{1+n}. \end{aligned}$$

Plugging the expression for $y_{pub}^{ps}$ into prices, indirect utility, and profits yields:

$$\begin{aligned} \begin{array}{ll} p:=p_{pub}^{ps}=a-\frac{n\left( a-c\right) }{1+n}, &{} \\ \pi _j^{ps}:=\pi _{pub}^{ps}=\frac{h\left( a-c\right) ^{2}}{\left( 1+n\right) ^{2}}, &{} \quad j=1,\ldots ,n \\ V_i^{ps}:=V_{pub}^{ps}=n\frac{\left( a-c\right) ^{2}}{\left( 1+n\right) ^{2}} \frac{n+2}{2}+L, &{} \quad i=1,\ldots ,h \\ W_{pub}^{ps}:=hV_{pub}^{ps}. &{} \end{array} \end{aligned}$$

(10)

Comparing these equilibrium quantities to those found in the case of private, profit-seeking companies, the only difference regards the indirect utilities, since now their sum corresponds to social welfare.⁵

3.2.2 Socially responsible production strategy

Consider now companies that adopt the socially responsible production strategy, therefore $(\omega ,\sigma )=(pub,sr)$. Each firm j maximizes the following objective function

$$\begin{aligned} o_{j}^{sr}=\left( a-\frac{y_{j}+\sum y_{-j}}{h}-c\right) y_{j}+z\left[ \left( y_{j}+\sum y_{-j}\right) \left( a-\frac{y_{j}+\sum y_{-j}}{2h} -c\right) +hL\right] . \end{aligned}$$

(11)

Appendix B provides a formal derivation of this functional form. Maximization with respect to $y_{j}$ yields

$$\begin{aligned} \frac{\partial o_{j}^{sr}}{\partial y_{j}}=a-c-\frac{2y_{j}+\sum y_{-j}}{h} +z\left( a-c-\frac{y_{j}+\sum y_{-j}}{h}\right) =0. \end{aligned}$$

In turn, the symmetric equilibrium is given by

$$\begin{aligned} y_{j}:=y_{pub}^{sr}=\frac{nh\left( a-c\right) \left( 1+z\right) }{n+1+nz} >0,\qquad j\in \left\{ 1, \ldots ,n\right\} , \end{aligned}$$

for $z<\frac{n+1}{n+2}$, where the subscript “ pub ” refers to the type of ownership, while the superscript “ sr” to the type of production strategy. Using the definition of $y_{j}$, the equilibrium price, profits, indirect utility, and welfare are:

$$\begin{aligned} \begin{array}{ll} p:=p_{pub}^{sr}=\frac{a+n\left( 1+z\right) c}{n+1+nz}\ge 0, &{} \\ \pi _{j}^{sr}:=\pi _{pub}^{sr}=n\frac{h\left( a-c\right) ^{2}\left( 1+z\right) }{\left( n+1+nz\right) ^{2}}\ge 0, &{} \quad j=1,\ldots ,n \\ V_{i}^{sr}:=V_{pub}^{sr}=\frac{n\left( a-c\right) ^{2}\left( 1+z\right) }{ 2\left( n+1+nz\right) ^{2}}\left( n+nz+2\right) +L\ge 0, &{} \quad i=1,\ldots ,h \\ W_{pub}^{sr}:=hV_{pub}^{sr}. &{} \end{array} \end{aligned}$$

(12)

Interestingly, there are no limitations on $z\in (0,1)$ for this market configuration. This implies that, unlike the oligopoly of privately-owned CSR firms, this market configuration can be implemented for any level of social concern.

3.2.3 Welfare comparison

We now compare the two production strategies in the setting of public companies. The results are summarized in the following proposition.

Proposition 2

Consider an oligopoly composed of public companies. For any $z \in (0,1)$, output, consumer surplus, and social welfare are higher, while profits and price are lower, in the case of CSR configuration compared to the case of profit-seeking configuration. That is,

$$\begin{aligned} y_{pub}^{ps}< y_{pub}^{sr}, \qquad p_{pub}^{ps}> p_{pub}^{sr}, \qquad V_{pub}^{ps}< V_{pub}^{sr}, \qquad \pi _{pub}^{ps} > \pi _{pub}^{sr}, \qquad W_{pub}^{ps}< W_{pub}^{sr}. \end{aligned}$$

Proof

The results immediately follow by comparing the equilibrium quantities in (10) with those in (12).□

The results in Proposition 2 are qualitatively similar to those in Proposition 1. Comparing the two ownership scenarios, however, there is a crucial difference. If the oligopoly is composed of privately-owned companies, there is no incentive to switch to a socially responsible production strategy, because, by doing so, the companies would lower their profits. If the oligopoly is composed of publicly-owned companies, instead, there is more than an incentive to switch to a socially responsible production strategy, since doing so is welfare-improving. In this case, the firms’ gain in terms of benefits more than compensates for the decrease in profits. This result is consistent with the substantial evidence showing that public companies tend to engage in socially responsible activities more often than private companies (Lee 2009; Lourenço and Branco 2013; Tagesson et al. 2009). For example, Lee (2009) compares the difference in CSR attitudes between public and private firms. The author empirically finds that publicly-owned companies have a more environmentally responsible behavior compared to privately-owned companies because the former are subjected to higher social pressure. Similar evidence is found in emerging countries (Lourenço and Branco 2013). Social pressure is also analyzed in the work of Tagesson et al. (2009), where the authors find that public corporations are more transparent and open to internet-based social disclosure. All together, these results are in line with those in Proposition 2 and offer a rationale for the suggestion that public companies are more willing to engage in CSR activities with respect to private companies, since social pressure become higher as social welfare decreases.

3.3 Private vs public CSR

We now investigate the equilibrium differences between a CSR oligopoly composed of private companies and one composed of public companies.

First, the comparison must be limited to the case $z<\frac{1}{n}$, otherwise firms belonging to an oligopoly of private CSR would get negative profits. In this case, it immediately follows that output is lower and prices are higher when CSR firms are publicly owned. It is also easy to see that profits are larger for publicly-owned CSR firms, given that $\text {sgn}(\pi _{pub}^{sr}-\pi _{pr}^{sr})=\text {sgn}(z\left( n+1\right) \left( n+nz-1\right) ^{2})>0$. The differences in terms of social welfare is

$$\begin{aligned} \text {sgn}(W_{pub}^{sr}-W_{pr}^{sr})=\text {sgn} \left[ n(z(n\left( 1+z\right) +1)-2)-2\right] <0, \end{aligned}$$

for $z<\frac{1}{n}$. Hence, the following result holds.

Theorem 1

Suppose $z\in \left( 0,\frac{1}{n}\right)$. Then, a CSR oligopoly of private companies is welfare enhancing compared to a CSR oligopoly of public companies. Overall, we have

$$\begin{aligned} y_{pr}^{sr}>y_{pub}^{sr}, \qquad p_{pr}^{sr}<p_{pub}^{sr}, \qquad \pi _{pr}^{sr}<\pi _{pub}^{sr}, \qquad W_{pr}^{sr}>W_{pub}^{sr}. \end{aligned}$$

Proof

The results immediately follow by comparing the equilibrium quantities in (9) with those in (12).□

The result in Theorem 1 can be explained as follows. In a public company, the socially responsible production strategy takes into account the fact that the company is owned by consumers. Therefore, the objective function is maximized by choosing an output level that trades off the opportunity cost of labor income (leisure) against dividend gain (profits). This is done by pricing leverage. Prices increase, and so do profits. But this comes at the expense of less output and, then, less welfare, compared to that obtained in a private company, also adopting a socially responsible production strategy.

3.4 Pareto optimum

We conclude our analysis on symmetric markets with the study of the conditions on the level of social concern that allow us to reach the Pareto Optimum for CSR firms of both ownership types. Consistent with the standard economic theory, the result replicates the case of perfect competition, with zero profits and no deadweight loss. We begin by deriving the level of utility determined by Pareto Optimal allocation.

Proposition 3

In the case of equal weights, i.e., for any $i,j\in \left\{ 1, \ldots ,h\right\}$, $\gamma _{i}=\gamma _{j}$, then the solution to maximization problem (33) is a Pareto Optimal allocation such that for any $i=1, \ldots ,h,$ $y_{i}=a-c,\ l_{i}=L-c\left( a-c\right)$ total utility is

$$\begin{aligned} hL+h\frac{1}{2}\left( a-c\right) ^{2}. \end{aligned}$$

Proof

In Appendix C.□

We then have the following result.

Proposition 4

Suppose firms are CSR.

• 1. In the case of private companies, then the total indirect utility is Pareto Optimal and profits are equal to zero if $z<\frac{1}{n}$.

• 2. In the case of public companies, then the total indirect utility is never Pareto Optimal for $z\in (0,1)$.

Proof

In Appendix D.□

4 Endogenous market structure

In this section we extend the baseline analysis by studying the presence of different types of firms in the industry. The coexistence of private and public companies requires an additional assumption on consumers. We assume that a number $h_{1}$ of consumers own a share of public companies (“ shareholders” ) and a number $h_{2}=h-h_1$ of consumers have no capital (“ propertyless” ). To be consistent with the baseline analysis, and to simplify the exposition, in what follows we set $h_{1}=h_{2}=\frac{h}{2}$.

We begin by considering the general case where the four types of firms coexist: private companies with (i) profit-seeking and (ii) CSR statute, and public companies with (iii) profit-seeking and (iv) CSR statute. We are interested in studying whether this industry configuration is stable.

4.1 Stability analysis

Consider an industry composed of $n_1$ public companies and $n_2$ private companies, with $n_1+n_2=n$. There are $m_{1}\le n_1$ public companies with a CSR statute, $n_{1}-m_{1}$ public companies with a profit-seeking statute $m_{2}\le n_2$ private companies with a CSR statute, and $n_{2}-m_{2}$ private companies with a profit-seeking statute.

The inverse demand function is

$$\begin{aligned} p=a-\frac{1}{h}\Big ( m_1y_{pub}^{sr}(m_1)+(n_1-m_1)y_{pub}^{ps}(n_1-m_1)+m_2y_{pr}^{sr}(m_2)+ (n_2-m_2)y_{pr}^{ps}(n_2-m_2) \Big ), \end{aligned}$$

where $y_{\omega }^{\sigma }(m)$ are the possible firms’ outputs, depending on the ownership structure $\omega \in \{pr,pub\}$, the production strategy $\sigma \in \{ps,sr\}$, and the number $m\in \{m_1,n_1-m_1,m_2,n_2-m_2\}$ of firms of the same type. For each type of firm, the objective functions are as in the baseline model, but now all four types of firms coexist in the same industry.

Firms of each type maximize their profits simultaneously. By computing the first order conditions (see Appendix E), then invoking symmetry, we get

$$\begin{aligned} \begin{aligned} y_{pub}^{sr}(m_{1})&=\dfrac{h(1+z)(a-c)\left( 1-zm_{2}\right) }{z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1}, \\ y_{pub}^{ps}(n_{1}-m_{1})&=\dfrac{h(a-c)\left( 1-zm_{2}\right) }{z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1}, \\ y_{pr}^{sr}(m_{2})&=\dfrac{h(a-c)(z(m_{1}z-m_{2}+n_{1}+n_{2})+1)}{z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1}, \\ y_{pr}^{ps}(n_{2}-m_{2})&=\dfrac{h(a-c)\left( 1-zm_{2}\right) }{z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1}. \end{aligned} \end{aligned}$$

(13)

Restricting the level of social concern to $z< \frac{1}{m_{2}}$ ensures the positivity of the equilibrium outputs. Letting $\pi _{\omega }^{\sigma }(m)$ denote the equilibrium profits of each of the m firms of type $(\omega ,\sigma )$, with $m\in \{m_1,n_1-m_1,m_2,n_2-m_2\}$, we have

$$\begin{aligned} \begin{aligned} \pi _{pub}^{sr}(m_{1})&=\dfrac{h(1+z)(a-c)^{2}(1-m_{2}z)^{2}}{\left[ z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1\right] ^{2}}, \\ \pi _{pub}^{ps}(n_{1}-m_{1})&=\dfrac{h(a-c)^{2}(m_{2}z-1)^{2}}{\left[ z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1\right] ^{2}}, \\ \pi _{pr}^{sr}(m_{2})&=\dfrac{h(a-c)^{2}(1-m_{2}z)\left[ z(m_{1}z-m_{2}+n_{1}+n_{2})+1\right] }{\left[ z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1\right] ^{2}}, \\ \pi _{pr}^{ps}(n_{2}-m_{2})&=\dfrac{h(a-c)^{2}(1-m_{2}z)^{2}}{\left[ z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1\right] ^{2}}. \end{aligned} \end{aligned}$$

(14)

Next, we verify the stability of the market partition using the coalition theory approach, as in D’Aspremont et al. (1983), Donsimoni (1985) and Donsimoni et al. (1985).

Notice that we will evaluate stability among CSR and profit seeking firms both of private and public ownership. Instead, we will not evaluate stability among private and public companies because, while a firm’s statute can be considered a choice variable, the firms’ ownership is taken as given, i.e., it cannot be changed due to firms’ incentives. This is so because the choice between owning or selling a firm, for an entrepreneur, depends on factors that are not analyzed in the present framework, such as, the company value.

A partition $\left\{ m_{1},n_{1}-m_{1}\right\}$ of public companies is stable if (i) no CSR public company desires to become profit-seeking ( internal stability 1) (ii) no profit-seeking public company desires to shift to CSR (external stability 1). The same conditions apply for a partition $\left\{ m_{2},n_{2}-m_{2}\right\}$ of private companies. Finally, note that the production strategy is chosen based on the profits obtained, for a given objective function.

Consider first the public companies and the internal stability criterion. The CSR coalition of size $m_{1}$ is stable if none of its members has an incentive to deviate unilaterally and join the profit-seeking coalition, which is initially of size $n_1-m_1$. Let

$$\begin{aligned} \pi _{pub}^{ps}(n_{1}-m_{1}+1)=\frac{h(a-c)^{2}(1- {m_{2}}z)^{2}}{\left[ z({m_{1}}-{m_{2}}-1)+{n_{1}}+{n_{2}}+1\right] ^{2}}, \end{aligned}$$

(15)

denote the profits of a profit-seeking firm, when a single CSR public company leaves the CSR coalition to become profit-seeking, thereby increasing the size of the profit-seeking coalition by one unit.

Similarly, the profits of a CSR firm when a profit-seeking firm changes its production strategy becoming a CSR firm and, therefore, increasing the size of the CSR coalition by one unit are:

$$\begin{aligned} \pi _{pub}^{sr}(m_{1}+1)=\frac{h(a-c)^{2}(1+z)(1-{m_{2}}z)^{2}}{\left[ \left( {m_{1}}-{m_{2}}\right) z+{n_{1}}+{n_{2}} +z+1\right] ^{2}}. \end{aligned}$$

(16)

Hence the stability conditions for a market structure with $m_{1}$ CSR and $n_{1}-m_{1}$ profit-seeking public companies are:

$$\begin{aligned} \left\{ \begin{array}{c} \pi _{pub}^{sr}(m_{1})\ge \pi _{pub}^{ps}(n_{1}-m_{1}+1)\text { { (internal stability)}} \\ \pi _{pub}^{ps}(n_{1}-m_{1})\ge \pi _{pub}^{sr}(m_{1}+1) \text { {(external stability).}} \end{array} \right. \end{aligned}$$

(17)

The CSR coalition of size $m_1\ge 1$ is internally stable if and only if the profits of each single CSR firm of this coalition are higher than those that the same firm would attain by moving from the CSR coalition towards the alternative profit-seeking coalition. Conversely, a coalition of $m_{1}$ CSR firms is externally stable if and only if, for $m_{1}\le n_{1}-1$, there is no incentive for a firm in isolation to move from the profit-seeking coalition towards the CSR one.

The following proposition applies.

Proposition 5

An industry configuration of public companies composed of a coalition of CSR firms and a coalition of profit seeking firms is unstable. The unique stable configuration is the CSR grand coalition.

Proof

In Appendix F.□

Proposition 5 shows that an industry configuration of public companies composed of both CSR and profit-seeking firms is unstable. A possible way to overcome this result could be the implementation of fixed costs in the CSR technology. We will return to this point in Appendix H.

Consider next the stability of the group of private companies.

Proposition 6

Consider an industry configuration of private companies composed of a coalition of $m_2$ CSR firms and a coalition of $n_2-m_2$ profit-seeking firms. Then, there exist $m_{2}^{I}$ and $m_{2}^{E}$ , with $m_{2}^{E}-m_{2}^{I}=1$ such that if $m_{2}\in \left[ m_{2}^{I},m_{2}^{E}\right]$, the industry configuration is stable.

Proof

In Appendix F.□

Proposition 6 shows that, albeit a stable industry configuration of private profit-seeking and private CSR firms may exist, the conditions of stability are indeed quite narrow, since only one value of $m_{2}$ admits stability. Therefore this industry configuration is not stable, in general. By contrast, Proposition 6 implies that configurations composed by symmetric private companies (either CSR or profit seeking) are more likely to be stable. In the light of the results of Proposition 5 and 6, in the next sections we study the two mixed configurations that seem more stable, namely, an industry of public companies that adopt a CSR statute alternatively with private companies that adopt either a profit-seeking or CSR statute.⁶

4.2 Public CSR and private profit seeking

We now analyze the first of the two stable mixed-market configurations. Assume that the industry is partitioned into two groups: $n_1$ public CSR companies and $n_2$ private profit-seeking companies, with $n_1+n_2=n$. We will begin by obtaining the equilibrium profits in the case where the CSR commitment z may be set by the government to maximize welfare. We will then evaluate whether the case in which the CSR commitment may be chosen by the public companies.

4.2.1 Government choice of CSR commitment

In this section, we assume that a government is present in the economy, and it is entitled to set the companies’ CSR effort with the aim to maximize social welfare. This case has relevant implications, since implementing CSR governmental guidelines might be necessary in an industry with CSR firms, as shown by Xu and Lee (2019) in an industry where a privatization policy is applied. In addition, Kim et al. (2019) show that the level of CSR effort influences the validity of privatization policies. Moreover, assuming that the government may intervene in the CSR level of private and public companies is also empirically relevant, given the introduction of public policies on CSR in Europe (Steurer 2010), U.K., U.S. and many developing countries all over the world (Xu and Lee 2019). Finally, notice that this case encompasses a “ second best” result because the government is not in charge of establishing the equilibrium price and quantity.

Consider first the market equilibrium. Profit maximization with respect to quantities yields

$$\begin{aligned} y_{pub}^{sr}(n_1)=\frac{h\left( 1+z\right) (a-c)}{n_{1}\left( 1+z\right) +n_{2}+1},\\ y_{pr}^{ps}(n_2)=\frac{h(a-c)}{n_{1}\left( 1+z\right) +n_{2}+1}. \end{aligned}$$

In turn, equilibrium profits are

$$\begin{aligned} \pi _{pub}^{sr}(n_1)=\frac{h(z+1)(a-c)^{2}}{\left[ {n_{1}}\left( 1+z\right) +n_{2}+1\right] ^{2}},\\ \pi _{pr}^{ps}(n_2)=\frac{h(a-c)^{2}}{\left[ {n_{1}}\left( 1+z\right) + {n_{2}}+1\right] ^{2}}. \end{aligned}$$

It is immediate to verify that $\pi _{pub}^{sr}(n_1) - \pi _{pr}^{ps}(n_2)>0$ for each $n_1$ and $n_2=n-n_1$. Therefore CSR public companies are more profitable than profit-seeking private companies. As stressed above, we do not analyze the choice of ownership, because the elements necessary to determine the ownership incentives (e.g., value of the firm, alternative investments, etc.) are not part of the present framework, and such an investigation is, anyway, out of the scope of this paper.

We now assume that there is a pre-stage in which the government sets the level of the CSR effort with the aim to maximize social welfare. Recall that we have assumed that $h_1=\frac{h}{2}$ consumers are shareholders and $h_2= \frac{h}{2}$ are propertyless. Let $W_1$ be the level of welfare of consumers who are shareholders, $W_2$ be the level of welfare of consumers who are propertyless, and $W_3$ be the level of welfare of the $n_{2}$ private firms (entrepreneurs). In this industry configuration, the welfare function is given by

$$\begin{aligned} W =W_{1}+W_{2}+W_{3}, \end{aligned}$$

(18)

where

$$\begin{aligned} W_1&= n_1\left[ \Big (n_1y_{pub}^{sr}(n_1) +n_2 y_{pr}^{ps}(n_2)\Big ) \left( a-c-\dfrac{n_1y_{pub}^{sr}(n_1) +n_2 y_{pr}^{ps}(n_2)}{h}\right) + \dfrac{h}{2}L \right] , \\ W_2&= n_2\left[ \dfrac{h}{2}L +h \left( \dfrac{n_1y_{pub}^{sr}(n_1) +n_2 y_{pr}^{ps}(n_2)}{h} \right) ^2 \right] , \\ W_3&=n_2\pi _{pr}^{ps}(n_2). \end{aligned}$$

In expression (18), we have decomposed the level of total welfare into the sum of the levels of welfare of each type of agents. We can also interpret (18) as the sum of the levels of wealth of three distinct types of agents, each with a different level of wealth: the propertyless consumers are the poorest, the shareholders are middle class, and the entrepreneurs represent the rich class.⁷

The solution of the welfare maximization is subgame perfect Nash equilibrium, which we solve by backward induction. Substituting the equilibrium values of $y_{pub}^{sr}(n_1)$ and $y_{pr}^{ps}(n_2)$, we can rewrite (18) as

$$\begin{aligned} W=h(a-c)^{2}\dfrac{ n_{1}^{2}(1+z)[n_2(1+z)+1]+n_1n_2[2n_2(z+1)+1] +n_2^3 +n_2}{[n_1(1+z)+n_2+1]^2}+hL(n_1+n_2). \end{aligned}$$

(19)

The following result holds.

Proposition 7

Suppose the government chooses the level of effort in CSR activities. For $n_{1}>\frac{n_{2}-1}{2}$, it chooses the maximum level possible, $z=z^{w1}:=1$. For $n_{1}<\frac{n_{2}-1}{2}$, it chooses the minimum level possible, $z=z^{w2}:=0$.

Proof

In Appendix I.□

If the number of CSR public companies is sufficiently larger than the number of profit-seeking private companies, then the CSR effort is welfare enhancing. The results of Proposition 7 may be explained by analyzing the effects of CSR effort over each social group, namely, shareholders, propertyless and entrepreneurs. Differentiating each component of welfare we have

$$\begin{aligned} \frac{\partial W_{1}}{\partial z }&=-\frac{hn_{1}(a-c)^{2}[n_{1} ( 1+z ) +n_{2}-1] }{ [ n_{1} ( 1+z ) +n_{2}+1 ]^{3}}<0, \\ \frac{\partial W_{2}}{\partial z }&=\frac{2hn_{1}(a-c)^{2}[n_{1} ( 1+z ) +n_{2}] }{ [ n_{1} ( 1+z ) +n_{2}+1 ]^{3}}>0, \\ \frac{\partial W_{3}}{\partial z }&=-\frac{2hn_{1}n_2(a-c)^{2} }{ [ n_{1} ( 1+z ) +n_{2}+1 ]^{3}}<0. \end{aligned}$$

The welfare of both shareholders and entrepreneurs decreases with an increase in z, while the welfare of propertyless increases. Therefore,

Corollary 2

CSR activities increase the welfare of propertyless and decreases the welfare of shareholders and entrepreneurs.

Interestingly, CSR activities exhibit redistributive effects. This result can be explained by noticing that an increase in z increases competition, and thus lowers the output prices. Those who gain from it are the propertyless because, unlike shareholders, their gain is not counterbalanced by the loss in terms of profits. Corollary 2 thus helps providing an intuition for Proposition 7. The gain of the propertyless counterbalances the losses of shareholders and private firms when the presence of CSR activities, represented by the number of CSR companies, is sufficiently large. In particular, notice that

$$\begin{aligned} \frac{\partial W_{2}}{\partial z }-\left( \left| \frac{\partial W_{1}}{\partial z }\right| +\left| \frac{\partial W_{3}}{\partial z } \right| \right) =\frac{hn_{1}(a-c)^{2}[n_{1} ( 1+z ) +n_{2}-1] }{ [ n_{1} ( 1+z ) +n_{2}+1 ]^{3}}>0, \end{aligned}$$

for $n_{1}>\frac{n_{2}-1}{1+z}$. When the share of entrepreneurs is large ($n_1$ ), the positive marginal effect of CSR effort on propertyless is stronger than the sum of negative marginal effects for shareholders and entrepreneurs.

4.2.2 Private choice of CSR commitment

Consider next the case in which CSR companies may choose their level of effort in CSR activities, z. To do so, suppose that there is a pre-stage where each CSR company j sets its level of CSR commitment, $z_{j}$. Again, the solution of this problem is subgame perfect Nash equilibrium by backward induction. Quantity competition in the market stage yields the following equilibrium quantities:

$$\begin{aligned} y_{pub}^{sr}(z_{j},z_{-j};n_{1})&=\frac{h(z_{j}+1)(a-c)}{ (n_{1}-1)z_{-j}+n_{1}+n_{2}+z_{j}+1},\qquad j=1,\ldots ,n_{1}, \\ y_{pr}^{ps}(z_{j},z_{-j};n_{2})&=\frac{h(a-c)}{ (n_{1}-1)z_{-j}+n_{1}+n_{2}+z_{j}+1},\qquad j=1,\ldots .n_{2}. \end{aligned}$$

Proposition 8

Suppose the CSR companies may choose the level of effort in CSR activities. Then they choose the maximum level possible, $z=1$.

Proof

In Appendix J.□

The first step to clarify the intuition of Proposition 8 is to examine the effects of CSR effort on the social welfare of shareholders, namely, $W_1$. We get

$$\begin{aligned} \frac{\partial W_{1}}{\partial z }&=-\frac{ hn_{1}^{2}(a-c)^{2}(n_{1}z+n_{1}+n_{2}-1)}{(n_{1}z+n_{1}+n_{2}+1)^{3}}<0. \end{aligned}$$

The CSR effort is in the hands of CSR companies, and they exert it as much as possible, even if it harms shareholders’ welfare. This counterintuitive result may be explained by noticing that the CSR objective function aims at the maximization of consumers surplus of all consumers. Considering the social welfare of the group of propertyless, we have

$$\begin{aligned} \frac{\partial W_{2}}{\partial z }&=\frac{ 2hn_{1}n_{2}(a-c)^{2}(n_{1}z+n_{1}+n_{2})}{(n_{1}z+n_{1}+n_{2}+1)^{3}}>0. \\ \end{aligned}$$

Conversely, shareholders are both consumers and firm owners, thus they face a trade-off: the higher the welfare share due to consumption, the lower the welfare share due to profits.

The results in Proposition 7, Corollary 2 and Proposition 8 have some straightforward policy implications. For an utilitarian government, the choice between the highest level of CSR effort or preventing any form of CSR depends on the composition of the industry. By contrast, a redistributive government would raise the level of CSR effort as much as possible. The independent choice of CSR effort is aligned with a redistributive government or an utilitarian government when the industry is composed of a sufficiently large number of public CSR companies. In this case, self regulation works. When a government is utilitarian and the industry is mainly composed of private companies, the independent choice of CSR effort is not in line with the social incentive, and a government intervention may be desirable.

4.3 Public CSR and private CSR

We now focus on the second stable mixed-market configuration. Assume that the industry is partitioned into two groups: $n_1$ public CSR companies and $n_2$ private CSR companies, with $n_1+n_2=n$. In this case, the level of CSR effort may change according to the type of ownership of the company. Let $z_{1}$ and $z_2$ be the level of CSR commitment of public and private companies, respectively. Similarly to the previous case, we first obtain the equilibrium profits in the case where the CSR commitments may be set by the government to maximize welfare. We then evaluate the case in which the CSR commitment may be chosen by each company type, according to its ownership.

We begin by considering the market equilibrium in the second stage when CSR efforts are exogenous. Market equilibrium yields

$$\begin{aligned} y_{pub}^{sr}(n_1)&=\frac{h(1+z_{1})(a-c)\left( 1-n_2z_{2}\right) }{n_1\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1}>0, \qquad \text {if } z_{2}< \widehat{z}_{2}=\frac{1}{n_{2}}, \\ y_{pr}^{sr}(n_2)&=\frac{h(a-c)\left( 1+z_{1}\right) }{n_1\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1}. \end{aligned}$$

In turn, equilibrium profits are

$$\begin{aligned} \pi _{pub}^{sr}(n_1)&=\frac{h(1+z_{1})(a-c)^{2}\left( 1-n_{2}z_{2}\right) ^{2}}{\left[ n_1\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{2}}, \\ \pi _{pr}^{sr}(n_2)&=\frac{h(a-c)^{2}\left[ n_1z_{2}(1+z_{1})+1\right] \left( 1-n_2z_{2}\right) }{\left[ n_1\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{2}}. \end{aligned}$$

Notice that both equilibrium profits are positive if $z_{2}<\widehat{z}_{2}$ . Also, this condition ensures that this mixed market configuration indeed exists. We thus define the upper bound of the possible CSR effort for private companies such that this industry configuration exists as $\bar{z_{2} }\in (0,\widehat{z}_{2})$.

Comparing the two equilibrium profits, we get

$$\begin{aligned} \pi _{pub}^{sr}(n_1)-\pi _{pr}^{sr}(n_2) >0 \qquad \text {if } z_2<\tilde{z} _2 :=\dfrac{z_1}{(1+z_1)(n_1+n_2)}, \end{aligned}$$

where $\widetilde{z}_{2}<\widehat{z}_{2}$. Therefore, the profits of a CSR public company are higher than those of a CSR private company only if the CSR commitment of the private company is sufficiently low.

4.3.1 Comparison with the symmetric case

The present framework allows to determine whether the welfare outcomes of publicly and privately owned CSRs are consistent with what happens in the symmetric case. In particular, in Section 3.3 we have evaluated the equilibrium differences between a CSR oligopoly composed of private companies and one composed of public companies. Theorem 1 had shown that the private-company oligopoly is welfare enhancing compared to the public-company oligopoly.

To verify whether the findings of Theorem 1 are robust to the asymmetric case, we compare the welfare of shareholders consumers ($W_{1}$) with the sum of welfare of propertyless consumer ($W_{2}$) and of profit seeking firms ($W_{3}$). Indeed, while $W_{1}$ amounts to the welfare of the “ public side” of the economy, $W_{2}+W_{3}$ corresponds to the welfare of the “ private side” of the economy. The fact that the size of each population is normalized to $\frac{h}{2}$ allows the comparison. The welfare results described in the proposition below are consistent to those in Theorem 1.

Proposition 9

Suppose a setting where public and private CSR companies coexist. Then the social welfare of the private side of the economy is larger than that of the public side of the economy.

Proof

In Appendix K.□

4.3.2 Government choice of CSR commitment

Consider next the case in which the government sets the level of the CSR effort with the aim to maximize social welfare. The welfare function is now represented by $W(z_1,z_2)$, with the same functional form as in the previous configuration. However, now the government must choose two different levels of CSR effort, one for each type.

Substituting the equilibrium values of $y_{pub}^{sr}(n_1)$ and $y_{pr}^{sr}(n_2)$, we may rewrite (18) as

$$\begin{aligned} {\small W(z_1,z_2) =h\frac{(a-c)^{2}\left[ {n_{1}}^{2}({z_{1}} +1)^{2}-{n_{1}}(1+{z_{1}})\left( {n_{2}^{2}z_{2}^{2}}-2 {n_{2}}-1\right) +{n_{2}}({n_{2}}+2-2{n_{2}z_{2}} )\right] }{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{2}}+hL.} \end{aligned}$$

The first order condition of W with respect to $z_2$ yields

$$\begin{aligned} \frac{\partial W\left( y_{i}^{sr},y_{d}^{ps}\right) }{\partial z_{2}}=\frac{ 2hn_{2}(a-c)^{2}\left[ n_{1}\left( 1+z_{1}\right) +1\right] \left[ n_{1}\left( 1+z_{1}\right) +n_{2}\right] (1-n_{2}z_{2})}{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{3}}=0, \end{aligned}$$

for $z_2=\widehat{z}_{2}$. Hence, the optimal CSR effort of private companies chosen by the government is the highest level of effort that admits positive profits and output, $z_2^{w}=\bar{z_{2}}$. This is natural, considering the second-best nature of the government intervention. Also, it is independent on the government choice about the CSR effort of public companies. Hence, setting $z_2$ as high as possible has unambiguously positive effect on social welfare.

Conversely the first order condition of W with respect to $z_1$ gives

$$\begin{aligned} \frac{\partial W\left( y_{i}^{sr},y_{d}^{ps}\right) }{\partial z_{1}}=\frac{ hn_{1}(a-c)^{2}(1-{n_{2}z_{2}})^{2}\left[ n_{1}(1+z_{1})-n_{2}(1-z_{2})+1\right] }{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{3}}=0, \end{aligned}$$

which, substituting $z_{2}=z_2^{w}$, holds for

$$\begin{aligned} z_{1}=\frac{n_{2} (1-\bar{z_{2}})-n_{1}-1}{n_{1}}, \end{aligned}$$

whose sign is ambiguous. The result can be summarized in the next proposition. For convenience, define

$$\begin{aligned} \widehat{n}_{1}:=\frac{1}{4}\left[ \left( 8n_{2}^{2}(1-\overline{z} _{2})^{2}+1\right) ^{\frac{1}{2}}-3\right] . \end{aligned}$$

Proposition 10

Suppose the government chooses the level of effort in CSR activities. It sets $z_{2}^{w}=\bar{z_{2}}$. For

• $n_{1}>\widehat{n}_{1}$, it chooses the maximum level possible, $z^{w}_{1}=1$;

• $n_{1}<\widehat{n}_{1}$, it chooses the minimum level possible, $z^{w}_{1}=0$.

Proof

In Appendix L.□

For what concern the CSR effort of public companies, the results in Proposition 10 are qualitatively similar to those in Proposition 7: the CSR effort of public companies is welfare improving only if the number of CSR public companies is sufficiently larger than the number of profit-seeking companies. By contrast, the government sets the highest CSR commitment admissible for private companies. As in the previous case, the effects of CSR effort in each social group shed light on the mechanisms behind the result.

Corollary 3

CSR activities of public companies increase the welfare of propertyless and decreases the welfare of shareholders and private companies. The CSR activities of private companies increase the welfare of propertyless and decreases the welfare of shareholders. The effect on the profits of private companies is positive for $n_{1}>\frac{1-n_{2}(1+z_{2})}{ (1+z_{1})(2n_{2}z_{2}-1)}$ and negative for $n_{1}<\frac{1-n_{2}(1+z_{2})}{ (1+z_{1})(2n_{2}z_{2}-1)}$.

Proof

In Appendix M.□

Again, the effects on each social group are similar as in the previous case, with similar intuition: the welfare of consumers-shareholders decreases with $z_{1}$ and $z_{2}$, while the welfare of consumers-propertyless increase. The only exception, is the effect of $z_{2}$ on private profits: it has a negative effect only if the number of public companies is sufficiently small.

4.3.3 Private choice of CSR commitment

We consider now the case in which each CSR company chooses its effort in CSR activities based on its ownership. Market competition yields the following quantities:

$$\begin{aligned}&y_{j}^{sr}\left( z_{j},z_{-j},z_{b},z_{-b}\right) =\frac{h(a-c)(1+{z_{j}})\left( 4-z_{b}-\sum z_{-b}\right) }{4({n_{1}}+{n_{2}} +1)+4\left( z_{j}+\sum z_{-j}\right) -\left( z_{b}+\sum z_{-b}\right) },\\&y_{b}^{sr}\left( z_{j},z_{-j},z_{b},z_{-b}\right) =\frac{h(a-c)\left[ 4+ {z_{b}}\left( n_{1}+n_{2}-1+\sum z_{-j}\right) -\sum z_{-b}\right] }{ 4({n_{1}}+{n_{2}}+1)+4\left( z_{j}+\sum z_{-j}\right) -\left( z_{b}+\sum z_{-b}\right) }. \end{aligned}$$

with $j\in \left\{ 1, \ldots ,n_{1}\right\}$ being public companies and $b\in \left\{ 1, \ldots ,n_{2}\right\}$ being private ones. Following the previous procedure, we differentiate $o_{ j}^{sr}\left( z_{j},z_{-j},z_{b},z_{-b}\right)$ and $o_{b}^{sr} \left( z_{j},z_{-j},z_{b},z_{-b}\right)$ with respect to $z_{j}$ and $z_{b}$ , respectively, and invoke symmetry, $z_{j}=z_{-j}$ and $z_{b}=z _{-b}$.

We get

$$\begin{aligned}&\frac{\partial o_{j}^{sr}(z_{1},z_{2};n_{1},n_{2})}{\partial z_{1}}= \\&h\frac{(a-c)^{2}\left[ \begin{array}{c} 32n_{1}^{3}\left( 1+z_{1}\right) ^{3}+24n_{1}^{2}(1+z_{1})^{2}\left[ n_{2}(4-z_{2})+4\right] + \\ 8n_{1}(z_{1}+1)\left[ n_{2}^{2}\left[ 12-z_{2}\left( 6-z_{2}\right) \right] +8n_{2}(3-z_{2})+16\right] + \\ n_{2}\left[ n_{2}^{2}(-(z_{2}-4))((z_{2}-4)z_{2}+8)+4n_{2}\left[ 24-z_{2}(16+z_{1}z_{2}-z_{2})\right] +16(2z_{1}z_{2}+z_{2}+8)\right] \\ -64\left( 1+z_{1}\right) \end{array} \right] }{\left[ 4(n_{1}z_{1}+n_{1}+n_{2}+1)-n_{2}z_{2}\right] ^{3}}+hL>0\nonumber \end{aligned}$$

(20)

and

$$\begin{aligned}&\frac{\partial o_{b}^{sr}(z_{1},z_{2};n_{1},n_{2})}{\partial z_{1}}=\\&h\frac{(a-c)^{2}(n_{1}z_{1}+n_{1}+n_{2})\left[ \begin{array}{c} 16\left[ 2n_{1}^{2}(z_{1}+1)^{2}+n_{1}(4n_{2}+3)(1+z_{1})+2n_{2}^{2}\right] \\ +(n_{2}-1)n_{2}z_{2}^{2}+4\left( 12n_{2}+z_{2}-4\right) \\ -12z_{2}(n_{2}-1)(n_{1}z_{1}+n_{1}+n_{2}) \end{array} \right] }{(4(n_{1}z_{1}+n_{1}+n_{2}+1)-n_{2}z_{2})^{3}}+hL>0.\nonumber \end{aligned}$$

(21)

Both public and private companies set the level of CSR as high as they can, with similar intuition as in Proposition 8. In addition, notice that equations (20) and () are positive irrespective of the behavior of the other CSR type. Hence CSR effort does not entail any strategic interaction among companies of different ownership. The results can thus be summarized as follows:

Proposition 11

Suppose the CSR public and private companies may choose the level of effort in CSR activities. Then they choose the maximum level possible, $z_{1}=1,z_{2}=\bar{z}_{2}=\frac{1}{2(n_{1}+n_{2})}$.

The results in Proposition 10 and 11 have policy implications that are qualitatively similar to those discussed at the end of Sect. 4.2.2.

5 Concluding remarks

We have studied the effects of CSR on consumers’ welfare when the industry is either privately or publicly owned. In line with the empirical evidence, consumers’ ownership gives an incentive to adopt a socially responsible, welfare improving statute. Our results support a market structure of CSR public companies if the level of CSR engaged by the firms is medium-high, and a market structure of CSR private companies if the level of CSR is low. In the latter case, we show that social welfare enhances compared to the cases of both a publicly-owned CSR and profit seeking oligopoly. The analysis is then extended to consider the strategic interplay among different firm types in asymmetric markets.

Our results suggest that policies promoting CSR activities are generally welfare enhancing. In case of symmetric markets, CSR production strategy is beneficial for social welfare, regardless of the type of industry ownership. When the market configuration is mixed, the government always supports the highest admissible CSR effort for private companies. By contrast, the CSR effort of public companies is socially optimal only when they have a large share of the market, otherwise, the government might prevent them to adopt any CSR production strategy at all. Moreover, our results support self regulation whenever the share of public companies is sufficiently large, since companies independently choose the socially optimal level of CSR effort, and private and public incentives are aligned.

On the management side, developing CSR strategies by the company itself might prevent more severe government regulations that might have detrimental effects on production, since these regulations would increase economic costs and limit the flexibility of managerial decision (Mullerat 2010; Ksiȩżak 2016).

Appendices

Appendices

1.1 Appendix A: consumer’s problem

In what follows, we focus on the “ public company” case where consumers own a share $\alpha _{ij}$ of firms. The result for private companies is the same by setting $\alpha _{ij}=0$. In any case, the good’s demand is the same in both cases, what changes is the leisure choice.

Consumer i’s maximization problem is as follows: for given $a,p^\sigma _{pub},L\in \mathbb {R}_{++}$,$\ \left( \alpha _{ij}\right) _{j=1}^{n}\in \Delta ^{n-1}:=\left\{ \alpha _i \in \mathbb {R} _{+}^{n}:\sum _{j=1}^{n} \alpha _{ij}=1\right\}$ and $\left( \pi ^\sigma _{j}\right) _{j=1}^{n}\in \mathbb {R}_{+}^{n}$,

$$\begin{aligned} \begin{array}{lllll} &{} \max _{\left( y_{i},l_{i}\right) }\ ay_{i}-\frac{1}{2}y_{i}^{2}+l_{i} &{} &{} &{} \\ \text {s.t.} &{} -p^\sigma _{pub}y_{i}-l_{i}+\left( L+\sum \nolimits _{j=1}^{n}\alpha _{ij}\pi _{j}^{\sigma }\right) \ge 0, &{} &{} \lambda _{i} &{} \\ &{} y_{i}\ge 0, &{} &{} \mu _{i} &{} \\ &{} l_{i}\ge 0 , &{} &{} \eta _{0i} &{} \\ &{} L-l_{i}\ge 0, &{} &{} \eta _{1i} &{} \end{array} \end{aligned}$$

(22)

The following result holds.

Proposition 12

If $\ \Pi _{pub,i}^{\sigma }<p^\sigma _{pub}a$, $a>p^\sigma _{pub}$ and $\Pi _{pub,i}^{\sigma }<p^\sigma _{pub}\left( a-p^\sigma _{pub}\right) <\Pi _{pub,i}^{\sigma } +L$, then Problem (22) has the unique solution $\left( y_{i},l_{i}\right) =\left( a-p^\sigma _{pub},\ \left( L+\Pi _{pub,i}^{\sigma }\right) -p^\sigma _{pub}\left( a-p^\sigma _{pub}\right) \right)$.

Proof

We have that a solution to the maximization problem exists and it is characterized by the following Kuhn-Tucker conditions:

$$\begin{aligned} D_{y_{i}}\mathcal {L}=0: \qquad&a-y_{i}-\lambda _{i}p^\sigma _{pub}+\mu _{i} =0 \end{aligned}$$

(23)

$$\begin{aligned} D_{l_{i}}\mathcal {L}=0 \qquad&1-\lambda _{i}+\eta _{0i}-\eta _{1i} =0 \end{aligned}$$

(24)

$$\begin{aligned}&\min \left\{ -p^\sigma _{pub}y_{i}-l_{i}+\left( L+ \Pi _{pub,i}^{\sigma }\right) ,\lambda _{i}\right\} =0 \end{aligned}$$

(25)

$$\begin{aligned}&\min \left\{ y_{i},\mu _{i}\right\} =0 \end{aligned}$$

(26)

$$\begin{aligned}&\min \left\{ l_{i},\eta _{0i}\right\} =0 \end{aligned}$$

(27)

$$\begin{aligned}&\min \left\{ L-l_{i},\eta _{1i}\right\} =0 \end{aligned}$$

(28)

Notice that

• 1. At least one of the two multipliers $\eta _{0i},\eta _{1i}$ has to be zero if:

  • (a) $l_{i}=0$, then $\eta _{0i}\ge 0$ and $\eta _{1i}=0;$

  • (b) $l_{i}\in \left( 0,L\right)$, then $\eta _{0i}=0$ and $\eta _{1i}=0;$

  • (c) $l_{i}=L$, then $\eta _{0i}=0$ and $\eta _{1i}\ge 0.$

• 2. $y_{i}\le a$. Suppose otherwise, i.e., $y_{i}>a>0$; then from (26), we have $\mu _{i}=0$ and from (23), we get $0\le \lambda _{i}p^\sigma _{pub}=a-y_{i}<0$, a contradiction.

• 3. $-p^\sigma _{pub}y_{i}-l_{i}+\left( L+ \Pi _{pub,i}^{\sigma } \right) =0$ because by assumption, $\Pi _{pub,i}^{\sigma } <p^\sigma _{pub}a$, and then $\lambda _{i}>0$. Suppose otherwise, i.e., $\lambda _i =0$. We then consider the three cases of point 1. above.

  • (a) Then, equation (24) becomes $0=1-\lambda _{i}+\eta _{0i}-\eta _{1i}=1+\eta _{0i}$ and then $\eta _{0i}=-1$, contradicting (27)

  • (b) Then, equation (24) becomes $0=1$, a contradiction.

  • (c) Then, conditions (23)-(28) become

    $$\begin{aligned} a-y_{i}+\mu _{i}&=0 \end{aligned}$$

    (29)
    $$\begin{aligned} 1-\eta _{1i}&=0 \end{aligned}$$

    (30)
    $$\begin{aligned} -p^\sigma _{pub}y_{i}+\Pi _{pub,i}^\sigma&\ge 0 \end{aligned}$$

    (31)
    $$\begin{aligned} \min \left\{ y_{i},\mu _{i}\right\}&=0 \end{aligned}$$

    (32)

  Now, if $y_{i}>0$, then $\mu _{i}=0$ and from (29), we have $y_{i}=a$ and from (31), we get $-p^\sigma _{pub}y_{i}+\Pi _{pub,i}^\sigma \ge 0$ or $\Pi _{pub,i}^\sigma \ge p^\sigma _{pub}a$, contradicting the assumption that $\Pi _{pub,i}^\sigma < p^\sigma _{pub}a$. If $y_{i}=0$, then from (29) above, we do have $\mu _{i}=-a<0$, contradicting (32). Let’s now see under which conditions $y_{i}>0$ and $l_{i}\in \left( 0,L\right)$. From the analysis above, conditions (29)-(32) become

  $$\begin{aligned} \begin{array}{lllll} a-y_{i}-\lambda _{i} p^\sigma _{pub} &{} &{} =0 &{} &{} \\ 1-\lambda _{i} &{} &{} =0 &{} &{} \\ - p^\sigma _{pub}y_{i}-l_{i}+\left( L+\Pi _{pub,i}^\sigma \right) &{} &{} =0 &{} &{} \\ \mu _{i} &{} &{} =0 &{} &{} \\ \eta _{0i} &{} &{} =0 &{} &{} \\ \eta _{1i} &{} &{} =0 &{} &{} \end{array} \end{aligned}$$

  and then $\lambda _{i}=1$, and

  $$\begin{aligned} \begin{array}{lll} y_{i} &{} = &{} a- p^\sigma _{pub}, \\ l_{i} &{} = &{} \left( L+\Pi _{pub,i}^\sigma \right) - p^\sigma _{pub}\left( a- p^\sigma _{pub}\right) . \end{array} \end{aligned}$$

  Hence, we must have $a>p^\sigma _{pub}$ and also $0<\left( L+\Pi _{pub,i}^\sigma \right) -p^\sigma _{pub}\left( a-p^\sigma _{pub}\right) <L$, which is what we assumed.

□

1.2 Appendix B: public company/CSR objective

Then, firm j’s objective function is

$$\begin{aligned} o_{j}^{sr}=\pi _{j}^{sr}+zCS^{sr}=\left( p-c\right) y_{j}+z\left( \sum _{i=1}^{h}ay_{i}-\frac{1}{2}y_{i}^{2}+l_{i}\right) . \end{aligned}$$

Using (4), (3) and (5), we get

$$\begin{aligned}&\left( a-\frac{y_{j}+\sum y_{-j}}{h}-c\right) y_{j}+z\left( ha\frac{ y_{j}+\sum y_{-j}}{h}-\frac{1}{2}h\left( \frac{y_{j}+\sum y_{-j}}{h}\right) ^{2}+\right. \\&\left. hL+\left( a-\frac{y_{j}+\sum y_{-j}}{h}-c\right) \left( y_{j}+\sum y_{-j}\right) -\left( a-\frac{y_{j}+\sum y_{-j}}{h}\right) \left( y_{j}+\sum y_{-j}\right) \right) . \end{aligned}$$

Simplifying and rearranging, we get equation (11).

1.3 Appendix C: proof of Proposition 3

Since consumers’ utility functions are concave, to find Pareto optimal allocations we can simply maximize a weighted average of all consumers’ utilities under feasibility and technological constraints, i.e., we want to solve the following problem: for given $a,c,L\in \mathbb {R}_{++}$, $\ \left( \gamma _{i}\right) _{i}\in \Delta ^{h-1}:=\left\{ \gamma _{i} \in \mathbb {R} _{+}^{h}:\sum _{i=1}^{h}\gamma _{i}=1\right\}$ ,

$$\begin{aligned} \begin{array}{llllll} \max _{\left( y_{i},l_{i}\right) _{i}\in \mathbb {R}^{2h}}\ \sum _{i}\gamma _{i}\left( ay_{i}-\frac{1}{2}y_{i}^{2}+l_{i}\right) &{} &{} &{} &{} &{} \\ \text {s.t.} \quad -\sum _{i}\left( cy_{i}+l_{i}\right) +hL\ge 0, &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} \end{array} \end{aligned}$$

(33)

Substitugin $y_{i}=a-c,\ l_{i}=L-c\left( a-c\right)$ in the total utility, we get

$$\begin{aligned} \begin{array}{l} \sum _{i}\left( ay_{i}-\frac{1}{2}y_{i}^{2}+l_{i}\right) =\sum _{i}\left( a\left( a-c\right) -\frac{1}{2}\left( a-c\right) ^{2}\right) +\sum _{i}l_{i}= \\ =ha\left( a-c\right) -\frac{1}{2}h\left( a-c\right) ^{2}+\sum _{i}L_{i}-hc\left( a-c\right) =hL+h\frac{1}{2}\left( a-c\right) ^{2}. \end{array} \end{aligned}$$

1.4 Appendix D: proof of Proposition 4

To get the desired result it is enough to equate total utility in the case of private (or public) companies with total utility in the Pareto optimal case. Starting with private companies, we need to find $z\in \left[ 0,1 \right]$ such that

$$\begin{aligned} hL+\frac{h\left( a-c\right) ^{2}}{2}=\frac{1}{2}\frac{hn^{2}\left( a-c\right) ^{2}}{\left[ 1+n\left( 1-z\right) \right] ^{2}}+hL \end{aligned}$$

After some manipulation, we get

$$\begin{aligned} z=\frac{\left( n+n^{2}\right) \pm \sqrt{\left( n+n^{2}\right) ^{2}-n^{2}\left( 1+2n\right) }}{n^{2}}=\frac{n+n^{2}\pm n^{2}}{ n^{2}}, \end{aligned}$$

with roots

$$\begin{aligned} z_1= & {} \frac{1}{n}\left( 2n+1\right) =\frac{1}{n}+2\\ z_2= & {} \frac{1}{n}. \end{aligned}$$

Then the desired value of z is indeed $\frac{1}{n}$.

Moving to public companies, again we need to find $z\in \left[ 0,1\right]$ such that

$$\begin{aligned} hL+\frac{h\left( a-c\right) ^{2}}{2}=\frac{nh\left( a-c\right) ^{2}\left( 1+z\right) }{2\left( n+1+nz\right) ^{2}}\left( n+nz+2\right) +hL \end{aligned}$$

But

$$\begin{aligned} \left( n+1+nz\right) ^{2}-n\left( 1+z\right) \left( n+nz+2\right) =1 \end{aligned}$$

for any value of n and z. Hence, no values of z allows to get the Pareto optimal allocation.

1.5 Appendix E: first order conditions of the mixed case with 4 firm types

Denoting, public company CSR $j_{1}$, the public company profit seeking $j_{2}$, the private company CSR as $j_{3}$ and the private companyprofit seeking as $j_{4}$. Maximization of each of their objective function yields

$$\begin{aligned} \frac{\partial o_{pubj_{1}}^{sr}}{\partial y_{pubj_{1}}^{sr}}= & {} \left( 1+z\right) \left( a-c\right) -\frac{1}{h}y_{pubj_{1}}^{sr}- \\&\frac{1}{h}\left( 1+z\right) \left[ y_{pub}^{sr}\left( m_{1}-1\right) +y_{pub}^{ps}\left( n_{1}-m_{1}-1\right) +\right. \\&y_{pr}^{sr}\left( m_{2}-1\right) +y_{pr}^{ps}\left( n_{2}-m_{2}-1\right) + \\&\left. y_{pubj_{1}}^{sr}+y_{pubj_{2}}^{ps}+y_{prj_{3}}^{sr}+y_{prj_{4}}^{ps}\right] \\= & {} 0\\ \frac{\partial \pi _{pubj_{2}}^{ps}}{\partial y_{pubj_{2}}^{ps}}= & {} \left( a-c\right) - \\&\frac{1}{h}\left[ \left( m_{1}-1\right) {y_{pub}^{sr}} +y_{pub}^{ps}\left( n_{1}-m_{1}-1\right) +\right. \\&y_{pr}^{sr}\left( m_{2}-1\right) +y_{pr}^{ps}\left( n_{2}-m_{2}-1\right) + \\&\left. y_{pubj_{1}}^{sr}+2y_{pubj_{2}}^{ps}+y_{prj_{3}}^{sr}+y_{prj_{4}}^{ps}\right] \\= & {} 0\\ \frac{\partial o_{prj_{3}}^{sr}}{\partial y_{prj_{3}}^{sr}}= & {} \left( a-c\right) -\frac{1}{h}y_{prj_{3}}^{sr}- \\&\begin{array}{l} \frac{1}{h}\left( 1+z\right) \left[ \left( m_{1}-1\right) { y_{pub}^{sr}}+y_{pub}^{ps}\left( n_{1}-m_{1}-1\right) +\right. \\ y_{pr}^{sr}\left( m_{2}-1\right) +y_{pr}^{ps}\left( n_{2}-m_{2}-1\right) + \\ \left. y_{pubj_{1}}^{sr}+2y_{pubj_{2}}^{ps}+y_{prj_{3}}^{sr}+y_{prj_{4}}^{ps} \right] \end{array}\\= & {} 0\\ \frac{\partial \pi _{prj_{4}}^{ps}}{\partial y_{prj_{4}}^{ps}}= & {} \left( a-c\right) - \\&\frac{1}{h}\left[ \left( m_{1}-1\right) {y_{pub}^{sr}} +y_{pub}^{ps}\left( n_{1}-m_{1}-1\right) +\right. \\&y_{pr}^{sr}\left( m_{2}-1\right) +y_{pr}^{ps}\left( n_{2}-m_{2}-1\right) + \\&\left. y_{pubj_{1}}^{sr}+y_{pubj_{2}}^{ps}+y_{prj_{3}}^{sr}+2y_{prj_{4}}^{ps}\right] \\= & {} 0 \end{aligned}$$

By invoking symmetry, $y_{pubj_{1}}^{sr}=y_{pub}^{sr}$, $y_{pubj_{2}}^{ps}=y_{pub}^{ps}$, $y_{prj_{3}}^{sr}=y_{pr}^{sr}$, $y_{prj_{4}}^{ps}=y_{pr}^{ps}$ and solving the system of FOCs with respect to the outputs, we obtain equations (13).

1.6 Appendix F: proof of Proposition 5

The first difference related to the internal stability shows that:

$$\begin{aligned}&\pi _{pub}^{sr}(m_{1})-\pi _{pub}^{ps}(n_{1}-m_{1}+1) \\&=\frac{hz(a-c)^{2}(1-{m_{2}}z)^{2}\left[ \left[ z({m_{1}}- {m_{2}}-1)+{n_{1}}+{n_{2}}\right] ^{2}-\left( 1+z\right) \right] }{\left[ z({m_{1}}-{m_{2}}-1)+{n_{1}} +{n_{2}}+1\right] ^{2}\left[ \left( {m_{1}}-{m_{2}} \right) z+{n_{1}}+{n_{2}}+z+1\right] ^{2}}>0, \end{aligned}$$

that is, there is not incentive to deviate from a CSR behavior for any coalition $m_{1}=1,2,\ldots ,n_{1}-1$. The second difference related to the external stability shows that

$$\begin{aligned}&\pi _{pub}^{ps}(n_{1}-m_{1})-\pi _{pr}^{sr}(m_{1}+1) \\&=-\frac{zh(a-c)^{2}(1-{m_{2}}z)^{2}\left[ \left[ z({m_{1}}- {m_{2}})+{n_{1}}+{n_{2}}\right] ^{2}-\left( 1+z\right) \right] }{\left[ \left( {m_{1}}-{m_{2}}\right) z+{n_{1}} +{n_{2}}+1\right] ^{2}\left[ \left( {m_{1}}-{m_{2}} \right) z+{n_{1}}+{n_{2}}+z+1\right] ^{2}}<0. \end{aligned}$$

Given the profit incentives, all profit seeking companies deviate to CSR.

1.7 Appendix G: proof of Proposition 6

Internal stability occurs the following inequality is positive

$$\begin{aligned}&\pi _{pr}^{sr}(m_{2})-\pi _{pr}^{ps}(n_{2}-m_{2}+1) \\&=\frac{hz(a-c)^{2}({m_{1}}z+{n_{1}}+{n_{2}})}{\left[ \left( {m_{1}}-{m_{2}}\right) z+{n_{1}}+{n_{2}} +1\right] ^{2}\left[ \left( {m_{1}}-{m_{2}}\right) z+{ n_{1}}+{n_{2}}+z+1\right] ^{2}}\times A \end{aligned}$$

where

$$\begin{aligned} A:=&z^{2}\left( {m_{1}}^{2}-{m_{1}}(2{m_{2}}({ n_{1}}+{n_{2}}+1)-1)+({m_{2}}-1)(2{m_{2}n_{1}}+2{ m_{2}n_{2}}+{m_{2}}-1)\right) \\&-z({n_{1}}+{n_{2}})(-2{m_{1}}+{m_{2}}({ n_{1}}+{n_{2}}+2)-1) \\&- \left( {m_{2}}z^{3}({m_{1}}-{m_{2}}+1)^{2}-{ m_{2}}z-({n_{1}}+{n_{2}})^{2}+1\right) >0. \end{aligned}$$

For $m<m_{I}$, where

$$\begin{aligned} m_{I}:= & {} \frac{1}{6z^{3}}\left[ 2^{2/3}\phi +2z^{2}(2{n_{2}}+2z+2 {n_{1}}(z+1)+1)\right] + \nonumber \\&\frac{1}{6z^{3}}\left[ 2\root 3 \of {2}z^{4}\left( {n_{2}}^{2}+2(z-1) {n_{2}}+z^{2}+{n_{1}}^{2}(z+1)^{2}-2z+2{n_{1}}(z+1)( {n_{2}}+z-1)+4\right) \right] \phi ^{-1} \end{aligned}$$

and $\phi :=(B+ z^{6}(C^2-D)^{\frac{1}{2}})^{\frac{1}{3}}$, with

$$\begin{aligned} B :=&-2{n_{1}}^{3}z^{9}-6{n_{1}}^{2}z^{9}-6{n_{1}} z^{9}-2z^{9}-6{n_{1}}^{3}z^{8}-6{n_{1}}^{2}z^{8}-21{ n_{1} }z^{8}-6{n_{1}}^{2}{n_{2}}z^{8}-12{n_{1}n_{2}} z^{8}-6{n_{2}}z^{8} \\&+ 6z^{8}-6{n_{1}}^{3}z^{7}+6{n_{1}}^{2}z^{7}-6{ n_{1}n_{2}}^{2}z^{7}-6{n_{2}}^{2}z^{7}-3{n_{1}}z^{7}-12{ n_{1}}^{2}{n_{2}}z^{7}-15{n_{2}}z^{7}+12z^{7}-2{n_{1}} ^{3}z^{6} \\&-2{n_{2}}^{3}z^{6}+6{n_{1}}^{2}z^{6}-6{n_{1}n_{2}} ^{2}z^{6}+6{n_{2}}^{2}z^{6}+12{n_{1}}z^{6}-6{n_{1}}^{2} {n_{2}}z^{6}+12{n_{1}n_{2}}z^{6}+12{n_{2}}z^{6}-16z^{6} \\ \\ C :=&2{n_{2}}^{3}+6(z-1){n_{2}}^{2}+3\left( 2z^{2}+5z-4\right) {n_{2}}+2{n_{1}}^{3}(z+1)^{3}+6{n_{1}}^{2}(z+1)^{2}({n_{2}}+z-1) \\&+3{n_{1}}(z+1)\left( 2{n_{2}}^{2}+4(z-1){n_{2}} +2z^{2}+5z-4\right) +2\left( z^{3}-3z^{2}-6z+8\right) \\ D :=&4\left( {n_{2}}^{2}+2(z-1){n_{2}}+z^{2}+{n_{1}} ^{2}(z+1)^{2}-2z+2{n_{1}}(z+1)({n_{2}}+z-1)+4\right) ^{3} \end{aligned}$$

External stability requires instead

$$\begin{aligned} \pi _{pr}^{ps}(n_{2}-m_{2})-\pi _{pr}^{sr}(m_{2}+1) =\frac{hz(a-c)^{2}({ n_{1}}z+{n_{1}}+{n_{2}})}{\left[ \left( n{_{1}}-{m_{2}}\right) z+{n_{1}}+{n_{2}}+1\right] ^{2}\left[ \left( n {_{1}}-{m_{2}-1}\right) z+{n_{1}}+{n_{2}}+1 \right] ^{2}}\times E \end{aligned}$$

where

$$\begin{aligned} E :=&z^{2}({n_{1}}-({m_{2}}-{n_{1}})(2{ m_{2}n_{1}}+2({m_{2}}+1){n_{2}}+{m_{2}}+{n_{1}})) \\&+z({n_{1}}+{n_{2}})({m_{2}}({n_{1}}+{n_{2}}+2)-{n_{1}}+{n_{2}}+1) \\&+ ({m_{2}}+1)z^{3}({m_{2}}-{n_{1}})^{2}-({m_{2}} +1)z-({n_{1}}+{n_{2}})^{2}+1 >0. \end{aligned}$$

For $m>m_{E}$, with

$$\begin{aligned} m_{E} :=&\frac{1}{6z^{3}}\left[ 2^{2/3}\phi +2z^{2}(2{n_{2}}+2z+2 {n_{1}}(z+1)+1)\right] -1 \\&+\frac{1}{6z^{3}}\left[ 2\root 3 \of {2}z^{4}\left( {n_{2}}^{2}+2(z-1) {n_{2}}+z^{2}+{n_{1}}^{2}(z+1)^{2}-2z+2{n_{1}}(z+1)( {n_{2}}+z-1)+4\right) \right] \phi ^{-1}. \end{aligned}$$

The existence of a parameter range that allows for a stabile coalition requires $m_{I}>m_{E}$, where $m_{I}-m_{E}=1$.

1.8 Appendix H: asymmetric technologies

An alternative approach to analyze stability is to assume that CSR companies entail a fixed cost $f>0$ to implement the CSR production strategy. Given the presence of a fixed cost of CSR activities, we may state the following result.

Proposition 13

If $z<\frac{1}{m_{2}}$, there exists $\bar{f}>0$ such that if $f\in \left( 0,\overline{f}\right)$ the industry configuration of public companies composed of a coalitions of CSR firms and a coalition of profit-seeking firms is stable.

Proof

If $z<\frac{1}{m_{2}}$, the market equilibrium outlined in (13) is admissible when, in the presence of fixed costs, CSR profits are nonnegative , i.e.,

$$\begin{aligned} \pi _{pub}^{sr}(m_1,f)= & {} \dfrac{h(1+z)(a-c)^{2}(1-{m_{2}}z)^{2}}{\left[ z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1\right] ^{2}}-f>0, \\ \pi _{pub}^{ps}(n_{1}-m_{1},f)= & {} \dfrac{h(a-c)^{2}(1-m_{2}z)\left[ z(m_{1}z+n_{1}+n_{2})+\left( 1-m_{2}z\right) \right] }{\left[ z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1\right] ^{2}}-f>0. \end{aligned}$$

Since

$$\begin{aligned} \pi _{pub}^{sr}(m_1,f)-\pi _{pub}^{ps}(n_{1}-m_{1},f)=\frac{hz(a-c)^{2}(m_{2}z-1)\left[ z(m_{1}+m_{2})+n_{1}+n_{2}-1\right] }{ \left[ z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1\right] ^{2}}>0, \end{aligned}$$

Then the condition that matters is

$$\begin{aligned} f<\bar{f}\equiv \dfrac{h(a-c)^{2}(1-m_{2}z)\left[ z(m_{1}z+n_{1}+n_{2})+\left( 1-m_{2}z\right) \right] }{\left[ z\left( m_{1}-m_{2}\right) +n_{1}+n_{2}+1\right] ^{2}}. \end{aligned}$$

□

Proposition 13 outlines the important role of fixed costs at determining a mixed industry configuration among public companies. Even if this approach is more general, it makes the problem analytically intractable and prevents to get closed-form results. The strategic interaction behind firms of different objectives and ownership remains valid and emerges more clearly in a simpler setting with symmetric technology.

1.9 Appendix I: Proof of Proposition 7

The partial derivative of (19) with respect to z is

$$\begin{aligned} \frac{\partial W }{\partial z}=\frac{h n_{1}(a-c)^{2}[n_{1}( 1+z) -n_{2}+1]}{ [n_1(1+z)+n_2+1]^3}>0, \qquad \text {for } n_{1}>\frac{n_{2}-1}{2}. \end{aligned}$$

1.10 Appendix J: Proof of Proposition 8

Differentiating $o_{j}^{sr}( z_{j},z_{-j};n_1)$ with respect to $z_{j}$ and invoking symmetry, $z_{j}=z_{-j}=z$, we get

$$\begin{aligned} \frac{\partial o_{j}^{sr}( z_{j},z_{-j};n_1) }{\partial z}=\frac{1}{2}h\left[ (a-c)^{2}\left( \frac{(n_{1}-2)z+n_{1}+n_{2}}{\left[ n_{1}(1+z) +n_2+1\right] ^{3}}-\frac{3}{\left[ n_{1}(1+z) +n_2+1\right] ^{3}}+1\right) +2L\right] >0, \end{aligned}$$

since

$$\begin{aligned} 1>\frac{3}{\left[ n_{1}(1+z) +n_2+1\right] ^{3}}. \end{aligned}$$

Therefore all public companies choose $z=1$.

1.11 Appendix K: Proof of Proposition 9

The computation of $W_{1},W_{2}$ and $W_{3}$ follows the standard strategy and yields

$$\begin{aligned} W_{1}= & {} h\frac{L\left[ n_{1}\left( 1+{z_{1}}\right) +{n_{2}} \left( 1-{z_{2}}\right) +1\right] ^{2}+2(a-c)^{2}(1-{n_{2}z_{2}})\left[ n_{1}\left( 1+{z_{1}}\right) +{n_{2}}\right] }{2\left[ n_{1}\left( 1+{z_{1}}\right) {+n_{2}}\left( 1-{z_{2}} \right) +1\right] ^{2}},\\ W_{2}= & {} h\frac{2(a-c)^{2}\left[ n_{1}\left( 1+{z_{1}}\right) +{n_{2}}\right] ^{2}+L\left[ n_{1}\left( 1+{z_{1}}\right) +{n_{2}}\left( 1-{z_{2}}\right) +1\right] ^{2}}{2\left[ n_{1}\left( 1+ {z_{1}}\right) {+n_{2}}\left( 1-{z_{2}}\right) +1\right] ^{2}},\\ W_{3}= & {} \frac{h{n_{2}}(a-c)^{2}(1-{n_{2}z_{2}})\left[ {n_{1}z_{2}}\left( 1+z_{1}\right) +1\right] }{\left[ n_{1}\left( 1+{z_{1}}\right) {+n_{2}}\left( 1-{z_{2}}\right) +1\right] ^{2}} . \end{aligned}$$

Comparing the values of $W_{1}$ with $W_{2}+W_{3}$, we get

$$\begin{aligned} W_{1}-\left( W_{2}+W_{3}\right)= & {} \\&-\frac{h(a-c)^{2}\left[ {n_{1}^{2}}\left( 1+z_{1}\right) ^{2}-{n_{1}}\left( 1+z_{1}\right) \left( {n_{2}}({z_{2}}({n_{2}z_{2}}-2)-2)+1\right) +{n_{2}^{2}}\right] }{\left[ n_{1}\left( 1+{z_{1}}\right) {+n_{2}}\left( 1-{z_{2}}\right) +1 \right] ^{2}}. \end{aligned}$$

The sign is the square brackets of the numerator, which can be rewritten as

$$\begin{aligned}&n_{1}n_{2}^{2}\left( 1+z_{1}\right) z_{2}^{2}-2n_{1}n_{2}\left( 1+z_{1}\right) z_{2} \\&-n_{1}^{2}\left( 1+z_{1}\right) ^{2}-2n_{1}n_{2}\left( 1+z_{1}\right) +n_{1}\left( 1+z_{1}\right) -n_{2}^{2}. \end{aligned}$$

It is a second degree polynomial in $z_{2}$, with the following roots:

$$\begin{aligned} \rho _{1}= & {} \frac{{n_{1}n_{2}}\left( 1+z_{1}\right) -\sqrt{{ n_{1}n_{2}^{2}}\left( 1+z_{1}\right) ({n_{1}z_{1}}+{n_{1}}+ {n_{2}})^{2}}}{{n_{1}n_{2}^{2}}\left( 1+z_{1}\right) }<0,\\ \rho _{2}= & {} \frac{{n_{1}n_{2}}\left( 1+z_{1}\right) +\sqrt{{n_{1}n_{2}^{2}}\left( 1+z_{1}\right) ({n_{1}z_{1}}+{n_{1}}+ {n_{2}})^{2}}}{{n_{1}n_{2}^{2}}\left( 1+z_{1}\right) }>0. \end{aligned}$$

Since one root is negative and the other is positive and since $z_{2}\in \left[ 0,\widehat{z}_{2}\right)$, to show that $W_{1}<W_{2}+W_{3}$, it suffices to show that the positive root is larger than $\widehat{z}_{2}$, i.e.,

$$\begin{aligned} \rho _{2}-\frac{1}{n_{2}}=\frac{({n_{1}z_{1}}+{n_{1}}+{ n_{2}})^{2}}{\sqrt{{n_{1}n_{2}}^{2}\left( 1+z_{1}\right) ({n_{1}z_{1}}+{n_{1}}+{n_{2}})^{2}}}>0, \end{aligned}$$

which is certainly true.

1.12 Appendix L: Proof of Proposition 10

Since

$$\begin{aligned} \frac{\partial W\left( y_{i}^{sr},y_{d}^{ps}\right) }{\partial z_{1}}=\frac{ hn_{1}(a-c)^{2}(1-{n_{2}z_{2}})^{2}\left[ n_{1}(1+z_{1})-n_{2}(1-z_{2})+1\right] }{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{3}}, \end{aligned}$$

and since we chose $z_{2}=\overline{z}_{2}\in \left( 0,\frac{1}{n_{2}} \right)$, we have $\frac{\partial W\left( y_{i}^{sr},y_{d}^{ps}\right) }{ \partial z_{1}}\ge 0$ if and only if

$$\begin{aligned} z_{1}\ge \hat{z}_{1}=\frac{n_{2}(1-\overline{z}_{2})-\left( n_{1}+1\right) }{n_{1}}. \end{aligned}$$

We have to distinguish 3 cases.

Case 1. $\widehat{z}_{1}\le 0$, then $n_{1}\ge n_{2}(1-\overline{z }_{2})-1.$

Then, $\frac{\partial W\left( y_{i}^{sr},y_{d}^{ps}\right) }{\partial z_{1}} \ge 0$ if $z_{1}\in \left[ 0,1\right]$ and then the optimal choice of $z_{1}$ is 1.

Case 2. $\widehat{z}_{1}\in \left( 0,1\right)$.

In this case, we have $n_{2}(1-\overline{z}_{2})-\left( n_{1}+1\right) >0$ and $n_{2}(1-\overline{z}_{2})-\left( n_{1}+1\right) <n_{1}$, i.e.,

$n_{1}<n_{2}(1-\overline{z}_{2})-1$ and $n_{1}>\frac{1}{2}\left[ n_{2}\left( 1-\overline{z}_{2}\right) -1\right]$. Then, $\frac{\partial W\left( y_{i}^{sr},y_{d}^{ps}\right) }{\partial z_{1}}\le 0$ if $z_{1}\in \left[ 0, \widehat{z}_{1}\right]$, and the optimal choice of $z_{1}$ can be found comparing $W\left( z_{1}=0,z_{2}=\overline{z}_{2}\right)$ with $W\left( z_{1}=1,z_{2}=\overline{z}_{2}\right)$. We get

$$\begin{aligned} W\left( z_{1}=0,z_{2}=\overline{z}_{2}\right)= & {} \frac{h(a-c)^{2}\left[ n_{1}^{2}+n_{1}\left( {n_{2}}\left( 2-{n_{2}\overline{z} _{2}^{2} }\right) +1\right) +{n_{2}}(-2{n_{2}\overline{z}_{2}} +{n_{2}}+2)\right] }{({n_{1}}-{n_{2}\overline{z}_{2}}+ {n_{2}}+1)^{2}}+L, \\ W\left( z_{1}=1,z_{2}=\overline{z}_{2}\right)= & {} \frac{h(a-c)^{2}\left[ \left( 4{n_{1}^{2}}+{n_{1}}\left( -2{n_{2}^{2}\overline{z }_{2}^{2}}+4{n_{2}}+2\right) +{n_{2}}(-2{n_{2}\overline{ z}_{2}}+{n_{2}}+2)\right) \right] }{(2{n_{1}}-{n_{2} \overline{z}_{2}}+{n_{2}}+1)^{2}}+L, \end{aligned}$$

where

$$\begin{aligned}&W\left( z_{1}=0,z_{2}=\overline{z}_{2}\right) -W\left( z_{1}=1,z_{2}= \overline{z}_{2}\right) \\&= - \frac{h{n_{1}}(a-c)^{2}({n_{2}\overline{z}_{2}}-1)^{2}\left[ 2 {n_{1}^{2}}+3{n_{1}}-{n_{2}^{2}}({\overline{z}_{2}}-1)^{2}+1\right] }{({n_{1}}-{n_{2}\overline{z}_{2}}+ {n_{2}}+1)^{2}(2{n_{1}}-{n_{2}\overline{z}_{2}}+{n_{2}}+1)^{2}}, \end{aligned}$$

whose sign is in

$$\begin{aligned} -2{n_{1}^{2}}-3{n_{1}}+{n_{2}^{2}}(1-{\overline{z}_{2}})^{2}-1, \end{aligned}$$

which is a quadratic and concave function on $n_{1}$ with values internal to the roots. The positive root is

$$\begin{aligned} \widehat{n}_{1}\equiv \frac{1}{4}\left[ \left( 8n_{2}^{2}(1-\overline{z} _{2})^{2}+1\right) ^{\frac{1}{2}}-3\right] . \end{aligned}$$

Hence, if $n_{1}\le \widehat{n}_{1}$, then the government chooses $z_{1}=0$ . If $n_{1}>\widehat{n}_{1}$, the government chooses $z_{1}=1$.

Case 3. $\widehat{z}_{1}\ge 1$, i.e., $n_{1}\le \frac{1}{2}\left[ n_{2}\left( 1-\overline{z}_{2}\right) -1\right] .$

Then, $\frac{\partial W\left( y_{i}^{sr},y_{d}^{ps}\right) }{\partial z_{1}} \le 0$ if $z_{1}\in \left[ 0,1\right]$ and then government chooses $z_{1}=0$.

Comparing the three thresholds I get

$$\begin{aligned} n_{2}(1-\overline{z}_{2})-1-\widehat{n}_{1}\varpropto 8n_{2}(1-\overline{z} _{2})\left[ n_{2}(1-\overline{z}_{2})-1\right] >0, \end{aligned}$$

and

$$\begin{aligned} \widehat{n}_{1}-\frac{1}{2}\left[ n_{2}\left( 1-\overline{z}_{2}\right) -1 \right] \varpropto 4n_{2}\left[ n_{2}(1-\overline{z}_{2})-1\right] (1- \overline{z}_{2})>0. \end{aligned}$$

Therefore the only relevant threshold on $n_{1}$ to determine the government choice is $\widehat{n}_{1}$.

1.13 Appendix M: Proof of Corollary 3

Differentiating each component of welfare with respect to $z_{1}$, we get

$$\begin{aligned} \frac{\partial W_{1}}{\partial z_{1}}= & {} -\frac{h{n_{1}} (a-c)^{2}\left( 1-{n_{2}z_{2}}\right) \left[ {n_{1}}\left( 1+ {z_{1}}\right) +{n_{2}}\left( 1+{z_{2}}\right) -1\right] }{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1 \right] ^{3}}<0, \\ \frac{\partial W_{1}}{\partial z_{2}}= & {} -\frac{h{n_{2}}(a-c)^{2} \left[ {n_{1}}\left( {1+z_{1}}\right) +{n_{2}}\right] \left[ {n_{1}}\left( {1+z_{1}}\right) +{n_{2}}\left( {1+z_{2}}\right) -1\right] }{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{3}}<0, \\ \frac{\partial W_{2}}{\partial z_{1}}= & {} \frac{2h{n_{1}} (a-c)^{2}\left( 1-{n_{2}z_{2}}\right) \left[ {n}\left( { _{1}1+z_{1}}\right) +{n_{2}}\right] }{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{3}}>0, \\ \frac{\partial W_{2}}{\partial z_{2}}= & {} \frac{2h{n_{2}}(a-c)^{2} \left[ {n_{1}}\left( {1+z_{1}}\right) +{n_{2}}\right] ^{2}}{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{3}}>0, \\ \frac{\partial W_{3}}{\partial z_{1}}= & {} -\frac{h{n_{1}n_{2}} (a-c)^{2}\left( 1-{n_{2}z_{2}}\right) \left[ {z_{2}}\left[ {n_{1}}\left( 1+{z_{1}}\right) -\left( {n_{2}}+1\right) \right] +{n_{2}z_{2}^{2}}+2\right] }{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{3}}<0, \\ \frac{\partial W_{3}}{\partial z_{2}}= & {} -\frac{h{n_{2}}(a-c)^{2} \left[ {n_{1}}\left( {1+z_{1}}\right) +{n_{2}}\right] \left[ {n_{1}}({z_{1}}+1)\left( 2{n_{2}z_{2}}-1\right) + {n_{2}z_{2}}+{n_{2}}-1\right] }{\left[ {n_{1}}\left( 1+z_{1}\right) +n_{2}\left( 1-z_{2}\right) +1\right] ^{3}}, \end{aligned}$$

with $\frac{\partial W_{3}}{\partial z_{2}}<0$ if

$$\begin{aligned} n_{1}<\frac{1-n_{2}(1+z_{2})}{(1+z_{1})(2n_{2}z_{2}-1)}. \end{aligned}$$