Optimal stopping time, consumption, labour, and portfolio decision for a pension scheme

Abstract

In this work we solve in a closed form the problem of an agent who wants to optimise the inter-temporal recursive utility of both his consumption and leisure by choosing: (1) the optimal inter-temporal consumption, (2) the optimal inter-temporal labour supply, (3) the optimal share of wealth to invest in a risky asset, and (4) the optimal retirement age. The wage of the agent is assumed to be stochastic and correlated with the risky asset on the financial market. The problem is split into two sub-problems: the optimal consumption, labour, and portfolio problem is solved first, and then the optimal stopping time is approached. We compute the solution through both the so-called martingale approach and the solution of the Hamilton–Jacobi–Bellman partial differential equation. In the numerical simulations we compare two cases, with and without the opportunity, for the agent, to work after retirement, at a lower wage rate.

1 Introduction

According to the Finnish Centre for Pensions,¹ in the EU15 countries, the average retirement age is 65 years. Instead, in the other 12 EU countries, the retirement age is lower, but it is planned to be raised to the same level over the next decade. Furthermore, Germany, Denmark, France, and Spain have decided to increase the retirement age from 65 to 67 years, while the goal is 68 years in both UK and Ireland.

Most of the changes in retirement ages are scheduled for the 2020s. In Italy, the Netherlands, Finland, Cyprus, Denmark, Greece, Portugal, UK and Slovakia, the retirement age will be linked to the development of the life expectancy.

“European pension systems are facing the dual challenge of remaining financially sustainable and being able to provide Europeans with an adequate income in retirement” (European Commission 2017). Actually, life expectancy after the age of 70 has been constantly increasing over the last decades, generating the so-called “longevity risk” (European Commission 2018a). Thus, without a counterbalance increase in the retirement age, the level of contributions paid by the workers, could not be able to suitably finance the pensions that will have to be paid for increasingly longer period of time.

Combined to this, the calculation of the optimal retirement age plays a crucial role (Farhi and Panageas 2007). Let us assume a worker that must decide the level of consumption for the coming years including the retirement period, given his level of wealth. This agent would be exposed to both market risks and mortality risk. In this work we study the problem of such an agent whose wage, investment opportunities, and death are all stochastic. We show that a part of the optimal strategy for the agent is to invest in a life annuity and to borrow against his human capital.

It is well known that social security wealth,² which typically constitutes the biggest share of a retiree’s wealth, comes in an annuitised form. In some countries, annuity markets are growing, especially in UK where pension schemes have transferred $\pounds$135bn of liabilities to insurers over the last decade, and this is set to quadruple over the next 10 years,³ while in the US the annuity market is around 234 billion dollars.⁴

In this work we do not take into account any pension scheme. Instead, we investigate the choice of an agent who can only rely on both his wage and his financial investments. Actually, in some countries, future retirees will have to rely less on social security schemes and more on funded pension plans (Feldstein and Siebert 2002; Diamond and Orszag 2005; Rusconi 2008), which mostly leave to each individual the choice between annuitising and cashing-out pension wealth at retirement.

There exists a wide literature about optimal investment in financial market and annuitisation, and it mainly refers to life cycle frameworks with uncertainty. Benitez-Silva (2000) presents a dynamic model of labour/leisure, consumption/saving, considering additional sources of uncertainty, introducing annuities and Social Security, and providing a general framework which allows for policy experimentation in a life cycle model. Friedman and Warshawsky (1990), focus on annuity pricing in order to explain the almost nonexistence of a market for these instruments and do not consider investment uncertainty. Longevity uncertainty and purchase of annuities is taken into account in Brugiavini (1993) in a two/three period model with different behaviour of employees and entrepreneurs. Mitchell et al. (1999) calculate the expected present value of the annuities by using the term structure of interest rate rather than a fixed interest rate, and they find that retirees should value annuities even if they are not actuarially fair. Brown (1999a, b), introduce uncertainty and use data on older Americans to construct a measure of the consumer’s valuation of additional annuitisation and to test the hypothesis that old individuals purchase term insurance to offset the excessive annuitisation imposed by the government social programs. Kotlikoff and Spivak (1981) study the role of the family as an incomplete annuities market, with the annuity decision made at exogenous points in time. Eichenbaum and Peled (1987) analyse the over accumulation of private capital in a two period model of competitive annuities with adverse selection. Recently, Menoncin and Regis (2017) found that individuals should optimally invest a large fraction of their wealth in longevity linked assets in the pre-retirement phase, because of their need to hedge against stochastic fluctuations in their remaining lifetime at retirement. In a two period framework, Magnani (2020) studies the optimal retirement problem for an agent who can also chose how to save from his/her (risky) salary.

In line with the previous statements, in this paper we solve the problem of a representative agent who must decide, at the same time: (1) how much to work, (2) how much to invest on financial market, (3) how much to consume, and (4) when to retire. The agent’s time horizon coincides with his death time and the optimisation problem is subject to some risks: (1) the market risk on the financial market (mainly price risk), (2) the mortality risk on agent’s lifetime, and (3) the wage risk on agent’s wealth.

We model the risk through a Wiener process and we solve the problem to maximise the expected utility of agent’s inter-temporal consumption and leisure (defined as nonworking hours). After retirement, we assume the agent is still able to work, but he will receive a fraction of the wage. Of course, the agent must finance his consumption over his whole life time. The utility of leisure is assumed to be proportional to agent’s received wage and, accordingly, reduces after retirement. Here, we define the human capital as the total expected discount value of future wages.

This work builds on the same framework studied in Menoncin (2008) and Menoncin and Regis (2017). In both these papers, a longevity linked security is listed on a complete arbitrage-free financial market, but the retirement age is compulsory. Instead, here we take into account only the mortality risk, but we solve the problem of the optimal retirement age. We use a two step approach: first we find the optimal consumption, labour supply, and portfolio for any possible (stochastic) stopping time, then we compute the optimal stopping time by maximising the value function that solves the first problem. We solve the problem by using both the so-called martingale approach and the Hamilton–Jacobi–Bellman partial differential equation.

The framework of an optimal stopping time problem is often applied to the real options,⁵ when an irrevocable decision must be taken. Actually, also in this case, the decision to retire cannot be called off and it permanently affects the dynamics of agent’s problem. Bodie et al. (1992) suggested that “one current research objective is to analyse the retirement problem as an optimal stopping problem and to evaluate the accompanying portfolio effects”. Also Kula (2003) wrote that “the retirement decision may be treated as an investment process: first we collect capital/retirement wealth, and if we have accumulated enough we invest/retire, depending on the actual and expected prices/wages”. Finally, Farhi and Panageas (2007) extended Bodie et al. (1992) in a optimal stopping problem, also focusing on the “importance of the real option to retire for portfolio choice”.

In solving our problem we must assume that the market is complete. This means that the agent is able to borrow against his future wages (human capital) and any risk on the financial market can be perfectly hedged through a suitable portfolio.

When we turn to the second problem, that is the optimal stopping problem, we are able to find a closed form solution only if we assume that the inter-temporal preference parameter coincides with the risk aversion parameter. Under this hypothesis, the value function of the second problem can be written in closed form as a function of a wage threshold. When this threshold is crossed, then the agent finds it optimal to retire.

Finally, we calibrate our model to the US data and we present some numerical results that allow to investigate the dynamic behaviour of the optimal consumption, labour supply, and portfolio.

In the simulations we study two cases: (A) when the agent is not allowed to work any longer after retirement and so his salary immediately drops to zero, and (B) when the agent is still allowed to work but at a reduced salary (one third of the original salary).

We show that the optimal retirement should happen after about 50 years of working (on average) in case A and 35 years in case B. If we assume that an agent begins working when he is about 25, this choice implies a retirement age that is close to the statutory value in case A, but which is much lower than the statutory age in case B. The optimal labour supply is of course higher in case A then in case B, while in case B it remains positive even for a very old age.

Furthermore, we show that cases A and B differ a lot also for the optimal choice of consumption and portfolio. In case B both optimal values are monotonic function of time. In particular, the optimal consumption is a reducing fraction of wealth over time, while the optimal portfolio is an increasing function of time. This last result suggests that agent should invest in a less risky portfolio when they are young, and increase the risky proportion when they grow older. This result is definitely different in case A: the fact that the agent cannot count any longer on a wage after retirement, deeply modify his portfolios strategy. The optimal portfolio composition is highly volatile during the middle age of the agent, while after retirement the percentage of risky asset becomes constant. In fact, when there is no more (wage) risk to hedge against, the optimal portfolio is just given by its speculative component.

In case A, the optimal consumption ratio is decreasing over time for a young agent, but then it starts increasing and it becomes constant after retirement. In fact, we know from the literature, that without labour income, and with constant relative risk aversion preferences, the optimal consumption is a constant percentage of wealth.

The remaining of the paper is organised as follows: Sect. 2 shows the framework, Sect. 3 presents the result of the first problem, i.e. the optimal consumption, labour supply, and portfolio. Section 4 shows the optimal stopping problem, and solves it in closed form. Section 5 presents a numerical simulation calibrated on the US data. Section 6 concludes, and some technical results are gathered in three appendices.

2 The model setup

2.1 Financial market

On a continuously open and friction-less financial market over the time set $[t_{0},+\infty [$, one risky asset is traded, and its price $S_{t}\in {{\mathbb{R}}}_{+}$ follows a geometric Brownian motion

$$\begin{aligned} \frac{dS_{t}}{S_{t}}=\mu dt+\sigma dW_{t}, \end{aligned}$$

(1)

where both the expected return ($\mu$) and the volatility ($\sigma$) are constant, and $W_{t}$ is a Wiener processes (with zero mean and variance t). The initial asset price $S_{t_{0}}$ is known. Also a risk-less asset is listed and its price $G_{t}$ solves the ordinary differential equation

$$\begin{aligned} \frac{dG_{t}}{G_{t}}=rdt, \end{aligned}$$

(2)

where r is the risk-less interest rate. We assume $G_{t_{0}}=1$, i.e. the risk-less asset is the numéraire of the economy.

This financial market is arbitrage free and complete. In other words, there exists a unique market price of risk $\xi$ such that $\sigma \xi =\mu -r$.

Girsanov’s theorem allows us to switch from the historical (${{\mathbb{P}}}$) to the risk-neutral probability ${{\mathbb{Q}}}$ by using $dW_{t}^{{\mathbb{Q}}}=\xi dt+dW_{t}$. The value in $t_{0}$ of any cash flow $\Xi _{t}$ available at time t can be written as

$$\begin{aligned} \Xi _{t_{0}}={{\mathbb{E}}}_{t_{0}}^{{\mathbb{Q}}}\left[ \Xi _{t}\frac{G_{t_{0}}}{G_{t}}\right] ={{\mathbb{E}}}_{t_{0}}^{{\mathbb{Q}}}\left[ \Xi _{t}e^{-r\left( t-t_{0}\right) }\right] ={{\mathbb{E}}}_{t_{0}}\left[ \Xi _{t}m_{t_{0},t}e^{-r\left( t-t_{0}\right) }\right] , \end{aligned}$$

(3)

where ${{\mathbb{E}}}_{t_{0}}\left[ \bullet \right]$ and ${{\mathbb{E}}}_{t_{0}}^{{\mathbb{Q}}}\left[ \bullet \right]$ are the expected value operators under the historical (${{\mathbb{P}}}$) and the risk neutral (${{\mathbb{Q}}}$) probabilities respectively, conditional on the information set at time $t_{0}$, and the martingale $m_{t_{0},t}$, such that $m_{t_{0},t_{0}}=1$, solves

$$\begin{aligned} \frac{dm_{t_{0},t}}{m_{t_{0},t}}=-\xi dW_{t}. \end{aligned}$$

(4)

2.2 Agent’s wage

In this framework, we assume that the agent (household) works for the firm whose stocks are listed on the financial market, and this firm pays an instantaneous wage $w_{t}$ to the agent. Thus, the risk source that drives the price $S_{t}$ is the same that drives the wage. Accordingly, we assume that $w_{t}$ solves the following differential equation:

$$\begin{aligned} \frac{dw_{t}}{w_{t}}=\mu _{w}dt+\sigma _{w}dW_{t}. \end{aligned}$$

(5)

The agent can choose how much to work ($l_{t}$) at any instant and, accordingly, his instantaneous wage will be $l_{t}w_{t}$. The agent optimally chooses when to retire (at time T), and after retirement he can still work, bu he will receive a percentage ($\omega$) of the wage $w_{t}$. Thus, the labour income for the agent is given by following formula

$$\begin{aligned}&w_{t}l_{t}{{\mathbb{I}}}_{t<T}+\omega w_{t}l_{t}\left( 1-{{\mathbb{I}}}_{t<T}\right) \\ =\,&w_{t}l_{t}\left( {{\mathbb{I}}}_{t<T}+\omega \left( 1-{{\mathbb{I}}}_{t<T}\right) \right) \\ :=\,&w_{t}l_{t}\omega _{t} \end{aligned}$$

in which ${{\mathbb{I}}}_{\varepsilon }$ is the indicator function of the event $\varepsilon$ whose value is 1 if the event happens and 0 otherwise. This means that the labour income is $w_{t}l_{t}$ before retirement, while it becomes $\omega w_{t}l_{t}$ after retirement. Furthermore, we commit a slight abuse of notation by defining $\omega _{t}$ the ‘dynamic’ version of $\omega$. Here, in particular, we set $\omega _{t}=1$ when $t<T$ and $\omega _{t}=\omega$ when $t\ge T$.

In the numerical simulations we will show the difference in the final results when $\omega =0$ and $\omega \ne 0$. These two cases can be dealt together in the theoretical framework, and, nevertheless, they are characterised by a very different behaviour of the optimal agent’s strategy (in terms of retirement age, consumption, and portfolio).

2.3 The mortality risk

The agent is aged x at $t_{0}$ and he dies at a random time $\Omega \in [t_{0},\infty [$. If we call $\lambda _{t}$ the force of mortality, his probability to be alive at time t, given that he is alive at time $t_{0}$, is

$$\begin{aligned} {{\mathbb{P}}}\left\{ \left. \Omega>t\right| \Omega>t_{0}\right\} ={{\mathbb{E}}}_{t_{0}}\left[ {{\mathbb{I}}}_{\Omega >t}\right] =e^{-\int _{t_{0}}^{t}\lambda _{u}du}, \end{aligned}$$

(6)

where we have used the property that the expected value of the indicator function of an event is the probability of that event.

2.4 The human capital

In this framework, the human capital is defined as the expected present value of future wages that the agent will obtain during his working life.

If we define $\Psi _{t_{0}}$ such a human capital at time $t_{0}$, we can compute it as follows:

$$\begin{aligned} \Psi _{t_{0}}\left( T\right)&:={{\mathbb{E}}}_{t_{0}}^{{\mathbb{Q}}}\left[ \int _{t_{0}}^{\infty }\omega _{t}w_{t}e^{-\int _{t_{0}}^{t}\lambda _{s}ds-r\left( s-t_{0}\right) }dt\right] \\&={{\mathbb{E}}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }\omega _{t}w_{t}m_{t_{0},t}e^{-\int _{t_{0}}^{t}\lambda _{s}ds-r\left( s-t_{0}\right) }dt\right] .\nonumber \end{aligned}$$

(7)

The human capital is computed under the risk neutral probability since it measures a kind of “market power” for the agent. In the complete market of our framework, the agent can trade his human capital. Accordingly, his disposable income is not only the current wage, but also the future flow of wages.

If we use the property of the indicator function ${{\mathbb{I}}}_{t<T}=1-{{\mathbb{I}}}_{t\ge T}$, the human capital can be written as

$$\begin{aligned} \Psi _{t_{0}}\left( T\right) =\,&{{\mathbb{E}}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }w_{t}m_{t_{0},t}e^{-\int _{t_{0}}^{t}\lambda _{s}ds-r\left( s-t_{0}\right) }dt\right] \\&-{{\mathbb{E}}}_{t_{0}}\left[ \int _{T}^{\infty }\left( 1-\omega \right) w_{t}m_{t_{0},t}e^{-\int _{t_{0}}^{t}\lambda _{s}ds-r\left( s-t_{0}\right) }dt\right] , \end{aligned}$$

in which the subtrahend is the human capital which the agent renounces to when he decides to retire.

2.5 The investor’s wealth

The investor holds a portfolio given by $\theta _{G,t}\in {{\mathbb{R}}}$ quantities of the risk-less asset and $\theta _{t}\in {{\mathbb{R}}}$ quantities of the risky asset. Thus, at any instant in time the value of his wealth $R_{t}$ is given by

$$\begin{aligned} R_{t}=\theta _{G,t}G_{t}+\theta _{t}S_{t}. \end{aligned}$$

(8)

Negative values of $\theta _{G,t}$ and $\theta _{t}$ indicate short selling. The differential of this constraint is

$$\begin{aligned} dR_{t}=\theta _{G,t}dG_{t}+\theta _{t}dS_{t}+\left( d\theta _{G,t}\left( G_{t}+dG_{t}\right) +d\theta _{t}\left( S_{t}+dS_{t}\right) \right) , \end{aligned}$$

(9)

where the term in brackets must:

• finance the agent’s consumption $c_{t}dt$,

• be financed by the agent’s salary during his working life $\omega _{t}w_{t}l_{t}dt$,

• finance the loss in wealth due to death: $\lambda _{t}R_{t}dt$.

Thus, the dynamic constraint can be written as

$$\begin{aligned} dR_{t}=\theta _{G,t}dG_{t}+\theta _{t}dS_{t}-c_{t}dt+\omega _{t}w_{t}l_{t}dt+\lambda _{t}R_{t}dt, \end{aligned}$$

and if $\theta _{G,t}$, $dS_{t}$, and $dG_{t}$ are substituted from (8), (1), and (2) respectively, we obtain

$$\begin{aligned} dR_{t}=\left( R_{t}\left( r+\lambda _{t}\right) +\theta _{t}S_{t}\left( \mu -r\right) -c_{t}+\omega _{t}w_{t}l_{t}\right) dt+\theta _{t}S_{t}\sigma dW_{t}. \end{aligned}$$

(10)

Note that under the risk neutral probability, (10) can be written as

$$\begin{aligned} dR_{t}&=\left( R_{t}\left( r+\lambda _{t}\right) +\theta _{t}S_{t}\left( \mu -r\right) -c_{t}+\omega _{t}w_{t}l_{t}\right) dt+\theta _{t}S_{t}\sigma \left( dW_{t}^{{\mathbb{Q}}}-\xi dt\right) \\&=\left( R_{t}\left( r+\lambda _{t}\right) -c_{t}+\omega _{t}w_{t}l_{t}\right) dt+\theta _{t}S_{t}\sigma dW_{t}^{{\mathbb{Q}}}, \end{aligned}$$

and it implies that the initial wealth must be

$$\begin{aligned} R_{t_{0}}={{\mathbb{E}}}_{t_{0}}^{{\mathbb{Q}}}\left[ \int _{t_{0}}^{\infty }\left( c_{t}-\omega _{t}w_{t}l_{t}\right) e^{-\int _{t_{0}}^{t}r+\lambda _{u}du}dt\right] , \end{aligned}$$

and this is actually the constraint that we will use for solving the optimisation problem of the agent.

2.6 Agent’s preferences

We assume that the preferences of the agent can be represented through a recursive utility function $U_{t}$ having the following form:

$$\begin{aligned} U_{t}={{\mathbb{E}}}_{t}\left[ \int _{t}^{\infty }f\left( c_{s},l_{s},U_{s}\right) ds\right] , \end{aligned}$$

in which the function f is the so called Esptein-Zin ‘aggregator’. Inside the aggregator, we assume that consumption and labour are additive. In particular, we adopt the following parametrisation used in Duffie and Epstein (1992):

$$\begin{aligned} f\left( c_{t},l_{t},U_{t}\right):=\, & \left( \frac{\left( c_{t}-c_{m}\right) ^{1-\frac{1}{\phi }}}{1-\frac{1}{\phi }}+\chi _{t}\frac{\left( L-l_{t}\right) ^{1-\frac{1}{\phi }}}{1-\frac{1}{\phi }}\right) \left( \left( 1-\delta \right) U_{t}\right) ^{1-\frac{1-\frac{1}{\phi }}{1-\delta }}\\&-\left( \rho +\lambda _{t}\right) \frac{1-\delta }{1-\frac{1}{\phi }}U_{t}, \end{aligned}$$

whose elements are described in what follows.

• $c_{m}$ is the subsistence level of consumption. We assume that the agent takes utility only from consumption that exceeds this minimum level; in fact, it will be optimal to consume always more than $c_{m}$. We stress that preferences of consumption belong to the Hyperbolic Absolute Risk Aversion (HARA) family.

• L is the maximum number of working hours that the agent can supply and, thus, the difference $L-l_{t}$ is the leisure time.

• $\chi _{t}:=w_{t}\omega _{t}\left( \chi _{A}{{\mathbb{I}}}_{t<T}+\chi _{B}\left( 1-{{\mathbb{I}}}_{t<T}\right) \right)$ is the relative weight of the leisure utility with respect to the consumption utility. We assume that the leisure utility during retirement has a different weight ($\chi _{B}$) than leisure utility during working life ($\chi _{A}$). Furthermore, the utility of the leisure is weighted by the salary $w_{t}$ (reduced by a percentage after retirement) for modelling the attitude of the agent towards leisure, which usually gives higher utility when the wage is higher.

• $\rho$ is the (constant) subjective discount rate.

• $\delta$ and $\phi$ are, respectively, the Arrow-Pratt relative risk aversion parameter and the elasticity of inter-temporal substitution. We highlight that if $\frac{1}{\phi }=\delta$ then the utility function collapses to the usual time separable utility with constant relative risk aversion (in which the inter-temporal preferences and the risk aversion are not disentangled). In fact, under this hypothesis

  $$\begin{aligned} U_{t}={{\mathbb{E}}}_{t}\left[ \int _{t}^{\infty }\left( \frac{\left( c_{s}-c_{m}\right) ^{1-\delta }}{1-\delta }+\chi _{s}\frac{\left( L-l_{s}\right) ^{1-\delta }}{1-\delta }-\left( \rho +\lambda _{s}\right) U_{s}\right) ds\right] , \end{aligned}$$

  whose expected differential is

  $$\begin{aligned} {{\mathbb{E}}}_{t}\left[ dU_{t}\right] =\left( \left( \rho +\lambda _{t}\right) U_{t}-\left( \frac{\left( c_{t}-c_{m}\right) ^{1-\delta }}{1-\delta }+\chi _{t}\frac{\left( L-l_{t}\right) ^{1-\delta }}{1-\delta }\right) \right) dt, \end{aligned}$$

  and whose solution is

  $$\begin{aligned} U_{t}={{\mathbb{E}}}_{t}\left[ \int _{t}^{\infty }\left( \frac{\left( c_{s}-c_{m}\right) ^{1-\delta }}{1-\delta }+\chi _{s}\frac{\left( L-l_{s}\right) ^{1-\delta }}{1-\delta }\right) e^{-\rho \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] . \end{aligned}$$

Finally, the optimisation problem can be written as follows:

$$\begin{aligned} \max _{\left\{ c_{t},l_{t},\theta _{t}\right\} _{t\in [t_{0},\infty [},T}&{{\mathbb{E}}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }f\left( c_{t},l_{t},U_{t}\right) dt\right] . \end{aligned}$$

(11)

3 The optimal consumption, portfolio, and labour

In order to compute the optimal solution to Problem (11), we split it into two sub-problems. The idea is to follow a three step procedure.

• 1. First step: optimising with respect to consumption, labour supply, and portfolio, given any possible pension time T. In optimising this part of the problem, we treat T as a stochastic variable.

• 2. Second step: computing the value function of the problem as a function of the stochastic variable T.

• 3. Third step: optimising the value function with respect to T.

The solution to the first step is shown in the following proposition.

Proposition 1

Given the stochastic pension time T, the optimal consumption, portfolio, and labour supply that solve Problem (11) given (5) and (10) are

$$\begin{aligned}&c_{t}^{*}=c_{m}+\frac{R_{t}-H_{t}}{F_{t}^{\frac{1-\phi }{1-\frac{1}{\delta }}}}, \end{aligned}$$

(12)

$$\begin{aligned}&l_{t}^{*}=L-\left( \frac{\chi _{t}}{\omega _{t}w_{t}}\right) ^{\phi }\frac{R_{t}-H_{t}}{F_{t}^{\frac{1-\phi }{1-\frac{1}{\delta }}}}, \end{aligned}$$

(13)

$$\begin{aligned}&S_{t}\theta _{t}^{*}=\frac{R_{t}-H_{t}}{\delta }\frac{\mu -r}{\sigma ^{2}}+\frac{w_{t}\sigma _{w}}{\sigma }\left( \frac{\partial H_{t}}{\partial w_{t}}+\frac{R_{t}-H_{t}}{F_{t}}\frac{\partial F_{t}}{\partial w_{t}}\right) , \end{aligned}$$

(14)

in which

$$\begin{aligned}&H_{t}:={{\mathbb{E}}}_{t}^{{\mathbb{Q}}}\left[ \int _{t}^{\infty }\left( c_{m}-\omega _{s}w_{s}L\right) e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] , \end{aligned}$$

(15)

$$\begin{aligned}&F_{t}:={{\mathbb{E}}}_{t}^{{\mathbb{Q}}_{\delta }}\left[ \left( \int _{t}^{\infty }\left( 1+\chi _{t}^{\phi }\left( \omega _{s}w_{s}\right) ^{1-\phi }\right) e^{-\left( \left( 1-\phi \right) r+\phi \rho +\frac{1-\phi }{\delta }\frac{1}{2}\left( \frac{\mu -r}{\sigma }\right) ^{2}\right) \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right) ^{\frac{1-\frac{1}{\delta }}{1-\phi }}\right] , \end{aligned}$$

(16)

and

$$\begin{aligned}&dW_{t}^{{\mathbb{Q}}}=\frac{\mu -r}{\sigma }dt+dW_{t},\\&dW_{t}^{{\mathbb{Q}}_{\delta }}=\frac{\delta -1}{\delta }\frac{\mu -r}{\sigma }dt+dW_{t}. \end{aligned}$$

Proof

See Appendix 2. $\square$

The optimal consumption rule (12) implies that it is always optimal to consume more than the subsistence level. In fact, we have demonstrated in Appendix 2 that the ratio $\frac{R_{t}-H_{t}}{F_{t}}$ is always positive.

Here, the function $H_{t}$ measures the expected present value of all the future subsistence consumption ($c_{m}$) reduced by the expected present value of the future maximum, or potential, wage (i.e. the wage that the agent would receive if he supplied the maximum hours of labour L). This result implies that if $c_{m}$ is very high, then the optimal consumption will be close to this minimum level. In fact, if the consumption is sufficiently low, the wealth can be accumulated at a higher rate.

We note that the function $H_{t}$ can be simplified as follows

$$\begin{aligned} H_{t}&=c_{m}\int _{t}^{\infty }e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds-L{{\mathbb{E}}}_{t}^{{\mathbb{Q}}}\left[ \int _{t}^{\infty }\omega _{s}w_{s}e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] \\&=c_{m}\int _{t}^{\infty }e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds-L\Psi _{t}\left( T\right) , \end{aligned}$$

where only the second term depends on $w_{t}$, and actually coincides with the human capital defined in (7). We stress that $L\Psi _{t}\left( T\right)$ is the maximum human capital, i.e. the human capital that would be obtained by working the maximum number of available hours.

The first part of the function $H_{t}$ can be written as follows

$$\begin{aligned} A_{t}&:=c_{m}\int _{t}^{\infty }e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\\&=c_{m}{{\mathbb{E}}}_{t}\left[ \int _{t}^{\infty }e^{-r\left( s-t\right) }{{\mathbb{I}}}_{s<\Omega }ds\right] , \end{aligned}$$

which is the expected present value of a life annuity whose instalment is $c_{m}$.

Remark 2

The wealth that is taken into account for computing the optimal consumption, labour, and portfolio allocation is a kind of ‘modified’ wealth given by the nominal wealth $R_{t}$, reduced by the life annuity $A_{t}$, and increased by the human capital $L\Psi _{t}\left( T\right)$, i.e. $R_{t}-A_{t}+L\Psi _{t}\left( T\right)$. This means that the optimal behaviour of the agent is to buy a life annuity whose instalment is the minimum consumption $c_{m}$, and to borrow against his maximum human capital.

The optimal labour supply (13) is lower than the maximum level L. The optimal leisure, i.e. the difference $L-l_{t}^{*}$, is inversely proportional to the wage and directly proportional to the ratio $\frac{R_{t}-H_{t}}{F_{t}}$. Determining the sign of the elasticity of the labour supply with respect to $w_{t}$ is not trivial, since both function $H_{t}$ and $F_{t}$ depend on $w_{t}$. Nevertheless, by combining (12) and (13) we can write

$$\begin{aligned} L-l_{t}^{*}=\left( c_{t}^{*}-c_{m}\right) \left( \frac{\chi _{t}}{\omega _{t}w_{t}}\right) ^{\phi }, \end{aligned}$$

from which we obtain

$$\begin{aligned} \frac{\partial \left( L-l_{t}^{*}\right) }{\partial w_{t}}\frac{w_{t}}{\left( L-l_{t}^{*}\right) }=\frac{\partial \left( c_{t}^{*}-c_{m}\right) }{\partial w_{t}}\frac{w_{t}}{\left( c_{t}^{*}-c_{m}\right) }-\phi , \end{aligned}$$

where we can conclude what follows.

Corollary 3

The elasticity of the optimal leisure with respect to wage is always lower than the same elasticity of consumption.

Furthermore, we see that the exchange rate between labour and consumption is a function of the time preference $\phi$, while it does not depend on the risk aversion $\delta$.

The optimal portfolio (14) is formed by three components: (1) a speculative component $\frac{R_{t}-H_{t}}{\delta }\frac{\xi }{\sigma }$ which is proportional to the market price of risk $\xi$, and negatively depends on both the risk aversion $\delta$ and the volatility $\sigma$, (2) a hedging component that covers the agent against the stochastic changes in $H_{t}$ due to the changes in the wage $w_{t}$, and (3) a hedging component that covers against the stochastic changes in $F_{t}$ due to the changes in the wage $w_{t}$.

The function $F_{t}$ cannot be simplified further if we keep the hypothesis that $\phi \ne \frac{1}{\delta }$. Instead, if we merge the time preference and the risk aversion, the function $F_{t}$ takes the following linear form

$$\begin{aligned} F_{t}:={{\mathbb{E}}}_{t}^{{\mathbb{Q}}_{\delta }}\left[ \int _{t}^{\infty }\left( 1+\chi _{s}^{\frac{1}{\delta }}\left( \omega _{s}w_{s}\right) ^{1-\frac{1}{\delta }}\right) e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}\right) \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] , \end{aligned}$$

and can be further simplified as follows

$$\begin{aligned} F_{t}&={{\mathbb{E}}}_{t}^{{\mathbb{Q}}_{\delta }}\left[ {{\mathbb{I}}}_{t<T}\int _{t}^{T}\chi _{A}^{\frac{1}{\delta }}w_{s}e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}\right) \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] \\&\quad +{{\mathbb{E}}}_{t}^{{{\mathbb{Q}}}_{\delta }}\left[ {{\mathbb{I}}}_{t\ge T}\int _{T}^{\infty }\chi _{B}^{\frac{1}{\delta }}\omega w_{s}e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}\right) \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] \\&\quad +{{\mathbb{E}}}_{t}^{{{\mathbb{Q}}}_{\delta }}\left[ \int _{t}^{\infty }e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}\right) \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] . \end{aligned}$$

Accordingly, the optimal portfolio can be alternatively written as

$$\begin{aligned} S_{t}\theta _{t}^{*}&=\frac{R_{t}-H_{t}}{\delta }\frac{\xi }{\sigma }-\frac{w_{t}\sigma _{w}}{\sigma }L\frac{\partial \Psi _{t}\left( T\right) }{\partial w_{t}}\\&\quad +\frac{R_{t}-H_{t}}{F_{t}}\frac{w_{t}\sigma _{w}}{\sigma }\frac{\partial {{\mathbb{E}}}_{t}^{{{\mathbb{Q}}}_{\delta }}\left[ \int _{t}^{\infty }\chi _{s}^{\frac{1}{\delta }}\left( \omega _{s}w_{s}\right) ^{1-\frac{1}{\delta }}e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}\right) \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] }{\partial w_{t}}. \end{aligned}$$

The functions $H_{t}$ and $F_{t}$ contribute to the computation of the value function $J_{t}$ given in (17), as demonstrated in both Appendixes 1 and 2,

$$\begin{aligned} J_{t}=F_{t}^{\delta }\frac{\left( R_{t}-H_{t}\right) ^{1-\delta }}{1-\delta }. \end{aligned}$$

4 The optimal pension time problem

The optimal pension time can be found by solving the problem

$$\begin{aligned} \max _{T}J_{t_{0}}\left( \left. T\right| t_{0},w_{t_{0}},R_{t_{0}}\right) :=F_{t_{0}}^{\delta }\frac{\left( R_{t_{0}}-H_{t_{0}}\right) ^{1-\delta }}{1-\delta }, \end{aligned}$$

where the value function $J_{t}$ has been defined in (17).

Here, in order to obtain a result that can be computed in closed form, we restrict the analysis by assuming two simplifying hypotheses: (1) the force of mortality ($\lambda$) is constant, and (2) the time preference and risk preference are measured by the same parameter (i.e. $\phi =\frac{1}{\delta }$).

Under these hypotheses, the functions $H_{t}$ and $F_{t}$ contain the expected value of the wage $w_{t}$ under two probability measures. The process of $w_{t}$ under these probabilities is

$$\begin{aligned} \frac{dw_{t}}{w_{t}}&=\left( \mu _{w}-\xi \sigma _{w}\right) dt+\left( \sigma _{w}-\xi \right) dW_{t}^{{\mathbb{Q}}}\\&=\left( \mu _{w}-\frac{\delta -1}{\delta }\xi \sigma _{w}\right) dt+\sigma _{w}dW_{t}^{{{\mathbb{Q}}}_{\delta }}. \end{aligned}$$

Thus, the function $H_{t}$ can be written as⁶

$$\begin{aligned} H_{t}&=c_{m}\int _{t}^{\infty }e^{-\left( r+\lambda \right) \left( s-t\right) }ds-L{{\mathbb{E}}}_{t}^{{\mathbb{Q}}}\left[ \int _{t}^{\infty }\omega _{s}w_{s}e^{-\left( r+\lambda \right) \left( s-t\right) }ds\right] \\&=\frac{c_{m}}{r+\lambda }-L{{\mathbb{E}}}_{t}^{{\mathbb{Q}}}\left[ \int _{t}^{\infty }\left( {{\mathbb{I}}}_{s<T}+\omega \left( 1-{{\mathbb{I}}}_{s<T}\right) \right) w_{s}e^{-\left( r+\lambda \right) \left( s-t\right) }ds\right] \\&=\frac{c_{m}}{r+\lambda }-\frac{L\omega w_{t}}{r+\lambda -\left( \mu _{w}-\xi \sigma _{w}\right) }-L\left( 1-\omega \right) {{\mathbb{E}}}_{t}^{{\mathbb{Q}}}\left[ \int _{t}^{\infty }{{\mathbb{I}}}_{s<T}w_{s}e^{-\left( r+\lambda \right) \left( s-t\right) }ds\right] \end{aligned}$$

and so

$$\begin{aligned} H_{t}=\,&\frac{c_{m}}{r+\lambda }-\frac{L\omega w_{t}}{r+\lambda -\left( \mu _{w}-\xi \sigma _{w}\right) }\\&-L\left( 1-\omega \right) \times {\left\{ \begin{array}{ll} {{\mathbb{E}}}_{t}^{{\mathbb{Q}}}\left[ \int _{t}^{T}w_{s}e^{-\left( r+\lambda \right) \left( s-t\right) }ds\right] &{}\quad t<T\\ 0 &{}\quad t\ge T \end{array}\right. }. \end{aligned}$$

The function $F_{t}$, instead, has the following value:

$$\begin{aligned} F_{t}=\,&{{\mathbb{E}}}_{t}^{{{\mathbb{Q}}}_{\delta }}\left[ \int _{t}^{\infty }\left( 1+\chi _{s}^{\frac{1}{\delta }}\left( \omega _{s}w_{s}\right) ^{1-\frac{1}{\delta }}\right) e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda \right) \left( s-t\right) }ds\right] \\ =\,&\frac{1}{\frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda }\\&+{{\mathbb{E}}}_{t}^{{{\mathbb{Q}}}_{\delta }}\left[ \int _{t}^{\infty }\left( \chi _{A}^{\frac{1}{\delta }}w_{s}{{\mathbb{I}}}_{s<T}+\chi _{B}^{\frac{1}{\delta }}\omega w_{s}\left( 1-{{\mathbb{I}}}_{s<T}\right) \right) e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda \right) \left( s-t\right) }ds\right] \\ =\,&\frac{1}{\frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda }\\&+\chi _{B}^{\frac{1}{\delta }}\omega \int _{t}^{\infty }{{\mathbb{E}}}_{t}^{{{\mathbb{Q}}}_{\delta }}\left[ w_{s}\right] e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda \right) \left( s-t_{0}\right) }ds\\&+\left( \chi _{A}^{\frac{1}{\delta }}-\chi _{B}^{\frac{1}{\delta }}\omega \right) {{\mathbb{E}}}_{t}^{{{\mathbb{Q}}}_{\delta }}\left[ \int _{t}^{\infty }{{\mathbb{I}}}_{s<T}w_{s}e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda \right) \left( s-t_{0}\right) }ds\right] , \end{aligned}$$

and so we can write⁷

$$\begin{aligned} F_{t}&=\frac{1}{\frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda }\\&+\frac{\chi _{B}^{\frac{1}{\delta }}\omega w_{t}}{\frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda -\left( \mu _{w}-\frac{\delta -1}{\delta }\xi \sigma _{w}\right) }\\&+\left( \chi _{A}^{\frac{1}{\delta }}-\chi _{B}^{\frac{1}{\delta }}\omega \right) \times {\left\{ \begin{array}{ll} {{\mathbb{E}}}_{t}^{{{\mathbb{Q}}}_{\delta }}\left[ \int _{t}^{T}w_{s}e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda \right) \left( s-t_{0}\right) }ds\right] &{} t<T\\ 0 &{} t\ge T \end{array}\right. }. \end{aligned}$$

For solving both functions, we use the result of the following proposition.

Proposition 4

Given the stochastic process

$$\begin{aligned} \frac{dX_{t}}{X_{t}}=\alpha dt+\beta dW_{t}, \end{aligned}$$

and a stopping time T, with $X_{T}=x$, the following equations hold if $\rho >\alpha :$

$$\begin{aligned}&{{\mathbb{E}}}_{t_{0}}\left[ \int _{t_{0}}^{T}X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right] =\frac{X_{t_{0}}-x^{1-\gamma }X_{t_{0}}^{\gamma }}{\rho -\alpha },\\&{{\mathbb{E}}}_{t_{0}}\left[ \int _{T}^{\infty }X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right] =\frac{X_{t_{0}}}{\rho -\alpha }-{{\mathbb{E}}}_{t_{0}}\left[ \int _{t_{0}}^{T}X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right] =\frac{x^{1-\gamma }X_{t_{0}}^{\gamma }}{\rho -\alpha }, \end{aligned}$$

in which

$$\begin{aligned} \gamma :=-\left( \frac{\alpha }{\beta ^{2}}-\frac{1}{2}\right) +\sqrt{\left( \frac{\alpha }{\beta ^{2}}-\frac{1}{2}\right) ^{2}+\frac{2\rho }{\beta ^{2}}}. \end{aligned}$$

Proof

See Appendix 3. $\square$

Thanks to this result, we can finally compute the function $H_{t}$ as:

$$\begin{aligned} H_{t}=\frac{c_{m}}{r+\lambda }-\frac{L}{r+\lambda -\left( \mu _{w}-\xi \sigma _{w}\right) }\times {\left\{ \begin{array}{ll} w_{t}-\left( 1-\omega \right) \kappa ^{1-\gamma _{H}}w_{t}^{\gamma _{H}} &{} t<T\\ \omega w_{t} &{} t\ge T \end{array}\right. } \end{aligned}$$

in which

$$\begin{aligned} \gamma _{H}:=-\left( \frac{\mu _{w}-\xi \sigma _{w}}{\sigma _{w}^{2}}-\frac{1}{2}\right) +\sqrt{\left( \frac{\mu _{w}-\xi \sigma _{w}}{\sigma _{w}^{2}}-\frac{1}{2}\right) ^{2}+\frac{2\left( r+\lambda \right) }{\sigma _{w}^{2}}}. \end{aligned}$$

Remark 5

We stress that the shape of the function $H_{t}$ strongly depends on the value of $\omega$, which is the percentage of wage that is obtained if working is allowed after retirement. In fact,

• if $\omega >0$, the function $H_{t}$ after T is time dependent and is decreasing in $w_{t}$;

• if $\omega =0$ (i.e. working is not allowed after retirement), the function $H_{t}$ becomes constant after T and simply coincides with the discounted subsistence consumption level.

In the numerical simulations we will show the difference in the agent’s behaviour in these two cases.

The function $F_{t}$, instead, has the following value:

$$\begin{aligned} F_{t}=\,&\frac{1}{\frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda }+\frac{1}{\frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda -\left( \mu _{w}-\frac{\delta -1}{\delta }\xi \sigma _{w}\right) } \\&\times {\left\{ \begin{array}{ll} \chi _{A}^{\frac{1}{\delta }}w_{t}-\left( \chi _{A}^{\frac{1}{\delta }}-\chi _{B}^{\frac{1}{\delta }}\omega \right) \kappa ^{1-\gamma _{F}}w_{t}^{\gamma _{F}} &{} t<T\\ \chi _{B}^{\frac{1}{\delta }}\omega w_{t} &{} t\ge T \end{array}\right. } \end{aligned}$$

in which

$$\begin{aligned} \gamma _{F}:=-\left( \frac{\mu _{w}-\frac{\delta -1}{\delta }\xi \sigma _{w}}{\sigma _{w}^{2}}-\frac{1}{2}\right) +\sqrt{\left( \frac{\mu _{w}-\frac{\delta -1}{\delta }\xi \sigma _{w}}{\sigma _{w}^{2}}-\frac{1}{2}\right) ^{2}+2\frac{\frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{\delta }\frac{1}{2}\frac{\delta -1}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}+\lambda }{\sigma _{w}^{2}}}. \end{aligned}$$

Remark 6

Also the function $F_{t}$ has a shape that strongly depends on $\omega$. We see that when $\omega =0$ it becomes constant after T, while for $\omega >0$ it is increasing in $w_{t}$ also after T.

As it is common in the literature about optimal stopping time, we have now transformed the original optimal stopping problem into an optimal threshold problem where we want to find a value of the state variable (the wage) such that the value function is maximum. The optimal stopping time, then, is given by the first moment when the wage crosses the threshold.

Given the above results, the value function can be further simplified as follows, where $\kappa$ is the threshold of the wage (i.e. $\kappa :=w_{T}$):

$$\begin{aligned} J_{t_{0}}\left( \kappa \right) =F_{t_{0}}^{\delta }\frac{\left( R_{t_{0}}-H_{t_{0}}\right) ^{1-\delta }}{1-\delta } \end{aligned}$$

in which $H_{t_{0}}$ and $F_{t_{0}}$ are given by the above computed formulas.

5 The calibration of the model

5.1 The parameters

The parameters of the risky asset ($\mu$ and $\sigma$) are calibrated on the daily values of S&P500 from 1970 to 2018. We apply the method of moments to the geometric Brownian motion and we obtain

$$\begin{aligned} \mu =0.084,\quad \sigma =0.167. \end{aligned}$$

The wage process is calibrated on the wages and salaries for US workers (fred.stlouisfed.org series A576RC1A027NBEA) for the same period (1970–2018). The same method of moments gives

$$\begin{aligned} \mu _{w}=0.0612,\quad \sigma _{w}=0.07. \end{aligned}$$

The initial value of the wage is set to 20 dollars (per hour). Of course this value can be changed without any loss of generality, cause it affects just the level of the value function but not its shape.

The risk-less return is assumed to coincide with the average return on 3 month T-Bill from 1950 to 2018:

$$\begin{aligned} r=0.0437. \end{aligned}$$

For the sake of simplicity we further assume that the subjective discount rate $\rho$ coincides with this risk-less interest rate.

The force of mortality is calibrated on the data of the human mortality database (https://www.mortality.org/) for US, on the average of both males and females aged 25:

$$\begin{aligned} \lambda =0.0038. \end{aligned}$$

Here, we have used all annual data (interest rates and growth rates), and so the maximum number of working hours is set to $L=250\times 8$, given by the product between the number of working days in a year and the number of working hours in a day.

The initial wealth is set to a level that coincides with the total amount that could be received by working the maximum number of hours in a year at the initial wage (i.e. $Lw_{t_{0}}$).

The relative magnitude of $\chi _{A}$ and $\chi _{B}$ is crucial for determining the behaviour of the agent with respect to the working effort before and after retirement. Instead, the absolute magnitude of these two parameters is relevant for determining the optimal consumption.

We have conducted many simulations and we have checked that the values of $\chi _{A}$ and $\chi _{B}$ that generate optimal solutions that are consistent with the results usually obtained in the literature are

$$\begin{aligned} \chi _{A}=\frac{1}{10{,}000},\quad \chi _{B}=\frac{1.6}{10{,}000}. \end{aligned}$$

Furthermore, these values allow us to compare the magnitude of the leisure utility to the magnitude of the consumption utility (we recall that, under our previous hypotheses, the initial wealth is $R_{t_{0}}=w_{t_{0}}L=40{,}000$).

Finally, we will conduct two sets of simulations, one with $\omega =0$ for showing the agent’s behaviour when working is not allowed after retirement, and one with $\omega =\frac{1}{3}$ when the agent, after retirement, can obtain a salary that is one third of the salary received during his working life.

The values of all the parameters are gathered in Table 1.

Table 1 Parameters of the model

5.2 The value function and the optimal wage threshold

Fig. 1

Value function $J\left( \kappa \right)$ given the parameters shown in Table 1

The numerical values of the value function $J\left( \kappa \right)$, in which $\kappa$ is the wage threshold, are drawn in Fig. 1. The maximum of the function is obtained for

$$\begin{aligned} \kappa _{\omega =0}&=424.31,\\ \kappa _{\omega =1/3}&=170.68, \end{aligned}$$

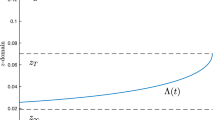
which are the thresholds of the wage above which the agent will decide to retire. If we simulate some trajectories of the wage and we compare them with these thresholds, we obtain the graph shown in Fig. 2.

Fig. 2

Optimal stopping time as the moment when the wage (simulated in light grey with 500 trajectories) goes above the (dotted) threshold $\kappa$ (in blue the case with $\omega =0$ and in red the case with $\omega =1/3$). In light grey the area between the 5 and 95 percentiles of the simulations

The time zero in the graph represents the first period when the agent starts receiving a wage. Thus, it should coincide with an age of about 25.

The main result is that, in our framework, it is optimal for an agent to retire depending on the wage that he will receive after retirement. In particular, we distinguish the following cases.

• If $\omega =0$ (no wage after retirement): it is optimal to retire after about 50 years of work (on average). We stress that the volatility of the wage in such a long period of time may imply an optimal retirement time that could be either anticipated to about 40 years of work or postponed up to more than 60 years.

• If $\omega =\frac{1}{3}$: it is optimal to retire after about 35 years of work (on average). In this case, the volatility of the forecast on the future wage may lead to a retirement either anticipated to less than 30 years of work, or postponed up to about 45 years.

If we compare this result with the EU15 average retirement age of 65 years and with the trend forecast for the next few years (towards 68 years for some states), we can identify a misalignment between the statutory and the optimal retirement age.

In our framework, we do not take into account any pension scheme and, thus, we do not have to comply with the related sustainability issue. Instead, in European public and private pension systems, such an issue is becoming more and more relevant over time, especially in the face of an ageing population and a reduced birth rate trend.

Another hypothesis for justifying this misalignment relates instead to the growth rate of wages. Indeed, if the wages increase at a lower rate, as shown, among others, by IMF (2018), European Commission (2018b) and Astrov et al. (2018), then it is optimal to retire later. A trend reduction in the average growth rate of wages could lead to an alignment between the statutory and the optimal retirement age.

5.3 The auxiliary functions

Under the hypotheses of our framework, the function $H_{t}$ is always negative (or zero) and we recall that it measures the (opposite of the) expected present value of the future wages (here we assume $c_{m}=0$). The value, over time, of this function is drawn in Fig. 3 for both cases $\omega \in \left\{ 0,\frac{1}{3}\right\}$.

We can see that with $\omega =0$ the function $H_{t}$ reaches an ‘equilibrium’ level and then becomes constant, while with $\omega =\frac{1}{3}$ it is monotonically decreasing over time.

Fig. 3

Average of 500 simulations of function $H_{t}$ over time (in blue the case with $\omega =0$ and in red the case with $\omega =1/3$)

The function $F_{t}$ is always strictly positive and its value, over time, is drawn in Fig. 4. Also in this case, we see a very different behaviour according to the value of $\omega$. If $\omega =0$ the function tends towards an equilibrium level, while for $\omega >0$ it is strictly increasing over time.

Fig. 4

Average of 500 simulations of function $F_{t}$ over time (in blue the case with $\omega =0$ and in red the case with $\omega =1/3$)

5.4 The optimal wealth, consumption, labour, and portfolio

Fig. 5

Average of 500 simulations of the optimal wealth $R_{t}^{*}$ (in blue the case with $\omega =0$ and in red the case with $\omega =1/3$)

In Fig. 5 we draw the optimal wealth. We check that the optimal wealth is increasing over time, but with $\omega =0$ its growth rate is much lower than with $\omega >0$. In fact, if the agent is allowed to have a wage even after retirement, he can obtain a higher growth rate of his wealth.

Fig. 6

Average of 500 simulations of the optimal labour supply $l_{t}^{*}$ (in blue the case with $\omega =0$ and in red the case with $\omega =1/3$)

In Fig. 6 we draw the optimal labour supply. We see that the average labour supply is decreasing over time, firstly at a higher speed, and for older ages at a lower speed. In this case the effect of $\omega$ is over the magnitude of the labour supply. In fact, if there is no more wage after retirement (i.e. $\omega =0$) the agent will work much more hours during his working life.

If $\omega =0$ the labour supply will fall to zero, while for $\omega >0$ it will become stable over time, at a very low level of about 100 working hour per year. The maximum number of working hours is about 700 per year, which may seem low. Such a result depends on two crucial hypotheses on financial market and agent’s preferences: (1) the market does not suffer any credit risk, in other words, the asset prices have some volatility, but they never go to zero, and the financial market is always able to fully recover from any fall, (2) the agent has a subsistence consumption $c_{m}=0$, which means that he is able to take utility even from a very low consumption.

In Fig. 6 we clearly see that after 60 years of work, the labour supply with $\omega =0$ sharply decreases. Of course, each of the simulated path will reach zero at a different time and, in fact, we see that the curve (which is the average of all the simulations) goes to zero after around 80 years.

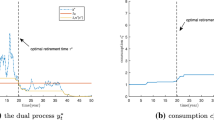
The optimal consumption of the agent can be expressed in different ways: (1) as a total amount of money spent, (2) as a percentage of the optimal wealth $R_{t}$, or (3) as a percentage of the disposable wealth $R_{t}-H_{t}$. This last way to represent consumption seems to be the best since it suitably takes into account the implicit hypothesis that the agent is able to borrow against his future wage. Figure 7 shows the average result of 500 simulations of the ratio $\frac{c_{t}^{*}}{R_{t}-H_{t}}$.

Fig. 7

Average of 500 simulations of the optimal consumption as a percentage of disposable wealth $\frac{c_{t}^{*}}{R_{t}-H_{t}}$ (in blue the case with $\omega =0$ and in red the case with $\omega =1/3$)

We see that when $\omega =0$ (no wage after retirement) the optimal (relative) consumption increases over time and once the retirement is reached, it becomes a constant percentage of the disposable wealth. The optimal consumption ratio starts from a value of about 2.5% and reaches, after retirement, its asymptotic value of about 5.5%. Instead, when $\omega >0$ the consumption rate is constantly decreasing as it happens in any infinite horizon optimisation problem. We recall that in this framework, the optimal consumption and the optimal labour supply are proportional. This means that when $\omega >0$, a lower labour supply is twinned with a lower consumption.

The optimal portfolio can be drawn, again, as a percentage of the disposable wealth $\frac{\theta _{t}^{*}}{R_{t}-H_{t}}$. The corresponding plot is shown in Fig. 8.

Fig. 8

Average of 500 simulations of the optimal portfolio as a percentage of disposable wealth $\frac{\theta _{t}^{*}}{R_{t}-H_{t}}$ (in blue the case with $\omega =0$ and in red the case with $\omega =1/3$)

We can see some interesting behaviours of the optimal portfolio share. Both portfolios, with $\omega =0$ and $\omega =\frac{1}{3}$ are on average increasing over time, nevertheless, the optimal portfolio for $\omega >0$ has a more stable growth from about $50\%$ to about 80%. This is a confirmation of the result often found in the literature: a young agent that still has to finance all his future consumption should invest less in the risky asset, while this percentage should increase while the agent becomes older and older.

The shape of the optimal portfolio for $\omega =0$, instead, presents some very interesting features.

• The percentage to invest in risky asset is almost always smaller (than in the case $\omega >0$): this is explained by the fact that with $\omega =0$ the agent cannot count on future wages after retirement and so his portfolio must be less aggressive.

• The portfolio is very volatile between 30 and 80 years of work, while it becomes constant after retirement. Actually, when both functions $F_{t}$ and $H_{t}$ become constant (after T), there is no more need for hedging against the wage volatility and the optimal portfolio becomes constant. When $\omega >0$, the need to hedge against the stochastic behaviour of $w_{t}$ remains almost unchanged over time, and so we find a smoother shape of the portfolio.

6 Conclusion

In our work we study the problem of a representative agent who wants to maximise the expected present value of his inter-temporal recursive utility by choosing the retirement age, the inter-temporal consumption, the labour supply, and the portfolio allocation.

If we assume that an agent starts working at about 25, our main results show that the optimal retirement age should be about 60 if the agent is still allowed to received a (reduced) wage after retirement, while it should be about 75 if working is not allowed after retirement. Comparing these results with the EU15 average retirement age (65 years), we find that this optimal retirement may be close to the optimal solution depending on the legislation about working after retirement.

A possible explanation for a misalignment between the statutory and the optimal solution is that, while first value is chosen to guarantee the financial sustainability of the pension system at macro level, the second derives from an optimal choice at the micro level.

All the results strongly rely on wage dynamics. In particular, if the wages increase at a lower rate, then it is optimal to retire later.

In our model the ratio between the optimal consumption and the disposable wealth increases over time from 2.5% to about 5.5% and, after retirement, it remains constant over time if the pensioner is not allowed to work. On the contrary, the optimal consumption is a constantly reducing percentage of wealth. Moreover, we find that the percentage of disposable wealth invested in the risky asset is smoothly increasing over time if pensioners are allowed to work, while this percentage becomes constant after retirement if this is not allowed.

Appendices

Appendix 1: Proof of Proposition 1

Given the agent’s preferences, the value function $J_{t}\left( R_{t},w_{t}\right)$ solving the agent’s maximisation problem, must satisfy the Hamilton Jacobi Bellman (HJB) partial differential equation defined as follows⁸

$$\begin{aligned} 0&=\partial _{t}^{J}-\left( \rho +\lambda _{t}\right) \frac{1-\delta }{1-\frac{1}{\phi }}J_{t}+\partial _{R}^{J}R_{t}\left( r+\lambda _{t}\right) \\&\quad +\partial _{w}^{J}w_{t}\mu _{w}+\frac{1}{2}\partial _{ww}^{J}\left( w_{t}\sigma _{w}\right) ^{2}\\&\quad +\max _{c_{t}}\left[ \frac{\left( c_{t}-c_{m}\right) ^{1-\frac{1}{\phi }}}{1-\frac{1}{\phi }}\left( \left( 1-\delta \right) J_{t}\right) ^{1-\frac{1-\frac{1}{\phi }}{1-\delta }}-\partial _{R}^{J}c_{t}\right] \\&\quad +\max _{l_{t}}\left[ \chi _{t}\frac{\left( L-l_{t}\right) ^{1-\frac{1}{\phi }}}{1-\frac{1}{\phi }}\left( \left( 1-\delta \right) J_{t}\right) ^{1-\frac{1-\frac{1}{\phi }}{1-\delta }}+\partial _{R}^{J}\omega _{t}w_{t}l_{t}\right] \\&\quad +\max _{\theta _{t}}\left[ \partial _{R}^{J}\theta _{t}S_{t}\left( \mu -r\right) +\frac{1}{2}\partial _{RR}^{J}\left( \theta _{t}S_{t}\sigma \right) ^{2}+\partial _{wR}^{J}\theta _{t}S_{t}\sigma w_{t}\sigma _{w}\right] , \end{aligned}$$

with transversality condition

$$\begin{aligned} \lim _{t\rightarrow \infty }J_{t}e^{-\int _{t_{0}}^{t}\rho +\lambda _{s}ds}=0. \end{aligned}$$

The First Order Condition (FOC) on consumption $c_{t}$ is

$$\begin{aligned} c_{t}^{*}=c_{m}+\left( \partial _{R}^{J}\right) ^{-\phi }\left( \left( 1-\delta \right) J_{t}\right) ^{\phi +\frac{1-\phi }{1-\delta }}, \end{aligned}$$

the FOC on labour $l_{t}$ is

$$\begin{aligned} l_{t}^{*}=L-\left( \partial _{R}^{J}\frac{\omega _{t}w_{t}}{\chi _{t}}\right) ^{-\phi }\left( \left( 1-\delta \right) J_{t}\right) ^{\phi +\frac{1-\phi }{1-\delta }}, \end{aligned}$$

and the FOC on portfolio $\theta _{t}$ is

$$\begin{aligned} \theta _{t}^{*}S_{t}=-\frac{\partial _{R}^{J}}{\partial _{RR}^{J}}\frac{\mu -r}{\sigma ^{2}}-\frac{\partial _{wR}^{J}}{\partial _{RR}^{J}}w_{t}\frac{\sigma _{w}}{\sigma }. \end{aligned}$$

Once these candidates to the optimal are substituted into the HJB equation we get

$$\begin{aligned} 0&=\partial _{t}^{J}-\left( \rho +\lambda _{t}\right) \frac{1-\delta }{1-\frac{1}{\phi }}J_{t}+\partial _{R}^{J}R_{t}\left( r+\lambda _{t}\right) +\partial _{R}^{J}\omega _{t}w_{t}L-\partial _{R}^{J}c_{m}\\&\quad +\partial _{w}^{J}w_{t}\mu _{w}+\frac{1}{2}\partial _{ww}^{J}\left( w_{t}\sigma _{w}\right) ^{2}\\&\quad +\frac{1}{\phi -1}\left( 1+\chi _{t}\left( \frac{\omega _{t}w_{t}}{\chi _{t}}\right) ^{1-\phi }\right) \left( \left( 1-\delta \right) J_{t}\right) ^{\phi +\frac{1-\phi }{1-\delta }}\left( \partial _{R}^{J}\right) ^{1-\phi }\\&\quad -\frac{1}{2}\frac{\left( \partial _{R}^{J}\right) ^{2}}{\partial _{RR}^{J}}\left( \frac{\mu -r}{\sigma }\right) ^{2}-\frac{\partial _{R}^{J}\partial _{wR}^{J}}{\partial _{RR}^{J}}w_{t}\frac{\sigma _{w}}{\sigma }\left( \mu -r\right) -\frac{1}{2}\frac{\left( \partial _{wR}^{J}\right) ^{2}}{\partial _{RR}^{J}}\left( w_{t}\sigma _{w}\right) ^{2}. \end{aligned}$$

In order to solve this PDE we guess the following solution

$$\begin{aligned} J_{t}=F_{t}^{\delta }\frac{\left( R_{t}-H_{t}\right) ^{1-\delta }}{1-\delta }, \end{aligned}$$

(17)

in which $H_{t}\left( t,w_{t}\right)$ and $F_{t}\left( t,w_{t}\right)$ are two functions whose values must solve the HJB equation.

If we substitute this function into the HJB we get a PDE that can be split into two PDEs, one that contains the terms $\left( R_{t}-H_{t}\right) ^{1-\delta }$:

$$\begin{aligned} 0=\,&\delta F_{t}^{\delta -1}\frac{\left( R_{t}-H_{t}\right) ^{1-\delta }}{1-\delta }\partial _{t}^{F}+F_{t}^{\delta -1}\left( R_{t}-H_{t}\right) ^{1-\delta }w_{t}\frac{\delta }{1-\delta }\left( \mu _{w}+\frac{1-\delta }{\delta }\sigma _{w}\frac{\mu -r}{\sigma }\right) \partial _{w}^{F}\\&+\frac{1}{2}\left( w_{t}\sigma _{w}\right) ^{2}\delta F_{t}^{\delta -1}\frac{\left( R_{t}-H_{t}\right) ^{1-\delta }}{1-\delta }\partial _{ww}^{F}\nonumber \\&-\left( \rho +\lambda _{t}\right) \frac{1-\delta }{1-\frac{1}{\phi }}F_{t}^{\delta }\frac{\left( R_{t}-H_{t}\right) ^{1-\delta }}{1-\delta }+F_{t}^{\delta }\left( R_{t}-H_{t}\right) ^{1-\delta }\left( r+\lambda _{t}\right) \nonumber \\&+\frac{1}{2}F_{t}^{\delta }\frac{\left( R_{t}-H_{t}\right) ^{1-\delta }}{\delta }\left( \frac{\mu -r}{\sigma }\right) ^{2}\nonumber \\&+\frac{1}{\phi -1}\left( 1+\chi _{t}^{\phi }\left( \omega _{t}w_{t}\right) ^{1-\phi }\right) F_{t}^{\delta \left( 1+\frac{1-\phi }{1-\delta }\right) }\left( R_{t}-H_{t}\right) ^{1-\delta },\nonumber \end{aligned}$$

(18)

and one that contains the terms $\left( R_{t}-H_{t}\right) ^{-\delta }$

$$\begin{aligned} 0=\,&-F_{t}^{\delta }\left( R_{t}-H_{t}\right) ^{-\delta }\partial _{t}^{H}-F_{t}^{\delta }\left( R_{t}-H_{t}\right) ^{-\delta }w_{t}\left( \mu _{w}-\sigma _{w}\frac{\mu -r}{\sigma }\right) \partial _{w}^{H}\\&-\frac{1}{2}\left( w_{t}\sigma _{w}\right) ^{2}F_{t}^{\delta }\left( R_{t}-H_{t}\right) ^{-\delta }\partial _{ww}^{H}\nonumber \\&+F^{\delta }\left( R_{t}-H_{t}\right) ^{-\delta }H_{t}\left( r+\lambda _{t}\right) +F_{t}^{\delta }\left( R_{t}-H_{t}\right) ^{-\delta }\left( \omega _{t}w_{t}L-c_{m}\right) .\nonumber \end{aligned}$$

(19)

These two equations can be simplified as follows

$$\begin{aligned} 0=\,&\partial _{t}^{F}+w_{t}\left( \mu _{w}-\frac{\delta -1}{\delta }\sigma _{w}\frac{\mu -r}{\sigma }\right) \partial _{w}^{F}+\frac{1}{2}\left( w_{t}\sigma _{w}\right) ^{2}\partial _{ww}^{F} \end{aligned}$$

(20)

$$\begin{aligned}&-\frac{\delta -1}{\delta }F_{t}\left( \left( \rho +\lambda _{t}\right) \frac{1}{\frac{1}{\phi }-1}+\left( r+\lambda _{t}\right) +\frac{1}{\delta }\frac{1}{2}\left( \frac{\mu -r}{\sigma }\right) ^{2}\right) \nonumber \\&+\frac{1}{\phi -1}\frac{1-\delta }{\delta }\left( 1+\chi _{t}^{\phi }\left( \omega _{t}w_{t}\right) ^{1-\phi }\right) F_{t}^{1+\delta \frac{1-\phi }{1-\delta }},\nonumber \\ 0=\,&\partial _{t}^{H}+w_{t}\left( \mu _{w}-\sigma _{w}\frac{\mu -r}{\sigma }\right) \partial _{w}^{H}+\frac{1}{2}\left( w_{t}\sigma _{w}\right) ^{2}\partial _{ww}^{H}\\&-\left( H_{t}\left( r+\lambda _{t}\right) +\omega _{t}w_{t}L-c_{m}\right) .\nonumber \end{aligned}$$

(21)

If we use the Feynman-Kac solution of these equations (see Yong and Zhou 1999; Øksendal 2000; Björk 2009), together with the transversality condition, we get the functions defined in the proposition.

Instead of proving the verification theorem, in Appendix 2 we demonstrate the same result with the so called ‘martingale approach’ due to Cox and Huang (1989). The demonstration is based on the case that we will use for the computation of the optimal stopping time, i.e. the case when the risk preference and the time preference are measure by the same parameter ($\phi =\frac{1}{\delta }$).

Appendix 2: Alternative proof of Proposition 1

In solving the first step of Problem (11), we neglect the last term containing only the choice variable T. Here, we take into account the linear case with $\phi =\frac{1}{\delta }$. The Lagrangian of the problem is

$$\begin{aligned} \mathcal {L}:=\,&{{\mathbb{E}}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }\left( \frac{\left( c_{s}-c_{m}\right) ^{1-\delta }}{1-\delta }+\chi _{A}\frac{\left( L-l_{s}\right) ^{1-\delta }}{1-\delta }{{\mathbb{I}}}_{s<T}\right) e^{-\rho \left( s-t_{0}\right) -\int _{t_{0}}^{s}\lambda _{u}du}ds\right] \\&+\phi \left( R_{t_{0}}+{\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }\left( l_{s}w_{s}{\mathbb{I}}_{s<T}-c_{s}\right) m_{t_{0},s}e^{-r\left( s-t_{0}\right) -\int _{0}^{s}\lambda _{u}du}ds\right] \right) , \end{aligned}$$

where $\phi$ is the (constant) Lagrangian multiplier. The F.O.C. on consumption for any time s is:

$$\begin{aligned} \left( c_{s}-c_{m}\right) ^{-\delta }e^{-\rho \left( s-t_{0}\right) -\int _{t_{0}}^{s}\lambda _{u}du}-\phi m_{t_{0},s}e^{-r\left( s-t_{0}\right) -\int _{t_{0}}^{s}\lambda _{u}du}=0, \end{aligned}$$

from which

$$\begin{aligned} c_{s}^{*}=c_{m}+\left( \phi m_{t_{0},s}\frac{e^{-r\left( s-t_{0}\right) }}{e^{-\rho \left( s-t_{0}\right) }}\right) ^{-\frac{1}{\delta }}, \end{aligned}$$

while the F.O.C. on labour for any time s is:

$$\begin{aligned} l_{s}^{*}=L-\left( \phi \frac{w_{s}}{\chi _{A}}m_{t_{0},s}\frac{e^{-\left( s-t_{0}\right) r}}{e^{-\rho \left( s-t_{0}\right) }}\right) ^{-\frac{1}{\delta }}. \end{aligned}$$

Once $c_{s}^{*}$ and $l_{s}^{*}$ are substituted into the constraint, rewritten at any time t, we have

$$\begin{aligned} R_{t}+{\mathbb{E}}_{t}\left[ \int _{t}^{\infty }\left( l_{s}^{*}w_{s}{\mathbb{I}}_{s<T}-c_{s}^{*}\right) m_{t,s}e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] =0, \end{aligned}$$

or

$$\begin{aligned} 0&=R_{t}-{\mathbb{E}}_{t}\left[ \int _{t}^{\infty }\left( c_{m}-Lw_{s}{\mathbb{I}}_{s<T}\right) m_{t,s}e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] \\&\quad -\phi ^{-\frac{1}{\delta }}{\mathbb{E}}_{t}\left[ \int _{t}^{\infty }\left( \chi _{A}^{\frac{1}{\delta }}w_{s}^{1-\frac{1}{\delta }}{\mathbb{I}}_{s<T}+1\right) \left( m_{t_{0},s}\frac{e^{-r\left( s-t_{0}\right) }}{e^{-\rho \left( s-t_{0}\right) }}\right) ^{-\frac{1}{\delta }}m_{t,s}e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] . \end{aligned}$$

Now we use the property of the price kernel $m_{t_{0},s}=m_{t_{0},t}m_{t,s}$ for all $t_{0}\le t\le s$ and we write

$$\begin{aligned} \left( m_{t_{0},s}\frac{e^{-r\left( s-t_{0}\right) }}{e^{-\rho \left( s-t_{0}\right) }}\right) ^{-\frac{1}{\delta }}=\left( m_{t_{0},t}\frac{e^{-r\left( t-t_{0}\right) }}{e^{-\rho \left( t-t_{0}\right) }}m_{t,s}\frac{e^{-r\left( s-t\right) }}{e^{-\rho \left( s-t\right) }}\right) ^{-\frac{1}{\delta }}, \end{aligned}$$

so that the previous equation can be simplified as follows

$$\begin{aligned} 0&=R_{t}-{\mathbb{E}}_{t}\left[ \int _{t}^{\infty }\left( c_{m}-Lw_{s}{\mathbb{I}}_{s<T}\right) m_{t,s}e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] \\&\quad -\phi ^{-\frac{1}{\delta }}\left( m_{t_{0},t}\frac{e^{-r\left( t-t_{0}\right) }}{e^{-\rho \left( t-t_{0}\right) }}\right) ^{-\frac{1}{\delta }}{\mathbb{E}}_{t}\left[ \int _{t}^{\infty }\left( \chi _{A}^{\frac{1}{\delta }}w_{s}^{1-\frac{1}{\delta }}{\mathbb{I}}_{s<T}+1\right) m_{t,s}^{1-\frac{1}{\delta }}e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho \right) \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] . \end{aligned}$$

The power $m_{t,s}^{1-\frac{1}{\delta }}$ is not a martingale, and, accordingly, we cannot use it for change the probability. Nevertheless, the process $m_{t,s}^{1-\frac{1}{\delta }}e^{\frac{1}{2}\frac{1}{\delta }\frac{\delta -1}{\delta }\xi ^{2}\left( s-t\right) }$ is a martingale. In fact, given the dynamics (4) we have

$$\begin{aligned} \frac{d\left( m_{t,s}^{1-\frac{1}{\delta }}e^{\frac{1}{2}\frac{1}{\delta }\frac{\delta -1}{\delta }\xi ^{2}\left( s-t\right) }\right) }{m_{t,s}^{1-\frac{1}{\delta }}e^{\frac{1}{2}\frac{1}{\delta }\frac{\delta -1}{\delta }\xi ^{2}\left( s-t\right) }}=-\frac{\delta -1}{\delta }\xi dW_{t}. \end{aligned}$$

Accordingly, we can use Girsanov’s theorem for defining a new probability ${\mathbb{Q}}_{\delta }$ such that

$$\begin{aligned} dW_{t}^{{\mathbb{Q}}_{\delta }}=\frac{\delta -1}{\delta }\xi dt+dW_{t}. \end{aligned}$$

Finally, for simplifying the notation we can define the following functions:

$$\begin{aligned}&H_{t}:={\mathbb{E}}_{t}^{{\mathbb{Q}}}\left[ \int _{t}^{\infty }\left( c_{m}-Lw_{s}{\mathbb{I}}_{s<T}\right) e^{-r\left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] ,\\&F_{t}:={\mathbb{E}}_{t}^{{\mathbb{Q}}_{\delta }}\left[ \int _{t}^{\infty }\left( \chi _{A}^{\frac{1}{\delta }}w_{s}^{1-\frac{1}{\delta }}{\mathbb{I}}_{s<T}+1\right) e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho +\frac{1}{2}\frac{1}{\delta }\frac{\delta -1}{\delta }\xi ^{2}\right) \left( s-t\right) -\int _{t}^{s}\lambda _{u}du}ds\right] , \end{aligned}$$

and so

$$\begin{aligned} R_{t}=H_{t}+\phi ^{-\frac{1}{\delta }}m_{t_{0},t}^{-\frac{1}{\delta }}\left( \frac{e^{-r\left( t-t_{0}\right) }}{e^{-\rho \left( t-t_{0}\right) }}\right) ^{-\frac{1}{\delta }}F_{t}. \end{aligned}$$

(22)

The value of the Lagrangian multiplier must be found in such a way that it satisfies the constraint:

$$\begin{aligned} R_{t_{0}}=\,&{\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }\left( c_{s}^{*}-l_{s}^{*}w_{s}{\mathbb{I}}_{s<T}\right) m_{t_{0},s}e^{-r\left( s-t_{0}\right) -\int _{t_{0}}^{s}\lambda _{u}du}ds\right] \\ =\,&{\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }\left( c_{m}-Lw_{s}{\mathbb{I}}_{s<T}\right) m_{t_{0},s}e^{-r\left( s-t_{0}\right) -\int _{t_{0}}^{s}\lambda _{u}du}ds\right] \\&+\phi ^{-\frac{1}{\delta }}{\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }m_{t_{0},s}^{1-\frac{1}{\delta }}\left( 1+\chi _{A}^{\frac{1}{\delta }}w_{s}^{1-\frac{1}{\delta }}{\mathbb{I}}_{s<T}\right) e^{-\left( \frac{\delta -1}{\delta }r+\frac{1}{\delta }\rho \right) \left( s-t_{0}\right) -\int _{t_{0}}^{s}\lambda _{u}du}ds\right] . \end{aligned}$$

Thus, we see that

$$\begin{aligned} R_{t_{0}}=H_{t_{0}}+\phi ^{-\frac{1}{\delta }}F_{t}, \end{aligned}$$

from which

$$\begin{aligned} \phi =\left( \frac{R_{t_{0}}-H_{t_{0}}}{F_{t_{0}}}\right) ^{-\delta }. \end{aligned}$$

This means that (22) can be written as a function of the initial wealth as follows:

$$\begin{aligned} \frac{R_{t}-H_{t}}{F_{t}}=\frac{R_{t_{0}}-H_{t_{0}}}{F_{t_{0}}}m_{t_{0},t}^{-\frac{1}{\delta }}\left( \frac{e^{-r\left( t-t_{0}\right) }}{e^{-\rho \left( t-t_{0}\right) }}\right) ^{-\frac{1}{\delta }}. \end{aligned}$$

Given the stochastic differential equations for the wage (5) and for the price kernel (4), the differential of $R_{t}$ is

$$\begin{aligned} dR_{t}=\,&\left( ...\right) dt+\left( \frac{\partial H_{t}}{\partial w_{t}}+\phi ^{-\frac{1}{\delta }}m_{t_{0},t}^{-\frac{1}{\delta }}\left( \frac{e^{-r\left( t-t_{0}\right) }}{e^{-\left( t-t_{0}\right) \rho }}\right) ^{-\frac{1}{\delta }}\frac{\partial F_{t}}{\partial w_{t}}\right) w_{t}\sigma _{w}dW_{t}\\&-\left( -\frac{1}{\delta }\phi ^{-\frac{1}{\delta }}m_{t_{0},t}^{-\frac{1}{\delta }-1}\left( \frac{e^{-r\left( t-t_{0}\right) }}{e^{-\left( t-t_{0}\right) \rho }}\right) ^{-\frac{1}{\delta }}F_{t}\right) m_{t_{0},t}\xi dW_{t}, \end{aligned}$$

and, since

$$\begin{aligned} \frac{R_{t}-H_{t}}{F_{t}}=\phi ^{-\frac{1}{\delta }}m_{t_{0},t}^{-\frac{1}{\delta }}\left( \frac{e^{-r\left( t-t_{0}\right) }}{e^{-\left( t-t_{0}\right) \rho }}\right) ^{-\frac{1}{\delta }}, \end{aligned}$$

it becomes

$$\begin{aligned} dR_{t}=\left( ...\right) dt+\left( \frac{\partial H_{t}}{\partial w_{t}}+\frac{R_{t}-H_{t}}{F_{t}}\frac{\partial F_{t}}{\partial w_{t}}\right) w_{t}\sigma _{w}dW_{t}+\frac{R_{t}-H_{t}}{\delta }\xi dW_{t}. \end{aligned}$$

The optimal portfolio is then

$$\begin{aligned} S_{t}\theta _{t}^{*}=\frac{R_{t}-H_{t}}{\delta }\frac{\xi }{\sigma }+\frac{w_{t}\sigma _{w}}{\sigma }\left( \frac{\partial H_{t}}{\partial w_{t}}+\frac{R_{t}-H_{t}}{F_{t}}\frac{\partial F_{t}}{\partial w_{t}}\right) , \end{aligned}$$

while the optimal consumption and labour are those presented in the proposition.

Appendix 3: Proof of Proposition 4

Given a geometric Brownian motion

$$\begin{aligned} \frac{dX_{t}}{X_{t}}=\alpha dt+\beta dW_{t}, \end{aligned}$$

whose solution is (with $W_{t_{0}}=0$)

$$\begin{aligned} X_{t}=X_{t_{0}}e^{\left( \alpha -\frac{1}{2}\beta ^{2}\right) \left( t-t_{0}\right) +\beta W_{t}}, \end{aligned}$$

we want to compute the expected value ${\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{T}X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right]$ that can be simplified as follows

$$\begin{aligned}&{\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{T}X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right] \\ \quad =\,&{\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }X_{s}e^{-\rho \left( s-t_{0}\right) }ds-\int _{T}^{\infty }X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right] \\\quad =\,&{\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{\infty }X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right] -{\mathbb{E}}_{t_{0}}\left[ \int _{T}^{\infty }X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right] \\\quad =\,&\int _{t_{0}}^{\infty }{\mathbb{E}}_{t_{0}}\left[ X_{s}\right] e^{-\rho \left( s-t_{0}\right) }ds-{\mathbb{E}}_{t_{0}}\left[ e^{-\rho T}\int _{T}^{\infty }X_{s}e^{-\rho \left( s-T\right) }ds\right] \\\quad =\,&\int _{t_{0}}^{\infty }X_{t_{0}}e^{-\left( \rho -\alpha \right) \left( s-t_{0}\right) }ds-{\mathbb{E}}_{t_{0}}\left[ e^{-\rho T}\int _{T}^{\infty }{\mathbb{E}}_{T}\left[ X_{s}\right] e^{-\rho \left( s-T\right) }ds\right] \\\quad =\,&\frac{X_{t_{0}}}{\rho -\alpha }-{\mathbb{E}}_{t_{0}}\left[ e^{-\rho T}X_{T}\int _{T}^{\infty }e^{-\left( \rho -\alpha \right) \left( s-T\right) }ds\right] \\\quad =\,&\frac{X_{t_{0}}}{\rho -\alpha }-{\mathbb{E}}_{t_{0}}\left[ e^{-\rho T}\frac{X_{T}}{\rho -\alpha }\right] \\\quad =\,&\frac{X_{t_{0}}-{\mathbb{E}}_{t_{0}}\left[ X_{T}e^{-\rho T}\right] }{\rho -\alpha }. \end{aligned}$$

Then, it is now sufficient to compute the remaining expected value ${\mathbb{E}}_{t_{0}}\left[ X_{T}e^{-\rho T}\right]$. If we call x the value of the process at the stopping time T (i.e. $x=X_{T}$), then

$$\begin{aligned} {\mathbb{E}}_{t_{0}}\left[ X_{T}e^{-\rho T}\right] =x^{1-\gamma }X_{t_{0}}^{\gamma }, \end{aligned}$$

where

$$\begin{aligned} \gamma =\frac{1}{2}-\frac{\mu }{\sigma ^{2}}+\sqrt{\left( \frac{1}{2}-\frac{\mu }{\sigma ^{2}}\right) ^{2}+2\frac{\rho }{\sigma ^{2}}}. \end{aligned}$$

Finally, we can write

$$\begin{aligned} {\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{T}X_{s}e^{-\rho \left( s-t_{0}\right) }ds\right] =\frac{X_{t_{0}}-x^{1-\gamma }X_{t_{0}}^{\gamma }}{\rho -\alpha }. \end{aligned}$$

These same results allow us to write also

$$\begin{aligned} {\mathbb{E}}_{t_{0}}\left[ \int _{t_{0}}^{T}e^{-\rho \left( s-t_{0}\right) }ds\right] =\frac{1-{\mathbb{E}}_{t_{0}}\left[ e^{-\rho T}\right] }{\rho }=\frac{1-x^{-\gamma }X_{t_{0}}^{\gamma }}{\rho }. \end{aligned}$$