Firms’ strategic delegation with heterogeneous consumers

Abstract

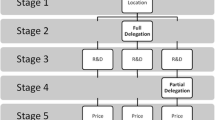
We revisit firms’ strategic delegation in a Cournot game. We consider a market comprising two consumer groups, with either a high or low willingness to pay. In this market, we first consider firms’ identical marginal costs and show that either/both firms’ owners may strategically abandon the delegation option to avoid price collapse. We find three types of delegation decisions with either/both/no firm delegating in equilibrium. We further consider firms’ asymmetric marginal costs and show that the asymmetric equilibrium wherein only the less efficient firm delegates will exist in a wider parameter range, compared to that wherein only the more efficient firm delegates. Moreover, delegation may enable the less efficient firm to achieve a higher profit than her rival.

Appendix

1.1 Proof of Lemma 1:

By maximizing $O^k_i$ based on the inverse demand function in Eq. (1), manager i’s reaction function as follows:

$$\begin{aligned} R_{i}(q_{j}) = \left\{ \begin{array}{ll} \displaystyle R^{S}(q_j)&{} if \ q_{i}+q_{j}\le 1-a, \\ \displaystyle R^{I}(q_j) &{} if \ q_{i}+q_{j}>1-a. \end{array} \right. \end{aligned}$$

(14)

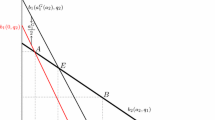
The existence of a market separation needs to satisfy $R^{S}(q_{j})+q_j\le 1-a$, which gives rise to

$$\begin{aligned} \displaystyle q_j\le 1+\theta _ic_i-2a. \end{aligned}$$

(15)

The existence of a market integration needs to satisfy $R^{I}(q_j)+q_j>1-a$, which gives rise to

$$\begin{aligned} \displaystyle q_j\,>\,\frac{1+a}{a}\theta _ic_i-2a. \end{aligned}$$

(16)

For $(1+a)\theta _ic_i/a-2a<q_j\le 1+\theta _ic_i-2a$, the manager i chooses $R^{S}(q_j)$ if $O_i^{S}[q_j,R^{S}(q_j)]\ge O_i^{I}[q_j,R^{I}(q_j)]$ from which

$$\begin{aligned} q_{j}\le {\bar{q}}_j. \end{aligned}$$

(17)

Because $(1+a)\theta _ic_i/a-2a<{\bar{q}}_j\le 1+\theta _ic_i-2a$ for any feasible a, $c_i$ and $\theta _i$, Firm i chooses $R^{S}(q_j)$ for $q_j\le {\bar{q}}_j$. Thus, we obtain the reaction function as in Eq. (6).

1.2 Proof of Lemma 2, 3 and 4:

Substituting ${\varvec{\theta }}^{nnS}$, ${\varvec{\theta }}^{nnI}$, ${\varvec{\theta }}^{dnS}$, ${\varvec{\theta }}^{dnI}$ , ${\varvec{\theta }}^{ddS}$, ${\varvec{\theta }}^{ddI}$ to Eq. (6), we can derive the threshold values of ${\bar{q}}_j$ that define each firm’s discontinuous reaction function. Substituting these incentive rates to Eq. (7), we can obtain firms’ equilibrium quantities. By further substituting the equilibrium quantities to Eq. (2), we can obtain firms’ equilibrium profits. The equilibrium values are summarized in Table 1.

Table 1 Equilibrium outcomes with $Z\equiv (a+1)/a$

To prove the first part of Lemma 2, we let $q_1^{nnS}\le {\bar{q}}_1^{nnS}$ (or $q_2^{nnS}\le {\bar{q}}_2^{nnS}$), from which we have

$$\begin{aligned} c\ge {\tilde{c}}^{nnS}\equiv \frac{11 a + 6 a^2- 6(a-a^2)\sqrt{Z} }{9 + 8 a}. \end{aligned}$$

Notice that ${\tilde{c}}^{nnS}>0$ if and only if $a>4/21$, which is part (ii) of Assumption 1.

To prove the second part of Lemma 2, we let $q_1^{nnI}\ge {\bar{q}}_1^{nnI}$ (or $q_2^{nnI}\ge {\bar{q}}_2^{nnI}$), from which we have

$$\begin{aligned} c\le {\tilde{c}}^{nnI}\equiv \frac{a + 6 a^2-6(a - a^2 )\sqrt{1/Z}}{ 8 a-1}. \end{aligned}$$

To prove the first part of Lemma 3, we let $q_1^{dnS}\le {\bar{q}}_1^{dnS}$ and $q_2^{dnS}\le {\bar{q}}_2^{dnS}$, from which we have

$$\begin{aligned} c\ge \frac{5a+2a^2-2(a-a^2)\sqrt{Z}}{4+3a}\ and\ c\ge {\tilde{c}}^{dnS}\equiv \frac{5 + 28 a + 16 a^2-16(a-a^2)\sqrt{Z}}{25 + 24 a}. \end{aligned}$$

Under Assumption 1, the second inequality is a sufficient condition for the first one. To prove the second part of Lemma 3, we let $q_1^{dnI}\ge {\bar{q}}_1^{dnI}$ and $q_2^{dnI}\ge {\bar{q}}_2^{dnI}$, from which we have

$$\begin{aligned} c\le \frac{2(a^2 + a^2\sqrt{Z} )}{1 + a + 2a\sqrt{Z}}\ and\ c\le {\tilde{c}}^{dnI}\equiv \displaystyle \frac{2a + 28 a^2 + 16 a^3-16a( 1-a^2)\sqrt{1/Z } }{(1 + a) ( 24 a-1)}. \end{aligned}$$

Under Assumption 1, the second inequality is a sufficient condition for the first one.

To prove the first part of Lemma 4, we let $q_1^{ddS}\le {\bar{q}}_1^{ddS}$ (or $q_2^{ddS}\le {\bar{q}}_2^{ddS}$), from which we have

$$\begin{aligned} c\ge {\tilde{c}}^{ddS}\equiv \frac{3 + 21 a + 10 a^2 -10(a-a^2)\sqrt{Z}}{2 (9 + 8 a)}. \end{aligned}$$

To prove the second part of Lemma 4, we let $q_1^{ddI}\ge {\bar{q}}_1^{ddI}$ (or $q_2^{ddI}\ge {\bar{q}}_2^{ddI}$), from which we have

$$\begin{aligned} c\le {\tilde{c}}^{ddI}\equiv \displaystyle \frac{a + 17 a^2 + 10 a^3-10a(1-a^2)\sqrt{1/Z}}{2 (1 + a) ( 8 a-1)}. \end{aligned}$$

1.3 Proof of Proposition 1

Firms’ equilibrium profits are summarized in Table 1. To guarantee the existence of the asymmetric equilibria (case dn), we let $a>0.734$ (Remark 2). Then, we have ${\tilde{c}}^{nnI}<{\tilde{c}}^{nnS}<{\tilde{c}}^{dnI}<{\tilde{c}}^{dnS}<{\tilde{c}}^{ddI}<{\tilde{c}}^{ddS}$.

dd We only need to compare $\pi ^{ddk}_2$ and $\pi ^{dnl}_2$, where $k,l=S$ or I. Based on two types of market statuses in the nn and dn subgames, we need to consider the following four cases:

• (1) If dd then S, and if dn then S ( $c\ge \max \{{\tilde{c}}^{ddS},{\tilde{c}}^{dnS}\}={\tilde{c}}^{ddS}$). If this is the case, $\pi ^{ddS}_2\ge \pi ^{dnS}_2$ always holds. Therefore, dd is the equilibrium outcome.

• (2) If dd then S, if dn then I (${\tilde{c}}^{ddS}\le c\le {\tilde{c}}^{dnI}$). However, from Remark 2, we know that ${\tilde{c}}^{dnI}<{\tilde{c}}^{ddS}$ always holds. Therefore, dd cannot be the equilibrium outcome.

• (3) If dd then I, and if dn then S (${\tilde{c}}^{dnS}\le c\le {\tilde{c}}^{ddI}$). If this is the case, $\pi ^{dnS}_2>\pi ^{ddI}_2$ always holds. Therefore, dd cannot be the equilibrium outcome.

• (4) If dd then I, and if dn then I ($c\le \min \{{\tilde{c}}^{ddI},{\tilde{c}}^{dnI}\}={\tilde{c}}^{dnI}$). If this is the case, $\pi ^{ddI}_2>\pi ^{dnI}_2$ always holds. Therefore, dd is the equilibrium outcome.

To summarize, dd is the equilibrium outcome when the inequality in part (i) of Proposition 1 holds.

dn or nd For symmetry, it suffices to consider only the case of dn. We need to compare $\pi ^{dnk}_1$ and $\pi ^{nnl}_1$, and $\pi ^{dnk}_2$ and $\pi ^{ddl}_2$ where $k,l=S$ or I. Based on two types of market statuses in the dn, nn and dd subgames, we need to consider the following eight cases:

• (1) If dn then S, if nn then S, and if dd then S ($c\ge \max \{{\tilde{c}}^{dnS},{\tilde{c}}^{nnS},{\tilde{c}}^{ddS}\} ={\tilde{c}}^{ddS}$). If this is the case, $\pi ^{ddS}_2>\pi ^{dnS}_2$ always holds. Therefore, dn cannot be the equilibrium outcome.

• (2) If dn then S, if nn then S, and if dd then I ($\max \{{\tilde{c}}^{dnS},{\tilde{c}}^{nnS}\}={\tilde{c}}^{dnS}\le c\le {\tilde{c}}^{ddI}$). If this is the case, $\pi ^{dnS}_1\ge \pi ^{nnS}_1$, and $\pi ^{dnS}_2\ge \pi ^{ddI}_2$. Therefore, dn is the equilibrium outcome.

• (3) If dn then S, and if nn then I, if dd then S ($\max \{{\tilde{c}}^{dnS},{\tilde{c}}^{ddS}\}={\tilde{c}}^{ddS}\le c\le {\tilde{c}}^{nnI}$). However, from Remark 2, we know that ${\tilde{c}}^{nnI}<{\tilde{c}}^{ddS}$ always holds. Therefore, dn cannot be the equilibrium outcome.

• (4) If dn then S, and if nn then I, if dd then I (${\tilde{c}}^{dnS}\le c\le \min \{{\tilde{c}}^{nnI},{\tilde{c}}^{ddI}\}={\tilde{c}}^{nnI}$). However, from Remark 2, we know that ${\tilde{c}}^{nnI}<{\tilde{c}}^{dnS}$ always holds. Therefore, dn cannot be the equilibrium outcome.

• (5) If dn then I, if nn then I, and if dd then I ($c\le \min \{{\tilde{c}}^{dnI},{\tilde{c}}^{nnI},{\tilde{c}}^{ddI}\} ={\tilde{c}}^{nnI}$). If this is the case, $\pi ^{ddI}_2>\pi ^{dnI}_2$ always holds. Therefore, dn cannot be the equilibrium outcome.

• (6) If dn then I, if nn then I, and if dd then S (${\tilde{c}}^{ddS}\le c\le \min \{{\tilde{c}}^{dnI},{\tilde{c}}^{nnI}\}={\tilde{c}}^{nnI}$). However, from Remark 2, we know that ${\tilde{c}}^{nnI}<{\tilde{c}}^{ddS}$ always holds. Therefore, dn cannot be the equilibrium outcome.

• (7) If dn then I, if nn then S, and if dd then I (${\tilde{c}}^{nnS}\le c\le \min \{{\tilde{c}}^{dnI},{\tilde{c}}^{ddI}\}={\tilde{c}}^{dnI}$). If this is the case, $\pi ^{ddI}_2>\pi ^{dnI}_2$ always holds. Therefore, dn cannot be the equilibrium outcome.

• (8) If dn then I, if nn then S, and if dd then S ($\max \{{\tilde{c}}^{nnS},{\tilde{c}}^{ddS}\}={\tilde{c}}^{ddS}\le c\le {\tilde{c}}^{dnI}$). However, from Remark 2, we know that ${\tilde{c}}^{dnI}<{\tilde{c}}^{ddS}$ always holds. Therefore, dn cannot be the equilibrium outcome.

To summarize, dn and nd are the equilibrium outcomes when the inequality in Proposition 1 (ii) holds.

nn We compare $\pi ^{nnk}_1$ and $\pi ^{dnl}_1$, where $k,l=S$ or I. Based on two types of market statuses in the nn and dn subgames, we need to consider the following four cases:

• (1) If nn then S, and if dn then S ($c\ge \max \{{\tilde{c}}^{nnS},{\tilde{c}}^{dnS}\}={\tilde{c}}^{dnS}$). If this is the case, $\pi ^{dnS}_1>\pi ^{nnS}_1$ always holds. Therefore, nn cannot be the equilibrium outcome.

• (2) If nn then S, and if dn then I (${\tilde{c}}^{nnS}\le c\le {\tilde{c}}^{dnI}$). If this is the case, $\pi ^{nnS}_1\ge \pi ^{dnI}_1$ always holds. Therefore, nn is the outcome.

• (3) If nn then I, and if dn then S (${\tilde{c}}^{dnS}\le c\le {\tilde{c}}^{nnI}$). However, from Remark 2, we know that ${\tilde{c}}^{nnI}<{\tilde{c}}^{dnS}$ always holds. Therefore, nn cannot be the equilibrium outcome.

• (4) If nn then I, and if dn then I ($c\le \min \{{\tilde{c}}^{nnI},{\tilde{c}}^{dnI}\}={\tilde{c}}^{nnI}$). If this is the case, $\pi ^{dnI}_1>\pi ^{nnI}_1$ always holds. Therefore, nn cannot be the equilibrium outcome.

To summarize, nn is the equilibrium outcome when the inequality in Proposition 1 (iii) holds.

1.4 Proof of Lemma 5, Proposition 2 and 3

We first prove Lemma 5. When both firms choose not to delegate, the incentive rates are $\hat{{\varvec{\theta }}}^{nn}\equiv (1,1)$. When one firm chooses to delegate, the incentive rates are given in Eqs. (18) and (19). When both firms choose to delegate, we substitute $c_1=c+\varDelta$ an $c_2=c$ to Eq. (7) and obtain ${\hat{{\varvec{q}}}}^{dd}(\theta _1,\theta _2)$. In Stage 2, firms’ incentive rates are derived as follow:

$$\begin{aligned} \begin{array}{ll} Status\ S:\ &{} {\left\{ \begin{array}{ll} &{}\max _{\theta _1}(P^S(\hat{{\varvec{q}}}^{ddS}(\theta _1,\theta _2))-c) {\hat{q}}^{ddS}_1(\theta _1,\theta _2)\\ &{}\max _{\theta _2}(P^S(\hat{{\varvec{q}}}^{ddS}(\theta _1,\theta _2))-c) {\hat{q}}^{ddS}_2(\theta _1,\theta _2) \end{array}\right. } \Rightarrow \hat{{\varvec{\theta }}}^{ddS}=\left( \begin{array}{ll} &{}\displaystyle \frac{6}{5}-\frac{1-2\varDelta }{5(c+\varDelta )},\\ &{}\displaystyle \frac{6}{5}-\frac{1+2\varDelta }{5c} \end{array}\right) , \\ Status\ I:\ &{} {\left\{ \begin{array}{ll} &{}\max _{\theta _1}(P^I(\hat{{\varvec{q}}}^{ddI}(\theta _1,\theta _2))-c) {\hat{q}}^{ddI}_1(\theta _1,\theta _2)\\ &{}\max _{\theta _2}(P^I(\hat{{\varvec{q}}}^{ddI}(\theta _1,\theta _2))-c) {\hat{q}}^{ddI}_2(\theta _1,\theta _2) \end{array}\right. } \Rightarrow \hat{{\varvec{\theta }}}^{ddI}=\left( \begin{array}{ll} &{}\displaystyle \frac{6}{5}-\frac{2a-2(1+a)\varDelta }{5(1+a)(c+\varDelta )},\\ &{}\displaystyle \frac{6}{5}-\frac{2a+2(1+a)\varDelta }{5(1+a)c} \end{array}\right) . \end{array} \end{aligned}$$

We substitute ${\hat{{\varvec{\theta}}}}^{nnS}$, ${\hat{{\varvec{\theta}}}}^{nnI}$, ${\hat{{\varvec{\theta}}}}^{dnS}$, ${\hat{{\varvec{\theta}}}}^{dnI}$, ${\hat{{\varvec{\theta}}}}^{ndS}$, ${\hat{{\varvec{\theta}}}}^{ndI}$, ${\hat{{\varvec{\theta}}}}^{ddS}$, ${\hat{{\varvec{\theta}}}}^{ddI}$ to Eq. (6), we can derive the threshold values of ${\bar{q}}_j$ that define each firm’s discontinuous reaction function. Substituting these incentive rates to Eq. (7), we can obtain firms’ equilibrium quantities. By further substituting the equilibrium quantities to Eq. (2), we can obtain firms’ equilibrium profits. The equilibrium values are summarized in Table 2.

Table 2 Equilibrium outcomes with $Z\equiv (a+1)/a$

We first need the market to separate under dn and nd, from which we have

$$\begin{aligned} \begin{array}{ll} dn: &{\left\{ \begin{array}{ll} {\hat{q}}_1^{dnS}\le {\bar{q}}_1(\hat{{\varvec{\theta }}}^{dnS}),\\ {\hat{q}}_2^{dnS}\le {\bar{q}}_2(\hat{{\varvec{\theta }}}^{dnS}) \end{array}\right. } \Rightarrow c\ge {\hat{c}}^{dnS}\equiv \displaystyle \frac{5 + 28 a + 16 a^2-16(a-a^2)\sqrt{Z}}{25 + 24 a}-\frac{2(15+16a-8a\sqrt{Z})}{25-24a}\varDelta ,\\ nd: & {\left\{ \begin{array}{ll} {\hat{q}}_1^{ndS}\le {\bar{q}}_1(\hat{{\varvec{\theta }}}^{ndS}),\\ {\hat{q}}_2^{ndS}\le {\bar{q}}_2(\hat{{\varvec{\theta }}}^{ndS}) \end{array}\right. } \Rightarrow c\ge {\hat{c}}^{ndS}\equiv \displaystyle \frac{5 + 28 a + 16 a^2-16(a-a^2)\sqrt{Z}}{25 + 24 a}-\frac{5+8a-16a\sqrt{Z}}{25-24a}\varDelta . \\ \end{array} \end{aligned}$$

We also need the market to integrate under dd, from which we have

$$\begin{aligned} {\left\{ \begin{array}{ll} {\hat{q}}_1^{ddI}\ge {\bar{q}}_1(\hat{{\varvec{\theta }}}^{ddI}),\\ {\hat{q}}_2^{ddI}\ge {\bar{q}}_2(\hat{{\varvec{\theta }}}^{ddI}) \end{array}\right. } \Rightarrow c\le {\hat{c}}^{ddI}\equiv \displaystyle \frac{a + 17 a^2 + 10 a^3-10a(1-a^2)\sqrt{1/Z}}{2 (1 + a) ( 8 a-1)}+\displaystyle \frac{3+6a+10(1+a)\sqrt{1/Z}}{ 8 a-1}\varDelta . \end{aligned}$$

It is straightforward that ${\hat{c}}^{dnS}<{\hat{c}}^{ndS}$. Moreover, ${\hat{c}}^{ndS}<{\hat{c}}^{ddI}$ if and only if $a>0.734$ and

$$\begin{aligned} \varDelta \le \displaystyle \frac{(1-a)(8 a^3+ 15 a^2-16a- 14 )}{4(1+a)(8a^2+47a+64)}-\frac{(2 - 17 a + 7 a^2 + 8 a^3)\sqrt{1/Z}}{4(64 + 47 a + 8 a^2)}. \end{aligned}$$

It can also be confirmed that for ${\hat{c}}^{dnS}\le c\le {\hat{c}}^{ddI}$, the market always separates under nn.

Because all equilibrium profits in Table 2 are continuous in $\varDelta$, all our arguments in the case of firms’ identical marginal costs hold for $\varDelta \rightarrow 0$. Therefore, for sufficiently small $\varDelta$ and when ${\hat{c}}^{dnS}\le c\le {\hat{c}}^{ddI}$, ${\hat{\pi }}_1^{dnS}>{\hat{\pi }}_1^{nnS}$ and ${\hat{\pi }}_2^{dnS}>{\hat{\pi }}_2^{ddI}$. Moreover, for sufficiently small $\varDelta$ and when ${\hat{c}}^{ndS}\le c\le {\hat{c}}^{ddI}$, ${\hat{\pi }}_1^{ndS}>{\hat{\pi }}_1^{ddI}$ and ${\hat{\pi }}_2^{ndS}>{\hat{\pi }}_2^{nnS}$. Therefore, we can confirmed that the dn equilibrium presents when ${\hat{c}}^{dnS}\le c\le {\hat{c}}^{ddI}$, and that the nd equilibrium presents when ${\hat{c}}^{ndS}\le c\le {\hat{c}}^{ddI}$.

Proposition 2 follows straightforwardly from Lemma 5. Regarding Proposition 3, by comparing ${\hat{\pi }}^{dnS}_1$ and ${\hat{\pi }}^{dnS}_2$, we can confirm that Firm 1’s profit is larger when $\varDelta$ is sufficiently small.