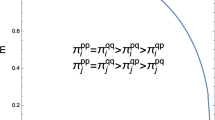Endogenous strategic variable in a mixed duopoly

Abstract

In this paper we endogenize the choice of strategic variables in a mixed duopoly market in which each firm produces a homogeneous product with a strictly increasing convex cost function. This allows us to endogenously determine the type of competition in a mixed duopoly. We get the interesting result that price competition is a dominant strategy for each firm in a mixed duopoly. The firms randomize among the prices belonging to the equilibrium range of price in Bertrand competition. It is different from the outcome in a simple duopoly market where both price competition and quantity competition are pure strategy Nash equilibrium. Thus, this paper establishes that the presence of a public firm influences the kind of competition that takes place in a duopoly market.

Appendix

1.1 Proof of Lemma 1

Suppose $q_{2}=0$. From Eq. (1) we get, $f(p_{1})+p_{1}f^{\prime }(p_{1})-c^{\prime }(f(p_{1}))f^{\prime }(p_{1})=0$.

$p_{1}$ satisfying the Eq. (1) at $q_{2}=0$ is $p^{M}$, monopoly price. For $q_{2}=0$, we get that $p^{Max}$ satisfies the Eq. (2) i.e. $f(p^{Max})=0$. We know that $p^{M}<p^{Max}$. Thus, we get the intercept of the reaction function of firm 1, $\gamma _{1}(q_{2})=p_{1}$ is less than the intercept of the reaction function of firm 2, $\gamma _{2}(p_{1})=q_{2}$ at $q_{2}=0$. Suppose $p_{1}=0$, Eq. (2) gives us $f(0)=2q_{2}$. So $Q^{Max}=2q_{2}~$ at $~p_{1}=0$. Putting $p_{1}=0$ and $q_{2}=\frac{Q^{Max}}{2}~$ in the Eq. (1), we get, $f(0)-\frac{Q^{Max}}{2}-c^{\prime }(f(0)-\frac{Q^{Max}}{2})f^{\prime }(0)$.

This implies $\frac{Q^{Max}}{2}-c^{\prime }(\frac{Q^{Max}}{2})f^{\prime }(0)>0~$, since $~f^{\prime }(0)<0$. For the Eq. (1) to hold at $q_{2}=\frac{Q^{Max}}{2},~$ we need $p_{1}>0$ as $\gamma _{1}^{\prime }(q_{2})<0$. This implies that the reaction function $~\gamma _{1}(\frac{Q^{Max}}{2})=p_{1}~$ is such that $p_{1}>0$. But the reaction function of firm 2 at $q_{2}=\frac{Q^{Max}}{2}~$ is such that $~\gamma _{2}(0)=\frac{Q^{Max}}{2}$. Therefore, at $(p_{1}=0, q_{2}=\frac{Q^{Max}}{2})$ the reaction function of firm 1 lies above the reaction function of firm 2. The reaction function of firm 1 lies below the reaction function of firm 2 at $q_{2}=0$ and the reaction function of firm 1 lies above the reaction of firm 2 at $q_{2}=\frac{Q^{Max}}{2}$. We already know that $~\gamma _{1}^{\prime }(q_{2})<0,~ \forall q_{2}\ge 0$ and $\gamma _{2}^{\prime }(p_{1})<0, ~ \forall p_{1}\ge 0$. Therefore, the reaction functions $~\gamma _{1}(q_{2})=p_{1}$ and $~\gamma _{2}(p_{1})=q_{2}$ must intersect at a unique point $(p_{1}, q_{2})$ such that $(p_{1}^{A*}, q_{2}^{A*})>0$. $(p_{1}^{A*}, q_{2}^{A*})>0$ maximizes $\pi _{1}(p^{A}_{1},q_{2}^{A})~\text{ and }~sw_{1}(p^{A}_{1},q_{2}^{A})$, as being a point on the reaction function of each firm. $\square$

1.2 Proof of Lemma 2

Suppose $q_{1}=0$, from Eq. (5), we get, $p_{2}=c^{\prime }(0)$. From Eq. (6), we get, $p_{2}=c^{\prime }(f(p_{2}) )$. Thus, we find that the intercept of the reaction function of firm 2 $\mu _{2}(0)=p_{2}$ lies above the intercept of the reaction function of firm 1. We have already shown that $\mu ^{\prime }_{1}(p_{2})>0$ and $\mu ^{\prime }_{2}(q_{1})<0$. Thus, the reaction function of firm 1 $\mu _{1}(p_{2})=q_{2}$ is going to intersect the reaction function of firm 2 $\mu _{2}(q_{1})=p_{2}$ at a unique point $(q_{1}^{D*},p_{2}^{D*})>0$. This point lies in both the reaction functions so it maximizes $\pi _{1}^{D}$ and $sw_{2}^{D}$. $\square$

1.3 Proof of Lemma 3

From Eqs. (1) and (2), we get: $f(p^{A})-q_{2}+p^{A}f^{\prime }(p^{A})-c^{\prime }(f(p^{A})-q_{2})f^{\prime }(p^{A})=0$, and $q_{1}^{A}=q_{2}^{A}$, at equilibrium. From Eqs. (3) and (4), we get, $g(q_{1}+q_{2})+g^{\prime }(q_{1}+q_{2})q_{1}-c^{\prime }(q_{1})=0$, and $g(q_{1}+q_{2})-c^{\prime }(q_{2})=0$. In equilibrium, the Eq. (3) is $c^{\prime }(q_{2})+g^{\prime }(q_{1}+q_{2})q_{1}-c^{\prime }(q_{1})=0.$ We insert the equilibrium condition of case A, $~q_{1}^{A}=q_{2}^{A}~$ in the above equilibrium condition of case C and get, $g^{\prime }(q_{1}+q_{2})q_{1}=0$, but $~g^{\prime }(q_{1}+q_{2})q_{1}<0$, for $q_{1}^{A}>0, q_{2}^{A}>0$. Therefore, the first order condition of firm 1 in case C is negative when we put $q_{1}=q_{1}^{A}$ and $q_{2}=q_{2}^{A}$. This implies that at equilibrium, $q_{1}^{A}>q_{1}^{C}$. Through a similar argument, we can show that $q_{2}^{A}<q_{2}^{C}$.

In case C, we get $p=c^{\prime }(q_{2}^{C})$ from Eq. (4). Inserting the above condition in Eq. (1), we get $f(p^{C})-q_{2}^{A}+f^{\prime }(p)[c^{\prime }(q_{2}^{C})-c^{\prime }(f(p)-q_{2})]=0$. This implies $f(p^{C})-q_{2}^{A}=0$, since $c^{\prime }(q_{2}^{C})=c^{\prime }(f(p)-q_{2})$ at equilibrium in case A. But $q_{1}^{A}>0$. Therefore, Eq. (1) is $f(p^{C})-q_{2}^{A}>0$, so $~p=p^{C}~$ is not optimal. $~p^{A}>p^{C}$ since Eq. (1) is positive at $p^{C}$. $\square$

1.4 Proof of Lemma 4

Suppose $[c^{\prime }(q_{1}^{A})-\dfrac{c(q_{1}^{A})}{q_{1}^{A}}]q_{1}^{A}-[c^{\prime }(q_{1}^{C})-\dfrac{c(q_{1}^{C})}{q_{1}^{C}}]q_{1}^{C}>0$.

$$\begin{aligned} \pi _{1}^{A}-\pi _{1}^{C}= p^{A}_{1}q_{1}^{A}-c(q_{1}^{A})-g(q_{1}^{C}+q_{2}^{C})q_{1}^{C}+c(q_{1}^{C}). \end{aligned}$$

(7)

From Eq. (1), we get $p^{A}_{1}=c^{\prime }(q_{1}^{A})-\frac{q_{1}^{A}}{f^{\prime }(p^{A}_{1})}$. From Eq. (3), we get $g(q_{1}^{C}+q_{2}^{C})+g^{\prime }(q_{1}^{C}+q_{2}^{C})q_{1}^{C}-c^{\prime }(q_{1}^{C})=0$. Substituting for $p^{A}$ and $g(q_{1}^{C}+q_{2}^{C})$ in Eq. (7), we get,

$[c^{\prime }(q_{1}^{A})-\frac{q_{1}^{A}}{f^{\prime }(p^{A}_{1})}]q_{1}^{A}-c(q_{1}^{A})-[c^{\prime }(q_{1}^{C})-g^{\prime }(q_{1}^{C}+q_{2}^{C})q_{1}^{C}]q_{1}^{C}+c(q_{1}^{C})$. We know $g^{\prime }()=\frac{1}{f^{\prime }()}$, since $g(Q)=p$ and $f(p)=Q$. This implies $[c^{\prime }(q_{1}^{A})-\frac{q_{1}^{A}}{f^{\prime }(p^{A}_{1})}]q_{1}^{A}-c(q_{1}^{A})-[c^{\prime }(q_{1}^{C})-\frac{q_{1}^{C}}{f^{\prime }(p^{C})}]q_{1}^{C}+c(q_{1}^{C})$. We know $q_{1}^{A}>q_{1}^{C}$ and $p^{A}>p^{C}, \text{ implying }~ f^{\prime }(p^{A})<f^{\prime }(p^{C})$, since f() is a downward sloping concave function.

This implies $-\dfrac{(q_{2}^{A})^{2}}{f^{\prime }(p^{A})}+\dfrac{(q_{1}^{C})^{2}}{f^{\prime }(p^{C})}>0$ that gives us $\pi _{1}^{A}-\pi _{1}^{C}>0$, since $[c^{\prime }(q_{1}^{A})-\dfrac{c(q_{1}^{A})}{q_{1}^{A}}]q_{1}^{A}-[c^{\prime }(q_{1}^{C})-\dfrac{c(q_{1}^{C})}{q_{1}^{C}}]q_{1}^{C}>0$. $\square$

1.5 Proof of Lemma 5

From Eq. 4, we have $g(q_{1}^{C}+q_{2}^{C})-c^{\prime }(q_{2}^{C})=0$. This implies $c^{\prime -1}(p)=q_{2}^{C}$.

From Eq. (3), we have $g(q_{1}^{C}+q_{2}^{C})+g^{\prime }(q_{1}^{C}+q_{2}^{C})q_{1}^{C}=c^{\prime }(q_{1}^{C})$ resulting $q_{1}^{C}=c^{\prime -1}(p+ g^{\prime }(q_{1}^{C}+q_{2}^{C})q_{1}^{C})$. So $Q^{C}=q_{1}^{C}+q_{2}^{C}=c^{\prime -1}(p+ g^{\prime }(q_{1}^{C}+q_{2}^{C})q_{1}^{C})+ c^{\prime -1}(p)$.

$$\begin{aligned} f^{C}(p)=c^{\prime -1}(p+ g^{\prime }(q_{1}^{C}+q_{2}^{C})q_{1}^{C})+ c^{\prime -1}(p) \end{aligned}$$

(8)

From Eq. (5), $p=c^{\prime }(q_{1}^{D})$. This implies $c^{\prime -1}(p)=q_{1}^{D}$. From Eq. (6),

$f^{\prime }(p)p-c^{\prime }(f(p)-q_{1}^{D})f^{\prime }(p)=0$ leads to $p-c^{\prime }(q_{2}^{D})=0$. So $q_{2}^{D}=c^{\prime -1}(p)$.

$$\begin{aligned} Q^{D}=q_{1}^{D}+q_{2}^{D}=f^{D}(p)=2c^{\prime -1}(p) \end{aligned}$$

(9)

Comparing Eqs. (8) and (9), we get, $c^{\prime -1}(p+g^{\prime }()q_{1}^{C})+c^{\prime -1}(p)<~2c^{\prime -1}(p)$.

$g^{\prime }()q_{1}^{C}<0~$, because g() is a downward sloping concave function and c() is strictly convex increasing function. $f^{C}(p)<f^{D}(p)$. $p^{D}<p^{C}$, since f(p) is a downward sloping concave function. $\square$

1.6 Proof of Lemma 6

Suppose $sw_{2}^{D}-sw_{2}^{C}>0$. This implies

$\left[ \displaystyle {\int }_{p^{D}}^{p^{Max}}f(x)dx+p^{D}q_{1}^{D}-c(q_{1}^{D})+p^{D}\left[ f(p^{D})-q_{1}^{D}\right] -c(f(p^{D})-q_{1}^{D})\right] -\left[ \displaystyle {\int }_{0}^{Q_{C}}g(x)dx-c(q_{1}^{C})-c(q_{2}^{C})\right] >0$. So $\displaystyle {\int }_{p^{D}}^{p^{Max}}f(x)dx -c(q_{1}^{D})+p^{D}f(p^{D})-c(f(p^{D})-q_{1}^{D})+\int _{p^{C}}^{p^{Max}}f(x)dx-p^{C}\left[ q_{1}^{C}+q_{2}^{C}\right] +c(q_{1}^{C})+c(q_{2}^{C})>0$. From Lemma 5, we know that $p^{C}>p^{D}$ and from Lemma 2$q_{1}^{D}=q_{2}^{D}$, so we get, $\displaystyle {\int }_{p^{D}}^{p^{C}}f(x)dx + p^{D}f(p^{D})-p^{C}[q_{1}^{C}+q_{2}^{C}]-2c(q_{1}^{D})+c(q_{1}^{C})+c(q_{2}^{C})>0$.

This implies $\displaystyle {\int }_{Q^{C}}^{Q^{D}}g(x)dx-2c(q_{1}^{D})+c(q_{1}^{C})+c(q_{2}^{C})>0$.

The sufficiency aspect is obvious. $\square$

1.7 Proof of Lemma 8

We know that $\bar{p}$ is such that $\dfrac{c(f(p)-c(\frac{f(p)}{2})}{\frac{f(p)}{2}}\ge p$. From Lemma 2, we get $p^{D}_{2}=c^{\prime }(\frac{f(p^{D}_{2})}{2})$. From the convexity of the cost function we get,

$\dfrac{c(f(p_{2}^{D})-c(\frac{f(p_{2}^{D})}{2}))}{\frac{f(p_{2}^{D})}{2}}>c^{\prime }(\frac{f(p_{2}^{D})}{2})$. Thus, $p^{D}_{2}<\bar{p}$. The other part is obvious since at $\underline{p}$, $\hat{\pi _{1}}(\underline{p})_=-c(0)$. But $\pi _{1}^{D}>0$, so $\underline{p}<p_{2}^{D}$. $\square$

1.8 Proof of Lemma 9

Suppose $p^{A}\le \bar{p}$ and suppose $\dfrac{c(f(p^{A}))-c(\frac{f(p^{A})}{2}))}{\frac{f(p^{A})}{2}}<c^{\prime }(\frac{f(p^{A})}{2})-\dfrac{(q_{1}^{A})^{2}}{f^{\prime }(p^{A})}$.

This implies $\dfrac{c(f(p^{A}))-c(\frac{f(p^{A})}{2}))}{\frac{f(p^{A})}{2}}<p^{A}$, because from Eq. (1), at equilibrium, we get $p^{A}=c^{\prime }(\frac{f(p^{A})}{2})-\dfrac{(q_{1}^{A})^{2}}{f^{\prime }(p^{A})}$. This implies $c(f(p^{A}))-c(\frac{f(p^{A})}{2})<p^{A}\dfrac{f(p^{A})}{2}.$$p^{A}\dfrac{f(p^{A})}{2}-c(\frac{f(p^{A})}{2})<p^{A}f(p^{A})-c(f(p^{A}))$. So $p^{A}>\bar{p}$, from the results on price competition in a mixed duopoly. This results in a contradiction. Therefore,

$$\begin{aligned} \dfrac{c(f(p^{A}))-c(\frac{f(p^{A})}{2}))}{\frac{f(p^{A})}{2}}>c^{\prime }(\frac{f(p^{A})}{2})-\dfrac{(q_{1}^{A})^{2}}{f^{\prime }(p^{A})}. \end{aligned}$$

The sufficiency aspect is obvious from the convexity of the cost function. $\square$

1.9 Proof of Lemma 10

$P_{2}$ lies in [0, 1] because $\hat{\pi }_{1}(p^{A})-\pi _{1}(p^{D})>0$ and $\hat{\pi }_{1}(p^{D})>0$. $\hat{\pi }_{1}(p^{A})-\pi _{1}(p^{D})>0$ is true because $p^{A} > p^{D}$ and $p^{A} , p^{D} \in [\underline{p},\bar{p}]$ where $~\hat{\pi }_{1}(p)>\pi _{1}(p)~\forall p\in [\underline{p},\bar{p}]$ and $\hat{\pi }_{1}'(p)>0,\forall p<p^{m}$. $\hat{\pi }_{1}(p^{D})>0$ because $p^{D}=c'(\frac{f(p^{D})}{2})$ and from the strict convexity of cost function, we have $c'(\frac{f(p)}{2})>\dfrac{c(\frac{f(p)}{2})}{\frac{f(p)}{2}}$.

We need to show that $0<P_{1}<1$. Using convexity of cost function it is easy to show that $\hat{sw}(p)>sw(p)$, $\forall p>0$. This implies $\hat{sw}(p^{D})-sw(p^{D})+\hat{sw}(p^{A})-sw(p^{A})>0$. For $\hat{sw}(p^{A})-sw(p^{D})>0$ we need the condition $c(Q^{A})- \displaystyle {\int }_{Q^{A}}^{Q^{D}}g(x)dx -2c(\frac{Q^{A}}{2})>0$. Suppose $\hat{sw}(p^{A})-sw(p^{D})>0$. It implies $\displaystyle {\int }_{p^{A}}^{p^{Max}}f(x)dx+p^{A}f(p^{A})-2c(\frac{f(p^{A})}{2})-\int _{p^{D}}^{p^{Max}}f(x)dx -p^{D}f(p^{D})+c(f(p^{D}))>0.$ Thus, $c(Q^{D})-\int _{Q^{A}}^{Q^{D}}g(x)dx-2c(\frac{Q_{A}}{2})>0$. This is both a necessary and a sufficient condition. We assume that $c(Q^{A})- \displaystyle {\int }_{Q^{A}}^{Q^{D}}g(x)dx -2c(\frac{Q^{A}}{2})>0$ is true. So $P_{1}$ lies in (0, 1). $\square$

1.10 Proof of Proposition 11

Suppose firm 1 chooses price and randomizes between $p^{A}$ and $p^{D}$ with the probability of setting $p^{D}$ as $P_{1}=\dfrac{\hat{sw}(p^{A})-sw(p^{D})}{\hat{sw}(p^{D})-sw(p^{D})+\hat{sw}(p^{A})-sw(p^{A})}$. It is not optimal for firm 2 to choose quantity in stage one. If firm 2 chooses quantity then the pay-off of firm 2 is $sw(p^{A})\times P_{1}+(1-P_{1})\times \hat{sw}(p^{A})$ and $sw(p^{A})\times P_{1}+(1-P_{1})\times \hat{sw}(p^{A})<Exp(\hat{sw}(P_{1},P_{2}))$. So firm 2 should switch to price in stage one. Therefore, the possibility of case A is ruled out.

Suppose firm 2 chooses price and randomizes between $p^{A}$ and $p^{D}$ with the probability of setting $p^{D}$ as $P_{2}=\dfrac{\hat{\pi }_{1}(p^{A})-\pi _{1}(p^{D})}{\hat{\pi }_{1}(p^{D})+\hat{\pi }_{1}(p^{A})-\pi _{1}(p^{D})}$. If firm 1 chooses quantity then its pay-off is $P_{2}\times \hat{\pi }(p^{D})+(1-P_{2})\times \pi _{1}(p^{D})$ and it is less than $Exp(\hat{\pi }_{1}(P_{1},P_{2})$. So firm 1 should switch to price in stage one. Therefore, the possibility of case D is ruled out.

Suppose firm 1 randomizes between price $p^{A}$ and $p^{D}$, and firm 2 randomizes between $p^{D}$ and $p^{*}$, $p^{*}<p^{A}$. The expected pay-off of firm 2 from $p^{*}$ is $sw(p^{*})\times P_{1}+(1-P_{1})\times sw(p^{*})$ when firm 1 randomizes between $p^{D}$ and $p^{A}$. $sw(p^{*})\times P_{1}+(1-P_{1})\times sw(p^{*}) < \hat{sw}(p^{A})\times P_{1}+(1-P_{1})\times sw(p^{A})$, since $\hat{sw}(p)>sw(p), \forall p \in [\underline{p},\bar{p}]$. sw(p) is maximized at $p^{S}=c'(f(p^{S}))$ and $p^{S}>p^{A}$ from the convexity of the cost function. Thus, there is no tendency for firm 2 to undercut the price at $p^{A}$. Firm 2 has no tendency to undercut the price at $p^{D}$ because $\hat{sw}(p)=\displaystyle {\int }_{p}^{p^{Max}}f(x)dx +pf(p)-2c(\frac{f(p)}{2})$ is maximized at $p=p^{D}$. Thus, when firm 1 randomizes between $p^{A}$ and $p^{D}$, the optimal strategy of firm 2 is to randomize between the same prices with the probability of setting $p^{D}$ price as $P_{2}= \dfrac{\hat{\pi }_{1}(p^{A})-\pi _{1}(p^{D})}{\hat{\pi }_{1}(p^{D})+\hat{\pi }_{1}(p^{A})-\pi _{1}(p^{D})}$.

$\hat{\pi }_{1}(p)>\pi _{1}(p), \forall ~p\in [\underline{p},\bar{p})$ and $\hat{\pi }_{1}(p)=\pi _{1}(p)$ at $p=\bar{p}$. So there is no tendency for firm 1 to undercut at $p^{D}$ and $p^{A}$ when firm 2 randomizes between $p^{A}$ and $p^{D}$.

Thus, $\{P_{1},P_{2}\}$ such that $P_{1}=\dfrac{\hat{sw}(p^{A})-sw(p^{D})}{\hat{sw}(p^{D})-sw(p^{D})+\hat{sw}(p^{A})-sw(p^{A})}$,

$P_{2}=\dfrac{\hat{\pi }_{1}(p^{A})-\pi _{1}(p^{D})}{\hat{\pi }_{1}(p^{D})+\hat{\pi }_{1}(p^{A})-\pi _{1}(p^{D})}~$ is a non-degenerate asymmetric mixed strategy Nash equilibrium where firm 1 and firm 2 randomize between the prices $p^{A}$ and $p^{B}$. $\square$