Abstract
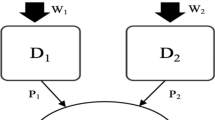
We consider a vertical relationship where an upstream monopolist supplies input to downstream duopolistic firms. Under the assumption that downstream firms produce under a soft capacity restriction, we show that the balance between price and quantity in downstream firms’ strategy is endogenous. In this way, the monopolist’s charge for input co-determines downstream market conduct. We spell out some consequences of this, for example, that an increase of downstream capacity costs can result in increased output. We discuss other implications in relation to pass-through and incidence of cost changes.


Similar content being viewed by others
Notes
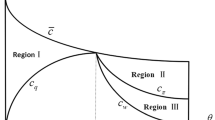
As described by Kreps and Scheinkman (1983), price competition under capacity pre-commitment sustains Cournot equilibrium when capacity constraints imply that marginal costs are prohibitively high once production volume equals capacity. Hard capacity restrictions might be thought to be fitting for “transfer line” technologies like the one introduced by Henry Ford.
The model is a simplified version of that of Maggi (1996). For this reason the description and parts of the analysis are kept short.
\(p_i^b \left( \theta \right) =\left( {2-d} \right) ^{-1}\left( {\left( {1-d} \right) a+\theta +\omega } \right) \) and \(q_i^b \left( \theta \right) =\left( {\left( {2-d} \right) \left( {1+d} \right) } \right) ^{-1}\left( {a-\left( {\theta +\omega } \right) } \right) \) and total sale is \(Q^{b}\left( \omega \right) =2\left( {\left( {1+d} \right) \left( {2-d} \right) } \right) ^{-1}\left( {a-\theta -\omega } \right) \).
\(p_i^c \left( \psi \right) =\left( {2+d} \right) ^{-1}\left( {a+\left( {1+d} \right) \left( {\psi +\omega } \right) } \right) \) and \(q_i^c \left( \psi \right) =\left( {2+d} \right) ^{-1}\left( {a-\left( {\psi +\omega } \right) } \right) ,\) and total sale is \(Q^{c}\left( \omega \right) =2\left( {2+d} \right) ^{-1}\left( {a-\psi -\omega } \right) \).
This solves for \(\hat{\theta } \left( {\omega , \psi } \right) =\left( {2+d} \right) ^{-1}\left( {d^{2}\left( {a-\omega } \right) +\left( {1+d} \right) \left( {2-d} \right) \psi } \right) \).
We would like to thank a referee for drawing attention to this issue. However, when the upstream monopolist uses a two-part tariff with a payment given by \(P= A+\omega q_{i}\) there is flexibility with respect to how much downstream firms produce and a variant of Proposition 1 survives. It is beyond the scope of this paper to analyze this, but it is clearly of interest to ask how the result in Proposition 1 can be modified under different assumptions about forcing contracts.
References
Horn H, Wolinsky A (1988) Bilateral monopolies and incentives for merger. RAND J Econ 19(3):408–419
Inderst R, Shaffer G (2010) Market-share contracts as facilitating practices. RAND J Econ 41(1):709–729
Innes R, Hamilton S (2009) Vertical restraints and horizontal control. RAND J Econ 40(1):120–143
Karp LS, Perloff JM (2013) Vertical contracts and mandatory universal distribution. BE J Econ Anal Policy 13(2):595–626
Kitamura H, Miyaoka A, Sato M (2016) Relation-specific investment as a barrier to entry. J Econ 119(2):17–45
Kreps DM, Scheinkman JA (1983) Quantity precommitment and bertrand competition yield cournot outcomes. Bell J Econ 14(2):326–337
Maggi G (1996) Strategic trade policy with endogenous mode of competition. Am Econ Rev 86(1):237–258
Mendi P (2009) Backward integration and collusion in a duopoly model with asymmetric costs. J Econ 96(2):95–112
Milgrom P, Roberts J (1990) The economics of modern manufacturing: technology, strategy, and organization. Am Econ Rev 80(3):511–528
Nakamura E, Zerom D (2010) Accounting for incomplete pass-through. Rev Econ Stud 77(3):1192–1230
Rey P, Vergé T (2004) Bilateral control with vertical contracts. RAND J Econ 35(4):728–756
Spengler JJ (1950) Vertical integration and antitrust policy. J Polit Econ 58(4):347–352
Villas-Bora SB (2007) Vertical relationships between manufacturers and retailers: inference with limited data. Rev Econ Stud 74(2):625–652
Weyl EG, Fabinger M (2009) Pass-through as an economic tool: principles of incidence under imperfect competition. University of Chicago, Chicago
Weyl EG, Fabinger M (2013) Pass-through as an economic tool: principles of incidence under imperfect competition. J Polit Econ 121(3):528–583
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Proposition 1
Downstream firm i maximizes aggregate profits, given by \(\pi ^{i}=p^{i}q^{i}-TC_q^i -TC_k^i\), by setting price and capacity. With respect to \(TC_q^i\), if the firm produces at or below the capacity, the marginal cost is \(\omega ;\) if the firm produces beyond capacity, marginal cost increases to \(\omega +\theta \). That is, in the price stage, \(TC_q^i\) is:
and \(TC_k^i =\psi q^{i}\). There is a disincentive to produce beyond capacity because of the unfavorable change of marginal cost. In this way, it is possible for firms to sustain a price above the marginal cost in spite of competing in prices. Hence, capacity choice can be used strategically to soften competition in the market stage because there is a difference between “short-run” and “long-run” marginal costs. If firms produce at their capacity, as happens in equilibrium, the profit function becomes \(\pi ^{i}=\left( {p^{i}-\psi -\omega } \right) q^{i}\).
In the second stage, firms engage in Bertrand competition given the capacities that have been decided upon. The Bertrand response functions are the solutions to \(argmax_{p^{i}} p^{i}q^{i}-TC_q^i, i=1, 2:\)
where \(x^{i}=\omega \) for \(q^{i}\le k^{i}\) and \(x^{i}=\omega +\theta \) for \(q^{i}>k^{i}\). Equation (7) defines firm i’s best response to the price charged by firm j. Notice that the best response function “jumps” when output reaches capacity.
Equation (7) defines firms’ best responses dependent on capacity and the price set by the other firms. To find the reaction functions, define the prices for firm i, which ensures that the firm produces exactly at its capacity, \(k^{i}\), given the price charged by firm \(j, p^{j};\) that is \({\Phi }^{i}\left( {p^{j},k^{i}} \right) =\left( {a+dp^{j}-D^{-1}k^{i}} \right) \). Suppose that \({\Phi }^{i}\left( {p^{j},k^{i}} \right) <r^{i}\left( {p^{j},x^{i}} \right) \), that is, the price firm i ideally likes to set is in excess of the price which just makes sure that the firm utilizes capacity. In other words, the marginal-revenue curve of firm i cuts the marginal-cost curve given by \(\omega \) for \(q^{i}\le k^{i}\). This is clearly feasible and the firm’s reaction function is:
In the intermediate case, firm \(i^{\prime }\hbox {s}\) marginal-revenue curve cuts the marginal-cost curve where marginal costs jump from \(\omega \) to \(\omega +\theta \). That is, the firm ideally sets a price that results in production at the capacity limit. Clearly, it can charge a higher price and produce less, or it can charge a lower price and sell more. That is, \(r^{i}\left( {p^{j},\omega +\theta } \right)>{\Phi }^{i}\left( {p^{j},k^{i}} \right) >r^{i}\left( {p^{j},\omega } \right) \). In this situation, the firm sets a price given by \({\Phi }^{i}\left( {p^{j},k^{i}} \right) \), hence the reaction function is:
Finally, consider the parameter configuration that satisfies \({\Phi }^{i}\left( {p^{j},k^{i}} \right) >r^{i}\left( {p^{j},\omega +\theta } \right) \), that is, firm \(i^{\prime }\hbox {s}\) marginal-revenue curve cuts the marginal-cost curve given by \(\omega +\theta \) for some output in excess of capacity, \(q^{i}\ge k^{i}\). Thus, the firm’s reaction function is:
All in all, we have:
Clearly, the reaction-functions’ slopes lie in the range ]0, 1] and is why the price sub-game allows for equilibrium in pure strategies. Thus, Proposition 1 in Maggi (1996) applies. \(\square \)
Proof of Proposition 2
Consider the case where the marginal cost is strictly higher than \(\hat{\omega } -\left( {\theta -\psi } \right) \), but lower than \(\hat{\omega }\), meaning that the marginal cost equals \(MR^{b}\) as well as \(MR^{c}:\) one that induces Cournot competition among downstream duopolistic firms and one that results in Bertrand competition among the downstream duopolistic firms.
When there is Bertrand competition in the downstream duopoly, we can write the first-order conditions for maximizing profit as \(\psi =a-\theta -\left( {1+d} \right) Q^{b}\), or:
Similarly, for Cournot competition in the downstream duopoly, \(\upsilon =a-\psi -\left( {2+d} \right) Q^{c}\), or:
This allows us to write the monopolist’s profits as \(\pi ^{b}=1/2\left( {1+d} \right) \left( {2-d} \right) Q^{{b}^{2}}\) and \(\pi ^{c}=1/2\left( {2+d} \right) Q^{{c}^{2}}\), respectively. It is straightforward that \(\pi ^{c} \gtrless \pi ^{b}\) when:
Using that \(Q^{c}=2\left( {2+d} \right) ^{-1}\left( {a-\psi -\omega } \right) \) and \(Q^{b}=2\left( {\left( {1+d} \right) \left( {2-d} \right) } \right) ^{-1}\left( {a-\theta -\omega } \right) \), this condition becomes:
Now, the profit-maximizing input price is \(\omega ^{c}=1/2\left( {a-\psi +\upsilon } \right) \) when there is Cournot competition among the downstream duopolists, and \(\omega ^{b}=1/2\left( {a-\psi +\theta } \right) \) when there is Bertrand competition among the downstream duopolists. Using this we have:
where \(\sqrt{.}=\sqrt{\left( {2+d} \right) \left( {\left( {1+d} \right) \left( {2-d} \right) } \right) ^{-1}}\). The right-hand side is decreasing in \(\psi \).
Equation (15) is, of course, \(\pi ^{c}-\pi ^{b}\gtrless 0\) and the left-hand side is increasing in \(\upsilon \).
First, take \(\upsilon =\hat{\omega }\) and consider the following variant of Eq. (15):
Using Eq. (4) and rewriting this simplifies to:
or:
which is satisfied. Hence, \(\tilde{\upsilon } \rightarrow \hat{\omega }\) implies \(\pi ^{c}>\pi ^{b}\).
Second, take the lowest feasible value of \(\psi \), that is \(\psi =\omega \left( {\hat{\theta }} \right) -\left( {\hat{\theta } -c_0} \right) \). Using this, consider the following variant of Eq. (15):
or:
Some straightforward manipulation gives:
which is satisfied. Hence, \(\tilde{\psi } \rightarrow \omega \left( {\hat{\theta }} \right) -\left( {\hat{\theta } -c_0} \right) \) implies \(\pi ^{c}<\pi ^{b}\). \(\square \)
Rights and permissions
About this article
Cite this article
Vetter, H. Pricing and market conduct in a vertical relationship. J Econ 121, 239–253 (2017). https://doi.org/10.1007/s00712-017-0529-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-017-0529-5