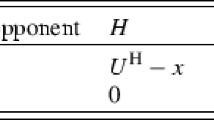
Abstract
The Routh–Hurwitz stability condition is disentangled for choice variables that are strategic substitutes or strategic complements. This yields distinct stability conditions that are not necessarily symmetric. Two examples illustrate this result.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
Note that the situation in panel a corresponds to a value of \(\theta \) that is quite unlikely to be observed. However, the figure only serves to illustrate the workings of the myopic adjustment process underlying (1).
Note that this corresponds to the condition that the absolute value of the slope of the quantity reaction function (9) is less than one.
Strictly speaking, \(x\) is not the ‘level of R&D’ if ‘level’ refers to an investment, although much of the related literature refers to \(x\) in this way. The R&D investment is \(\gamma x^{2}/2\) which yields a reduction in marginal cost of \(x\). The R&D process itself is thus the transformation of \( \gamma x^{2}/2\) into \(x\) (see also Hinloopen 2003).
Qiu (1997) generalizes d’Aspremont and Jacquemin (1988) by allowing products to be differentiated, as in (8), whereby \(\theta \in [0,1]\) and \(b=1\). He takes into account the Routh–Hurwitz stability condition, but considers the case of R&D as a strategic complement only (which applies if \( \beta >\theta /2\)). This yields as stability condition: \((2-\theta \beta )(1+\beta )<\gamma (2+\theta )(4-\theta ^{2})/2\). Qiu (1997) neglects the stability condition in case R&D is a strategic substitute: \((2-\theta \beta )(1-\beta )<\gamma (2-\theta )(4-\theta ^{2})/2\). But this condition is more binding when \(\beta <\theta /2\), that is, when R&D is a strategic substitute. In fact, the claim of Qiu (1997) in his Lemma 1 that his condition A1 (\(\gamma >a/A>1\)) ‘is sufficient but not necessary’ to guarantee stability is not true. For \(\theta >0.8\) and sufficiently small \( \beta \), the relevant stability condition (that is, the condition in case R&D is a strategic substitute) requires \(\gamma \) to be distinguishably larger than \(1\), with the maximum approaching \(\frac{4}{3}\) for \(\beta =0\) and \(\theta \uparrow 1\).
References
d’Aspremont C, Jacquemin A (1988) Cooperative and noncooperative R&D in duopoly with spillovers. Am Econ Rev 78:1133–1137
Bowley AL (1924) The mathematical ground work of economics: an introductory treatise. Clarendon Press, Oxford
Bulow J, Geanakoplos J, Klemperer P (1985) Multimarket oligopoly: strategic substitutes and complements. J Polit Econ 93:488–511
De Bondt R (1997) Spillovers and innovative activities. Int J Ind Org 15:1–28
Dixit A (1986) Comparative statics for oligopoly. Int Econ Rev 27:107–122
Hinloopen J (2003) R&D efficiency gains due to cooperation. J Econ 80:107–125
Martin S (2002) Advanced industrial economics. Blackwell Publishers, Malden/Oxford
Qiu L (1997) On the dynamic efficieny of Bertrand and Cournot equilibria. J Econ Theory 75:213–229
Seade J (1980) On the effects of entry. Econometrica 48:479–489
Acknowledgments
Thanks are due to Stephen Martin and Jan Vandekerckhove for inspiring yet stable discussions. The comments of an anonymous are greatly acknowledged. The usual disclaimer applies.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hinloopen, J. Stability, strategic substitutes, strategic complements. J Econ 116, 129–135 (2015). https://doi.org/10.1007/s00712-014-0422-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-014-0422-4