Abstract
This paper studies a model in which an agent considers proposing a project of unknown quality to an evaluator, who has to decide on whether or not to accept it. Earlier papers considered the case when the evaluation is perfect and showed than higher submission fees increase the expected quality of projects submitted for review by discouraging long-shot submissions. We examine the case of two-sided incomplete information where not only the agent’s, but also the evaluator’s assessment of the project is imperfect. We show that under this specification, an increase in the submission fee may lead to a decrease in the quality of projects that are implemented because of its adverse effects on the evaluator’s acceptance policy.

Similar content being viewed by others
Notes
This fee may be a payment toward the evaluator or a third entity, or it may take a non-monetary form, such as a cost incurred by the agent in terms of time or resources spent on preparing the application or in terms of time by which the evaluator’s decision is delayed.
The optimal fees are not unboundedly high because, in these models, the evaluators need to accept a minimum number of articles. In our paper, we discard this requirement on the evaluator so as to capture situations of project screening beyond that of the academic articles evaluation examined in those papers.
The analysis does not change in a meaningful way if the agent’s payoff also depends on the quality of the project or if the evaluator is also concerned with the quality of projects that he rejects. Since the submission fee may often take a non-monetary form, we do not include it in the evaluator’s payoff.
In the case of an application for economic development in a environmentally sensitive area, both the firm and the regulatory agency can acquire private information through expert analysis about the likelihood that the activity is welfare improving, while, for instance, the firm’s environmental record is public information.
\(c-[ 1-F^{l}( \sigma _{s})] \) is the expected loss from submitting a project of low quality as it is the difference between the submission cost \(c\) and the expected benefit \([ 1-F^{l}( \sigma _{s}) ] \cdot 1\).
We note that there exist values of \(c\) such that \(\mathcal A \)’s equilibrium strategy is interior for any of \(\pi \) and \(L\).
The monotone likelihood property in Assumption 1(ii) implies stochastic dominance.
The formal proof of the fact that \(\frac{c-[ 1-F^{l}\left( \sigma ^{*}\right)] }{[ 1-F^{h}\left( \sigma ^{*}\right)] -c}\) is increasing in \(\sigma ^{*}\), for \(\sigma ^{*}\in \left( \sigma _{1},\sigma _{2}\right) \), is presented in Appendix A2.
In the Appendix, we provide an example of two probability distribution functions \(g^{l}\) and \(g^{h}\) that satisfy Assumption 1 and the conditions \(\lim _{\mu \rightarrow 0}\frac{g^{h}(\mu )}{ g^{l}(\mu )}=0\) and \(\lim _{\mu \rightarrow 1}\frac{g^{h}(\mu )}{ g^{l}(\mu )}=\infty \).
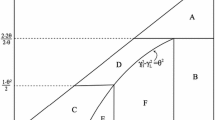
The expected quality of the projects that are implemented is \(l+( h-l) \Pr ( h|\mu \ge \mu ^{*},\sigma \ge \sigma ^{*}) \).
The result of the proposition is a local property that unveils the sign of the effect of a small increase in \(c\) starting from a given equilibrium; it does not elicit a global solution for an optimal submission level. However, in many applications, the submission costs can only be affected marginally.
However, note that this will also lead to fewer projects of both qualities being implemented.
Barbos (2012) shows that this concern is even stronger in models with tiered evaluation.
References
Azar OH (2007) The slowdown in first-response times in economics journals: can it be beneficial? Econ Inq 41:179–187
Barbos A (2012) Project screening with tiered evaluation, working paper, University of South Florida
Boleslavsky R, Cotton C (2011) Learning more by doing less, working paper, University of Miami
Cotton C (2012) On submission fees and response times in academic publishing. Am Econ Rev (forthcoming)
Leslie D (2005) Are delays in academic publishing necessary? Am Econ Rev 95:407–413
Miquel-Florensa J (2010) ‘Tell me what you need’: signaling with limited resources. J Econ 99:1–28
Ottaviani M, Wickelgren A (2009) Approval regulation and learning, with application to timing of merger control, working paper, Northwestern University
Taylor CR, Yildirim H (2011) Subjective performance and the value of blind evaluation. Rev Econ Stud 78:762–794
Acknowledgments
I would like to thank Maciej Dudek, participants at the Fall 2011 Midwest Economic Theory Meetings and SAET 2012, and to two anonymous referees for helpful comments.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Appendix A1. Proof of Lemma 3.1
Consider some arbitrary strategy \(\Lambda ^{ag}\) of \(\mathcal A \). Then, for \(\mathcal E \)’s beliefs, by Bayes’ Rule we have
where \(j(\cdot |\cdot )\) denotes the conditional probability density function of the relevant continuous random variable. Since \(\mathcal A \)’s action and the signal \(\sigma \) are conditionally independent, it follows that
Since the last term in (8) is increasing in \(\frac{f^{h}(\sigma )}{f^{l}(\sigma )}\), the fact that\(\frac{d}{d\sigma }\left[ \frac{ f^{h}(\sigma )}{f^{l}(\sigma )}\right] >0\), as imposed by Assumption 1, implies \(\frac{d}{d\sigma }\Pr (h|\{s\},\sigma )>0\). Thus, given (2), for any \(\Lambda ^{ag}\), \(\mathcal E \) responds with a cutoff strategy by accepting a submitted project if and only if \(\sigma \ge \overline{\sigma }(\Lambda ^{ag})\), with \(\overline{\sigma }(\Lambda ^{ag})\in \left[ 0,1\right] \).
On the other hand, given some arbitrary strategy \(\Lambda ^{ev}\) of \(\mathcal E \), for \(\mathcal A \)’s belief we have
where the second equality follows from the fact that \(\mu \) is redundant for \(\mathcal A \)’s inference about \(\mathcal E \)’s action when conditioning on the quality of the project. Since in any equilibrium \(\mathcal E \) uses a cutoff strategy, we have \(\Pr (\{a\}|h)-\Pr (\{a\}|l)=\Pr (\sigma \ge \overline{\sigma }|h)-\Pr (\sigma \ge \overline{\sigma }|l)=F^{l}(\overline{ \sigma })-F^{h}(\overline{\sigma })\). The monotone likelihood ratio property implies first order stochastic dominance, and thus \(F^{l}(\overline{\sigma } )-F^{h}(\overline{\sigma })>0\). On the other hand, by Bayes’ Rule we have
which is increasing in \(\frac{g^{h}(\mu )}{g^{l}(\mu )}\), and thus increasing in \(\mu \) since \(\frac{d}{d\mu }\left[ \frac{g^{h}(\mu )}{g^{l}(\mu )}\right] >0\) by Assumption 1. Therefore, when \( \mathcal E \) employes a cutoff strategy, \(\frac{d}{d\mu }\Pr (\{a\}|\mu )>0\), and thus \(\mathcal A \)’s best response is a cutoff strategy. \(\square \)
1.2 Appendix A2. Proofs of Lemma 3.2 and Corollary 3.1
(i) Given an arbitrary cutoff strategy \(\sigma _{s}\) of \(\mathcal E \), we have \(\Pr (\{a\}|q)=\Pr (\sigma \ge \sigma _{s}|q)=1-F^{q}\left( \sigma _{s}\right) \), for \(q\in \{h,l\}\). Employing Lemma 3.1 and (10) in \(\Pr (\{a\}|\mu )=\Pr (\{a\}|h)\Pr (h|\mu )+\Pr (\{a\}|l)\Pr (l|\mu )\), it follows that
From (1), we have then that given \(\sigma _{s}\), \(\mathcal A \) submits a project if and only if
Define \(\sigma _{1}^{\prime }\equiv ( F^{l}) ^{-1}\left( 1-c\right) \in \left( 0,1\right) \) and \(\sigma _{2}^{\prime }\equiv ( F^{h}) ^{-1}\left( 1-c\right) \in \left( 0,1\right) \) and note that \( \sigma _{1}^{\prime }<\sigma _{2}^{\prime }\). We have three cases to consider. (i) If \(\sigma _{s}<\sigma _{1}^{\prime }\), then (12) is satisfied for any \(\mu \). To see this, note that \(\sigma _{s}<\sigma _{1}^{\prime }\) implies that \(1-c-F^{l}\left( \sigma _{s}\right) >0\), which together with \(F^{h}\left( \sigma _{s}\right) <F^{l}\left( \sigma _{s}\right) \) implies \(1-c-F^{h}\left( \sigma _{s}\right) >0\), and thus \([ 1-F^{h}\left( \sigma _{s}\right)] -c>0>c-[ 1-F^{l}\left( \sigma _{s}\right)] \). (ii) If \(\sigma _{s}>\sigma _{2}^{\prime }\), then (12) is satisfied for no \(\mu \). To see this, note that \(\sigma _{s}>\sigma _{2}^{\prime }\) implies \(F^{h}\left( \sigma _{s}\right) -1+c>0\), which then implies \(F^{l}\left( \sigma _{s}\right) -1+c>0\), and thus, \([ 1-F^{h}\left( \sigma _{s}\right) ] -c<0<c-[ 1-F^{l}\left( \sigma _{s}\right)] \). (iii) If \(\sigma _{s}\in [ \sigma _{1}^{\prime },\sigma _{2}^{\prime }] \), then note first that \([ 1-F^{h}\left( \sigma _{s}\right)] -c>0\) and \(c-[ 1-F^{l}\left( \sigma _{s}\right)] >0\). By taking the derivative of \(\frac{c-[ 1-F^{l}\left( \sigma _{s}\right)] }{[ 1-F^{h}\left( \sigma _{s}\right)] -c}\) with respect to \(\sigma _{s}\), it follows immediately that this term is increasing in \(\sigma _{s}\) on \([ \sigma _{1}^{\prime },\sigma _{2}^{\prime }] \).
Let \(\overline{S}\equiv \underset{\mu \rightarrow 1}{\lim }\frac{g^{h}(\mu )}{g^{l}(\mu )}\) and \(\underline{S}\equiv \underset{\mu \rightarrow 0}{\lim } \frac{g^{h}(\mu )}{g^{l}(\mu )}\), where \(\{ \overline{S},\underline{S}\} \subset \mathbb R _{+}\cup \{0,+\infty \}\). If \(\overline{S}=\infty \) and \(\underline{S}=0\), then let \(\sigma _{1}\equiv \sigma _{1}^{\prime }\) and \(\sigma _{2}\equiv \sigma _{2}^{\prime }\), and note that as \(\sigma _{s}\) increases from \( \sigma _{1}\) to \(\sigma _{2}\), \(\frac{c-\left[ 1-F^{l}\left( \sigma _{s}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{s}\right) \right] -c}\) increases continuously from \(0\) to \(\infty \). Therefore, for any \(\sigma _{s} \) there exists \(\overline{\mu }\in \left[ 0,1\right] \) such that \(\frac{ g^{h}(\overline{\mu })}{g^{l}(\overline{\mu })}=\left( \frac{c-\left[ 1-F^{l}\left( \sigma _{s}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{s}\right) \right] -c}\right) /\left( \frac{\pi }{1-\pi }\right) \). Assume now that \(\overline{S}<\infty \) and \(\underline{S}>0\). Let \(\sigma _{1}\) be defined implicitly by \(\underline{S}=\left( \frac{c-\left[ 1-F^{l}\left( \sigma _{1}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{1}\right) \right] -c}\right) /\left( \frac{\pi }{1-\pi }\right) \), and \(\sigma _{2}\) be defined implicitly by \(\overline{S}=\left( \frac{c-\left[ 1-F^{l}\left( \sigma _{2}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{2}\right) \right] -c}\right) /\left( \frac{\pi }{1-\pi }\right) \). Note that since \(\lim _{ \sigma _{s}\rightarrow \sigma _{1}^{\prime +}}\frac{c-[ 1-F^{l}\left( \sigma _{s}\right)] }{[ 1-F^{h}\left( \sigma _{s}\right)] -c}=0\) and \(\lim _{\sigma _{s}\rightarrow \sigma _{2}^{\prime -}}\frac{c-\left[ 1-F^{l}\left( \sigma _{s}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{s}\right) \right] -c}=\infty \), we have \(\sigma _{1}>\sigma _{1}^{\prime }\) and \(\sigma _{2}<\sigma _{2}^{\prime }\). Since \(\left[ \sigma _{1}^{\prime },\sigma _{2}^{\prime } \right] \subset \left( 0,1\right) \) and \(\sigma _{1}<\) \(\sigma _{2}\), it follows that \(\left[ \sigma _{1},\sigma _{2}\right] \subset \left( 0,1\right) \). Then, when \(\sigma _{s}\) increases from \(\sigma _{1}\) to \( \sigma _{2}\), \(\left( \frac{c-\left[ 1-F^{l}\left( \sigma _{s}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{s}\right) \right] -c}\right) /\left( \frac{ \pi }{1-\pi }\right) \) increases continuously from \(\underline{S}\) to \( \overline{S}\). Therefore, for any \(\sigma _{s}\in \left[ \sigma _{1},\sigma _{2}\right] \) there exists \(\overline{\mu }\in \left[ 0,1\right] \) such that \(\frac{g^{h}(\overline{\mu })}{g^{l}(\overline{\mu })}=\left( \frac{c-\left[ 1-F^{l}\left( \sigma _{s}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{s}\right) \right] -c}\right) /\left( \frac{\pi }{1-\pi }\right) \). Finally, if \(\overline{S}<\infty \) and \(\underline{S}=0\), then let \(\sigma _{1}\equiv \sigma _{1}^{\prime }\) and \(\sigma _{2}\) be defined implicitly by \(\overline{S}=\left( \frac{c-\left[ 1-F^{l}\left( \sigma _{2}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{2}\right) \right] -c}\right) /\left( \frac{ \pi }{1-\pi }\right) \), while if \(\overline{S}=\infty \) and \(\underline{S}>0\), then let \(\sigma _{1}\) be defined implicitly by \(\underline{S}=\left( \frac{c-\left[ 1-F^{l}\left( \sigma _{1}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{1}\right) \right] -c}\right) /\left( \frac{\pi }{ 1-\pi }\right) \) and \(\sigma _{2}\equiv \sigma _{2}^{\prime }\).
(ii) For the evaluator, from (2) and (8) it follows that, given an arbitrary cutoff strategy \(\mu _{s}\),
We will show next that \(\frac{1-G^{h}(\mu _{s})}{1-G^{l}(\mu _{s})}\) is strictly increasing in \(\mu _{s}\). Thus, computing the derivative, we have
To show that this derivative is positive, note that \(\frac{d}{d\mu }[ \frac{g^{h}(\mu )}{g^{l}(\mu )}] >0\) implies \(\frac{g^{h}\left( \mu _{s}\right) }{g^{l}\left( \mu _{s}\right) }\le \frac{g^{h}\left( x\right) }{ g^{l}\left( x\right) }\) for \(x\in [ \mu _{s},1] \), and thus that \( g^{h}\left( \mu _{s}\right) g^{l}\left( x\right) \le g^{l}\left( \mu _{s}\right) g^{h}\left( x\right) \). Integrating this inequality with respect to \(x\) between \(\mu _{s}\) and \(1\), we obtain \(g^{h}\left( \mu _{s}\right) [ 1-G^{l}\left( \mu _{s}\right) ] \le g^{l}\left( \mu _{s}\right) [ 1-G^{h}\left( \mu _{s}\right)] \) which immediately proves the result. Thus, \(\frac{1-G^{h}(\mu _{s})}{1-G^{l}(\mu _{s})}\) attains its minimum at \(\mu _{s}=0\), and its supremum at \(\mu _{s}=1\).
Now, first, depending on whether the equation \(\frac{\pi }{1-\pi }\lim _{\sigma \rightarrow 1}\frac{f^{h}(\sigma )}{f^{l}(\sigma )}\frac{1-G^{h}(\mu _{s})}{1-G^{l}(\mu _{s})}=L\) has a solution, we have three cases to consider. (i) If \(\frac{\pi }{1-\pi }\lim _{\sigma \rightarrow 1}\frac{f^{h}(\sigma )}{f^{l}(\sigma )}\overline{S}<L\), then condition (13) is not satisfied for any pair \(\left( \sigma ,\mu _{s}\right) \), and thus \(\overline{\sigma }\left( \mu _{s}\right) =1\) for all \(\mu _{s}\in \left[ 0,1\right] \) (here we used l’Hospital Rule to infer that \(\lim _{\mu _{s}\rightarrow 1}\frac{ 1-G^{h}(\mu _{s})}{1-G^{l}(\mu _{s})}=\overline{S}\), and the fact that \( \frac{1-G^{h}(\mu _{s})}{1-G^{l}(\mu _{s})}\) is strictly increasing in \(\mu _{s}\)). In this case, \(\mathcal E \) always exerts full project screening, so \(\mu _{1}\equiv 1\). (ii) If there exists \(\mu ^{\prime }\in \left[ 0,1\right] \) such that \(\frac{\pi }{1-\pi }\lim _{\sigma \rightarrow 1}\frac{f^{h}(\sigma )}{f^{l}(\sigma )}\frac{1-G^{h}(\mu ^{\prime })}{ 1-G^{l}(\mu ^{\prime })}=L\), then condition (13) is not satisfied for pairs \(\left( \sigma ,\mu _{s}\right) \) with \(\mu _{s}<\mu ^{\prime }\), and thus \(\overline{\sigma }\left( \mu _{s}\right) =1\) for \( \mu _{s}\in [ 0,\mu ^{\prime }] \). In this case, \(\mathcal E \) exerts full project screening if and only if \(\mu _{s}\le \mu ^{\prime }\), so \(\mu _{1}\equiv \mu ^{\prime }\). (iii) If \(\frac{\pi }{1-\pi } \lim _{\sigma \rightarrow 1}\frac{f^{h}(\sigma )}{f^{l}(\sigma )} >L \), then \(\mu _{1}\equiv 0\), implying that \(\mathcal E \) never best responds by exerting full project screening.
Second, depending on whether the equation \(\frac{\pi }{1-\pi }\lim _{ \sigma \rightarrow 0}\frac{f^{h}(\sigma )}{f^{l}(\sigma )}\frac{ 1-G^{h}(\mu _{s})}{1-G^{l}(\mu _{s})}=L\) has a solution, we have again three cases to consider. (i) If \(\frac{\pi }{1-\pi }\lim _{\sigma \rightarrow 0}\frac{f^{h}(\sigma )}{f^{l}(\sigma )}\frac{1-G^{h}(0)}{ 1-G^{l}(0)}>L\), then (13) is satisfied for all pairs \( \left( \sigma ,\mu _{s}\right) \), and thus \(\overline{\sigma }\left( \mu _{s}\right) =0\) for all \(\mu _{s}\in [ 0,1] \). In this case, \( \mathcal E \) never exerts any project screening, so \(\mu _{2}\equiv 0\). (ii) If \(\frac{\pi }{1-\pi }\lim _{\sigma \rightarrow 0} \frac{f^{h}(\sigma )}{f^{l}(\sigma )}\frac{1-G^{h}(\mu ^{\prime \prime })}{ 1-G^{l}(\mu ^{\prime \prime })}=L\) for some \(\mu ^{\prime \prime }\in \left[ 0,1\right] \), then (13) is satisfied for all pairs \( \left( \sigma ,\mu _{s}\right) \) with \(\sigma =0\) and \(\mu _{s}\ge \mu ^{\prime \prime }\), and thus \(\overline{\sigma }\left( \mu _{s}\right) =0\) for \(\mu _{s}\in [ \mu ^{\prime \prime },1] \). In this case, \( \mathcal E \) does not exert any project screening when \(\mu _{s}\ge \mu ^{\prime \prime }\), so \(\mu _{2}\equiv 0\). (iii) If \(\frac{\pi }{ 1-\pi }\lim _{\sigma \rightarrow 0}\frac{f^{h}(\sigma )}{ f^{l}(\sigma )}<L\), then \(\mu _{2}\equiv 1\), implying that \(\mathcal E \) always best responds by exerting some project screening. Finally, it is straightforward to see that \(\mu _{1}\le \mu _{2}\) which completes the proof of the Lemma 3.2.
Now, to show Corollary 3.1, note that \(\mathcal A \)’s best-response function \(\overline{\mu }\left( \sigma _{s}\right) \), as elicited from (3), is increasing because \(\frac{d}{d\mu }\left[ \frac{g^{h}(\mu )}{g^{l}(\mu )}\right] >0\) and \(\frac{c-\left[ 1-F^{l}\left( \sigma _{s}\right) \right] }{\left[ 1-F^{h}\left( \sigma _{s}\right) \right] -c}\) is increasing in \(\sigma _{s}\). Second, \(\overline{\sigma }\left( \mu _{s}\right) \) is strictly decreasing since \(\frac{d}{d\sigma }\left[ \frac{f^{h}(\sigma )}{f^{l}(\sigma )}\right] >0\) and \(\frac{\partial }{\partial \mu _{s}}\left[ \frac{1-G^{h}(\mu _{s})}{ 1-G^{l}(\mu _{s})}\right] >0\). \(\square \)
1.3 Appendix A3. Proofs of Proposition 1 and Corollary 3.2
Define \(\sigma _{3}\equiv \overline{\sigma }\left( 0\right) \) and \(\sigma _{4}\equiv \overline{\sigma }\left( 1\right) \). Note that \(\sigma _{3}\) is the upper bound on the set of possible screening standards that \(\mathcal E \) needs to impose in response to strategies employed by \(\mathcal A \), while \(\sigma _{4}\) is the lower bound on that set. It is straightforward to see that both \(\sigma _{3}\) and \(\sigma _{4}\) are weakly increasing in \(L\) and weakly decreasing in \(\pi \).
Now, if \(\sigma _{3}=0\), then it follows then that the only equilibrium of the game is \((\sigma ^{*}=0,\mu ^{*}=0)\). To see this note that when \(\sigma _{3}=0\), \(\mathcal E \) is better off accepting any project even if \( \mathcal A \) exerts no self-screening, and therefore it must be that in equilibrium \(\sigma ^{*}=0\). \(\mathcal A \)’s best response to this strategy of \(\mathcal E \) is to exert no self-screening, and thus \(\mu ^{*}=0\). On the other hand, if \(\sigma _{4}=1\), then the only equilbrium is \((\sigma ^{*}=1,\mu ^{*}=1)\). This is because \(\sigma _{4}=1\) implies that \(\mathcal E \) is better off rejecting any project even if \(\mathcal A \) exerts almost full self-screening. Therefore, it must be that \(\sigma ^{*}=1\), to which \(\mathcal A \)’s best response is to exert full self-screening, and thus \(\mu ^{*}=1\). Note also that \(\sigma _{3}=0\), and thus \(\sigma ^{*}=0\), when \(L\) is sufficiently low and \(\pi \) is sufficiently high, and that \(\sigma _{4}=1\), and thus \(\sigma ^{*}=1\), when \(L\) is sufficiently high and \(\pi \) is sufficiently low. These prove Corollary 3.2(ii). Next, we analyze the case when \(\sigma _{3}>0\) and \(\sigma _{4}<1\).
Thus \(\overline{\sigma }\left( \mu _{s}\right) \), as defined implicitly by (4) decreases (strictly) on \(\left[ 0,1\right] \) from \(\sigma _{3} \) to \(\sigma _{4}\). Define the inverse \(\overline{\sigma }^{-1}:\left[ \sigma _{4},\sigma _{3}\right] \rightarrow \left[ 0,1\right] \), and note that it is decreasing and bijective on its domain. Assume first that \(\sigma _{1}<\sigma _{3}\) and \(\sigma _{4}<\sigma _{2}\). Then \(\overline{\sigma } ^{-1}\left( \sigma _{s}\right) \) and \(\overline{\mu }\left( \sigma _{s}\right) \) must be equal at some value \(\sigma ^{*}\in \left( \max (\sigma _{1},\sigma _{4}),\min (\sigma _{2},\sigma _{3})\right) \). Let \(\mu ^{*}\equiv \overline{\mu }\left( \sigma ^{*}\right) \), and note that \(\sigma ^{*}=\overline{\sigma }\left( \overline{\sigma }^{-1}\left( \mu ^{*}\right) \right) =\overline{\sigma }\left( \overline{\mu }\left( \sigma ^{*}\right) \right) =\overline{\sigma }\left( \mu ^{*}\right) \). Thus, we conclude that \(\left( \mu ^{*},\sigma ^{*}\right) \) as defined is the unique equilibrium of the game. Moreover, since \(\overline{ \sigma }^{-1}\left( \cdot \right) \) is strictly decreasing on \(\left[ 0,1\right] \), we must have \(\mu ^{*}\in (0,1)\) and \(\sigma ^{*}\in \left( 0,1\right) \).
Now, if \(\sigma _{1}\ge \sigma _{3}\), since \(\overline{\mu }(\sigma _{s})=0\) for \(\sigma _{s}\le \sigma _{1}\), and \(\overline{\sigma }(0)=\sigma _{3}\), it follows that the equilibrium is \(\mu ^{*}=0\) and \(\sigma ^{*}=\sigma _{3}\). Note that \(\sigma _{1}\) is decreasing in \(c\), while \(\sigma _{3}\) is increasing in \(L\) and decreasing in \(\pi \). Therefore, as Corollary 3.2(i) states, \(\mu ^{*}=0\) occurs when \(c\) and \(L\) are sufficiently low and when \(\pi \) is sufficiently high. On the other hand, if \(\sigma _{4}\ge \sigma _{2}\), since \(\overline{ \mu }(\sigma _{s})=1\) for \(\sigma _{s}\ge \sigma _{2}\), and \(\overline{ \sigma }(1)=\sigma _{4}\), it follows that then \(\mu ^{*}=1\) and \(\sigma ^{*}=\sigma _{4}\). Since \(\sigma _{2}\) is decreasing in \(c\) and \(\sigma _{4}\) is increasing in \(L\) and decreasing in \(\pi \), \(\mu ^{*}=1\) occurs when \(c\) and \(L\) are sufficiently high and when \(\pi \) is sufficiently low. Therefore, as Corollary 3.2(i) states, \(\mu ^{*}=0\) occurs when \(c\) and \(L\) are sufficiently low and when \(\pi \) is sufficiently high. Note also that it is not possible that \( \sigma _{1}\ge \sigma _{3}\) and \(\sigma _{4}\ge \sigma _{2}\), because these would contradict \(\sigma _{4}<\sigma _{3}\) and \(\sigma _{1}<\sigma _{2} \). Finally, to prove Corollary 3.2(iii), note from the proof of Lemma 3.2(ii) that if \(\frac{\pi }{1-\pi }\lim _{\sigma \rightarrow 1}\frac{f^{h}(\sigma )}{f^{l}(\sigma )}>L\), then \(\mu _{1}=0\), while if \(\frac{\pi }{1-\pi }\lim _{\sigma \rightarrow 0}\frac{f^{h}(\sigma )}{ f^{l}(\sigma )}<L\), then \(\mu _{2}=1\). Thus, when \(\lim _{\sigma \rightarrow 0}\frac{f^{h}(\sigma )}{f^{l}(\sigma )}=0\) and \(\lim _{ \sigma \rightarrow 1}\frac{f^{h}(\sigma )}{f^{l}(\sigma )}=\infty \), these conditions are satisfied, and therefore it must be that \(\sigma ^{*}\in \left( 0,1\right) \). \(\square \)
1.4 Appendix A4.
First, note that
We construct the probability distribution functions \(g^{h},\) \(g^{l}:\left[ 0,1\right] \rightarrow \mathbb R _{+}\) such that \(g^{l}\left( \mu \right) =2-\mu \) for \(\mu \in [ 0,\mu ^{\prime \prime }] \), and \(g^{h}\left( \mu \right) =x\) for \(\mu \in [ \mu ^{\prime },1] \), where \(x\) is a constant and \(\mu ^{\prime \prime }>\mu ^{\prime }\). Then we show that there exists \(\mu _{1}^{\prime },\mu _{2}^{\prime }\) such that condition (14) is satisfied on \([ \mu _{1}^{\prime },\mu _{2}^{\prime }] \subset [ \mu ^{\prime },\mu ^{\prime \prime }] \). We will make sure that \(g^{l}\) is also decreasing on \([ \mu ^{\prime \prime },1] \) and that \(g^{h}\) is increasing on \([ 0,\mu ^{\prime }] \) so that \(\frac{g^{h}(\mu ) }{g^{l}(\mu )}\) is increasing everywhere. Also, we will ensure that both functions are twice continuously differentiable everywhere as also required by Assumption 1. Finally, we will impose that \(g^{l}(1)=0\) and \(g^{h}(0)=0\) so that the limits of \(\frac{g^{h}(\mu )}{g^{l}(\mu )}\) at the boundaries are \(0\) and \(\infty \).
We define \(g^{l}\left( \mu \right) =2-\mu \) for \(\mu \in [ 0,\mu ^{\prime \prime }] \) and then impose the following conditions on \(g^{l} \) on \([ \mu ^{\prime \prime },1] \). First, \(\lim _{\mu \rightarrow \mu ^{\prime \prime +}}g^{l}\left( \mu \right) =2-\mu ^{\prime \prime }\), \(\lim _{\mu \rightarrow \mu ^{\prime \prime +}} \frac{d}{d\mu }g^{l}\left( \mu \right) =-1\) and \(\lim _{\mu \rightarrow \mu ^{\prime \prime +}}\frac{d^{2}}{d\mu ^{2}}g^{l}\left( \mu \right) =0\) so that the function will be twice differentiable at \(\mu ^{\prime \prime }\). Second, \(g^{l}(1)=0\) so that \(\lim _{\mu \rightarrow 1} \frac{g^{h}(\mu )}{g^{l}(\mu )}=\infty \). Finally, we need \(\int _{0}^{1}g^{l}(\mu )d\mu =1\) so that \(g^{l}\) is a proper probability distribution. Since there are five constraints, we define \(g^{l}\) on \([ \mu ^{\prime \prime },1] \) as a polynomial of degree four: \(g^{l}(\mu )\equiv k_{0}+k_{1}\mu +k_{2}\mu ^{2}+k_{3}\mu ^{3}+k_{4}\mu ^{4}\); then, we impose the conditions to obtain a linear system of five equations in the five unknowns, \(k_{0},k_{1},k_{2},k_{3},k_{4}\). Finally, we choose \(\mu ^{\prime \prime }\) so that the resulting function is decreasing on \([ \mu ^{\prime \prime },1] \). The values obtained by solving the linear system for \(\mu ^{\prime \prime }=0.32895\) are: \(k_{0}=2.7699\); \(k_{1}=-8.6738\); \(k_{2}=27.293\); \(k_{3}=-39.71\); \(k_{4}=18.321\).
We employ the same strategy to define \(g^{h}\) on \([ 0,\mu ^{\prime }] \) as a polynomial that satisfies the constraint imposed by Assumption 1 and that ensures that the resulting function \(g^{h}\) is twice continuously differentiable on \(\left[ 0,1\right] \) and that \(g^{h}(0)=0\) and \(g^{h}(1)=1\). Thus, we define \(g^{h}\left( \mu \right) =x\) for \(\mu \in [ \mu ^{\prime },1] \), and then require \(\lim _{ \mu \rightarrow \mu ^{\prime -}}g^{h}\left( \mu \right) =x\), \( \lim _{\mu \rightarrow \mu ^{\prime -}}\frac{d}{d\mu }g^{h}\left( \mu \right) =0\) and \(\lim _{\mu \rightarrow \mu ^{\prime -}}\frac{ d^{2}}{d\mu ^{2}}g^{h}\left( \mu \right) =0\). We also need \( \int _{0}^{1}g^{h}(\mu )d\mu =1\), which can be written as \(\int _{0}^{\mu ^{\prime }}g^{h}(\mu )d\mu +x( 1-\mu ^{\prime }) =1\). Finally, \( g^{h}(0)=0\) implies that the polynomial must have the free coefficient equal to zero. \(\mu ^{\prime }\) is chosen so that the resulting function is increasing. Note that there are four restrictions on \(g^{h}\), so there are four degrees of freedom. Since one degree of freedom is offered by the choice of \(x\), the polynomial will be of degree three and thus, \(g^{h}(\mu )=k_{1}^{\prime }\mu +k_{2}^{\prime }\mu ^{2}+k_{3}^{\prime }\mu ^{3}\). Choosing \(\mu ^{\prime }=0.1\), and solving the resulting linear system, we obtain \(k_{1}^{\prime }=30.769\); \(k_{2}^{\prime }=-307.69\); \(k_{3}^{\prime }=1,025.6\); \(x=1.0256\). Thus, \(g^{h}(\mu )=1.0256\) and \(G^{h}\left( \mu \right) =0.07696+1.0256(\mu -0.1)\) for \(\mu \in \left[ 0.1,1\right] \). With these results, (14) becomes
which is straightforward to check that it holds at \(\mu _{1}^{\prime }\equiv \mu ^{\prime }\) and thus also on some interval \([ \mu _{1}^{\prime },\mu _{2}^{\prime }] \) to the right of that value. \(\square \)
Rights and permissions
About this article
Cite this article
Barbos, A. Imperfect evaluation in project screening. J Econ 112, 31–46 (2014). https://doi.org/10.1007/s00712-013-0334-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-013-0334-8