1 Introduction

The extension and inflation of fibrous thick-walled tubes have been treated in different works since this problem finds its application in a variety of engineering research areas. The biomechanics research community has given some attention to such loading of tubular structures because the results can be useful to understand the mechanical behavior of arterial soft tissue [1,2,3,4,5,6,7]. To give an example for the importance of such a research, it is used to model abdominal aortic aneurysms, reported to be responsible for 1-2% of all deaths in industrialized countries [8]. Additionally, and in general, this research is used to predict the development of healthy and unhealthy arterial tissue properties with deformation.

The properties of biological collagenous soft tissue change with time as its constituents change the framework of growth and remodeling processes [9]. Collagen (fibers) is the most abundant protein in mammals, and it is often the main load-resisting constituent in soft tissues. Various types of enzymes degrade collagen fibers, and experiments have shown that this enzymatic degradation process may be slowed down when fibers are mechanically strained [10,11,12,13,14]. This strain stabilization effect has been taken into account in various mechanical modeling works [15,16,17,18,19,20,21]. A detailed review of mechanical modeling works that account for strain-mediated remodeling of collagen fiber is presented in [22].

In this work, we study the inflation and extension of a thick-walled cylinder. The material is taken to consist of an isotropic ground substance reinforced with two mechanically equivalent fibers families which are symmetrically arranged. These fibers undergo a continuous strain-sensitive remodeling process. In this remodeling process, the fibers are dissolved at a rate depending on the stretch of the fiber, i.e., the fiber dissolution rate decreases when the fibers are stretched. The fiber creation rate is taken to be constant. In the strain-mediated remodeling process, the relation between the current local stresses and the deformation depend on both the past deformation as well as the past deformation history of the material. A model that takes these effects into account has been proposed by Demirkoparan et al. [23], which defined a fiber strain energy density function accounting for the Helmholtz free energy of basic fiber entities denoted as proto-fibers, and a so-called fiber survival kernel that defines the changes of the fiber density with deformation. This model has been refined and specialized in works such as Topol et al. [24, 25], Gou et al. [26], Topol et al. [27]. The works show how the specification of the fiber natural configuration affects the development of the fiber density with the development of the deformation [28]. This work gives special attention to a fiber remodeling process in the balance between fiber creation and dissolution. Such a balance is denoted as homeostasis [29], and it is obtained when the loading of the material remains constant for a sufficiently long period of time so that the (deformation history-dependent) fiber dissolution rate has approached a constant value.

At this point, to consider how the involved parameters in the model, and their engagement, affect the outputs is an important analysis for this research since it will provide a better insight into the mechanical model both quantitatively and qualitatively. The application of the sensitivity analysis method develops that knowledge scrutinizing the behavior of the model since it determines how the input parameters interact with the output parameters.

Frey and Patil [30] summarize sensitivity analysis methods into three groups: (i) the difference in log-odds ratio, the automatic differentiation, the break-even analysis, and the nominal range sensitivity analysis are defined as the mathematical approach that corresponds to deterministic models with a predefined number of parameters; (ii) some different charts and visualization tools such as scatter plots and heat maps can be categorized as a graphical approach; (iii) the Sobol method, the Fourier amplitude sensitivity test (FAST) method, the regression analysis, and the Morris method are defined into the statistical approach and run simulation sample-based methods using probabilistic models. The regression and Morris methods are usually used for monotonic models, while the FAST and Sobol methods are used for complex problems with non-linear and non-monotonic behavior.

In recent works [31, 32], we have applied the Sobol and the FAST methods to study the extension, inflation, and torsion of a circular cylindrical tube. In this work, we study the inflation of a thick-walled cylinder that consists of an isotropic ground substance and remodeling fibers. The mechanical properties of the ground substance are taken to be time-independent. These fibers undergo a continuous strain-sensitive remodeling process, creating fibers at a constant rate, and fibers experience a strain-mediated dissolution. The fiber remodeling model has been proposed in the framework by Demirkoparan et al. [23], which has been applied, often in a specialized form, in works such as Topol et al. [24, 25, 28, 33].

In this work, a sensitivity analysis is performed to determine the relationship among the pressure, the axial force, the axial stretch, the inflation of the tube, the material parameters and arrangement of the constituents, and the initial geometry of the cylinder. More in particular, this article is organized as follows: Sect. 2 summarizes the pressure-inflation and axial load relations for a thick-walled cylinder as well as the mechano-sensitive fiber-remodeling process in a homeostatic balance. Section 3 reviews the applied sensitivity analysis method used in this paper, namely, the Sobol method. The input parameters are assumed to be uniformly distributed. Section 4 applies the Sobol method to the problem described in Sect. 2. Moreover, the assessment of the applied sensitivity analysis method is presented in this section. Finally, in Sect. 5 results and possible further research are considered.

2 Thick-walled fibrous hollow cylinder

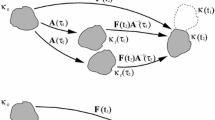
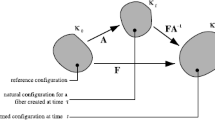
Figure 1 depicts a thick-walled tube, which consists of an isotropic ground substance material and two families of parallel fibers. The fiber families are in a symmetric arrangement with equal mechanical properties. These fibers undergo a remodeling process, which is mediated by a mechanical strain. The material is taken to be incompressible, which is motivated by the water content of biological soft tissue.

Fig. 1
figure 1

Thick-walled cylinder in the reference configuration \(\mathcal {B}_0\) and in the deformed configuration \(\mathcal {B}\). In the reference configuration, the cylinder has the inner and outer radii \(R_i\) and \(R_e\). Due to the application of an inflation pressure P and an axial stretch (that corresponds to the axial force N, the deformed cylinder has the inner and outer radii \(r_i\) and \(r_e\)

Full size image

In the reference configuration \(\mathcal {B}_0\), let \(\left\{ {\textbf{E}}_{r}, {\textbf{E}}_{\theta }, {\textbf{E}}_{z} \right\} \) be three base unit vectors of a cylindrical coordinate system. This configuration is also taken to be the stress-free configuration of the material [34]. In terms of the cylindrical coordinates \(\{R, \Theta , Z\}\), the geometry of the cylinder can be described as

$$\begin{aligned} R_i\le R\le R_e,\qquad 0\le \Theta \le 2\pi ,\qquad -\dfrac{L}{2}\le Z\le \dfrac{L}{2}, \end{aligned}$$
(1)

where \(R_i\), \(R_e\), and L are the inner and outer radii and the length of the cylinder, respectively. The fiber orientations of the fibers for both families are indicated by the two unit vectors

$$\begin{aligned} {\textbf{N}}_1&\;=\;&\cos (\alpha )\;{\textbf{E}}_{\theta }+\sin (\alpha ){\textbf{E}}_{z}, \end{aligned}$$
(2a)
$$\begin{aligned} {\textbf{N}}_2&\;=\;&\cos (\alpha )\;{\textbf{E}}_{\theta }-\sin (\alpha )\;{\textbf{E}}_{z}, \end{aligned}$$
(2b)

where \(\alpha \) is the fiber winding angle that defines the fiber orientation between the fiber direction and the azimuthal direction. Because of the identical mechanical properties of the fibers and the symmetric arrangement of the fibers, internal pressurization of the cylinder leads to inflation without a twist. Although twist-related helical coiling of arterial tissue may lead to severe issues in the functionality of the vessels, such effects are ignored in this article [35].

Let \(\mathcal {B}(t)\) be the deformed configuration at t, for which the cylinder has the inner radius \(r_i=r_i(t)\) and outer radius \(r_e=r_e(t)\). In cylindrical coordinates \((r,\theta ,z)\) of the deformed configuration \(\mathcal {B}(t)\) at time t, the inflation of the cylinder is written as

$$\begin{aligned} r=r(R,t) \qquad \theta =\Theta ,\qquad z=\lambda _z\;Z. \end{aligned}$$
(3)

The deformation gradient tensor \({\textbf{F}}(t)={\textbf{F}}^{(\mathcal {B}_0\rightarrow \mathcal {B}(t))}\) for the deformation \(\mathcal {B}_0\rightarrow \mathcal {B}(t)\) is

$$\begin{aligned} {\textbf{F}}(t)= \lambda _{r}(t)\;{\textbf{E}}_{r}\otimes {\textbf{E}}_{r}+ \lambda (t)\;{\textbf{E}}_{\theta }\otimes {\textbf{E}}_{\theta }+ \lambda _{z}{\textbf{E}}_{z}\otimes {\textbf{E}}_{z}, \end{aligned}$$
(4)

where

$$\begin{aligned} \lambda _r(t)=\dfrac{\text{ d }r(t)}{\text{ d }R}=\dfrac{1}{\lambda (t)\;\lambda _z},\qquad \lambda (t)=\dfrac{r(t)}{R},\qquad \lambda _z=\dfrac{z}{Z} \end{aligned}$$
(5)

are the principal stretches in the radial, circumferential, and axial directions, respectively. The incompressibility constraint \(\text{ det }{\textbf{F}}=\lambda _r\lambda \lambda _z=1\) allows to express the radial stretch in terms of the other two principal stretches, i.e. \( \lambda _r(t)={1}/{\lambda (t)\lambda _z}\).

It follows that the radial location function r(R, t) for the deformed cylinder is given by

$$\begin{aligned} r^2-r_i^2=\lambda _z^{-1}\left[ R^2-R_i^2\right] , \end{aligned}$$
(6)

where \(r_i=r_i(t)=r(R_i,t)\) is the inner radius of the deformed cylinder at time t.

The azimuthal stretches at the inner and outer cylinder walls are

$$\begin{aligned} \lambda _i=\frac{r_i}{R_i},\qquad \lambda _e=\frac{r_e}{R_e}. \end{aligned}$$
(7)

From (6) one obtains the outer cylinder radius \(r_e\), taking \(r=r_e\) and \(R=R_e\), so that the azimuthal wall stretches (7) are related via

$$\begin{aligned} \lambda _e= \sqrt{\dfrac{1}{\lambda _z}\left[ 1-\dfrac{R_i^2}{R_e^2}\right] +\dfrac{R_i^2}{R_e^2}\;\lambda _i^2}. \end{aligned}$$
(8)

The form (4) of the deformation gradient tensor as well as the mechanical and loading symmetries of the system suggest that the Cauchy stress tensor \({\textbf{T}}\) is

$$\begin{aligned} {\textbf{T}}=T_{r}\;{\textbf{E}}_{r}\otimes {\textbf{E}}_{r}+T_{\theta }\;{\textbf{E}}_{\theta }\otimes {\textbf{E}}_{\theta }+T_{z}\;{\textbf{E}}_{z}\otimes {\textbf{E}}_{z}, \end{aligned}$$
(9)

where \(T_{r}\), \(T_{\theta }\), and \(T_{z}\) are the normal stresses in the radial, azimuthal, and axial directions, respectively. For the incompressible material the Cauchy stress tensor and the deformation gradient tensor are related via

$$\begin{aligned} {\textbf{T}}=-p\textbf{I}+2\textbf{F}\frac{\partial {W}}{\partial {\textbf{C}}}\textbf{F}^T, \end{aligned}$$
(10)

in which p is a scalar resulting from the incompressibility constraint, \({\textbf{I}}\) is the second-order identity tensor, \({\textbf{C}}={\textbf{F}}^T{\textbf{F}}\) is the right Cauchy-Green deformation tensor, and W is the strain energy density function that defines the mechanical properties of the material. The three principal Cauchy stress elements are determined via

$$\begin{aligned} T_{r}= & {} -p+\lambda _r \dfrac{\partial W}{\partial \lambda _r},\end{aligned}$$
(11a)
$$\begin{aligned} T_{\theta }= & {} -p+\lambda \dfrac{\partial W}{\partial \lambda },\end{aligned}$$
(11b)
$$\begin{aligned} T_{z}= & {} -p+\lambda _z\dfrac{\partial W}{\partial \lambda _z}. \end{aligned}$$
(11c)

In the modeling of hyperelastic fibrous materials, the strain energy density function is usually decomposed into the contribution of the isotropic ground substance \(W_m\) and the fibers \(W_f\), i.e. \(W=W_m+W_f\). The inflation pressure \(P(t)\ge 0\) acts on the inner cylinder wall, which gives the following boundary conditions for the radial stresses:

$$\begin{aligned} T_{r}&\;=\;&-P\quad \text{ on } \quad r=r_i,\end{aligned}$$
(12a)
$$\begin{aligned} T_{r}&\;=\;&0\quad \text{ on } \quad r=r_e. \end{aligned}$$
(12b)

We now (briefly) obtain the pressure-inflation relation as well as the axial load associated with this boundary value problem in which the axial stretch is considered to be a constant value. For a broader discussion deriving the pressure-inflation relation and the corresponding relation for the axial force in the context of isotropic and anistropic materials applicable to arterial soft tissue modeling, we refer to works such as Ogden [36] and Goriely [37].

Body forces are assumed to be negligible, for which the Cauchy stress tensor \({\textbf{T}}\) fulfills \(\textrm{div}{\textbf{T}}={\textbf{0}}\). This gives

$$\begin{aligned} \dfrac{\textrm{d}T_{r}}{\textrm{d r}}=\dfrac{T_{\theta }-T_{r}}{r}. \end{aligned}$$
(13)

After integration of (13), one obtains

$$\begin{aligned} \left. T_{r}\right| _{r}-\left. T_{r}\right| _{r_i}=\int _{r_i}^{r}\dfrac{T_{\theta }-T_{r}}{r}\;\textrm{d}r. \end{aligned}$$
(14)

In some cases, it can be convenient to express (14) in terms of stretches instead of the radii. For that reason, Equation (6) can be written as

$$\begin{aligned} r^2\left[ 1-\dfrac{1}{\lambda ^2\lambda _z}\right] =r_i^2-\dfrac{1}{\lambda _z}R_i^2 \end{aligned}$$
(15)

which can be brought into the form

$$\begin{aligned} r =\sqrt{\lambda _z\left[ r_i^2-\dfrac{R_i^2}{\lambda _z}\right] \left[ \dfrac{\lambda ^2}{\lambda ^2\lambda _z-1}\right] }. \end{aligned}$$
(16)

Then the derivative of r in (16) with respect to the azimuthal stretch \(\lambda \) gives

$$\begin{aligned} \begin{array}{lllllll} \dfrac{\text{ d }r}{\text{ d }\lambda } = - \dfrac{\lambda \lambda _z\left[ r_i^2-\dfrac{R_i^2}{\lambda _z}\right] }{\left[ \lambda ^2\lambda _z-1\right] ^2 r}. \end{array} \end{aligned}$$
(17)

Notice that in the numerator of (17), the terms in the bracket are the same ones that are on the right side of (15). After the substitution of the right side of (15) into (17), one obtains

$$\begin{aligned} \dfrac{\text{ d }r}{\text{ d }\lambda } = - \dfrac{r}{\lambda \left[ \lambda ^2\lambda _z-1\right] }. \end{aligned}$$
(18)

Now, (14), after some simple manipulations which include the use of the boundary conditions in (12) and derivative in (18) can be presented in the form

$$\begin{aligned} P=\int _{\lambda _e}^{\lambda _i}\dfrac{1}{\lambda ^2\;\lambda _z-1}\;\dfrac{\partial W}{\partial \lambda }\;\text{ d }\lambda . \end{aligned}$$
(19)

The associated (reduced) axial force can be expressed in terms of the principal stresses as follows (see, e.g. Murphy and Rajagopal [38])

$$\begin{aligned} N=\pi \int _{r_i}^{r_e}\left[ 2T_{z}-T_{r}-T_{\theta }\right] r\;\textrm{d}r. \end{aligned}$$
(20)

With the help of the expression for the Cauchy stress element in (11) and the derivative in (17), Eq. (20) can be brought into the form

$$\begin{aligned} \begin{array}{llll} N&{}=&{}\pi R_i^2\left[ \lambda _{i}^2\lambda _z-1\right] \\ &{}\quad \times &{}\displaystyle \int _{\lambda _{e}}^{\lambda _{i}} \dfrac{\left[ 2\lambda _z\dfrac{\partial W}{\partial \lambda _z}-\lambda _r\dfrac{\partial W}{\partial \lambda _r}-\lambda _{\theta }\dfrac{\partial W}{\partial \lambda }\right] }{\left[ \lambda ^2\lambda _z-1\right] ^2} \lambda \;\textrm{d}\lambda . \end{array} \end{aligned}$$
(21)

It has to be pointed out that the inflation of the cylinder is restricted to the consideration of the stable inflation of the material. Depending on the geometry, the mechanical properties of the material, and the loading conditions, inflated and axially stretched cylinders may neck, bulge, bend, or face various other types of instabilities [39].

2.1 Remodeling fibers in an isotropic ground substance

The strain energy density of the material and material constituents can be expressed as a function of two independent variables \(\lambda \) and \(\lambda _z\), i.e., \(W=\hat{W}(\lambda ,\lambda _z)\), and in what follows we use that notation when variables are given in terms of these two independent variables. The mechanical behavior of the ground substance \(\hat{W}_m(\lambda ,\lambda _z)\equiv W_m\) is taken to be time-independent, and it will be modeled as an incompressible neo-Hookean material, which depends on the first invariant of \({\textbf{C}}\),

$$\begin{aligned} \hat{I}_1=\dfrac{1}{\lambda ^2\;\lambda _z^2}+\lambda ^2+\lambda _z^2. \end{aligned}$$
(22)

For the herein studied deformation of the cylinder, the strain energy density function for the neo-Hookean material can be expressed in terms of the azimuthal and axial stretches,

$$\begin{aligned} \hat{W}_m(\lambda ,\lambda _z)= \dfrac{\mu }{2}\left[ \dfrac{1}{\lambda ^2\;\lambda _z^2}+\lambda ^2+\lambda _z^2-3\right] , \end{aligned}$$
(23)

which has made use of the invariant in (22). Volume changes in the ground substance, that may occur in an incompressible setting, for example, due to inflammation-related swelling processes (see, e.g., Zamani et al. [40], Tsai et al. [41]), can affect both the fiber remodeling process [26, 27] and the stability of the cylinder [42, 43]; such material volume changing processes and the initiation of instabilities are ignored in the framework of this article.

The strain energy density function for the two families of fibers is taken in the form of an integral equation concerning fiber creation time \(\tau \) that has been initially proposed by Demirkoparan et al. [23],

$$\begin{aligned} \begin{array}{lllll} {W}_{f}&{}=&{}\displaystyle \sum _{i=4,6}\int _{-\infty }^t \psi _f(\hat{I}_i)\;\zeta (t,\tau )\;\text{ d }\tau \\ &{}=&{}\displaystyle 2\int _{-\infty }^t \psi _f(\hat{I}_4)\;\zeta (t,\tau )\;\text{ d }\tau , \end{array} \end{aligned}$$
(24)

where \(\hat{I}_4\) and \(\hat{I}_6\) are invariants associated with the fiber stretch of each family which will be introduced shortly, and \(\psi \) is a function. Notice that in Eq. (24) the upper fiber lifespan is theoretically unbounded. For articles that account for a finite upper fiber lifespan in the fiber remodeling process we refer to Topol et al. [28, 33]. The first term in the integrand of Eq. (24) is the Helmholtz free energy of a single proto-fiber,

$$\begin{aligned} \psi _f({\hat{I}}_4)= \left\{ \begin{array}{llllll} \dfrac{\gamma _1}{2\gamma _2}\left[ e^{\gamma _2\left[ {\hat{I}}_4-1\right] ^2}-1\right] &{} \text{ if } {\hat{I}}_4>1,\\ 0&{} \text{ if } {\hat{I}}_4\le 1, \end{array}\right. \end{aligned}$$
(25)

which is taken in an exponential form motivated by the strain stiffening of the fibers [44] and where \(\gamma _1\) (related to the initial stiffness of collagen fibers) and \(\gamma _2\) (related to the stiffening at larger stretches in the strain stiffening of the collagen fibers,) are constants. Furthermore, due to the symmetric arrangement of the fibers and the inflation without twist, the invariants \(\hat{I}_4(\lambda ,\lambda _z)\) and \(\hat{I}_6(\lambda ,\lambda _z)\) are equal and given by

$$\begin{aligned} \hat{I}_4(\lambda ,\lambda _z)=\lambda ^2\cos ^2\alpha +\lambda _z^2\sin ^2\alpha =\hat{I}_6(\lambda ,\lambda _z). \end{aligned}$$
(26)

The form for \(\hat{I}_4(\lambda ,\lambda _z)\) in Eq. (26) is based on the assumption that the ground substance and the fibers share a common stress-free configuration. Here, for convenience, the common stress-free configuration is taken to be the reference configuration \(\mathcal {B}_0\). Fibers are taken to be parallel within their respective fiber families. The invariant \(\hat{I}_4(\lambda ,\lambda _z)\) is interpreted as the squared magnitude of the fiber stretch. For modeling in terms of other (higher) fiber invariants including those with a natural configuration that differs from that of the ground substance, we refer to Topol et al. [45]. Such natural fiber configuration may be constant or vary with the deformation history of the overall material. In the latter case, the fiber natural configuration may depend on the fiber creation time \(\tau \). For example, Topol et al. [24, 25, 46] have shown that the specification of the fiber natural configuration has a signification influence on the relationship between loading and deformation during the remodeling process at hand. While the present modeling assumption takes the unloaded configuration as the stress-free configuration, other modeling works have focused on the role of residual stress [4, 7, 47, 48].

The kernel of the right term in Eq. (24) is the fiber survival kernel that accounts for a change in the fiber density with deformation history [23]

$$\begin{aligned} \zeta (t, \tau )=\chi _c\exp \left( -\int _{\tau }^{t} \eta (\hat{I}_4(\lambda (s),\lambda _z)) \;\text{ d }s\right) \end{aligned}$$
(27)

where \(\chi _c\) is the fiber creation rate that is taken to be constant, and

$$\begin{aligned} \eta (\hat{I}_4)=\left\{ \begin{array}{llllllllll} k_1e^{-k_2\left[ \sqrt{\hat{I}_4}-1\right] }&{} \text{ if } \hat{I}_4\ge 1,\\ k_1&{} \text{ if } \hat{I}_4\le 1, \end{array} \right. \end{aligned}$$
(28)

is the fiber stretch ( i.e.\(\sqrt{\hat{I}_4}\)) dependent dissolution rate function [23]. In the dissolution rate function (28), the parameter \(k_1=\eta (1)>0\) is the fiber dissolution rate for un-stretched fibers and the parameter \(k_2\) in the exponent gives the sensitivity of the dissolution rate to the fiber stretch. Alternative forms for the fiber dissolution rate function have been suggested, for example, in Topol et al. [46].

The integration of just the fiber survival kernel \(\zeta (t, \tau )\) in (27) with respect to the fiber creation time \(\tau \) gives the fiber density function [28, 49],

$$\begin{aligned} \rho =\int _{-\infty }^t\zeta (t, \tau )\;\text{ d }\tau . \end{aligned}$$
(29)

This function allows us to determine the development of the fiber density for a known deformation history regardless of the knowledge of a strain energy density function for the ground substance or the proto-fibers fibers (see, e.g. Topol et al. [28]).

Note that the time-dependent behavior of the material is solely due to the mechano-sensitive remodeling of the fibers. This remodeling process is related to enzymatic fiber degradation, the creation of the fibers, and the strain stabilization of the fibers during the enzymatic degradation. Softening, damage, and failure effects, among others, may occur at larger strains which are not related to the enzymatic remodeling [50, 51] and for that reason they are not (at the moment) part of the herein-considered modeling of the material behavior.

2.2 Homeostasis during fiber remodeling process

Let us assume that after the application of the constant axial stretch \(\lambda _z\) and the constant inflation pressure P (\(=P_h\)) for a sufficiently long period of time, the fiber remodeling process approaches a balance between the fiber creation and the fiber dissolution process. This balance in the dynamic processes is denoted as homeostasis [22]. All parameters that are associated with homeostasis are labeled by an "h" in the subscript, e.g. the invariant in (26) becomes

$$\begin{aligned} \hat{I}_{4,h}(\lambda _h,\lambda _z)=\lambda _h^2\cos ^2\alpha +\lambda _z^2\sin ^2\alpha . \end{aligned}$$
(30)

In a homeostatic fiber remodeling, the dissolution rate function (28) takes the constant value

$$\begin{aligned} \eta _h(\hat{I}_{4,h})=\dfrac{k_1}{e^{k_2\left[ \sqrt{\hat{I}_{4,h}}-1\right] }}, \end{aligned}$$
(31)

for which the fiber survival kernel (27) becomes, after solving the integrals,

$$\begin{aligned} \zeta _h(t, \tau ) =\chi _c\exp \left( \eta _h\tau \right) \exp \left( -\eta _h t\right) . \end{aligned}$$
(32)

After substitution of (23)–(28), (30), (31) into (19), the integrals concerning fiber creation time \(\tau \) in (24) can be solved analytically so that one obtains the pressure-inflation relation (see Topol et al. [33] for details)

$$\begin{aligned} \begin{array}{llllllllllllll} P_h &{}\;=\;&{}\mu \left[ \dfrac{\lambda _{i,h}^2-\lambda _{e,h}^2}{2\lambda _{e,h}^2\;\lambda _{i,h}^2\;\lambda _z^2} +\ln \left( \dfrac{\lambda _{i,h}}{\lambda _{e,h}}\right) \right] \\ &{}&{}+ 4 \gamma _1\chi _c \cos ^2\alpha \displaystyle \int _{\lambda _{e,h}}^{\lambda _{i,h}} \dfrac{\lambda _h}{\lambda ^2_h\;\lambda _z-1} e^{\gamma _2\left[ \lambda _h^2\cos ^2\alpha +\lambda _z^2\sin ^2\alpha - 1\right] ^2}\\ &{}&{}\;\times \;\displaystyle \left[ \lambda _h^2\cos ^2\alpha +\lambda _z^2\sin ^2\alpha - 1\right] \displaystyle \dfrac{e^{k_2\left[ \sqrt{\lambda _h^2\cos ^2\alpha +\lambda _z^2\sin ^2\alpha }-1\right] }}{k_1} \;\text{ d }\lambda _h, \end{array}\nonumber \\ \end{aligned}$$
(33)

where \(\lambda =\lambda _{i,h}\) and \(\lambda =\lambda _{e,h}\) are the azimuthal stretches at the inner and outer surface of the tube, respectively. The first term on the right hand side of (33) results from the neo-Hookean contribution of the ground substance, and the other term results from the contribution of the fibers. It has to be pointed out that if \(\gamma _1=0\), then for \(P\ge \mu \ln (R_e/R_i)\) the cylinder will be subjected to unbounded inflation [52], which is also denoted as an inflation jump instability.

In a similar way, one can derive the axial force \(N=N_{h}\) for a homeostatic fiber remodeling process from (21) in the form

$$\begin{aligned} \begin{array}{lllll} N_h&{}=&{}\pi R_1^2 \left[ \lambda _{i,h}^2\lambda _z - 1\right] \left\{ \mu \Bigg [\dfrac{ \lambda _{e,h}^4 \lambda _z^2 - 2 \lambda _{e,h}^2 \lambda _z^4 + 1}{\lambda _{e,h} \lambda _z^2 (\lambda _{e,h}^2 \lambda _z - 1)^2} - \dfrac{ \lambda _{i,h}^4 \lambda _z^2 - 2 \lambda _{i,h}^2 \lambda _z^4 + 1}{\lambda _{i,h} \lambda _z^2 (\lambda _{i,h}^2 \lambda _z - 1)^2}\Bigg ]\right. \\ &{}&{}\left. +\displaystyle 4 \gamma _1\chi _c \int _{\lambda _{e,h}}^{\lambda _{i,h}} \dfrac{e^{\gamma _2 (\lambda _h^2 \cos ^2\alpha + \lambda _z^2 \sin ^2\alpha - 1)^2}}{(\lambda _h^2 \lambda _z - 1)^2} \left( \lambda _h^2 \cos ^2\alpha + \lambda _z^2 \sin ^2\alpha - 1\right) \right. \\ &{}&{}\left. \times \left( 2\lambda _z^2 \sin ^2\alpha -\lambda _h^2 \cos ^2\alpha \right) \dfrac{e^{k_2\left[ \sqrt{\lambda _h^2\cos ^2\alpha +\lambda _z^2\sin ^2\alpha }-1\right] }}{k_1} \lambda _h \;\text{ d }\lambda _h \right\} . \end{array}\nonumber \\ \end{aligned}$$
(34)

Notice that in both Eqs. (33) and (34), the azimuthal stretches at the outer and inner cylinder wall \(\lambda _{e,h}\) and \(\lambda _{i,h}\) are related via (8).

For the homeostatic balance in the fiber remodeling process the fiber density function (29) can be determined using (30 –31),

$$\begin{aligned} \rho _h=\dfrac{\chi _c}{k_1}e^{k_2\left[ \sqrt{\lambda _h^2\cos ^2\alpha +\lambda _z^2\sin ^2\alpha }-1\right] } \end{aligned}$$
(35)

3 Recap of the applied sensitivity analysis method and its assessment

3.1 Sobol method

To determine the influence of input parameters on output variables in a model, various sensitivity analyses have been applied. These sensitivity analysis methods have different approaches that have been reviewed, for example, by Saltelli et al. [53,54,55].

Recently, we applied some sensitivity analysis methods in order to understand the influence of various parameters in pre-stresses tubular materials that are subjected to a combination of axial extension, inflation by an inner pressure, and torsion [31]. In this article, we apply the Sobol method to the problem introduced in Sect. 2.2. The Sobol method is categorized as a variance-based sensitivity analysis (VBSA). This method is also defined as a numerical method in a statistical approach. The Sobol method evaluates the uncertainty of the model output based on the contribution of uncertainties of input parameters in the model [53]. In other words, the Sobol method considers how much of the variability in a model output depends on individual input parameters or the interaction between involved parameters using variance-based computation [54] without having a hypothesis on the relationship between the input and output of the model [55].

Suppose that the function \(g(\cdot )\) is defined in the interval \({[0,\ 1]}^k\) in the form [53]

$$\begin{aligned} g\left( X\right) =\displaystyle g_0+\sum ^k_{i=1}{g_i\left( X_i\right) } +\displaystyle \sum ^k_{i<j}{g_{ij}(X_i,X_j)}\ +\dots +g_{12\dots k}(X), \end{aligned}$$
(36)

where

$$\begin{aligned} \begin{array}{llllll} \displaystyle \int ^1_0{g_{i_1\dots i_r}\left( X_{i_1},\dots ,X_{i_r}\right) dX_{i_l}=0},\qquad 1\le l\le r,\\[3ex] \{i_1,\ ...,{\ i}_r\}\subseteq \{1,...,k\}, \end{array} \end{aligned}$$
(37)

where \(X=(X_1,..., X_k)\) is a random vector, and g(X) is the output of the model, which is denoted y in what follows. The functional analysis of variance (ANOVA) method [56] is

$$\begin{aligned} \textrm{Var}\left( y\right) =\ \sum ^k_{i=1}{D_i\left( y\right) }+\sum ^k_{i<j}{D_{ij}(y)}+\dots +D_{12\dots k}(y), \end{aligned}$$
(38)

where the first-order of variance for expected value y|x is defined as \(D_i(y)=\textrm{Var}[E(y\ |X_i)]\), while second-order interaction of variance for expected value y|x is defined as \(D_{ij}(y)=\textrm{Var}[E(y\ |X_i,\ X_j)]-D_i(y)-D_j(y)\). Similarly, higher-order interaction terms can be obtained. Hence, the first-order Sobol index and second-order interaction index [57] are, respectively, as follows:

$$\begin{aligned} Sy_i=\dfrac{D_i(y)}{\textrm{Var}(y)},\qquad S_{ij} =\dfrac{D_{ij}(y)}{\textrm{Var}(y)}, \end{aligned}$$
(39)

which has \(2^k-1\) indices. Archer et al. [58] proposed the following total Sobol indices

$$\begin{aligned} S_{T_i}=Sy_i+\sum _{i<j}{S_{ij}}+\sum _{j\ne i,l\ne i,j<q}{S_{ijq}}+\dots =\sum _{q\in \#i}{S_q}, \end{aligned}$$
(40)

where \(\#i\) considers all the subsets of 1, ..., k that include the index i. To obtain the Sobol indices in the model a sampling design and an estimator are required. For sampling design, Monte Carlo sampling-based methods were proposed by Sobol [59], and subsequently, they have been developed for both the first-order and total indices by Saltelli [57]. Using the application of the Monte Carlo method, the error estimation for the Sobol indices is gained using asymptotic formulas [60], bootstrap methods [58], and random repetition [61]. On the other hand, there are some estimators to obtain the first order and the total effect of Sobol indices. In this work, we apply two important estimators: “Saltelli estimator" for first-order effect [62] and the “Janson estimator" for total sensitivity indices [63], both by means of statistical simulation in “R" program. These estimators have been proposed by Puy et al. [64] and Saltelli et al. [62] and are used for non-monotonic and non-linear models, as it is the case at hand.

The Saltelli estimator for first-order indices is

$$\begin{aligned} S_{i} = \frac{{\frac{1}{k}\sum \nolimits _{{j = 1}}^{k} {g\left( B \right) _{j} } \left[ {g\left( {A_{B}^{{\left( i \right) }} } \right) _{j} - g\left( A \right) _{j} } \right] }}{{{\text {Var}}(y)}}, \end{aligned}$$
(41)

which relies on specific combinations for the matrices \(A,\ B,\) and \(A^{\left( i\right) }_B\).In these matrices, each row is a sampling point and each column represents a model input. Any sampling point in matrices is \(X_{j,i}\), where i represents the column (from 1 to k) and j illustrates the index of the row (from 1 to N). For further explanations of these matrices we refer to Puy et al. [64]. For total Sobol indices, the Janson estimator is given by

$$\begin{aligned} T_{i} = \frac{{\frac{1}{{2k}}\sum \nolimits _{{j = 1}}^{k} {\left[ {g\left( A \right) _{j} - g\left( {A_{B}^{{\left( i \right) }} } \right) _{j} } \right] ^{2} } }}{{{\text {Var}}(y)}}. \end{aligned}$$
(42)

The Saltelli-Janson estimators are used together with a sample-based approach. Moreover, one can use \(T_i-S_i\) as a measure for the interpretation of Sobol indices (i.e. what this measure means for individual input variables) and describe how much the uncertainties of a model can be described by the higher-order interaction effect of \(X_i\) with other input factors. An input parameter, such as \(X_i\), does not have any effect if and only if \(T_i = 0\), and this parameter can be considered a constant and not a variant for the model output [63].

The “Saltelli-Jansen” estimators in the Sobol method are applied using the uniform distribution for the input parameters introduced in Sect. 2. Statistical simulations are conducted in the “R" programming considering the probability distribution instead of deterministic fixed data or just random data for possible values of input variables [54].

Second-order interactions defined in Eq. (39) are obtained using Liu and Owen’s formula [65] that gives higher-order interaction between two input parameters on the model output. In particular, second-order interactions are estimated as

$$\begin{aligned} \begin{array}{llllllllllll} \hat{S}_{i,j}&{}=&{}\displaystyle \dfrac{1}{4n} \sum ^n_{k=1} \Big (f(X_i^k,X_j^k,X^k_{-{i,j}} ) -f(X_i^k,P_j^k,X^k_{-{i,j}} )\\[3ex] &{}&{}-f(P_i^k,X_j^k,X^k_{-{i,j}}) +f(P_i^k,P_j^k,X^k_{-{i,j}})\Big )^2, \end{array} \end{aligned}$$
(43)

where \(P_i\) and \(P_j\) are two independent copies defined on the interval \({[0,\ 1]}^m\) from \(X_i\) and \(X_j\), respectively, n is the sample size of input parameters and k is the number of repetitions in model output. In (43), \(X_{-{i,j}}\) describes the interaction effect of two input parameters without the direct effect for \(X_{i,j}\) parameters. In other words, (43) is the estimation of the expected values of the joint effects of two input parameters on the output of the model. We illustrate the results of the joint effects of input parameters on model outputs using a scatter plot matrix. Scatter plots for the three most sensitive parameters on both pressure and axial force formulas are obtained in what follows. In all these cases, the scatter plots are shown for the corresponding domain associated with each input parameter since we are working with the uniform distribution and these values have physical meaning.

Now, Sect. 3.2 gives a brief description of the uniform distribution. Also, in Sect. 3.3, the bias and standard deviation measures used as assessment measurements for Sobol indices are presented.

3.2 Definition of applied probability distribution in the sensitivity analysis

A probability distribution is the mathematical function that gives the probabilities of occurrence of a parameter or variable [66]. In the scope of biomechanics, various properties of soft tissues (for example, in different arterial specimens) vary due to different factors such as age, the health status of the donor, and location in the body, among others. For our case, homeostasis in the fiber remodeling process, the different parameters are distributed throughout a specific range that are associated with different values of the internal pressure and axial load (outputs), i.e. the model output is susceptible to the variability of the different input parameters.

The uniform distribution (also known as a rectangular distribution function) of a variable x that we consider is [55]

$$\begin{aligned} f(x) = \left\{ \begin{array}{llllll} \displaystyle \frac{1}{q-p} &{} \quad \text{ for }\quad &{} p< x< q, \\[2ex] 0 &{} \quad \text{ for }\quad &{}x<p\quad \text{ or } \quad x> q. \end{array} \right. \end{aligned}$$
(44)

. where p and q are constants. The uniform distribution will be shown in the form \(x {\sim }\mathcal {U}(p,q)\).

3.3 Statistical measurements for assessment of Sobol method

The assessment of the sensitivity indices obtained using statistical measures represents a perspective of the quality of the results and their robustness. We assess the Sobol indices using bias and standard deviation measures. The bias is gained as [55]

$$\begin{aligned} \textrm{bias}(T)=\mathbb {E}[T] - \theta , \end{aligned}$$
(45)

where \(\theta \) is a variable in a model, T is estimation of \(\theta \), and \(\mathbb {E}[T]\) is the summation of all possible features from a random variable x (the mathematical expectation of T) and is given by

$$\begin{aligned} \mathbb {E}[T]=\int _{-\infty }^{\infty } x g(x)\,\textrm{d}x. \end{aligned}$$
(46)

Standard deviation is another measure that is given by [55]

$$\begin{aligned} SD = \sqrt{\frac{1}{n-1} \sum _{i=1}^n (x_i - \overline{x})^2}, \end{aligned}$$
(47)

where n is a sample size of data, x is a random variable in the model and \(\bar{x}\) is the mean of x.

4 Application of the Sobol method to the problem at hand and assessment of the results

The Sobol method captures the uncertainties of the model output due to variations of individual input parameters values or higher-order interactions mong different input parameters values. To obtain the sensitivity of each parameter in the model, we obtain two main indices: first-order index (see (39)) and total index (see (40)). The first-order index shows output variance due to input variance. Moreover, higher-order terms show interaction among two or more input parameters. Total indices give first-order and higher-order interactions, which correspond to all direct and indirect values from all the parameters. The “Saltelli-Jansen” estimators, as it was explained in Sect. 3, using the uniform distribution for the input parameters, provide the values of the indices. The process to apply the Sobol method is divided into five steps for the analysis of both (33) and (34):

  • The involved input parameters (in either Eq. (33) or (34)) of the model and its sampling ranges under the uniform distribution are specified.

  • Input parameters are assigned with attention to model output using statistical simulation in the program “R”. The sample size is \(N=50,000\) for each input parameter.

  • Sensitivity indices by Saltelli-Janson estimators (Eq. (41) for first-order indices and Eq. (42) for total indices) of input parameters are obtained.

  • Input parameters are sorted based on the highest value of the total indices under the uniform probability distribution.

  • Values of Sobol indices are assessed by means of the bias and standard deviation measures -see Sect. 3.3.

In addition to the assessment given by the last point, the “R" program estimates a first-order index and a total one using a so-called dummy parameter, which is supposed not to influence the output of the model. These (dummy) estimations are interpreted as approximation errors. It follows that if an index value for a given input parameter is smaller (or equal) than the value of the approximation error, then that input parameter is not influential for the output of the model. Furthermore, for each Sobol index, the confidence interval is computed and illustrated accordingly as the lower and upper values of the so called "confidence interval", which is based mainly on 95 % of the value of the index. A 95 % confidence interval means that if we were to take 100 different samples and compute a 95 % confidence interval for each sample, then approximately 95 of the 100 confidence intervals contain the true mean value. In particular, the confidence interval is given as

$$\begin{aligned} CI=\overline{X}\pm Z\frac{s}{\sqrt{n}}, \end{aligned}$$
(48)

where \(\overline{X}\) is the sample mean, Z is the confidence level value, s is the sample standard deviation and n is the sample size. We use a confidence interval level of 95 % since it is taken by convention for different problems.

In what follows, we determine the most sensitive parameters for both the internal pressure \(P_h\) (33) and the axial force \(N_h\) (34). The fiber remodeling process is taken to be in homeostasis. We consider these input parameters: \(\lambda _{i,h}\), the azimuthal stretch at the inner surface of the tube, \(\lambda _z\), the axial stretch, \(\gamma _1\), the initial stiffness in collagen fibers, \(\gamma _2\), the stiffening at larger stretches in the strain stiffening of the fibers, \(\alpha \), the fiber winding angle, \(\mu \), the ground substance parameter, \(k_2\), the sensitivity of the dissolution rate to the fiber stretch, \(R_i\), the inner radius and \(R_e\), the outer radius of the cylinder. Here we recall that the azimuthal stretch at the outer cylindrical surface is linked to the azimuthal stretch at the inner cylindrical surface and the cylindrical geometry via (8). In addition, there are two fixed parameters: the constant fiber creation rate \(\chi _c\) and the fiber dissolution rate \(k_1\) for an unstretched fiber.

4.1 Sensitivity analysis for internal-pressure relation and its assessment

The uniform distributions of the different input parameters are listed in Table 1. The ranges are based on numerical results given in Topol et al. [52]. Furthermore, the fiber creation rate is taken to be \(\chi _c = 0.0010861/ \text{ sec }\), and the fiber dissolution rate for the unstretched fibers is \(k_1 = 0.0010861/\text{sec }\). These values have been obtained by Topol et al. [33], and they are based on the results obtained by Hadi et al. [15] on the strain-dependent enzymatic degradation of collagen fibers and their constant growth.

Table 1 The table gives the ranges of the input parameters (under uniform distribution) taken to study the internal pressure for homeostasis in the fiber remodeling process (see (33))
Full size table
Table 2 Values of the first-order index (\(S_i\)) and total Sobol index (\(T_i\)) for the input parameters associated with \(P_{h}\) (33). All input parameters follow the uniform distribution (\(\mathcal {U}\)(p, q))
Full size table
Fig. 2
figure 2

Sobol indices values for each input parameter as given in Table 1 now as a Bar Plot. The first-order index for the dummy parameter is indicated with a dashed horizontal red line while the total index associated with the dummy parameter is indicated with a dashed horizontal blue line. It follows that some of the total indices are below the \(T_i\) index of the dummy parameter. Moreover, some of the first-order indices of the input parameters are below the \(S_i\) index of the dummy parameter (given by the dashed horizontal red line). The value of the dashed red line is close to zero

Full size image

The values of Sobol indices under uniform distribution are shown in Table 2. Based on the total Sobol indices (\(T_i\)), it follows that \(\lambda _{i,h}\) is the most influential factor on internal pressure. The same result is obtained for first-order Sobol indices. On the other hand, \(\mu \) is the least influential factor on internal pressure based on the total Sobol indices (\(T_i\)).

Furthermore, the Sobol indices (both the first-order index (\(S_i\)) and the total Sobol index (\(T_i\))) are shown as a Bar Plot in Fig. 2. The first-order index for the dummy parameter is indicated with a dashed horizontal red line while the total index associated with the dummy parameter is indicated with a dashed horizontal blue line. For each Sobol index, the confidence interval is computed and illustrated (for each index the interval is given by the two horizontal lines at the top of each rectangle). The result of sorting the sensitive parameters based on \(T_i\) values under uniform distribution (\(\mathcal {U}\)(p, q)) is:

$$\begin{aligned} \begin{array}{llll} {T_i}(\lambda _{i,h})>{T_i}(R_e)>{T_i}(R_i)> {T_i}(\gamma _2)>{T_i}(\lambda _z)\\[3ex] \qquad \qquad> {T_i}(\gamma _1)> {T_i}(k_2)> {T_i}(\alpha )> {T_i}(\mu ). \end{array} \end{aligned}$$
(49)

In addition, Fig. 3 shows pairwise interaction effects between the three most sensitive input parameters, namely, \(\lambda _{i,h}\), \(\gamma _2\) and \(R_i\), on the internal pressure in a multi-scatter plot. The model output (the internal pressure) is indicated with the letter y. The Figure shows three plots. Each of these plots gives for the corresponding two input parameters the sensitivity of the model associated with the joint effect between those two input parameters. Green dots show a significant interaction between the two input parameters on the internal pressure. There are clearly significant green dots between \(\lambda _{i,h}\) and the other two input parameters on the internal pressure.

Fig. 3
figure 3

Interaction impact of Sobol indices between the three most influential parameters in the pressure-inflation relation (33). The variable y is the model’s output, which is the internal pressure \(P_h\)

Full size image
Table 3 Bias and standard deviation measures for Sobol indices associated with internal pressure \(P_{h}\) (33)
Full size table

With regard to the assessment of Sobol indices, we use two statistical measures: bias and standard deviation of indices. The lower the bias and standard deviation values of total indices, the more robust the values of the results obtained. In Table 3, bias measures and standard deviations of Sobol indices under uniform distribution are shown. The bias measures values for all Sobol indices of input parameters are very small. In particular, the bias measures for total Sobol indices of all input parameters are less than 0.001. It follows that Sobol indices for the internal pressure model are reliable. The same conclusion is obtained utilizing the standard deviation given in panel (b) of Table 3.

4.2 Sensitivity analysis for normal force relation and its assessment

Now, in a parallel way to the previous Section, the first-order and total Sobol indices of the different parameters for \(N_h\) given in Eq. (34) are obtained. Results are given in Table 4.

Table 4 The first-order index (\(S_i\)) and total Sobol index (\(T_i\)) of the input parameters for axial force \(N_{h}\) given in Eq. (34)
Full size table

Based on both total Sobol indices (\(T_i\)) and first-order Sobol indices (\(S_i\)), \(\lambda _{i,h}\) is the most influential factor on the axial force. On the other hand, \(\mu \) is the least influential factor on internal pressure under uniform distribution based on the total Sobol indices (\(T_i\)). In addition, the Sobol indices are shown also in Fig. 4. The result of sorting sensitive parameters based on \(T_i\) under uniform distribution (\(\mathcal {U}(p, q)\)) is

$$\begin{aligned} \begin{array}{lllll} {T_i}(\lambda _{i,h})>{T_i}(R_i)>{T_i}(R_e)> {T_i}(\gamma _2)> {T_i}(\lambda _z)\\[3ex]>{T_i}(k_2)> {T_i}(\gamma _1)> {T_i}(\alpha )> {T_i}(\mu ). \end{array} \end{aligned}$$
(50)
Fig. 4
figure 4

Sobol indices for each input parameter associated with the axial force -\(N_h\)- shown in (34) obtained through “Saltelli-Jansen” estimators under uniform distribution as given also in Table 1. With regard to the dashed horizontal blue line it is clear that some of the total indices are below that value. Moreover, with regard to the dashed-horizontal red line it is also clear that some of the first-order indices are below that line. The dashed red line is almost zero

Full size image
Fig. 5
figure 5

Interaction impact of Sobol indices for the 3 most influential parameters associated with the axial force (34) \(N_h\), denoted with the letter y

Full size image

Figure 5 illustrates in a multi-scatter plot the joint interaction effects between the three most sensitive input parameters, namely \(\lambda _{i,h}\), \(\gamma _2\) and \(R_i\), associated with the axial force denoted by y (the output variable). As it was noticed for the internal pressure, there are significant green dots between \(\lambda _{i,h}\) and the two other input parameters.

Table 5 gives bias measures and standard deviations of Sobol indices under uniform distribution. The bias measures values are very small values for both \(S_i\) and \(T_i\) indices. In particular, the bias measures of all input parameters for total Sobol indices are less than 0.05. It follows that the values of Sobol indices are reliable. The same conclusion is obtained examining the standard deviation values given in table 5.

Table 5 Bias and standard deviation measures for Sobol indices associated with normal force (\(N_{h}\)) in the inflated cylinder shown in (34)
Full size table

5 Conclusions and future work

This work applies sensitivity analysis to the inflation and extension of a thick-walled cylinder that consists of an isotropic substance reinforced with two mechanically equivalent and symmetrically disposed families of fibers that undergo a continuous strain-mediated remodeling process. Due to both the symmetrical arrangement of the fibers and that both families of fibers are mechanically equivalent the inflation of the cylinder occurs without a twist.

The main goal of this work is to determine the most influential input parameters on the model outputs, namely the inflation pressure \(P_h\) and the axial force \(N_h\) for a fiber remodeling process in homeostasis. These most influential parameters are identified by applying a (statistical) sensitivity analysis method. Based on the results, the azimuthal stretch \(\lambda {i,h}\) at the inner surface of the tube is the most sensitive parameter for both the inflation pressure \(P_h\) and the axial force \(N_h\). The inner and outer radii \(R_i\) and \(R_e\) of the cylinder follow as the most sensitive parameters among input parameters on the model output. The reliability of the results for the Sobol indices has been confirmed by means of statistical assessment measures -bias measure and standard deviation. This is an emerging theoretical technique in need of experimental data that has important implications for biological material. It is fundamental to analyze the variables with regard to the manner in which the body stores its energy since these aspects give the response (deformation) of the body. It is clear that this theoretical framework (the sensitivity analysis) is other analytical tool to determine and identify which variables need to be retained and how in the development of models.

The results may be useful to understand the influence of material and remodeling parameters and their changes on both the pressure and axial load of arterial soft tissues. For instance, it has been recently recognized (see [39, 67]) that to analyze localized bulging (related to aneurysms) it is important to analyze both the pressure graph and the axial load one with respect to different deformation stretches. It is clear that both the axial load and the pressure are intimately related to the physiological conditions of arteries and, therefore, a rigorous sensitivity analysis of the arterial system needs to consider both of them simultaneously, as it has been done in this paper. Applications of the results may be found in broader research on arterial soft tissue, to determine the consequences of a certain distribution of material parameters (see Sect. 3.2). The results may also be applied to draw some deeper consequences from diagnoses of living tissue to determine the effect of, for example, tissue development processes on the overall structural integrity of the arterial soft tissue. Such remodeling processes were not considered in our previous works [31, 32, 68].

The present work restricts its consideration to the stable inflation of the cylinder. Depending on the type and magnitude of loading, the geometry, and the arrangement and interplay of the different material constituents, inflated cylinders may face various types of instabilities, including bulging, necking, beading, bending, prismatic bifurcation, and helical buckling [35, 69,70,71,72]. The subsequent post-bifurcation processes have been explored, for example, in Topol et al. [39, 73]. It has been shown that the relevance of the different instability modes may vary with changes in the loading, and material volume changes, for example in the form of swelling [42, 43], and the initiation of damage at larger strains [51]. It is clear that before introducing these features is necessary to establish the role of all the parameters under the conditions at hand. Future works also may include further aspects dealing with the sensitivity analysis that include the disruption of homeostasis, for instance, by a change in the inflation pressure, and the approach of a new homeostatic remodeling process that is then associated with a new pressure [22, 24, 28, 33, 52]. The modeling of the dissolution rate function (28) is based on the assumption that the fiber remodeling process is strain stabilized, which is true for a relatively small amount of the fiber stretch. If the collagen fiber stretch becomes sufficiently large, then the enzymatic fiber dissolution process increases as the fiber stretch becomes larger [74,75,76].