Dynamic response of a piezoelectric quasicrystal rod with the generalized thermoelasticity

Abstract

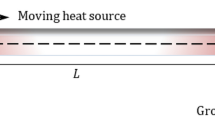
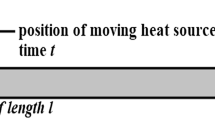
Based on the generalized thermoelastic theory, the physical changes of a finite length rod, which is composed of one-dimensional (1D) hexagonal piezoelectric quasicrystals (PQCs) fixed on both sides and subjected to a moving heat source, are studied. The numerical solutions are obtained using the Laplace transform and its numerical inversion. The effects of displacement, stress, temperature and electric potential on velocity of moving heat source and time were studied. It can be seen from the distribution that the temperature, displacement, electric potential and stress of the rod all increase when the time increases, while the influence of the heat source velocity is opposite.

Appendix A

The constants appearing in Eqs. (29)–(32) are

$$\begin{aligned} \begin{array}{l} g_{1}=\frac{R_{2}c_{1}}{C_{33}c_{2}},g_{2}=\frac{e_{33}^{2}L}{C_{33} \lambda _{33}},g_{3}=\frac{\gamma _{33}T_{0}}{C_{33}},g_{4}=\frac{\rho c_{1} ^{2}}{C_{33}},\\ h_{1}=\frac{R_{2}}{K_{1}},h_{2}=\frac{c_{1}}{c_{2}},h_{3}=\frac{e_{33}d_{33} L}{K_{1}\lambda _{33}},h_{4}=\frac{\rho c_{1}^{3}}{K_{1}c_{2}},\\ k_{1}=\frac{d_{33}c_{1}}{e_{33}c_{2}},k_{2}=\frac{p_{3}T_{0}}{e_{33}},\eta _{1}=\frac{\gamma _{33}}{\rho C_{E}},\eta _{2}=\frac{p_{3}e_{33}L}{\lambda _{33}\rho C_{E}}. \end{array} \end{aligned}$$

(A1)

The constants appearing in Eq. (40) are

$$\begin{aligned} \begin{array}{l} a=h_{3}\left( g_{1}k_{2}+g_{3}k_{1}\right) -h_{2}\left( g_{2}k_{2} -g_{3}L\right) ,b=h_{4}\left( g_{2}k_{2}-g_{3}L\right) ,\\ c=-h_{3}\left( g_{3}+k_{2}\right) +h_{1}\left( g_{2}k_{2}-g_{3}L\right) ,d=h_{3}k_{2}g_{4},\\ l_{1}=k_{2}+g_{3}+c\left( g_{1}k_{2}+g_{3}k_{1}\right) /a,l_{2}=g_{2} k_{2}-g_{3}L,\\ l_{3}=\left( \frac{\left( ad-bc\right) \left( g_{1}k_{2}+g_{3} k_{1}\right) }{a^{2}}-k_{2}g_{4}\right) s^{2},m_{1}=\frac{\left( cg_{1}+a\right) k_{2}}{asg_{3}\left( 1+\tau _{0}s\right) },\\ m_{2}=\frac{a+ck_{1}}{a}-\frac{sk_{2}\left[ a^{2}g_{4}-\left( ad-bc\right) g_{1}\right] }{a^{2}g_{3}\left( 1+\tau _{0}s\right) }-k_{2}\eta _{1},m_{3}=\frac{\left( ad-bc\right) k_{1}s^{2}}{a^{2}},\\ n_{1}=\frac{k_{2}g_{2}}{sg_{3}\left( 1+\tau _{0}s\right) },n_{2}=k_{2} \eta _{2}-L. \end{array} \end{aligned}$$

(A2)

The constants appearing in Eq. (45) are

$$\begin{aligned} \begin{array}{l} a_{1}=a_{2}=\frac{c}{a}+\frac{\left( ad-bc\right) s^{2}}{a^{2}\gamma _{1} ^{2}},a_{3}=a_{4}=\frac{c}{a}+\frac{\left( ad-bc\right) s^{2}}{a^{2} \gamma _{3}^{2}},a_{5}=\frac{c}{a}+\frac{\left( ad-bc\right) v^{2}}{a^{2}},\\ b_{1}=b_{2}=-\frac{\left( l_{1}+l_{3}/\gamma _{1}^{2}\right) }{l_{2}},b_{3}=b_{4}=-\frac{\left( l_{1}+l_{3}/\gamma _{3}^{2}\right) }{l_{2}},b_{5}=-\frac{l_{1}+l_{3}v^{2}/s^{2}}{l_{2}};\\ d_{1}=-d_{2}=-\frac{\gamma _{1}\left( 1+k_{1}a_{1}-Lb_{1}\right) }{k_{2} },d_{3}=-d_{4}=-\frac{\gamma _{3}\left( 1+k_{1}a_{3}-Lb_{3}\right) }{k_{2} },d_{5}=\frac{s\left( 1+k_{1}a_{5}-Lb_{5}\right) }{vk_{2}}. \end{array} \end{aligned}$$

(A3)

The Matrices appearing in Eq. (40) are

$$\begin{aligned} \textbf{M}&=\left[ \begin{array}{cccccccc} 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0\\ \exp \left( \gamma _{1}L\right) &{} \exp \left( \gamma _{2}L\right) &{} \exp \left( \gamma _{3}L\right) &{} \exp \left( \gamma _{4}L\right) &{} 0 &{} 0 &{} 0 &{} 0\\ a_{1} &{} a_{2} &{} a_{3} &{} a_{4} &{} 0 &{} 1 &{} 0 &{} 0\\ a_{1}\exp \left( \gamma _{1}L\right) &{} a_{2}\exp \left( \gamma _{2}L\right) &{} a_{3}\exp \left( \gamma _{3}L\right) &{} a_{4}\exp \left( \gamma _{4}L\right) &{} L &{} 1 &{} 0 &{} 0\\ b_{1} &{} b_{2} &{} b_{3} &{} b_{4} &{} 0 &{} 0 &{} 0 &{} 1\\ b_{1}\exp \left( \gamma _{1}L\right) &{} b_{2}\exp \left( \gamma _{2}L\right) &{} b_{3}\exp \left( \gamma _{3}L\right) &{} b_{4}\exp \left( \gamma _{4}L\right) &{} 0 &{} 0 &{} L &{} 1\\ \Delta _{1} &{} \Delta _{2} &{} \Delta _{3} &{} \Delta _{4} &{} 0 &{} 0 &{} 0 &{} 0\\ \Lambda _{1}\exp \left( \gamma _{1}L\right) &{} \Lambda _{2}\exp \left( \gamma _{2}L\right) &{} \Lambda _{3}\exp \left( \gamma _{3}L\right) &{} \Lambda _{4} \exp \left( \gamma _{4}L\right) &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right] ,\nonumber \\ \textbf{U}&=\left[ \begin{array}{cccccccc} \alpha _{1}&\alpha _{2}&\alpha _{3}&\alpha _{4}&\mu _{1}&\mu _{2}&\mu _{3}&\mu _{4} \end{array} \right] ^{T},\nonumber \\ \textbf{V}&=\left\{ \begin{array}{c} \frac{u_{0}c_{1}\eta _{0}}{s}-\chi \\ \frac{u_{L}c_{1}\eta _{0}}{s}-\chi \exp \left( -\frac{sL}{v}\right) \\ \frac{w_{0}c_{2}\eta _{0}}{s}-a_{5}\chi \\ \frac{w_{L}c_{2}\eta _{0}}{s}-a_{5}\chi \exp \left( -\frac{sL}{v}\right) \\ \frac{c_{1}\eta _{0}\lambda _{33}\phi _{0}}{se_{33}L}-b_{5}\chi \\ \frac{c_{1}\eta _{0}\lambda _{33}\phi _{L}}{se_{33}L}-b_{5}\chi \exp \left( -\frac{sL}{v}\right) \\ \frac{\Theta _{0}}{sT_{0}}+\Delta _{5}\\ \frac{\Theta _{L}}{sT_{0}}+\Lambda _{5}\exp \left( -\frac{sL}{v}\right) \end{array} \right\} , \end{aligned}$$

(A4)

where $\Delta _{i}=d_{i}\left( \delta _{10}+\delta _{20}\gamma _{i}\right) ,\Lambda _{i}=d_{i}\left( \delta _{1\,L}+\delta _{2\,L}\gamma _{i}\right) (i=1,2,3,4),\Delta _{5}=d_{5}\chi \left( \delta _{20}\frac{s}{v}-\delta _{10}\right) ,\Lambda _{5}=d_{5}\chi \left( \delta _{2\,L}\frac{s}{v}-\delta _{1\,L}\right) .$