Vibration and dynamic instability analyses of functionally graded porous doubly curved panels with piezoelectric layers in supersonic airflow

Abstract

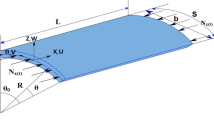
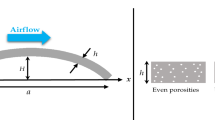
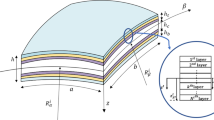
The present study, for the first time, investigates the vibration and flutter analyses of a doubly curved panel composed of functionally graded porous material contained by piezoelectric layers in supersonic flow. In this regard, the first-order piston theory for aerodynamic loading and Reddy’s third-order shear deformation theory for doubly curved panel analysis is used. The governing equations of motion are obtained using Hamilton’s principle and Maxwell’s equation. The Galerkin method is used to discretize the equations of motion. Three types of piezoelectric layers are used, in both open-circuit and closed-circuit electrical boundary conditions. The FG porous material with three types of porosity structure is investigated, including uniform distribution, X-shaped distribution, and V-shaped distribution. Also, the effect of the power of the FG porous material and the porosity coefficient on the frequencies and the flutter boundaries of spherical, cylindrical, doubly curved shell with $R_{y} = - R_{x}$ and plate structures are investigated. The comparison of the spherical panel, doubly curved panel, cylindrical panel, and plate shows that the spherical panel has the highest and the plate has the lowest stability regions. Also, as the radius to length of the panel increases, the critical flutter aerodynamic pressure increases and the flutter frequency decreases. Furthermore, the effects of piezoelectricity, electrical and mechanical boundary conditions, geometric parameters, and the radii of curvatures on the flutter boundaries and flutter frequencies of FG porous doubly curved panels are investigated in detail.

Appendices

Appendix A

In Eq. (20), the terms expressing inertia and the resulting forces and moments are expressed as follows:

$$\left( {I_{0} ,I_{1} ,I_{2} ,I_{3} ,I_{4} ,I_{6} } \right) = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \rho \left( z \right)\left( {1,z,z^{2} ,z^{3} ,z^{4} ,z^{6} } \right) dz$$

(A.1)

$$\begin{aligned} \left( {N_{xx} , N_{xy} ,N_{yy} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xx} , \sigma_{xy} ,\sigma_{yy} } \right) dz \\ \left( {M_{xx} , M_{xy} ,M_{yy} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xx} , \sigma_{xy} ,\sigma_{yy} } \right) zdz \\ \left( {Q_{x} ,Q_{y} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xz} , \sigma_{yz} } \right) dz \\ \left( {S_{xx} , S_{xy} ,S_{yy} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xx} , \sigma_{xy} ,\sigma_{yy} } \right) z^{3} dz \\ \left( {P_{x} ,P_{y} } \right) & = \mathop \int \limits_{{ - h - h_{p} }}^{{h + h_{p} }} \left( {\sigma_{xz} , \sigma_{yz} } \right)z^{2} dz \\ \end{aligned}$$

(A.2)

The stiffness coefficients are presented in Eq. (21) as follows:

$$\begin{aligned} \left( {A_{11} ,A_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} )dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right) dz \\ A_{66} & = \mathop \int \limits_{ - h}^{ - h} Q_{66}^{{}} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right) dz \\ \left( {B_{11} ,B_{12} ,B_{66} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} , Q_{66}^{{}} ) z dz \\ \left( {C_{11} ,C_{12} ,C_{66} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} , Q_{66}^{{}} ) cz^{3} dz \\ \left( {D_{11} ,D_{12} ,D_{66} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} , Q_{66}^{{}} ) z^{2} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} ,\left( {\overline{c}_{11} - \overline{c}_{12} } \right)} \right) z^{2} dz \\ \left( {E_{11} ,E_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} ) \left( {z^{2} - cz^{4} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right)\left( {z^{2} - cz^{4} } \right) dz \\ E_{66} & = \mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right) \left( {z^{2} - cz^{4} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right)\left( {z^{2} - cz^{4} } \right) dz \\ \left( {F_{11} ,F_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} ) cz^{4} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right) cz^{4} dz + \eta_{3} \\ F_{66} & = 2\mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right) cz^{4} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right) cz^{4} dz \\ A_{55} & = \mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right)\left( {1 - \beta z^{2} } \right) dz + + 2\mathop \int \limits_{h}^{{h + h_{p} }} \overline{c}_{55} \left( {1 - \beta z^{2} } \right) dz \\ \left( {G_{11}, G_{12}, G_{66} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} , Q_{66}^{{}} ) z^{3} dz \\ \left( {H_{11}, H_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} ) \left( {z^{4} - cz^{6} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right)\left( {z^{4} - cz^{6} } \right) dz \\ H_{66} & = \mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right)\left( {z^{4} - cz^{6} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right)\left( {z^{4} - cz^{6} } \right) dz \\ \left( {L_{11} ,L_{12} } \right) & = \mathop \int \limits_{ - h}^{ - h} (Q_{11}^{{}} ,Q_{12}^{{}} ) cz^{6} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} ,\overline{c}_{12} } \right) cz^{6} dz \\ L_{66} & = 2\mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{{}} } \right)cz^{6} dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \left( {\overline{c}_{11} - \overline{c}_{12} } \right)cz^{6} dz \\ S_{55} & = \mathop \int \limits_{ - h}^{ - h} \left( {Q_{66}^{b} } \right)\left( {z^{2} - \beta z^{4} } \right) dz + 2\mathop \int \limits_{h}^{{h + h_{p} }} \overline{c}_{55} \left( {z^{2} - \beta z^{4} } \right) dz \\ \end{aligned}$$

(A.3)

The constant quantities in Eq. (22), can be expressed as follow:

$$\begin{aligned} ab_{1} & = A_{{11}} + 2c\frac{{F_{{11}} }}{{R_{x} }} + c^{2} \frac{{H_{{11}} }}{{R_{x}^{2} }} + T_{2} - \frac{{T_{8} }}{{R_{x}^{2} }} + \beta \frac{{T_{{8z2}} }}{{R_{x}^{2} }} - c\frac{{T_{{4z3}} }}{{R_{x}^{2} }} \\ ab_{2} & = A_{{66}} + 2c\frac{{F_{{66}} }}{{R_{x} }} + c^{2} \frac{{H_{{66}} }}{{R_{x}^{2} }} \\ ab_{3} & = \frac{1}{{R_{x}^{2} }}\left( {\beta D_{{55}} - A_{{55}} } \right) \\ ab_{4} & = A_{{12}} + A_{{66}} + \frac{c}{{R_{y} }}\left( {F_{{12}} + F_{{66}} } \right) \\ &\quad + \frac{c}{{R_{x} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{12}} + H_{{66}} } \right) + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ab_{5} & = B_{{11}} - cF_{{11}} + c\frac{{G_{{11}} }}{{R_{x} }} - c^{2} \frac{{H_{{11}} }}{{R_{x} }} + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ab_{6} & = B_{{66}} - c\left( {F_{{66}} - \frac{{G_{{66}} }}{{R_{x} }}} \right) - c^{2} \frac{{H_{{66}} }}{{R_{x} }} \\ ab_{7} & = \frac{1}{{R_{x} }}\left( {A_{{55}} - \beta D_{{55}} } \right) \\ ab_{8} & = B_{{12}} + B_{{66}} - c\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {G_{{12}} + G_{{66}} } \right)\\ &\quad - \frac{{c^{2} }}{{R_{x} }}\left( {H_{{12}} + H_{{66}} } \right) + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ab_{9} & = - c\left( {F_{{11}} + \frac{c}{{R_{x} }}H_{{11}} } \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ab_{{10}} & = - c\left( {F_{{12}} + 2F_{{66}} + \frac{c}{{R_{x} }}\left( {H_{{12}} + 2H_{{66}} } \right)} \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ab_{{11}} & = \frac{1}{{R_{x} }}\left( {A_{{11}} + A_{{55}} - \beta D_{{55}} + \frac{{cF_{{11}} }}{{R_{x} }} + \frac{{A_{{12}} R_{x} }}{{R_{y} }} + \frac{{cF_{{12}} }}{{R_{y} }}} \right) + T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ac_{1} & = A_{{21}} + A_{{66}} + \frac{c}{{R_{x} }}\left( {F_{{21}} + F_{{66}} } \right) + \frac{c}{{R_{y} }}\left( {F_{{21}} + F_{{66}} } \right) \\ &\quad + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{21}} + H_{{66}} } \right) + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ac_{2} & = A_{{66}} + 2c\frac{{F_{{66}} }}{{R_{y} }} + c^{2} \frac{{H_{{66}} }}{{R_{y}^{2} }} \\ ac_{3} & = A_{{22}} + 2c\frac{{F_{{22}} }}{{R_{y} }} + c^{2} \frac{{H_{{22}} }}{{R_{y}^{2} }} + T_{2} + \frac{1}{{R_{y}^{2} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ac_{4} & = \frac{1}{{R_{y}^{2} }}\left( {\beta D_{{44}} - A_{{44}} } \right) \\ ac_{5} & = B_{{21}} + B_{{66}} - c\left( {F_{{21}} + F_{{66}} } \right) + \frac{c}{{R_{y} }}\left( {G_{{21}} + G_{{66}} } \right) \\ &\quad + \frac{1}{{R_{y} }}\left( {T_{7} + T_{8} } \right) - \frac{{c^{2} }}{{R_{y} }}\left( {H_{{21}} + H_{{66}} } \right) + \frac{1}{{R_{y} }}\left( { - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{4z3}} + T_{{3z3}} } \right)} \right) \\ ac_{6} & = B_{{66}} - cF_{{66}} + c\frac{{G_{{66}} }}{{R_{y} }} - c^{2} \frac{{H_{{66}} }}{{R_{y} }} \\ ac_{7} & = B_{{22}} - cF_{{22}} + c\frac{{G_{{22}} }}{{R_{y} }} - c^{2} \frac{{H_{{22}} }}{{R_{y} }} + \frac{1}{{R_{y} }}\left( {T_{7} + T_{8} } \right) \\ &\quad + \frac{1}{{R_{y} }}\left( { - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{4z3}} + T_{{3z3}} } \right)} \right) \\ ac_{8} & = \frac{1}{{R_{y} }}\left( {A_{{44}} - \beta D_{{44}} } \right) \\ ac_{9} & = - c\left( {2F_{{66}} + F_{{21}} + 2\frac{c}{{R_{y} }}H_{{66}} + \frac{c}{{R_{y} }}H_{{21}} } \right) + \frac{1}{{R_{y} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ac_{{10}} & = - c\left( {F_{{22}} + \frac{c}{{R_{y} }}H_{{22}} } \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ac_{{11}} & = \frac{1}{{R_{y} }}\left( {A_{{21}} \frac{{R_{y} }}{{R_{x} }} + A_{{22}} + A_{{44}} - \beta D_{{44}} + \frac{{cF_{{21}} }}{{R_{x} }} + \frac{{cF_{{22}} }}{{R_{y} }}} \right) + T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ad_{1} & = B_{{11}} + \frac{c}{{R_{x} }}G_{{11}} - cF_{{11}} - \frac{{c^{2} }}{{R_{x} }}H_{{11}} + \frac{1}{{R_{x} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right)A_{{66}} \\& \quad + 2c\frac{{F_{{11}} }}{{R_{x} }} + c^{2} \frac{{H_{{11}} }}{{R_{x}^{2} }} + T_{2} - \frac{{T_{8} }}{{R_{x}^{2} }} + \beta \frac{{T_{{8z2}} }}{{R_{x}^{2} }} - c\frac{{T_{{4z3}} }}{{R_{x}^{2} }} \\ ad_{2} & = A_{{66}} + 2c\frac{{F_{{66}} }}{{R_{x} }} + c^{2} \frac{{H_{{66}} }}{{R_{x}^{2} }} \\ ad_{3} & = \frac{1}{{R_{x}^{2} }}\left( {\beta D_{{55}} - A_{{55}} } \right) \\ ad_{4} & = A_{{12}} + A_{{66}} + \frac{c}{{R_{y} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {F_{{12}} + F_{{66}} } \right) \\ &\quad + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{12}} + H_{{66}} } \right) + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ad_{5} & = B_{{11}} - cF_{{11}} + c\frac{{G_{{11}} }}{{R_{x} }} - c^{2} \frac{{H_{{11}} }}{{R_{x} }} + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ad_{6} & = B_{{66}} - c\left( {F_{{66}} - \frac{{G_{{66}} }}{{R_{x} }}} \right) - c^{2} \frac{{H_{{66}} }}{{R_{x} }} \\ ad_{7} & = \frac{1}{{R_{x} }}\left( {A_{{55}} - \beta D_{{55}} } \right) \\ ad_{8} & = B_{{12}} + B_{{66}} - c\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {G_{{12}} + G_{{66}} } \right) - \frac{{c^{2} }}{{R_{x} }}\left( {H_{{12}} + H_{{66}} } \right) \\ &\quad + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ad_{9} & = - c\left( {F_{{11}} + \frac{c}{{R_{x} }}H_{{11}} } \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ad_{{10}} & = - c\left( {F_{{12}} + 2F_{{66}} + \frac{c}{{R_{x} }}\left( {H_{{12}} + 2H_{{66}} } \right)} \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ ad_{{11}} & = \frac{1}{{R_{x} }}\left( {A_{{11}} + A_{{55}} - \beta D_{{55}} + \frac{{cF_{{11}} }}{{R_{x} }} + \frac{{A_{{12}} R_{x} }}{{R_{y} }} + \frac{{cF_{{12}} }}{{R_{y} }}} \right) + T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ af_{1} & = A_{{21}} + A_{{66}} + \frac{c}{{R_{x} }}\left( {F_{{21}} + F_{{66}} } \right) + \frac{c}{{R_{y} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{12}} + H_{{66}} } \right) \\ &\quad + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right)A_{{66}} + 2c\frac{{F_{{11}} }}{{R_{x} }} + c^{2} \frac{{H_{{11}} }}{{R_{x}^{2} }} + T_{2} - \frac{{T_{8} }}{{R_{x}^{2} }} + \beta \frac{{T_{{8z2}} }}{{R_{x}^{2} }} - c\frac{{T_{{4z3}} }}{{R_{x}^{2} }} \\ af_{2} & = A_{{66}} + 2c\frac{{F_{{66}} }}{{R_{x} }} + c^{2} \frac{{H_{{66}} }}{{R_{x}^{2} }} \\ af_{3} & = \frac{1}{{R_{x}^{2} }}\left( {\beta D_{{55}} - A_{{55}} } \right) \\ af_{4} & = A_{{12}} + A_{{66}} + \frac{c}{{R_{y} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {F_{{12}} + F_{{66}} } \right) + \frac{{c^{2} }}{{R_{x} R_{y} }}\left( {H_{{12}} + H_{{66}} } \right) + T_{2} + \frac{1}{{R_{x} R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ af_{5} & = B_{{11}} - cF_{{11}} + c\frac{{G_{{11}} }}{{R_{x} }} - c^{2} \frac{{H_{{11}} }}{{R_{x} }} + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ af_{6} & = B_{{66}} - c\left( {F_{{66}} - \frac{{G_{{66}} }}{{R_{x} }}} \right) - c^{2} \frac{{H_{{66}} }}{{R_{x} }} \\ af_{7} & = \frac{1}{{R_{x} }}\left( {A_{{55}} - \beta D_{{55}} } \right) \\ af_{8} & = B_{{12}} + B_{{66}} - c\left( {F_{{12}} + F_{{66}} } \right) + \frac{c}{{R_{x} }}\left( {G_{{12}} + G_{{66}} } \right) - \frac{{c^{2} }}{{R_{x} }}\left( {H_{{12}} + H_{{66}} } \right) \\ &\quad + \frac{1}{{R_{x} }}\left( {T_{7} + T_{8} } \right) - \frac{\beta }{{R_{x} }}\left( {T_{{7z2}} + T_{{8z2}} } \right) + \frac{c}{{R_{x} }}\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ af_{9} & = - c\left( {F_{{11}} + \frac{c}{{R_{x} }}H_{{11}} } \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ af_{{10}} & = - c\left( {F_{{12}} + 2F_{{66}} + \frac{c}{{R_{x} }}\left( {H_{{12}} + 2H_{{66}} } \right)} \right) + \frac{1}{{R_{x} }}\left( {T_{8} - \beta T_{{8z2}} + cT_{{4z3}} } \right) \\ af_{{11}} & = \frac{1}{{R_{x} }}\left( {A_{{11}} + A_{{55}} - \beta D_{{55}} + \frac{{cF_{{11}} }}{{R_{x} }} + \frac{{A_{{12}} R_{x} }}{{R_{y} }} + \frac{{cF_{{12}} }}{{R_{y} }}} \right) + T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ag_{1} & = \frac{1}{{R_{x} }}\left( { - A_{{55}} + \beta D_{{55}} - A_{{11}} - \frac{c}{{R_{x} }}F_{{11}} - \frac{{R_{x} }}{{R_{y} }}A_{{21}} - \frac{c}{{R_{y} }}F_{{21}} } \right) - T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ag_{2} & = c\left( {F_{{11}} + \frac{c}{{R_{x} }}H_{{11}} } \right) + \frac{1}{{R_{x} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ag_{3} & = c\left( {2F_{{66}} + 2\frac{c}{{R_{x} }}H_{{66}} + F_{{21}} + \frac{c}{{R_{x} }}H_{{21}} } \right) + \frac{1}{{R_{x} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ag_{4} & = \frac{1}{{R_{y} }}\left( { - A_{{44}} + \beta D_{{44}} - A_{{22}} - \frac{c}{{R_{x} }}F_{{12}} - \frac{{R_{y} }}{{R_{x} }}A_{{12}} - \frac{c}{{R_{y} }}F_{{22}} } \right) - T_{2} \left( {\frac{1}{{R_{x} }} + \frac{1}{{R_{y} }}} \right) \\ ag_{5} & = c\left( {F_{{12}} + \frac{c}{{R_{y} }}H_{{12}} + 2F_{{66}} + 2\frac{c}{{R_{y} }}H_{{66}} } \right) + \frac{1}{{R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ag_{6} & = c\left( {F_{{22}} + \frac{c}{{R_{y} }}H_{{22}} } \right) + \frac{1}{{R_{y} }}\left( { - T_{8} + \beta T_{{8z2}} - cT_{{4z3}} } \right) \\ ag_{7} & = A_{{55}} - \beta D_{{55}} - \frac{{B_{{11}} }}{{R_{x} }} + \frac{c}{{R_{x} }}F_{{11}} - \frac{{B_{{21}} }}{{R_{y} }} + \frac{c}{{R_{y} }}F_{{21}} \\ ag_{8} & = c\left( {G_{{12}} - cH_{{11}} } \right) + T_{7} + T_{8} - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ag_{9} & = c\left( {2G_{{66}} - 2cH_{{66}} + G_{{21}} - cH_{{21}} } \right) + T_{7} + T_{8} - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ag_{{10}} & = A_{{44}} - \beta D_{{44}} - \frac{{B_{{12}} }}{{R_{x} }} + \frac{c}{{R_{x} }}F_{{12}} - \frac{{B_{{22}} }}{{R_{y} }} + \frac{c}{{R_{y} }}F_{{22}} \\ ag_{{11}} & = c\left( {G_{{22}} - cH_{{22}} } \right) + T_{7} + T_{8} - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ag_{{12}} & = c\left( {2G_{{66}} - 2cH_{{66}} + G_{{12}} - cH_{{12}} } \right) + T_{7} + T_{8} - \beta \left( {T_{{8z2}} + T_{{7z2}} } \right) + c\left( {T_{{3z3}} + T_{{4z3}} } \right) \\ ag_{{13}} & = - c^{2} H_{{11}} + T_{8} - \beta T_{{8z2}} + cT_{{4z3}} \\ ag_{{14}} & = - c^{2} H_{{22}} + T_{8} - \beta T_{{8z2}} + cT_{{4z3}} \\ ag_{{15}} & = - c^{2} \left( {4H_{{66}} + H_{{21}} + H_{{12}} } \right) + 2T_{8} - 2\beta T_{{8z2}} + 2cT_{{4z3}} \\ ag_{{16}} & = A_{{55}} - \beta D_{{55}} + 2\frac{c}{{R_{x} }}F_{{11}} + \frac{c}{{R_{y} }}\left( {F_{{21}} + F_{{12}} } \right) \\ ag_{{17}} & = A_{{44}} - \beta D_{{44}} + 2\frac{c}{{R_{y} }}F_{{22}} + \frac{c}{{R_{x} }}\left( {F_{{21}} + F_{{12}} } \right) \\ ag_{{18}} & = - \left( {\frac{{A_{{11}} }}{{R_{x}^{2} }} + \frac{1}{{R_{x} R_{y} }}\left( {A_{{12}} + A_{{21}} } \right) + \frac{{A_{{22}} }}{{R_{y}^{2} }}} \right) - T_{2} \left( {\frac{1}{{R_{x}^{2} }} + \frac{1}{{R_{x} R_{y} }}} \right) - T_{2} \left( {\frac{1}{{R_{y}^{2} }} + \frac{1}{{R_{x} R_{y} }}} \right) \\ \end{aligned}$$

(A.4)

For open-circuit condition:

$$\begin{aligned} T_{1} & = \bar{e}_{{31}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi ^{t} }}{{\partial z}}~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\partial \varphi ^{b} }}{{\partial z}}~dz} \right) \\ T_{2} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}~dz \\ T_{3} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )~dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )~dz \\ T_{4} & = - \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}c(h + h_{p} )^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}c(h + h_{p} )^{3} ~dz \\ T_{5} & = e_{{15}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi ^{t} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \varphi ^{b} ~dz} \right) \\ T_{6} & = \frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)dz} \right) \\ T_{7} & = \frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {h + h_{p} } \right)\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)dz} \right) \\ T_{8} & = c\frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {h + h_{p} } \right)^{3} \left( { - \mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)dz} \right) \\ T_{{1z}} & = \bar{e}_{{31}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi ^{t} }}{{\partial z}}z~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\partial \varphi ^{b} }}{{\partial z}}z~dz} \right) \\ T_{{2z}} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}z~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}z~dz \\ T_{{3z}} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )z~dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )z~dz \\ T_{{4z}} & = - \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}cz(h + h_{p} )^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}cz(h + h_{p} )^{3} ~dz \\ T_{{1z3}} & = \bar{e}_{{31}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi ^{t} }}{{\partial z}}z^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\partial \varphi ^{b} }}{{\partial z}}z^{3} ~dz} \right) \\ T_{{2z3}} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}z^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}z^{3} ~dz \\ T_{{3z3}} & = \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )z^{3} ~dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}(h + h_{p} )z^{3} ~dz \\ T_{{4z3}} & = - \mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}cz^{3} (h + h_{p} )^{3} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \frac{{\bar{e}_{{31}}^{2} }}{{\bar{\Xi }_{{33}} }}cz^{3} (h + h_{p} )^{3} ~dz \\ T_{{5z2}} & = e_{{15}} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} z^{2} \varphi ^{t} ~dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} z^{2} \varphi ^{b} ~dz} \right) \\ T_{{6z2}} & = \frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)z^{2} dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)z^{2} dz} \right) \\ T_{{7z2}} & = \frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {h + h_{p} } \right)\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)z^{2} dz - \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)z^{2} dz} \right) \\ T_{{8z2}} & = c\frac{{e_{{15}} \bar{e}_{{31}} }}{{\bar{\Xi }_{{33}} }}\left( {h + h_{p} } \right)^{3} \left( { - \mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)z^{2} dz + \mathop \int \limits_{{ - h - h_{p} }}^{{ - h}} \left( {z + h} \right)z^{2} dz} \right) \\ \end{aligned}$$

(A.5)

and for closed-circuit condition:

$$\begin{aligned} T_{1} & = \overline{e}_{31} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi^{t} }}{\partial z} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \frac{{\partial \varphi^{b} }}{\partial z} dz} \right), \\ T_{5} & = e_{15} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \varphi^{b} dz} \right), \\ T_{1z} & = \overline{e}_{31} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi^{t} }}{\partial z}z dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \frac{{\partial \varphi^{b} }}{\partial z}z dz} \right), \\ T_{1z3} & = \overline{e}_{31} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{\partial \varphi^{t} }}{\partial z}z^{3} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \frac{{\partial \varphi^{b} }}{\partial z}z^{3} dz} \right), \\ T_{5z2} & = e_{15} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} z^{2} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} z^{2} \varphi^{b} dz} \right) \\ T_{2} & = T_{3} = T_{4} = T_{6} = T_{7} = T_{8} = T_{2z} = T_{3z} = T_{4z} = T_{2z3} = T_{3z3} = T_{4z3} = T_{6z2} = T_{7z2} = T_{8z2} = 0, \\ \end{aligned}$$

(A.6)

Appendix B

In Eq. (26), the definitions of constant quantities are expressed as follows:

For open-circuit condition:

$$\begin{aligned} \varphi^{t} & = 1 - \left( {\frac{{z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} , \varphi^{b} = 1 - \left( {\frac{{ - z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} \\ S_{1} & = \mathop \int \limits_{h}^{{h + h_{p} }} e_{15} \left( {1 - \beta z^{2} } \right) dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} e_{15} \left( {1 - \beta z^{2} } \right) dz \\ S_{2} & = {\Xi }_{11} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \varphi^{b} dz} \right) \\ S_{3} & = \mathop \int \limits_{h}^{{h + h_{p} }} \overline{e}_{31} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \overline{e}_{31} dz \\ S_{4} & = \mathop \int \limits_{h}^{{h + h_{p} }} \overline{e}_{31} \beta z^{2} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \overline{e}_{31} \beta z^{2} dz \\ S_{5} & = {\overline{\Xi }}_{33} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \frac{{d^{2} \varphi^{t} }}{{dz^{2} }} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \frac{{d^{2} \varphi^{b} }}{{dz^{2} }} dz} \right) \\ S_{6} & = S_{7} = S_{8} = 0 \\ \end{aligned}$$

(B.1)

and for closed-circuit condition:

$$\begin{aligned} \varphi^{t} & = 1 + \frac{{4\left( {z - h} \right)}}{{h_{p} }} - \left( {\frac{{z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} \\ \varphi^{b} & = 1 - \frac{{4\left( {z + h} \right)}}{{h_{p} }} - \left( {\frac{{ - z - h - h_{p} /2}}{{h_{p} /2}}} \right)^{2} \\ S_{1} & = \mathop \int \limits_{h}^{{h + h_{p} }} e_{15} \left( {1 - \beta z^{2} } \right) dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} e_{15} \left( {1 - \beta z^{2} } \right) dz \\ S_{2} & = {\Xi }_{11} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \varphi^{b} dz} \right) \\ S_{3} & = \mathop \int \limits_{h}^{{h + h_{p} }} \overline{e}_{31} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \overline{e}_{31} dz \\ S_{4} & = \mathop \int \limits_{h}^{{h + h_{p} }} \overline{e}_{31} \beta z^{2} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \overline{e}_{31} \beta z^{2} dz \\ S_{5} & = {\overline{\Xi }}_{33} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \varphi^{t} dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \varphi^{b} dz} \right) \\ S_{6} & = \frac{{{\Xi }_{11} \overline{e}_{31} }}{{{\overline{\Xi }}_{33} }}\left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \left( {z + h} \right)dz} \right) \\ S_{7} & = \frac{{{\Xi }_{11} \overline{e}_{31} }}{{{\overline{\Xi }}_{33} }}\left( {h + h_{p} } \right)\left( { - \mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz + \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \left( {z + h} \right)dz} \right) \\ S_{8} & = \frac{{{\Xi }_{11} \overline{e}_{31} }}{{{\overline{\Xi }}_{33} }}\left( {h + h_{p} } \right)^{3} \left( {\mathop \int \limits_{h}^{{h + h_{p} }} \left( {z - h} \right)dz - \mathop \int \limits_{{ - h - h_{p} }}^{ - h} \left( {z + h} \right)dz} \right) \\ \end{aligned}$$

(B.2)