On vibration and passive control of axially translating string with damping at both ends using reflected traveling wave superposition method

Abstract

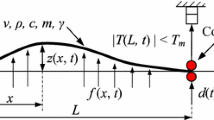
The axially translating string has received wide attention due to its adverse effect of transverse vibration on security and stability in engineering. Most of the current literature focuses on classical boundary cases (e.g., fixed boundary, free boundary), while non-classical boundaries, such as damped boundary, spring-damped boundary, and mass-spring-damped boundary, are more relevant because they are in line with engineering practice. Boundary damping has a significant effect on system vibration, and the damping-damping boundary has rarely been studied. Thus, this paper is dedicated to the modeling, calculation and vibration passive control of a translating string with damping at both ends. First, the equations of motion and boundary conditions are deduced according to extended Hamilton’s principle, with the boundary damping forces as the controlling forces. Second, the analytical solutions of vibration response and system energy expressions are derived using the reflected traveling wave superposition method (RTWSM). Next, to stabilize the system under the boundary damping forces, the boundary damping ranges that satisfy the exponential decay of the system energy are obtained. To further solve for optimal damping in the above ranges, RTWSM model and the boundary energy reflection are employed. Finally, the vibration responses of translating strings with different boundary damping values are simulated. The result shows that boundary damping in feasible intervals facilitates vibration attenuation effectively.

Appendix A. The derivation of governing equation and boundary condition.

In order to simplify the derivation, the notation La shown in Eq. (A.1):

$$La = \rho (U_{,T} + V_{0} U_{,X} )^{2} - T_{0} U_{,X}^{2}$$

(A.1)

Then, according to Eqs. (2) and (3), the following equation is obtained:

$$\begin{aligned} \int_{{T_{1} }}^{{T_{2} }} {\delta (E_{{\text{k}}} - E_{{\text{p}}} )} &= \int_{{T_{1} }}^{{T_{2} }} {\delta \left( {\frac{1}{2}\int_{0}^{L} {\left( {\rho (U_{,T} + V_{0} U_{,X} )^{2} - T_{0} U_{,X}^{2} } \right)} {\text{d}}X} \right){\text{d}}T} \hfill \\ &= \frac{1}{2}\int_{{T_{1} }}^{{T_{2} }} {\int_{0}^{L} {\delta L} a{\text{d}}X{\text{d}}T} = \frac{1}{2}\int_{{T_{1} }}^{{T_{2} }} {\int_{0}^{L} {\left( {\frac{\partial La}{{\partial U}}\delta U + \frac{\partial La}{{\partial U_{,X} }}\delta U_{,X} + \frac{\partial La}{{\partial U_{,T} }}\delta U_{,T} } \right)} {\text{d}}X{\text{d}}T} \hfill \\ \end{aligned}$$

(A.2)

We integrate it by parts, the Eq. (A.2) can be written in the following form:

$$\begin{aligned}& \frac{1}{2}\int_{{T_{1} }}^{{T_{2} }} {\int_{0}^{L} {\left( {\frac{\partial La}{{\partial U}}\delta U + \frac{\partial La}{{\partial U_{,X} }}\delta U_{,X} + \frac{\partial La}{{\partial U_{,T} }}\delta U_{,T} } \right)} {\text{d}}X{\text{d}}T} \\ &\quad= \frac{1}{2}\int_{{T_{1} }}^{{T_{2} }} {\int_{0}^{L} {\left( {\frac{\partial La}{{\partial U}} - \frac{\partial }{\partial X}\frac{\partial La}{{\partial U_{,X} }} - \frac{\partial }{\partial T}\frac{\partial La}{{\partial U_{,T} }}} \right)} \delta U{\text{d}}X{\text{d}}T} + \frac{1}{2}\int_{{T_{1} }}^{{T_{2} }} {\frac{\partial La}{{\partial U_{,X} }}\delta U\left| \begin{aligned} X &= L \hfill \\ X &= 0 \hfill \\ \end{aligned} \right.} {\text{d}}T \\ &\qquad + \frac{1}{2}\int_{0}^{L} {\frac{\partial La}{{\partial U_{,T} }}\delta U\left| \begin{aligned} T &= T_{2} \hfill \\ T &= T_{1} \hfill \\ \end{aligned} \right.} {\text{d}}T \hfill \\ &\quad= \int_{{T_{1} }}^{{T_{2} }} {\int_{0}^{L} {\left( { - \rho [V_{0}^{2} U_{,XX} + 2V_{0} U_{,XT} + U_{,TT} ] + T_{0} U_{,XX} } \right)} \delta U{\text{d}}X{\text{d}}T + \frac{1}{2}\int_{{T_{1} }}^{{T_{2} }} {\frac{\partial La}{{\partial U_{,X} }}\delta U\left| \begin{aligned} X &= L \hfill \\ X &= 0 \hfill \\ \end{aligned} \right.} {\text{d}}T} \hfill \\ &\qquad+ \frac{1}{2}\int_{0}^{L} {\frac{\partial La}{{\partial U_{,T} }}\delta U\left| \begin{aligned} T &= T_{2} \hfill \\ T &= T_{1} \hfill \\ \end{aligned} \right.} {\text{d}}T \hfill \\ \end{aligned}$$

(A.3)

Because the variations at T₁ and T₂ are zero, i.e., δU(X,T₁) = δU(X,T₂) = 0, the last term in Eq. (A.3) vanishes. Then, we substitute Eqs. (4), (5) and (A.3) into Eq. (1),

$$\begin{aligned} & \frac{1}{2}\int_{{T_{1} }}^{{T_{2} }} {\int_{0}^{L} {\left( { - \rho [V_{0}^{2} U_{{,XX}} + 2V_{0} U_{{,XT}} + U_{{,TT}} ] + T_{0} U_{{,XX}} } \right)} \delta U{\text{d}}X{\text{d}}T} \\ & \qquad + \left( {\frac{1}{2}\int_{{T_{1} }}^{{T_{2} }} {\frac{{\partial La}}{{\partial U_{{,X}} }}\delta U\left| \begin{gathered} X = L \hfill \\ X = 0 \hfill \\ \end{gathered} \right.} {\text{ + }}\delta W_{{nc}} + \delta W_{{vm}} } \right){\text{d}}T \\ & \quad = \int_{{T_{1} }}^{{T_{2} }} {\int_{0}^{L} {\left( { - \rho [V_{0}^{2} U_{{,XX}} + 2V_{0} U_{{,XT}} + U_{{,TT}} ] + T_{0} U_{{,XX}} } \right)} \delta U{\text{d}}X{\text{d}}T} \\ & \qquad + \int_{{T_{1} }}^{{T_{2} }} {\left( {\begin{array}{*{20}l} {\left( {\rho V_{0} \left( {U_{{,T}} + V_{0} U_{{,X}} } \right) - T_{0} U_{{,X}} } \right)\delta U\left| \begin{gathered} X = L \hfill \\ X = 0 \hfill \\ \end{gathered} \right. - H_{0} U_{{,X}} (0,T)\delta U(0,T)} \hfill \\ { - H_{1} U_{{,T}} (L,T)\delta U(L,T) + \rho V_{0} [U_{{,T}} (0,T) + VU_{{,X}} (0,T)]\delta U(0,T)} \hfill \\ { - \rho V_{0} [U_{{,T}} (L,T) + V_{0} U_{{,X}} (L,T)]\delta U(L,T)} \hfill \\ \end{array} } \right){\text{d}}T} \\ & \quad = \int_{{T_{1} }}^{{T_{2} }} {\int_{0}^{L} {\left( { - \rho [V_{0}^{2} U_{{,XX}} + 2V_{0} U_{{,XT}} + U_{{,TT}} ] + T_{0} U_{{,XX}} } \right)} \delta U{\text{d}}X{\text{d}}T} \\ & \qquad + \int_{{T_{1} }}^{{T_{2} }} {\{ - (T_{0} U_{{,X}} (L,T) + H_{1} U_{{,T}} (L,T))\delta U(L,T) + (T_{0} U_{{,X}} (0,T) - H_{0} U_{{,T}} (0,T))\delta U(0,T)\} {\text{d}}T} =0 \end{aligned}$$

(A.4)

Thus, the governing equation and boundary conditions at X = 0 and X = L are obtained as follows:

$$- \rho [V_{0}^{2} U_{,XX} + 2V_{0} U_{,XT} + U_{,TT} ] + T_{0} U_{,XX} = 0$$

(A.5)

$$T_{0} U_{,X} (0,T) - H_{0} U_{,T} (0,T) = 0$$

(A.6)

$$T_{0} U_{,X} (L,T) + H_{1} U_{,T} (L,T) = 0$$

(A.7)