Skip to main content
SpringerLink
Log in

Vibration analysis of a multilayer functionally graded cylinder with effects of graded-index and boundary conditions

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

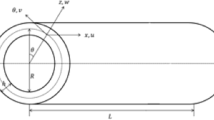
The materials industry is under increasing pressure to enhance performance while lowering costs and environmental impact. Three layers of functionally graded materials (FGMs) were proposed as a solution to this problem. The general goal of this research is to develop a semi-analytical method for solving the free vibration problem of FGMs in an infinite-length composite cylinder made of stainless steel (SS) and silicon nitride (SN). The formulation is based on Legendre polynomial approach and the use of specific rectangle window functions. This approach will result in an eigenvalue/eigenvector issue in the computation of normalized frequencies and displacement profiles. The effective material properties of FGM cylinders vary following the radial direction in conformity with the power-law distribution of the volume fractions. The numerical iteration approach was generated to create data utilizing MATLAB apps to investigate the free vibration analysis from specified boundary conditions. The results are obtained for longitudinal, torsional, and flexural modes. Then, the propagation of guided waves in three-layers (SN/SS/SN) of functionally graded cylinder with diverse gradient for each mode is studied. Accordingly, the results obtained demonstrate that the volumetric fraction of the FGM cylinder is significantly impacted by the graded-index. In addition, the graded-index has a major influence on the variation of the material’s properties in the radial direction. Furthermore, the dispersion curves of the normalized frequencies and phase velocities are significantly influenced by the graded-index. These results demonstrate that the phase velocities of the same mode increase as the exponents of the power-law increase. The displacement distributions are also explored to better understand the characteristics of the guiding waves inside the materials. Furthermore, the boundary conditions have a more significant influence on the normal stresses. High accuracy is found between our results and those published in the literature (error = 0.58%). This paper provides an important insight into the propagation of ultrasonic-guided waves in functionally graded multilayer cylindrical constructs for non-destructive testing.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Liu, Z., Meyers, M.A., Zhang, Z., Ritchie, R.O.: Functional gradients and heterogeneities in biological materials: Design principles. functions, and bioinspired applications. Prog. Mater. Sci. 88, 467–498 (2017). https://doi.org/10.1016/j.pmatsci.2017.04.013

    Article  Google Scholar 

  2. Kumar, S., Reddy, K.M., Kumar, A., Devi, G.R.: Development and characterization of polymer–ceramic continuous fiber reinforced functionally graded composites for aerospace application. Aerospace Sci. Technol. 26(1), 185–191 (2013). https://doi.org/10.1016/j.ast.2012.04.002

    Article  Google Scholar 

  3. Yin, J., Lu, L., Cui, Y., Cao, Y., Zhang, P., Yan, Y., Du, Y.: Functional gradient films on aluminum alloy with high absorption efficiencies and damage thresholds for inertial confinement fusion applications. Ceram. Int. 48(13), 19180–19190 (2022). https://doi.org/10.1016/j.ceramint.2022.03.209

    Article  Google Scholar 

  4. Pompe, W., Worch, H., Epple, M., Friess, W., Gelinsky, M., Greil, P., Schulte, K.J.M.S.: Functionally graded materials for biomedical applications. Mater. Sci. Eng. A 362(1–2), 40–60 (2003). https://doi.org/10.1016/S0921-5093(03)00580-X

    Article  Google Scholar 

  5. Yang, Y., Liu, Y.: A new boundary element method for modeling wave propagation in functionally graded materials. Eur. J. Mech. A Solids. 80, 103897 (2020). https://doi.org/10.1016/j.euromechsol.2019.103897

    Article  MathSciNet  MATH  Google Scholar 

  6. Lefebvre, J.E., Zhang, V., Gazalet, J., Gryba, T., Sadaune, V.: Acoustic wave propagation in continuous functionally graded plates: an extension of the Legendre polynomial approach. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 48(5), 1332–1340 (2001). https://doi.org/10.1109/58.949742

    Article  Google Scholar 

  7. Yu, J.G., Ratolojanahary, F.E., Lefebvre, J.E.: Guided waves in functionally graded viscoelastic plates. Compos. Struct. 93(11), 2671–2677 (2011). https://doi.org/10.1016/j.compstruct.2011.06.009

    Article  Google Scholar 

  8. Yu, J., Lefebvre, J.E., Elmaimouni, L.: Guided waves in multilayered plates: an improved orthogonal polynomial approach. Acta Mech. Solida Sin. 27(5), 542–550 (2014). https://doi.org/10.1016/S0894-9166(14)60062-8

    Article  Google Scholar 

  9. Zhang, B., Yu, J.G., Zhang, X.M., Elmaimouni, L.: Guided wave propagating in a 1-D hexagonal piezoelectric quasi-crystal plate. Acta Mech. 232(1), 135–151 (2021). https://doi.org/10.1007/s00707-020-02811-7

    Article  MathSciNet  MATH  Google Scholar 

  10. Zhang, B., Yu, J., Zhang, X., &Elmaimouni, L.: Guided wave characteristics in the functionally graded two‐dimensional hexagonal quasi‐crystal plate. ZAMM J. App. Math. Mech./Zeitschrift für AngewandteMathematik und Mechanik, 100(11), e201900210 (2020). https://doi.org/10.1002/zamm.201900210

  11. Zhang, B., Yu, J., Zhou, H., Zhang, X., Elmaimouni, L.: Guided waves in a functionally graded 1-D hexagonal quasi-crystal plate with piezoelectric effect. J. Intell. Mater. Syst. Struct. 33(13), 1678–1696 (2022). https://doi.org/10.1177/1045389X211063952

    Article  Google Scholar 

  12. Liu, C., Yu, J., Xu, W., Zhang, X., Wang, X.: Dispersion characteristics of guided waves in functionally graded anisotropic micro/nano-plates based on the modified couple stress theory. Thin-Walled Struct 161, 107527 (2021). https://doi.org/10.1016/j.tws.2021.107527

    Article  Google Scholar 

  13. Amor, M.B., Salah, I.B., Ghozlen, M.H.B.: Propagation behavior of lamb waves in functionally graded piezoelectric plates. Acta Acustica United Acustica 101(3), 435–442 (2015). https://doi.org/10.3813/AAA.918839

    Article  Google Scholar 

  14. Kiełczyński, P., Szalewski, M., Balcerzak, A., Wieja, K.: Inverse method for determining profiles of elastic parameters in the functionally graded materials using love waves. Acta Acust. Acust. 102(3), 428–435 (2016). https://doi.org/10.3813/AAA.918961

    Article  Google Scholar 

  15. Li, C.L., Han, Q., Liu, Y.J., Xiao, D.L.: Guided wave propagation in rotating functionally graded annular plates. Acta Mech. 228(3), 1083–1095 (2017). https://doi.org/10.1007/s00707-016-1752-9

    Article  MathSciNet  MATH  Google Scholar 

  16. Wang, X.X., Yu, J.G., Zhang, B., Elmaimouni, L., Zhang, X.M., Wang, X.H.: Lamb waves propagating in functionally graded 1-D quasi-crystal couple stress nanoplates. Acta Mech. 233(8), 3021–3033 (2022). https://doi.org/10.1007/s00707-022-03274-8

    Article  MathSciNet  MATH  Google Scholar 

  17. Daikh, A.A., Belarbi, M.O., Ahmed, D., et al.: Static analysis of functionally graded plate structures resting on variable elastic foundation under various boundary conditions. Acta Mech (2022). https://doi.org/10.1007/s00707-022-03405-1

    Article  Google Scholar 

  18. Gong, S.W., Lam, K.Y., Reddy, J.N.: The elastic response of functionally graded cylindrical shells to low-velocity impact. Int. J. Impact Eng. 22(4), 397–417 (1999). https://doi.org/10.1016/S0734-743X(98)00058-X

    Article  Google Scholar 

  19. Han, X., Liu, G.R., Xi, Z.C., Lam, K.Y.: Characteristics of waves in a functionally graded cylinder. Int. J. Numer. Meth. Eng. 53(3), 653–676 (2002). https://doi.org/10.1002/nme.305

    Article  MATH  Google Scholar 

  20. Han, X., Liu, G.R.: Elastic waves in a functionally graded piezoelectric cylinder. Smart Mater. Struct. 12(6), 962–971 (2003). https://doi.org/10.1088/0964-1726/12/6/014

    Article  Google Scholar 

  21. Wu, B., Su, Y., Liu, D., Chen, W., Zhang, C.: On propagation of axisymmetric waves in pressurized functionally graded elastomeric hollow cylinders. J. Sound Vib. 421, 17–47 (2018). https://doi.org/10.1016/j.jsv.2018.01.055

    Article  Google Scholar 

  22. Bezzie, Y.M., Woldemichael, D.E.: Effects of graded-index and Poisson’s ratio on elastic-solutions of a pressurized functionally graded material thick-walled cylinder. Forces Mech. 4, 100032 (2021). https://doi.org/10.1016/j.finmec.2021.100032

    Article  Google Scholar 

  23. Chan, D.Q., Quan, T.Q., Phi, B.G., et al.: Buckling analysis and dynamic response of FGM sandwich cylindrical panels in thermal environments using nonlocal strain gradient theory. Acta Mech. 233, 2213–2235 (2022). https://doi.org/10.1007/s00707-022-03212-8

    Article  MathSciNet  MATH  Google Scholar 

  24. Elmaimouni, L., Lefebvre, J.E., Zhang, V., Gryba, T.:Guided waves in radially graded cylinders: a polynomial approach. NDT&E International 38(3), 344–353 (2005). https://doi.org/10.1016/j.ndteint.2004.10.004.

  25. Zhang, B., Yu, J.G., Zhang, X.M., Wang, X.H.: Waves in the multilayered one-dimensional hexagonal quasi-crystal plates. Acta Mech. Solida Sin. 34(1), 91–103 (2021)

    Article  Google Scholar 

  26. Zhang, B., Wang, X.H., Elmaimouni, L., Yu, J.G., Zhang, X.M.: Axial guided wave characteristics in functionally graded one-dimensional hexagonal piezoelectric quasi-crystal cylinders. Math. Mech. Solids 27, 125–143 (2021). https://doi.org/10.1177/10812865211013458

    Article  MathSciNet  MATH  Google Scholar 

  27. Zhang, X., Li, Z., Yu, J., Zhang, B.: Properties of circumferential non-propagating waves in functionally graded piezoelectric cylindrical shells. Adv. Mech. Eng. 11(4), 168781401983687 (2019). https://doi.org/10.1177/1687814019836878

    Article  Google Scholar 

  28. Yu, J.G., Zhang, B., Elmaimouni, L., Zhang, X.M.: Guided waves in layered cylindrical structures with sectorial cross-section under axial initial stress. Mech. Adv. Mater. Struct. 28(5), 457–466 (2021). https://doi.org/10.1080/15376494.2019.1572842

    Article  Google Scholar 

  29. Auld, B.A.: Acoustic fields and waves in solids. Krieger, Malabar, FL (1990)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lab PETI-ERMAM, Polydisciplinary Faculty of Ouarzazate, Ibn Zohr University, BP.638, 45000, Ouarzazate, Morocco

    Rabab Raghib, Ismail Naciri, Hassna Khalfi & Lahoucine Elmaimouni

  2. LM3ER-OTEA, Department of Physics, Faculty of Sciences and Techniques, Moulay Ismail University of Meknes, BP.509, Boutalamine, 52000, Errachidia, Morocco

    Abdellah Benami

  3. School of Mechanical and Power Engineering, Henan Polytechnic University, Jiaozuo, 454003, China

    Jiangong Yu

  4. Laboratory of Physic and Chemistry, Faculty of Science, Ibn Zohr University, Agadir, Morocco

    Lahcen El Maimouni

Authors
  1. Rabab Raghib
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ismail Naciri
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hassna Khalfi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lahoucine Elmaimouni
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Abdellah Benami
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Jiangong Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Lahcen El Maimouni
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rabab Raghib.

Ethics declarations

Conflict of interest

The authors declare no competing of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The elements needed to calculate the eigenvalues and eigenvectors:

$$\begin{aligned}{{}_{j}^{m}A}_{11}^{l}=& \frac{1}{{\left(kH\right)}^{l}}\left\{\left[{C}_{11}^{\left(l\right)}{q}_{1}^{l+2} {u{^{\prime}}{^{\prime}}}_{1}+\left(1+l\right){C}_{11}^{\left(l\right)}{q}_{1}^{l+1} {u{^{\prime}}}_{1}+\left(l{C}_{12}^{\left(l\right)}-{C}_{22}^{\left(l\right)}-{n}^{2} {C}_{66}^{\left(l\right)}\right){q}_{1}^{l}{u}_{1}-{C}_{55}^{\left(l\right)}{q}_{1}^{l+2} {u}_{1}\right]\pi \left(ka, kb\right)\right.\\ &\left.+\left[{C}_{11}^{\left(l\right)}{q}_{1}^{l+2}{u{^{\prime}}}_{1}+{C}_{12}^{\left(l\right)}{q}_{1}^{l+1}{u}_{1}\right] \left(\delta \left({q}_{1}=ka\right)-\delta \left({q}_{1}=kb\right)\right)\right\}\end{aligned}$$
$$\begin{aligned}{{}_{j}^{m}A}_{12}^{l}=&\frac{1}{{\left(kH\right)}^{l}} \left\{\left[-in\left({C}_{12}^{\left(l\right)}+{C}_{66}^{\left(l\right)}\right){q}_{1}^{l+1}{{u}^{^{\prime}}}_{2}+in\left(l{C}_{22}^{\left(l\right)}-{C}_{66}^{\left(l\right)}-{C}_{12}^{\left(l\right)}\right){q}_{1}^{l}{u}_{2}\right] \pi \left(ka, kb\right)\right.\\ &\left.+\left[in{C}_{12}^{\left(l\right)}{q}_{1}^{l+1}{u}_{2}\right]\left(\delta \left({q}_{1}=ka\right)-\delta \left({q}_{1}=kb\right)\right)\right\}\end{aligned}$$
$$\begin{aligned}{{}_{j}^{m}A}_{13}^{l}=& \frac{1}{{\left(kH\right)}^{l}}\left\{\left[-i\left({C}_{13}^{\left(l\right)}+{C}_{55}^{\left(l\right)}\right){q}_{1}^{l+2}{{u}^{^{\prime}}}_{3}-i\left(\left(1+l\right){C}_{13}^{\left(l\right)}-{C}_{23}^{\left(l\right)}\right){q}_{1}^{l+1}{u}_{3}\right] \pi \left(ka, kb\right)\right.\\ &\left.-\left[i{C}_{13}^{\left(l\right)}{q}_{1}^{l+2}{u}_{3}\right]\left(\delta \left({q}_{1}=ka\right)-\delta \left({q}_{1}=kb\right)\right)\right\}\end{aligned}$$
$$\begin{aligned}{{}_{j}^{m}A}_{21}^{l}=& \frac{1}{{\left(kH\right)}^{l}}\left\{\left[in\left({C}_{12}^{\left(l\right)}+{C}_{66}^{\left(l\right)}\right){q}_{1}^{l+1}{{u}^{^{\prime}}}_{1}+in\left({C}_{22}^{\left(l\right)}+\left(1+l\right){C}_{66}^{\left(l\right)}\right){q}_{1}^{l}{u}_{1}\right] \pi \left(ka, kb\right)\right.\\ &\left.+\left[{inC}_{66}^{\left(l\right)}{q}_{1}^{l+1}{u}_{1}\right]\left(\delta \left({q}_{1}=ka\right)-\delta \left({q}_{1}=kb\right)\right)\right\}\end{aligned}$$
$$\begin{aligned}{{}_{j}^{m}A}_{22}^{l}=& \frac{1}{{\left(kH\right)}^{l}}\left\{\left[-\left({n}^{2}{C}_{22}^{\left(l\right)}+\left(1+l\right){C}_{66}^{\left(l\right)}\right){q}_{1}^{l}{u}_{2}+{C}_{66}^{\left(l\right)}{q}_{1}^{l+2}{{u}^{{^{\prime}}{^{\prime}}}}_{2}+\left(1+l\right){C}_{66}^{\left(l\right)}{q}_{1}^{l+1}{{u}^{^{\prime}}}_{2}-{{C}_{44}^{\left(l\right)}q}_{1}^{l+2}{u}_{2}\right] \pi \left(ka, kb\right)\right.\\ &\left.+\left[{C}_{66}^{\left(l\right)}\left({q}_{1}^{l}{u{^{\prime}}}_{2}-{q}_{1}^{l+1}{u}_{2}\right)\right]\left(\delta \left({q}_{1}=ka\right)-\delta \left({q}_{1}=kb\right)\right)\right\}\end{aligned}$$
$${{}_{j}^{m}A}_{23}^{l}= \frac{1}{{\left(kH\right)}^{l}}\left\{\left[n\left({C}_{23}^{\left(l\right)}+{C}_{44}^{\left(l\right)}\right){q}_{1}^{l+1}{u}_{3}\right]\pi \left(ka, kb\right)\right\}$$
$$\begin{aligned}{{}_{j}^{m}A}_{31}^{l}=& \frac{1}{{\left(kH\right)}^{l}}\left\{\left[-i\left({C}_{13}^{\left(l\right)}+{C}_{55}^{\left(l\right)}\right){q}_{1}^{l+2}{{u}^{^{\prime}}}_{1}-i\left({C}_{23}^{\left(l\right)}+\left(1+l\right){C}_{55}^{\left(l\right)}\right){q}_{1}^{l+1}{u}_{1}\right] \pi \left(ka, kb\right)\right.\\ &\left.-\left[{iC}_{55}^{\left(l\right)}{q}_{1}^{l+2}{u}_{1}\right]\left(\delta \left({q}_{1}=ka\right)-\delta \left({q}_{1}=kb\right)\right)\right\}\end{aligned}$$
$$\begin{aligned}{{}_{j}^{m}A}_{32}^{l}=& \frac{1}{{\left(kH\right)}^{l}}\left\{\left[n\left({C}_{23}^{\left(l\right)}+{C}_{44}^{\left(l\right)}\right){q}_{1}^{l+1}{u}_{2}\right] \pi \left(ka, kb\right)\right\}\end{aligned}$$
$$\begin{aligned}{{}_{j}^{m}A}_{32}^{l}=& \frac{1}{{\left(kH\right)}^{l}}\left\{\left[{C}_{55}^{\left(l\right)}{q}_{1}^{l+2}{{u}^{{^{\prime}}{^{\prime}}}}_{3}-{n}^{2}{C}_{44}^{\left(l\right)}{q}_{1}^{l}{u}_{3}-{C}_{33}^{\left(l\right)}{q}_{1}^{l+2}{u}_{3}+\left(1+l\right){C}_{55}^{\left(l\right)}{q}_{1}^{l+1}{{u}^{^{\prime}}}_{3}\right] \pi \left(ka, kb\right)\right.\\ &\left.+\left[{C}_{55}^{\left(l\right)}{q}_{1}^{l+2}{{u}^{^{\prime}}}_{3}\right]\left(\delta \left({q}_{1}=ka\right)-\delta \left({q}_{1}=kb\right)\right)\right\}\end{aligned}$$
$${M}_{m,j}^{l}=-\frac{{\rho }^{\left(l\right)}}{{\left(kH\right)}^{l}}{q}_{1}^{l+2}\pi \left(ka, kb\right)$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Raghib, R., Naciri, I., Khalfi, H. et al. Vibration analysis of a multilayer functionally graded cylinder with effects of graded-index and boundary conditions. Acta Mech 234, 3933–3953 (2023). https://doi.org/10.1007/s00707-023-03590-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-023-03590-7

Keywords

Search

Navigation