Modelling architected beam using a nonlocal derivative-free shear deformable beam theory

Abstract

It has been well established that the internal length scale related to the cell size plays a critical role in the response of architected structures. It this paper, a Volterra derivative-based approach for deriving nonlocal continuum laws directly from an energy expression without involving spatial derivatives of the displacement is proposed. A major aspect of the work is the introduction of a nonlocal derivative-free directionality term, which recovers the classical deformation gradient in the infinitesimal limit. The proposed directionality term avoids issues with correspondences under nonsymmetric conditions (such a unequal distribution of points that cause trouble with conventional correspondence-based approaches in peridynamics). Using this approach, we derive a nonlocal version of a shear deformable beam model in the form of integro-differential equations. As an application, buckling analysis of architected beams with different core shapes is performed. In this context, we also provide a physical basis for the consideration of energy for nonaffine (local bending) deformation. This removes the need for additional energy in an ad hoc manner towards suppressing zero-energy modes. The numerical results demonstrate that the proposed framework can accurately estimate the critical buckling load for a beam in comparison to 3-D simulations at a small fraction of the cost and computational time. Efficacy of the framework is demonstrated by analysing the responses of a deformable beam under different loads and boundary conditions.

Appendix A localization of derivative-free deformation gradient G

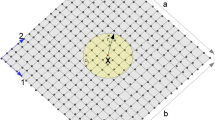
Here, we demonstrate that the derivative-free nonlocal directionality term approaches the classical deformation gradient in the infinitesimal limit. Let us assume sufficient smoothness of the field such that the displacement at a material point Y, in the neighbourhood of X, can be approximated using a truncated Taylor expansion as:

$$\begin{aligned} \begin{aligned} {u(Y)\approx u(X)+\triangledown (u,X)(Y-X)}, \end{aligned} \end{aligned}$$

(A1)

where ${\triangledown }$ is the classical gradient operator. The average stretch around X may also be approximated in a similar way.

$$\begin{aligned} \begin{aligned} {\bar{u}(Y) \approx u(X)+\triangledown (u,X)(\overline{Y-X})}. \end{aligned} \end{aligned}$$

(A2)

The nonlocal derivative-free deformation gradient is expressed as:

$$\begin{aligned} \begin{aligned} G(u,X)&=I+\hat{G}(u,X)\\ {}&=I+\left[ \int _{\Omega _x}\left( u-\bar{u}\right) \left( Y-\bar{Y}\right) ^T dY\right] \left[ \int _{\Omega _x}\left( Y-\bar{Y}\right) \left( Y-\bar{Y}\right) ^T dY\right] ^{-1}, \end{aligned} \end{aligned}$$

(A3)

where I is the identity tensor. Replacing the terms in Eq. (A3) with those given in Eqs. (A1) and (A2), we get,

$$\begin{aligned} {G}&\approx {I+\left[ \int _{\Omega _x}\left( u(X)+\triangledown (u,X)(Y-X)-(u(X)+\triangledown (u,X)(\overline{Y-X}))\right) \left( Y-\bar{Y}\right) ^TdY\right] }.\nonumber \\&\quad {I+\left[ \int _{\Omega _X} (Y-\bar{Y})(Y-\bar{Y})^T dY\right] ^{-1}}\nonumber \\&= {I+\left[ \int _{\Omega _x}\triangledown (u,X)(Y-X-\overline{Y-X})\left( Y-\bar{Y}\right) ^TdY\right] } {\left[ \int _{\Omega _X} (Y-\bar{Y})(Y-\bar{Y})^TdY\right] ^{-1}}\nonumber \\&= {I+\triangledown (u,X)\left[ \int _{\Omega _x}(Y-X-\bar{Y}-\bar{X})\left( Y-\bar{Y}\right) ^TdY\right] } {\left[ \int _{\Omega _X} (Y-\bar{Y})(Y-\bar{Y})^T dY\right] ^{-1}}\nonumber \\&= {I+\triangledown (u,X)\left[ \int _{\Omega _x}(Y-\bar{Y})\left( Y-\bar{Y}\right) ^TdY\right] } {\left[ \int _{\Omega _X} (Y-\bar{Y})(Y-\bar{Y})^T dY\right] ^{-1}}\nonumber \\&= {I+\triangledown (u,X)}\nonumber \\&= {F}. \end{aligned}$$

(A4)