Skip to main content
SpringerLink
Log in

Localized bending waves along the edge of a piezoelectric sandwich plate

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

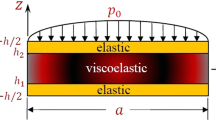
This paper deals with the propagation of bending waves along the free edge of a piezoelectric sandwich plate. The structure consists of a piezoelectric layer sandwiched between two metal layers. The first-order Zig-Zag approximation for in-plane displacements through the thickness of each layer is used. Interfacial continuity of the displacement and the transverse shear stress between the piezoelectric layer and the metal layer is ensured which is very important and also experienced by layered structures. The number of independent unknown variables is reduced from 14 to 4 by using the interfacial continuity and the zero shear stresses conditions at the top and bottom surfaces. The governing equations and corresponding boundary conditions are derived using Hamiltonian principle. The dispersion relations for electrically open and shorted boundary conditions imposed at the edge of the semi-infinite piezoelectric sandwich plate are obtained. The effects of electrical edge condition, layer thickness ratio and material property on dispersion characteristics of the localized bending waves are discussed. The numerical results show that the electrical edge condition has significant influence on dispersion property compared to edge wave in a piezoelectric single-layer plate. The phase velocity and the localization of bending edge wave significantly depend on the thickness of metal layer, and a thick metal layer can result in a high wave velocity and a strong localization. The phase velocity of bending wave is positively related to the velocities of classical Rayleigh surface wave in piezoelectric half-space and metal half-space under plane strain.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Konenkov, Y.K.: A Rayleigh-type flexural wave. Soviet Phys. Acoust. 6(1), 122–123 (1960)

    MathSciNet  Google Scholar 

  2. Lawrie, J.B., Kaplunov, J.: Edge waves and resonance on elastic structures: an overview. Math. Mech. Solids 17(1), 4–16 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  3. Thurston, R.N., Mckenna, J.: Flexural acoustic waves along the edge of a plate. IEEE Trans. Son. Ultrason. 21(4), 296–297 (1974)

    Article  Google Scholar 

  4. Norris, A.N.: Flexural edge waves. J. Sound Vib. 171(4), 571–573 (1994)

    Article  MATH  Google Scholar 

  5. Thompson, I., Abrahams, I.D., Norris, A.N.: On the existence of flexural edge waves on thin orthotropic plates. J. Acoust. Soc. Am. 112(5), 1756–1765 (2002)

    Article  Google Scholar 

  6. Zakharov, D.D., Becker, W.: Rayleigh type bending waves in anisotropic media. J. Sound Vib. 261(5), 805–818 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  7. Fu, Y.B.: Existence and uniqueness of edge waves in a generally anisotropic elastic plate. Q. J. Mech. Appl. Mech. 56(4), 605–616 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Liu, G.R., Tani, J., Ohyoshi, T., et al.: Characteristics of surface wave propagation along the edge of an anisotropic laminated semi-infinite plate. Wave Motion 13(3), 243–251 (1991)

    Article  MATH  Google Scholar 

  9. Fu, Y.B., Brookes, D.W.: Edge waves in asymmetrically laminated plates. J. Mech. Phys. Solids 54(1), 1–21 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Lu, P., Chen, H.B., Lee, H.P., et al.: Further studies on edge waves in anisotropic elastic plates. Int. J. Solids Struct. 44(7–8), 2192–2208 (2007)

    Article  MATH  Google Scholar 

  11. Lagasse, P.E., Oliner, A.A.: Acoustic flexural mode on a ridge of semi-infinite height. Electron. Lett. 12(1), 11–13 (1976)

    Article  Google Scholar 

  12. Norris, A.N., Krylov, V.V., Abrahams, I.D.: Flexural edge waves and comments on ‘A new bending wave solution for the classical plate equation’ [J Acoust Soc Am 104: 2220–2222 (1998)]. J. Acoust. Soc. Am. 107(3), 1781–1784 (2000)

    Article  Google Scholar 

  13. Piliposian, G.T., Belubekyan, M.V., Ghazaryan, K.B.: Localized bending waves in a transversely isotropic plate. J. Sound Vib. 329(17), 3596–3605 (2010)

    Article  Google Scholar 

  14. Alzaidi, A.S., Kaplunov, J., Prikazchikova, L.: Elastic bending wave on the edge of a semi-infinite plate reinforced by a strip plate. Math. Mech. Solids 24(10), 3319–3330 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  15. Nie, G.Q., Dai, B., Liu, J.X., Zhang, L.L.: Bending waves in a semi-infinite piezoelectric plate with edge coated by a metal strip plate. Wave Motion 103(4), 102731 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  16. Belubekyan, M.V., Ghazaryan, K., Marzocca, P., Cormier, C.: Localized bending waves in a rib-reinforced elastic orthotropic plate. J. Appl. Mech. 74, 169–171 (2007)

    Article  MATH  Google Scholar 

  17. Alzaidi, A.S., Kaplunov, J., Prikazchikova, L.: The edge bending wave on a plate reinforced by a beam (L). J. Acoust. Soc. Am. 146(2), 1061–1064 (2019)

    Article  MATH  Google Scholar 

  18. Kaplunov, J., Prikazchikov, D.A., Rogerson, G.A., Lashab, M.I.: The edge wave on an elastically supported Kirchhoff plate. J. Acoust. Soc. Am. 136(4), 1487–1490 (2014)

    Article  Google Scholar 

  19. Kaplunov, J., Prikazchikov, D.A., Rogerson, G.A.: Edge bending wave on a thin elastic plate resting on a Winkler foundation. Proc. R. Soc. A Math. Phys. Eng. Sci. 472, 20160178 (2016)

    MathSciNet  MATH  Google Scholar 

  20. Althobaiti, S.N., Nikonov, A., Prikazchikov, D.: Explicit model for bending edge wave on an elastic orthotropic plate supported by the Winkler–Fuss foundation. J. Mech. Mater. Struct. 16(4), 543–554 (2021)

    Article  MathSciNet  Google Scholar 

  21. Althobaiti, S., Hawwa, M.A.: Flexural edge waves in a thick piezoelectric film resting on a Winkler foundation. Crystals 12, 640 (2022)

    Article  Google Scholar 

  22. Kaplunov, J., Nobili, A.: The edge waves on a Kirchhoff plate bilaterally supported by a two-parameter elastic foundation. J. Sound Vib. 23(12), 2014–2022 (2017)

    MathSciNet  MATH  Google Scholar 

  23. Abrahams, I.D., Norris, A.N.: On the Existence of flexural edge waves on submerged elastic plates. Proc. R. Soc. A Math. Phys. Eng. Sci. 456, 1559–1582 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  24. Kaplunov, J., Prikazchikova, L., Alkinidri, M.: Antiplane shear of an asymmetric sandwich plate. Continuum Mech. Thermodyn. 33, 1247–1262 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  25. Wilde, M.V., Surova, M.Y., Sergeeva, N.V.: Asymptotically correct boundary conditions for the higher-order theory of plate bending. Math. Mech. Solids 27(9), 1813–1854 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  26. Piliposian, G.T., Ghazaryan, K.B.: Localized bending vibrations of piezoelectric plates. Waves Random Complex Med. 21(3), 418–433 (2011)

    Article  MATH  Google Scholar 

  27. Nie, G.Q., Lei, Z.Y., Liu, J.X., Zhang, L.L.: Bending waves localized along the edge of a semi-infinite piezoelectric plate with orthogonal symmetry. Front. Mater. 9, 1031538 (2022)

    Article  Google Scholar 

  28. Carrera, E.: Historical review of zig-zag theories for multilayered plates and shells. Appl. Mech. Rev. 56(3), 287–308 (2003)

    Article  Google Scholar 

  29. Kapuria, S., Nath, J.K.: Coupled global-local and zigzag-local laminate theories for dynamic analysis of piezoelectric laminated plates. J. Sound Vib. 332, 306–325 (2013)

    Article  Google Scholar 

  30. Ye, R.C., Tian, A.L., Chen, Y.M., et al.: Sound transmission characteristics of a composite sandwich plate using multi-layer first-order zigzag theory. Thin-Walled Struct. 179, 109607 (2022)

    Article  Google Scholar 

  31. Keshtegar, B., Motezaker, M., Kolahchi, R., et al.: Wave propagation and vibration responses in porous smart nanocomposite sandwich beam resting on Kerr foundation considering structural damping. Thin-Walled Struct. 154, 106820 (2020)

    Article  Google Scholar 

  32. Nath, J.K., Mishra, B.B., Das, T.: Improved electromechanical response in laminated piezoelectric plates using a zigzag theory. J. Aerosp. Eng. 34(6), 04021083 (2021)

    Article  Google Scholar 

  33. Quek, S.T., Wang, Q.: On dispersion relations in piezoelectric coupled-plate structures. Smart Mater. Struct. 9(6), 859–867 (2000)

    Article  Google Scholar 

  34. Ke, L.L., Liu, C., Wang, Y.S.: Free vibration of nonlocal piezoelectric nanoplates under various boundary conditions. Physica E 66, 93–106 (2015)

    Article  Google Scholar 

  35. Reddy, J.N.: Energy Principles and Variational Methods in Applied Mechanics. Wiley, Hoboken (2017)

    Google Scholar 

  36. Luan, G.D., Zhang, J.D., Wang, R.Q.: Piezoelectric Transducer and Arrays (revised edition) (in Chinese). Peking University Press, Beijing (2005)

    Google Scholar 

  37. Rose, J.L.: Ultrasonic Waves in Solid Media. Cambridge University Press, Cambridge (1999)

    Google Scholar 

Download references

Acknowledgements

This study is supported by the National Natural Science Foundation of China (No. 11872041) and the Top-notch Young Talent Program of Hebei Province Education Department of China (No. BJK2022055).

Author information

Authors and Affiliations

  1. State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang, 050043, China

    Guoquan Nie & Jinxi Liu

  2. School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang, 050043, China

    Guoquan Nie

  3. Department of Engineering Mechanics, Shijiazhuang Tiedao University, Shijiazhuang, 050043, China

    Jiapeng Zhuang & Lele Zhang

Authors
  1. Guoquan Nie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiapeng Zhuang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jinxi Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lele Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lele Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

Expressions of the axial forces, shearing force, bending moments and twisting moment in Eq. (14) are given by

$$\left\{ \begin{aligned} & N_{x}^{l} = \int_{{ - h^{l} - h^{m} /2}}^{{ - h^{m} /2}} {\left( {\lambda^{l} + 2\mu^{l} } \right)\left( {\frac{\partial U}{{\partial x}} - z\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right){\text{d}}z} = h^{l} \left( {\lambda^{l} + 2\mu^{l} } \right)\left( {\frac{\partial U}{{\partial x}} + \frac{{h^{l} + h^{m} }}{2}\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) \quad \; \\ & N_{x}^{u} = \int_{{h^{m} /2}}^{{h^{u} + h^{m} /2}} {\left( {\lambda^{u} + 2\mu^{u} } \right)\left( {\frac{\partial U}{{\partial x}} - z\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right){\text{d}}z} = h^{u} \left( {\lambda^{u} + 2\mu^{u} } \right)\left( {\frac{\partial U}{{\partial x}} - \frac{{h^{u} + h^{m} }}{2}\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) \quad \; \\ & N_{x}^{m} = \int_{{ - h^{m} /2}}^{{h^{m} /2}} {c_{11}^{{}} \left( {\frac{\partial U}{{\partial x}} - z\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) + c_{12}^{{}} \left( {\frac{\partial V}{{\partial y}} - z\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) + e_{31}^{{}} \beta \sin \left( {\beta z} \right)\Phi {\text{d}}z} = h^{m} \left( {c_{11} \frac{\partial U}{{\partial x}} + c_{12} \frac{\partial V}{{\partial y}}} \right) \\ \end{aligned} \right.$$
$$\left\{ \begin{aligned} & N_{y}^{l} = \int_{{ - h^{l} - h^{m} /2}}^{{ - h^{m} /2}} {\left( {\lambda^{l} + 2\mu^{l} } \right)\left( {\frac{\partial V}{{\partial y}} - z\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right){\text{d}}z} = h^{l} \left( {\lambda^{l} + 2\mu^{l} } \right)\left( {\frac{\partial V}{{\partial y}} + \frac{{h^{l} + h^{m} }}{2}\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) \quad \; \\ & N_{y}^{u} = \int_{{h^{m} /2}}^{{h^{u} + h^{m} /2}} {\left( {\lambda^{u} + 2\mu^{u} } \right)\left( {\frac{\partial V}{{\partial y}} - z\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right){\text{d}}z} = h^{u} \left( {\lambda^{u} + 2\mu^{u} } \right)\left( {\frac{\partial V}{{\partial y}} - \frac{{h^{u} + h{}^{m}}}{2}\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) \quad \; \\ & N_{y}^{m} = \int_{{ - h^{m} /2}}^{{h^{m} /2}} {c_{12}^{{}} \left( {\frac{\partial U}{{\partial x}} - z\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) + c_{11}^{{}} \left( {\frac{\partial V}{{\partial y}} - z\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) + e_{31}^{{}} \beta \sin \left( {\beta z} \right)\Phi {\text{d}}z} = h^{m} \left( {c_{12} \frac{\partial U}{{\partial x}} + c_{11} \frac{\partial V}{{\partial y}}} \right) \\ \end{aligned} \right.$$
$$\left\{ \begin{gathered} N_{xy}^{l} = \int_{{ - h^{l} - h^{m} /2}}^{{ - h^{m} /2}} {\mu^{l} \left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}} - 2z\frac{{\partial^{2} W}}{\partial x\partial y}} \right){\text{d}}z} = h^{l} \mu^{l} \left[ {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}} + \left( {h^{l} + h^{m} } \right)\frac{{\partial^{2} W}}{\partial x\partial y}} \right] \\ N_{xy}^{u} = \int_{{h^{m} /2}}^{{h^{u} + h^{m} /2}} {\mu^{u} \left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}} - 2z\frac{{\partial^{2} W}}{\partial x\partial y}} \right){\text{d}}z} = h^{u} \mu^{u} \left[ {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}} - \left( {h^{u} + h^{m} } \right)\frac{{\partial^{2} W}}{\partial x\partial y}} \right] \\ N_{xy}^{m} = \int_{{ - h^{m} /2}}^{{h^{m} /2}} {c_{66}^{{}} \left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}} - 2z\frac{{\partial^{2} W}}{\partial x\partial y}} \right){\text{d}}z} = h^{m} c_{66} \left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}}} \right) \qquad \qquad\qquad\qquad \qquad \\ \end{gathered} \right.$$
$$\left\{ \begin{aligned} M_{x}^{l} = \; & \int_{{ - h^{l} - h^{m} /2}}^{{ - h^{m} /2}} {\left[ {z\left( {\lambda^{l} + 2\mu^{l} } \right)\left( {\frac{\partial U}{{\partial x}} - z\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right)} \right]{\text{d}}z} \\ \quad = \; & - h^{l} \left( {\lambda^{l} + 2\mu^{l} } \right)\left[ {\frac{{h^{l} + h^{m} }}{2}\frac{\partial U}{{\partial x}} + \frac{{3h^{m2} + 6h^{m} h^{l} + 4h^{l2} }}{12}\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right] \\ M_{x}^{u} = \; & \int_{{h^{m} /2}}^{{h + h^{m} /2^{u} }} {\left[ {z\left( {\lambda^{u} + 2\mu^{u} } \right)\left( {\frac{\partial U}{{\partial x}} - z\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right)} \right]{\text{d}}z} \\ \quad = \; & h^{u} \left( {\lambda^{u} + 2\mu^{u} } \right)\left[ {\frac{{h^{u} + h^{m} }}{2}\frac{\partial U}{{\partial x}} - \frac{{3h^{m2} + 6h^{m} h^{u} + 4h^{u2} }}{12}\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right] \\ M_{x}^{m} = \; & \int_{{ - h^{m} /2}}^{{h^{m} /2}} {zc_{11}^{{}} \left( {\frac{\partial U}{{\partial x}} - z\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) + zc_{12}^{{}} \left( {\frac{\partial V}{{\partial y}} - z\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) + ze_{31}^{{}} \beta \sin \left( {\beta z} \right)\Phi {\text{d}}z} \\ \quad = \; & - \frac{{h^{m3} }}{12}\left( {c_{11} \frac{{\partial^{2} W}}{{\partial x^{2} }} + c_{12} \frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) + \frac{{2h^{m} e_{31} }}{\pi }\Phi \\ \end{aligned} \right.$$
$$\left\{ \begin{aligned} & M_{y}^{l} = \int_{{ - h^{l} - h^{m} /2}}^{{ - h^{m} /2}} {z\left( {\lambda^{l} + 2\mu^{l} } \right)\left( {\frac{\partial V}{{\partial y}} - z\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right){\text{d}}z} \quad \; \\ &\quad = - h^{l} \left( {\lambda^{l} + 2\mu^{l} } \right)\left[ {\frac{{h^{l} + h^{m} }}{2}\frac{\partial V}{{\partial y}} + \frac{{3h^{m2} + 6h^{m} h^{l} + 4h^{l2} }}{12}\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right] \\ & M_{y}^{u} = \int_{{h^{m} /2}}^{{h^{u} + h^{m} /2}} {\left[ {z\left( {\lambda^{u} + 2\mu^{u} } \right)\left( {\frac{\partial V}{{\partial y}} - z\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right)} \right]{\text{d}}z} \quad \; \\ & \quad = h^{u} \left( {\lambda^{u} + 2\mu^{u} } \right)\left[ {\frac{{h^{u} + h^{m} }}{2}\frac{\partial V}{{\partial y}} - \frac{{3h^{m2} + 6h^{m} h^{u} + 4h^{u2} }}{12}\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right] \\ & M_{y}^{m} = \int_{{ - h^{m} /2}}^{{h^{m} /2}} {zc_{12}^{{}} \left( {\frac{\partial U}{{\partial x}} - z\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right) + zc_{11}^{{}} \left( {\frac{\partial V}{{\partial y}} - z\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) + ze_{31}^{{}} \beta \sin \left( {\beta z} \right)\Phi {\text{d}}z} \\ &\quad = - \frac{{h^{m3} }}{12}\left( {c_{12} \frac{{\partial^{2} W}}{{\partial x^{2} }} + c_{11} \frac{{\partial^{2} W}}{{\partial y^{2} }}} \right) + \frac{{2e_{31} h^{m} }}{\pi }\Phi \\ \end{aligned} \right.$$
$$\left\{ \begin{aligned} M_{xy}^{l} = \; & \int_{{ - h^{l} - h^{m} /2}}^{{ - h^{m} /2}} {z\mu^{l} \left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}} - 2z\frac{{\partial^{2} W}}{\partial x\partial y}} \right){\text{d}}z} \\ = \; & - h^{l} \mu^{l} \left[ {\frac{{h^{l} + h^{m} }}{2}\left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}}} \right) + \frac{{3h^{m2} + 6h^{m} h^{l} + 4h^{l2} }}{12}\frac{{\partial^{2} W}}{\partial x\partial y}} \right] \\ M_{xy}^{u} = \; & \int_{{h^{m} /2}}^{{h^{u} + h^{m} /2}} {z\mu^{u} \left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}} - 2z\frac{{\partial^{2} W}}{\partial x\partial y}} \right){\text{d}}z} \\ = \; & h^{u} \mu^{u} \left[ {\frac{{h^{u} + h^{m} }}{2}\left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}}} \right) - \frac{{3h^{m2} + 6h^{m} h^{u} + 4h^{u2} }}{12}\frac{{\partial^{2} W}}{\partial x\partial y}} \right] \\ M_{xy}^{m} = \; & \int_{{ - h^{m} /2}}^{{h^{m} /2}} {zc_{66}^{{}} \left( {\frac{\partial U}{{\partial y}} + \frac{\partial V}{{\partial x}} - 2z\frac{{\partial^{2} W}}{\partial x\partial y}} \right){\text{d}}z} = - \frac{{c_{66} h^{m3} }}{6}\frac{{\partial^{2} W}}{\partial x\partial y} \\ \end{aligned} \right.$$

where λu, μu and λl, μl are the Lame constants of upper and lower metal layer, respectively.

Appendix B

The nonzero elements of matrix Q in Eq. (24) are given by.

\(\begin{aligned} Q_{11} = \; & n^{l} \left( {\lambda^{l} + 2\mu^{l} } \right) + n^{u} \left( {\lambda^{u} + 2\mu^{u} } \right) + c_{11} \\ & + p^{2} \left( {n^{l} \mu^{l} + n^{u} \mu^{u} + c_{66} } \right) - 2c^{2} \left( {n^{l} \rho^{l} + n^{u} \rho^{u} + \rho^{m} } \right) \\ \end{aligned}\),

\(Q_{12} = p\left( {n^{l} \mu^{l} + n^{u} \mu^{u} + c_{12} + c_{66} } \right)\),

\(\begin{aligned} Q_{13} = \; & \xi \left( {\lambda^{l} + 2\mu^{l} } \right)\frac{{n^{l} \left( {n^{l} + 1} \right)}}{2} - \xi \left( {\lambda^{u} + 2\mu^{u} } \right)\frac{{n^{u} \left( {n^{u} + 1} \right)}}{2} \\ & + \xi p^{2} n^{l} \left( {n^{l} + 1} \right)\mu^{l} - \xi p^{2} n^{u} \left( {n^{u} + 1} \right)\mu^{u} + \xi c^{2} n^{u} \left( {n^{u} + 1} \right)\rho^{u} - \xi c^{2} n^{l} \left( {n^{l} + 1} \right)\rho^{l} \\ \end{aligned}\),

\(Q_{21} = p\left( {n^{l} \mu^{l} + n^{u} \mu^{u} + c_{12} + c_{66} } \right)\),

\(\begin{aligned} Q_{22} = \; & p^{2} n^{l} \left( {\lambda^{l} + 2\mu^{l} } \right) + p^{2} n^{u} \left( {\lambda^{u} + 2\mu^{u} } \right) \\ & + p^{2} c_{11} + n^{l} \mu^{l} + n^{u} \mu^{u} + c_{66} - 2c^{2} \left( {n^{l} \rho^{l} + n^{u} \rho^{u} + \rho^{m} } \right) \\ \end{aligned}\),

\(\begin{aligned} Q_{23} = \; & \xi p^{3} \left( {\lambda^{l} + 2\mu^{l} } \right)\frac{{n^{l} \left( {n^{l} + 1} \right)}}{2} - \xi p^{3} \left( {\lambda^{u} + 2\mu^{u} } \right)\frac{{n^{u} \left( {n^{u} + 1} \right)}}{2} \\ & + \xi pn^{l} \left( {n^{l} + 1} \right)\mu^{l} - \xi pn^{u} \left( {n^{u} + 1} \right)\mu^{u} + p\xi c^{2} n^{u} \left( {n^{u} + 1} \right)\rho^{u} - p\xi c^{2} n^{l} \left( {n^{l} + 1} \right)\rho^{l} \\ \end{aligned}\),

\(\begin{aligned} Q_{31} = \; & - \left( {\lambda^{l} + 2\mu^{l} } \right)\frac{{n^{l} \left( {n^{l} + 1} \right)}}{2} + \left( {\lambda^{u} + 2\mu^{u} } \right)\frac{{n^{u} \left( {n^{u} + 1} \right)}}{2} \\ & - p^{2} \mu^{l} \frac{{n^{l} \left( {n^{l} + 1} \right)}}{2} + p^{2} \mu^{u} \frac{{n^{u} \left( {n^{u} + 1} \right)}}{2} - 2c^{2} n^{u} \left( {n^{u} + 1} \right)\rho^{u} - 2c^{2} n^{l} \left( {n^{l} + 1} \right)\rho^{l} \\ \end{aligned}\),

\(\begin{aligned} Q_{32} = \; & - p^{3} \left( {\lambda^{l} + 2\mu^{l} } \right)\frac{{n^{l} \left( {n^{l} + 1} \right)}}{2} + p^{3} \left( {\lambda^{u} + 2\mu^{u} } \right)\frac{{n^{u} \left( {n^{u} + 1} \right)}}{2} \\ & - p\mu^{l} \frac{{n^{l} \left( {n^{l} + 1} \right)}}{2} + p\mu^{u} \frac{{n^{u} \left( {n^{u} + 1} \right)}}{2} - pc^{2} n^{u} \left( {n^{u} + 1} \right)\rho^{u} + pc^{2} n^{l} \left( {n^{l} + 1} \right)\rho^{l} \\ \end{aligned}\),

\(\begin{aligned} Q_{33} = \; & - \xi \left( {1 + p^{4} } \right)\left( {\lambda^{l} + 2\mu^{l} } \right)\frac{{3n^{l} + 6n^{l2} + 4n^{l3} }}{12} \\ & - \xi \left( {1 + p^{4} } \right)\left( {\lambda^{u} + 2\mu^{u} } \right)\frac{{3n^{u} + 6n^{u2} + 4n^{u3} }}{12} - \xi \left( {1 + p^{4} } \right)\frac{{\left( {c_{11} + c_{12} } \right)}}{12} + \\ & - \xi p^{2} \mu^{l} \frac{{3n^{l} + 6n^{l2} + 4n^{l3} }}{12} - \xi p^{2} \mu^{u} \frac{{3n^{u} + 6n^{u2} + 4n^{u3} }}{12} - \xi p^{2} \frac{{c_{66} }}{6} \\ & + 2\xi^{ - 1} c^{2} \left( {n^{l} \rho^{l} + n^{u} \rho^{u} + \rho^{m} } \right) + \xi \left( {c^{2} + p^{2} c^{2} } \right)\rho^{l} \frac{{3n^{l} + 6n^{l2} + 4n^{l3} }}{6} \\ & + \xi \left( {c^{2} + p^{2} c^{2} } \right)\rho^{u} \frac{{3n^{u} + 6n^{u2} + 4n^{u3} }}{6} + \xi \left( {c^{2} + p^{2} c^{2} } \right)\frac{{\rho^{m} }}{6} \\ \end{aligned}\),

\(Q_{34} = - 2\xi^{ - 2} \left( {1 + p^{2} } \right)\frac{{e_{31} }}{\pi } \,\), \(Q_{43} = 2\left( {1 + p^{2} } \right)\frac{{e_{31}^{{}} }}{\pi }\), \(Q_{44} = - \left( {1 + p^{2} } \right)\frac{{s_{11}^{{}} }}{2} - \xi^{ - 2} \pi^{2} \frac{{s_{33}^{{}} }}{2}\).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nie, G., Zhuang, J., Liu, J. et al. Localized bending waves along the edge of a piezoelectric sandwich plate. Acta Mech 234, 3483–3498 (2023). https://doi.org/10.1007/s00707-023-03571-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-023-03571-w

Search

Navigation