On the stability of bodies suspended asymmetrically with an inelastic rope

Abstract

The stability of a body suspended asymmetrically by means of an inelastic rope is investigated. The rope is attached to the body at two points and passed over a frictionless hook or a nail in the vertical plane. The equilibrium points of the system and their stability are described as a function of the rope length, the distance of the attachment points and the position of the center of mass. Depending on the choice of the parameters, one, two or three equilibrium positions exist: their structural change manifests itself in the form of cusp bifurcations of co-dimension two, which is determined in exact analytical form.

1 Introduction

Bodies suspended by a rope and fixed at two points are common in both everyday life and engineering practice. A picture hanging on a wall and lifting a body by a crane are typical examples of this method of fixation (see Fig. 1). In case of a short rope passed over a hook (or nail) without further fixation at the hook, the body hanging on it might hang tilted to the side. As a result of environmental effects (vibrations, rope stretching, temperature fluctuations or creep, etc.), it can sometimes also happen that the body that has otherwise been motionless for a long time suddenly completely changes the direction of its suspension. In the case of pictures, this is purely aesthetically annoying, but in the case of heavy bodies moved by a crane, the sudden change in position can cause damage, accidents or even endanger lives. Due to the risk of the above described catastrophe phenomenon, it is prohibited to attach hanging loads to a crane this way.

The article is based on the model published in [1]. Taking into account the possible asymmetry of the body, the extended model presented in this article is suitable for the mathematical description of the suspension of arbitrarily shaped rigid bodies. The methods applied in the article are similar to the methods used to investigate the stability of blocks floating on water surface, which problem also depends on many geometrical and physical parameters at the same time [2]. Similarity in the modeling approach can also be found with the methods applied for the description of water-filled containers, able to turn around a fixed axis [3, 4]. The stability of ships is an active research topic with direct applications in naval design problems [5,6,7]. Despite being a simpler problem with easy experimental verification, the problem of a body suspended by a rope received much less attention in the literature [1].

The findings presented in the current paper have direct constructional implications. They can be utilized to avoid catastrophe when designing safe suspensions of the above kind. It also has relevance in the design of tensegrity structures where bi-stability is actually desired [8].

The paper is structured as follows: in Sect. 2 the setup of the model is presented, followed by Sect. 3, where the equation describing the equilibrium positions is derived. In Sect. 4, graphical solution of the above equation is given and the stability analysis of the equilibrium positions is performed. In Sect. 5, the catastrophe surface and the region in the parameter plane where multiple equilibrium points coexist are calculated in exact closed form.

Section 6 summarizes the findings and gives scope for future research.

2 Model setting

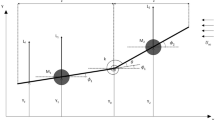
Let us investigate the problem setting depicted in Fig. 1. An inelastic rope of length 2c is fixed to the rigid body of mass m at the points $F_1$ and $F_2$ of distance 2a from each other. The rope is passed over the point $P'$ that represents the hook (or nail). Would the point lie at the middle of the rope (point P) so would the suspension be symmetric; this point P is represented relative to the body in Fig. 1.

Without loss of generality, it is sufficient to consider the problem in two dimensions, in the plane defined by the points $P',F_1$ and $F_2$. The coordinate system $(x',y')$ is bound to the direction of the gravitational force, such that the $y'$ axis is parallel to it. Let us define a second, new coordinate system, fixed to the suspended object, such that its center, O, is at the halfway between $F_1$ and $F_2$ with x axis parallel to $\vec {r}_{F_1F_2}$ and y axis parallel to $\vec {r}_{OP}$. The position of the center of mass, C, is a further important parameter in the problem setting. At the equilibrium, it lies in the vertical plane of the $x'-y'$ coordinate system. Let us denote its position by $(-e,-d)$ in the newly defined coordinate system O(x, y), where e and d refer to the eccentricity of the center of mass and its depth, respectively. For convenience, we introduce the dependent parameter

$$\begin{aligned} h:=\sqrt{c^2-a^2} \end{aligned}$$

(1)

which is just the distance between P and O. As already described in [1], the feasible positions of the suspension point $P'(x,y)$ are located at a half ellipse where $y_{P'}\ge 0$. The focal points of the ellipse are just $F_1$ and $F_2$. Its major and minor axes have lengths c and h, respectively.

Fig. 1

Problem setting of an asymmetrically suspended body

The angle $\varphi '$ between the y axis and the vector $\vec {r}_{CP'}$ represents the skewness of the suspended body in the ground based coordinates $O'(x',y')$, since at the static hanging position, $\vec {r}_{CP'}$ is parallel to the direction of the gravitational force. $\varphi '$ is not used in further investigations, only serves to facilitate the characterization of the body’s position in the plane.

3 Finding the equilibrium positions

The equilibrium positions corresponding to $P'(x,y)$ of the hanging body can be found by means of the local extrema of the body’s potential energy given by

$$\begin{aligned} U=-mg |\vec {r}_{CP'} |. \end{aligned}$$

(2)

In case of a minimum of U, the equilibrium is stable, in case of a maximum, it is unstable. The only factor influencing stability is the distance $l:=|\vec {r}_{CP'} |$, which guarantees a stable equilibrium if it has a local maximum due to the negative sign in Eq. (2).

The position vector of the center of mass from the suspension point is given by

$$\begin{aligned} \vec {r}_{CP'}= \begin{pmatrix} e+x\\ d+y \end{pmatrix}, \end{aligned}$$

(3)

leading to

$$\begin{aligned} l(x)=\sqrt{(e+x)^2+(d+y(x))^2} \end{aligned}$$

(4)

where y can be expressed by x from the condition that the rope is in tension, and consequently, the point $P'$ is located on the ellipse defined by

$$\begin{aligned} \frac{x^2}{c^2}+\frac{y^2}{h^2}=1 \quad \Rightarrow \quad y(x)=h\sqrt{1-\frac{x^2}{c^2}}. \end{aligned}$$

(5)

An extremum of the potential function U(x) exists when, according to Eq. (4), it holds that an extremum of the always positive l(x) exists, i.e., where an extremum of its square is taken. Being $l^2(x)$ a continuous function, it has a local extremum in $x \in (-c,c)$ if

$$\begin{aligned} \frac{\text {d}}{\text {d}x}l^2(x) =2(e+x)+2 \left( d+y(x) \right) y'(x) \overset{!}{=}0, \end{aligned}$$

(6)

where

$$\begin{aligned} y'(x)=-\frac{hx}{c^2 \sqrt{1-\frac{x^2}{c^2}}}. \end{aligned}$$

(7)

Inserting Eqs. (5) and (7) into Eq. (6), we have

$$\begin{aligned} e+x-\frac{ d+h\sqrt{1-\frac{x^2}{c^2}}}{c^2 \sqrt{1-\frac{x^2}{c^2}}}hx=0. \end{aligned}$$

(8)

Using Eq. (1) and rearranging the equation, we find

$$\begin{aligned} \left( e+\frac{a^2}{c^2}x \right) \sqrt{ 1-\frac{x^2}{c^2}}=\frac{hd}{c^2}x. \end{aligned}$$

(9)

Non-dimensionalization of x is performed by introducing

$$\begin{aligned} X:=\frac{x}{c}, \end{aligned}$$

(10)

which after insertion into Eq. (9) and multiplication both sides of the equation with $c/a^2$ yields

$$\begin{aligned} \left( \frac{ec}{a^2}+X \right) \sqrt{1-X^2}=\frac{hd}{a^2}X. \end{aligned}$$

(11)

The four parameters a, c, d and e finally can be reduced to the two independent parameters

$$\begin{aligned} D:=\frac{hd}{a^2}, \quad E:=\frac{ec}{a^2}, \end{aligned}$$

(12)

denoting the dimensionless depth and eccentricity of the center of mass, respectively.¹ Then, Eq. (11) can be written in the form

$$\begin{aligned} (E+X)\sqrt{1-X^2}=D X, \end{aligned}$$

(13)

the solutions of which present the equilibrium positions of the suspended body, where the potential function U(x) has extrema. If $E=0$, then the trivial solution of Eq. (13) is the real root $X_1=0$ that always exists, and if $D<1$, there exist two further real roots given by $X_{2,3}=\pm \sqrt{1-D^2}$. In case of $E\ne 0$, that is with some eccentricity $e\ne 0$, it is not so simple to find the roots of Eq. (13), since the roots of a non-reducible quartic polynomial have to be found. To carry out a graphical interpretation of the problem, we divide both sides of the equation by $E+X$ leading to

$$\begin{aligned} \sqrt{1-X^2}=D\frac{X}{X+E}. \end{aligned}$$

(14)

4 Graphical solution and stability analysis

Although it would be possible to solve Eq. (14) in closed form, since it is equivalent to a fourth-degree polynomial, we evade this step, as the solution is very intricate and not necessary for the stability analysis. Instead, let us construct a qualitative picture of the solutions graphically. This way, the overall effects of the parameters D and E become visible.

Fig. 2

Graphical representation of the solutions of Eq. (14). The left hand side of the equation is an upper semi-circle, while the right hand side is a hyperbola with asymptotes at $-E$ and D. Based on the value of D and E, the upper semi-circle and the hyperbola have either 1, 2 (double root, when touching) or 3 distinct, real solutions ($X_1, X_2$ and $X_3$). The hyperbola also has an intersection with the lower semi-circle yielding the extraneous solution $X^{*}$

Based on Fig. 2, there are three different cases regarding the number of the distinct real solutions of Eq. (14):

• 1 real solution, if the values of D and E are sufficiently large. The body possesses one resting position.

• 2 real solutions, if one branch of the hyperbola intersects while the other branch just touches the upper semi-circle. This case is a bifurcation point.

• 3 real solutions, when there are three equilibrium positions for sufficiently small values of D and E.

It is important to note that since the hyperbola always crosses the origin, there exists at least one solution.

In order to determine whether an equilibrium point is stable or not, we can check the sign of the second derivative of $l^2(x)$ evaluated at the root $x_k$ in question. We get

$$\begin{aligned} \frac{\text {d}^2}{\text {d}x^2}l^2(x)=2 \left( \frac{a^2}{c^2}- \frac{chd}{ (c^2-x^2)^{3/2}} \right) . \end{aligned}$$

(15)

The equilibrium point $x_k$ is stable if $l^2(x)$ has a local maximum there, which can be found out by checking the sign of the second derivative at the equilibrium point. After division by $2a^2 /c^2$ and using Eq. (12), the condition of the existence of a maximum in dimensionless form is

$$\begin{aligned} 1- D^{2/3} < X_k^2, \end{aligned}$$

(16)

which means that the potential function (2) has a minimum, that is, the equilibrium at $X_k$ is stable.

Based on the geometry, it is clear that if Eq. (14) has only one real solution, that must be stable. In case of three solutions, Eq. (16) implies that the middle one $X_1$ must be unstable. This can be proven by contradiction, assuming $X_1$ is stable. Due to the geometry, we have $X_1^2<X_2^2$ and $X_1^2<X_3^2$; thus, $X_2$ and $X_3$ fulfill condition (16) as well, which implies that all three solutions are stable. But this is clearly a topological contradiction. Thus, in case of three equilibrium positions $X_1$ is always unstable and $X_{2,3}$ are stable.

5 Finding the catastrophe surface in closed form

In the next step, we would like to determine whether Eq. (13) has one, two or three real roots depending on the combinations of the parameters D and E. Thus, we can also obtain two regions in the E–D parameter plane resulting in one or three real roots, divided by a curve, which corresponds to the case of two real roots. To simplify Eq. (13) further, we need to take the square of both sides

$$\begin{aligned} (X+E)^2 \left( 1-X^2\right) =D^2 X^2. \end{aligned}$$

(17)

Yet, doing so, unwillingly we produce a false root $X^*$ (cf. Fig 2) of Eq. (17). When taking the square, not only the intersections of the hyperbolas and the upper semi-circle are calculated, but also the intersection with the lower semi-circle leading always to $X^*$. Thus, we consider two different scenarios: Eq. (17) has either 2 or 4 real roots, including the false root as well. Expanding Eq. (17), we have

$$\begin{aligned} X^4+2E X^3+(E^2+D^2-1) X^2-2E X-E^2=0. \end{aligned}$$

(18)

Equation (18) has two symmetries, axial symmetry to the E–X plane and central symmetry to the D axis. The axial symmetry is due to $D^2$, which is the only occurrence of the dimensionless depth variable D and the axial symmetry is due to the fact that the equation remains valid under simultaneous sign change in E and X.

We focus on the finding of the parameter combinations of D and E which describes the limiting case that separates the regions of 2 and 4 real roots. When a transition takes place, at least two roots are identical. Such structural changes in the solutions of a polynomial are related to the polynomial’s discriminant $\Delta$ [9] which becomes zero at the transition. It suffices to calculate the parametric curve

$$\begin{aligned} \Delta (D,E)=0. \end{aligned}$$

(19)

The discriminant of a general fourth-degree polynomial of the form

$$\begin{aligned} p_4X^4+p_3X^3+p_2X^2+p_1X+p_0=0 \end{aligned}$$

(20)

is given by formula [9]

$$\begin{aligned} \begin{aligned} \Delta&=256p_4^3p_0^3-192p_4^2p_3p_1p_0^2-128p_4^2p_2^2p_0^2+144p_4^2p_2p_1^2p_0-27p_4^2p_1^4\\&\quad +144p_4p_3^2p_2p_0^2-6p_4p_3^2p_1^2p_0-80p_4p_3p_2p_1^3+16p_4p_2^4p_0-4p_4p_2^3p_1^2\\&\quad -27p_3^4p_0^2+18p_3^3p_2p_1p_0-4p_3^3p_1^3-4p_3^2p_2^3p_0+p_3^2p_2^2p_1^2. \end{aligned} \end{aligned}$$

(21)

Fig. 3

Projection of the catastrophe surface on the plane of the parameters E and D defined by $E^{2/3}+D^{2/3}<1$. In the white region, only one equilibrium position exists, which is stable. In the gray region, three equilibrium positions exist (stable–unstable–stable). The pink region $D<0$ is not of interest due to the instability of such constructions (color figure online)

In our case, this means

$$\begin{aligned} p_4=1, \quad p_3=2E, \quad p_2=E^2+D^2-1,\quad p_1=-2E,\quad p_0=-E^2, \end{aligned}$$

(22)

which inserted into condition (19) yields

$$\begin{aligned} \begin{aligned}&-E^8D^2-3E^6D^4+3E^6D^2-3E^4D^6-21E^4D^4-3E^4D^2\\&\quad -E^2D^8+3E^2D^6-3E^2D^4+E^2D^2=0. \end{aligned} \end{aligned}$$

(23)

Rearranging and simplifying the terms results in

$$\begin{aligned} E^{2/3}+D^{2/3}=1. \end{aligned}$$

(24)

This is the equation of the so called astroid (see Fig. 3) [10]. This curve is obtained, if one rolls a circle of radius 1/4 along the inner side of the unit circle and follows the path of a chosen point on the rolling circle’s circumference. In this context, it presents those lines along the catastrophe surface where a fold bifurcation takes place and the number of equilibrium positions changes from 1 to 3.

A graphical representation of the function l(X) is shown in Fig. 4 together with its extrema. In Fig. 5, we can see the plots of the roots of Eq. (13) for various fixed values of E. The supercritical pitchfork bifurcation for $E=0$ falls apart into a fold bifurcation and a regular, always stable solution for the eccentricity $E\ne 0$.

Fig. 4

The distance l(X) of the center of the mass C from the suspension point $P'$ with parameters $a=0.6$, $d=0.31275$, $c=1$, ($h=0.8$) for three different values of the eccentricity $e=\lbrace 0.018, 0.036, 0.054 \rbrace$. The corresponding non-dimensional values are $X=x$, $D\approx 0.695$ and $E= \lbrace 0.05,0.1,0.15 \rbrace$. The markers represent the equilibrium points. With growing eccentricity, the stable equilibrium position on the left disappears. The value $E_c = 0.1$ is the limiting case, where the two left hand side equilibrium points meet and disappear for $E>E_c$

Fig. 5

The roots of Eq. (13), $X_i$ depicted against D for fixed values of E. The root in the middle is unstable (- - -), while the roots on the side are stable (—). When having $E=0.1$, the fold is at $D \approx 0.695$ (

), for which parameter choice the rope length is illustrated in Fig. 4 (color figure online)

6 Conclusions

The stability of the equilibrium points of a rigid body which is suspended asymmetrically at two points by a single rope passed frictionless over a hook (or a nail) has been investigated in gravitational space. It has been shown that the four parameters describing the model, such as the distance of the fixations, rope length, the vertical and the horizontal position of the body’s center of mass, can be reduced to two dimensionless parameters suitable to describe the behavior of the system regarding stability. Under the variation of the above parameters, the number of equilibrium points changes. This structural change is categorized as a cusp bifurcation of co-dimension two. Under the variation of the non-dimensional parameter D and without eccentricity, the remaining one-parameter bifurcation is supercritical pitchfork, which for nonzero eccentricity of the suspension falls apart into a regular branch and into a fold. In the other hand, under the variation of E, the bifurcations are always folds.

In safety-critical applications, the parameter region where multiple equilibrium points exist at the same time is to be avoided as the transposition from one resting position to the other one, even for a slight perturbation, might be a sudden and unexpected movement possibly endangering lives and material goods [11]. Such a dangerous scenario is, for example, when a person is climbing up or down on a suspended heavy object slowly causing the variation of the depth of the whole system’s center of mass. In case of climbing down, the current equilibrium solution might disappear due to the slowly increasing value of D and a sudden, dangerous jump occurs to the remaining stable equilibrium. In case of climbing upwards, the stable equilibrium starts shifting continuously while a pair of stable and unstable equilibrium positions also appears. Similarly dangerous situations occur when the center of mass of a suspended container gets shifted downwards or upwards due to rain [3], for example. Analogous scenarios take place if a person (or an animal, see Fig. 6) moves horizontally on the suspended object causing the change of the eccentricity E. In the paper, the easily applicable condition $D^{2/3}+E^{2/3}>1$ has been derived to check whether a given setup is safety-critical or not.

Fig. 6

Cat walking on a suspended beam. Due to the cat’s movement, the system’s center of mass also changes. If the cat gets close to the other side of the beam, the actual equilibrium position might disappear leading to a sudden movement of the beam

An interesting question that might give scope for further research regards the effect of an external force acting on the body. In case of multiple equilibrium points, a dynamic external force could also cause transition from one local minimum of the potential energy to another local minimum, which dynamic process is called escape [11]. This problem generalization might find applications in the construction of safe suspensions on floating cranes, in the shifting of goods by crane in windy weather, or large tanks with fluid streaming out of them, in which case the excitation is a follower force.

Appendix

Fig. 7

The surface of equilibrium positions depicted in the E–D–X-space. The curve along which the bifurcation points are located is given in red (color figure online)

The surface of equilibrium positions $X_i$ as a multi-valued function of the non-dimensional parameters E and D is investigated in the appendix.

The original problem’s stable equilibrium positions are given by the maxima of Eq. (4) which might include also boundary points at $X=\pm 1$. The unstable equilibrium positions are given, however, only by the local minima of Eq. (4) excluding the boundary values. Thus, the set of all equilibrium positions is given by the solutions of Eq. (13) and by the values $X=\pm 1$, in case they are local maxima. It is easy to check that for $D>0$, l(X) always has local minima at the boundary points $X=\pm 1$, and thus, these points are not equilibrium positions. For $D<0$, l(X) has always local maxima at $X=\pm 1$, and thus, these points are stable equilibria. The surface of all equilibrium positions depicted in the plane of the non-dimensional parameters E and D is shown in Fig. 7. We can observe the Whitney fold cusp bifurcation centered at $(E,D)=(0,1)$.

Due to the change to Eq. (18), the problem’s solution gains an extra, spurious solution. Not considering the stable boundaries in case of $D<0$, the equilibrium positions, including the spurious one, are given by the real solutions of Eq. (18) and are depicted in Fig. 8.

Fig. 8

The surface of the solutions of Eq. (18) depicted in the E–D–X space. The curve along which the bifurcation points are located is given in red (color figure online)

The projection of the bifurcation points of Eq. (18) on the plane of the non-dimensional parameters, i.e., the astroid (c.f. Figure 3), resembles of that found in case of Zeeman’s catastrophe machine that has also 4 cusps [12, 13]. It should be noted, however, that by the removal of the spurious solution, three cusps disappear. The one at $(E,D)=(0,-1)$ gets entirely lost and the ones at $(E,D)=(\pm 1,0)$ become simple folds.