Free vibration and nonlinear dynamic behaviors of the imperfect smart electric magnetic FG-laminated composite panel in a hygrothermal environments

Abstract

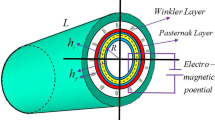
Piezoelectric and piezomagnetic layers are known to enhance material properties and increase load capacity. However, most studies focused on the effects of mechanical and thermal loads on these structures. This work aimed to investigate the complex external condition of uniformed load, thermal load, moisture parameter and electric–magnetic potentials of the smart electric magnetic panel using an analytical approach. The core of the panel is made of graphene platelets, and the two outer layers consist of barium titanate (BaTiO₃) and cobalt ferric oxide (CoFe₂O₄). The Ready’s first-order shear deformation and Hamilton’s theory are proposed to govern the basic equation. After that, the stress function is introduced, and then apply the Galerkin method to determine the natural frequency and dynamic response of the panel. The final chapter analyzes the relationship between the natural frequency and amplitude of the electromagnetic panel with simplified assumptions. The numerical results are highlighted using the Runge–Kutta method, including the influence of the piezoelectric outer layer, geometry parameters, imperfection, elastic foundations, graphene volume fraction, thermal loads and electric and magnetic fields of the electromagnetic panel. The reliability of this computational theory is validated by other publications. In addition, the new influence of electrical and magnetic field parameters on the panel’s natural frequency is also emphasized.

Appendices

Appendix 1

$$\begin{aligned} & \overline{{A_{11} }} = A_{11}^{f} - \frac{{\left( {A_{13}^{f} } \right)^{2} }}{{A_{33}^{f} }},\overline{{A_{12} }} = A_{12}^{f} - \frac{{A_{13}^{f} A_{23}^{f} }}{{A_{33}^{f} }},\overline{{A_{22} }} = A_{22}^{f} - \frac{{\left( {A_{23}^{f} } \right)^{2} }}{{A_{33}^{f} }},\overline{{A_{44} }} = A_{44}^{f} ,\overline{{A_{55} }} = A_{55}^{f} , \\ & \overline{{A_{66} }} = A_{66}^{f} ,\overline{{e_{31} }} = e_{31}^{f} - \frac{{A_{13}^{f} e_{33}^{f} }}{{A_{33}^{f} }},\overline{{e_{32} }} = e_{32}^{f} - \frac{{A_{23}^{f} e_{33}^{f} }}{{A_{33}^{f} }},\overline{{e_{15} }} = e_{15}^{f} ,\overline{{e_{24} }} = e_{24}^{f} ,\overline{{q_{31} }} = q_{31}^{f} - \frac{{A_{13}^{f} q_{33}^{f} }}{{A_{33}^{f} }}, \\ & \overline{{q_{32} }} = q_{32}^{f} - \frac{{A_{23}^{f} q_{33}^{f} }}{{A_{33}^{f} }},\overline{{q_{15} }} = q_{15}^{f} ,\overline{{q_{24} }} = q_{24}^{f} ,\overline{{\mu_{11} }} = \mu_{11}^{f} ,\overline{{\mu_{22} }} = \mu_{22}^{f} ,\overline{{\mu_{33} }} = \mu_{33}^{f} + \frac{{\left( {q_{33}^{f} } \right)^{2} }}{{A_{33}^{f} }}, \\ & \overline{{\eta_{11} }} = \eta_{11}^{f} ,\overline{{\eta_{22} }} = \eta_{22}^{f} ,\overline{{\eta_{33} }} = \eta_{33}^{f} + \frac{{\left( {e_{33}^{f} } \right)^{2} }}{{A_{33}^{f} }},\overline{{m_{11} }} = m_{11}^{f} ,\overline{{m_{22} }} = m_{22}^{f} ,\overline{{m_{33} }} = m_{33}^{f} + \frac{{e_{33}^{f} q_{33}^{f} }}{{A_{33}^{f} }}, \\ & \overline{{\alpha_{1} }} = \alpha_{1}^{f} - \frac{{A_{13}^{f} \alpha_{3}^{f} }}{{A_{33}^{f} }},\overline{{\alpha_{2} }} = \alpha_{2}^{f} - \frac{{A_{23}^{f} \alpha_{3}^{f} }}{{A_{33}^{f} }},\overline{{\beta_{1} }} = \beta_{1}^{f} - \frac{{A_{13}^{f} \beta_{3}^{f} }}{{A_{33}^{f} }},\overline{{\beta_{2} }} = \beta_{2}^{f} - \frac{{A_{23}^{f} \beta_{3}^{f} }}{{A_{33}^{f} }}, \\ & \overline{{p_{1} }} = p_{1}^{f} ,\overline{{p_{2} }} = p_{2}^{f} ,\overline{{p_{3} }} = p_{3}^{f} + \frac{{e_{33}^{f} \alpha_{33}^{f} }}{{A_{33}^{f} }},\overline{{\lambda_{1} }} = \lambda_{1}^{f} ,\overline{{\lambda_{2} }} = \lambda_{2}^{f} ,\overline{{\lambda_{3} }} = \lambda_{3}^{f} + \frac{{q_{33}^{f} \alpha_{33}^{f} }}{{A_{33}^{f} }}, \\ & \overline{{\chi_{1} }} = \chi_{1}^{f} ,\overline{{\chi_{2} }} = \chi_{2}^{f} ,\overline{{\chi_{3} }} = \chi_{3}^{f} + \frac{{e_{33}^{f} \beta_{33}^{f} }}{{A_{33}^{f} }},\overline{{\zeta_{1} }} = \zeta_{1}^{f} ,\overline{{\zeta_{2} }} = \zeta_{2}^{f} ,\overline{{\zeta_{3} }} = \zeta_{3}^{f} + \frac{{q_{33}^{f} \beta_{33}^{f} }}{{A_{33}^{f} }}. \\ \end{aligned}$$

Appendix 2

$$\begin{aligned} & \left( {A_{ij} ,B_{ij} ,P_{ij} } \right) = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\overline{{A_{ij} }} } \left( {1,z,z^{2} } \right){\text{d}}z + \sum\limits_{k = 1}^{n} {\int\limits_{k - 1}^{k} {Q_{ij}^{c} } } \left( {1,z,z^{2} } \right){\text{d}}z + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\overline{{A_{ij} }} } \left( {1,z,z^{2} } \right){\text{d}}z,\quad ij = 11,12,\,22, \\ & A_{44} = K\left[ {\int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\frac{1}{2}\overline{{A_{44} }} } {\text{d}}z + \sum\limits_{k = 1}^{n} {\int\limits_{k - 1}^{k} {Q_{44}^{c} } } {\text{d}}z + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\frac{1}{2}\overline{{A_{44} }} } dz} \right],\, \\ & A_{55} = K\left[ {\int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\frac{1}{2}\overline{{A_{55} }} } {\text{d}}z + \sum\limits_{k = 1}^{n} {\int\limits_{k - 1}^{k} {Q_{55}^{c} } } {\text{d}}z + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\frac{1}{2}\overline{{A_{55} }} } {\text{d}}z} \right],\, \\ & \left( {A_{66} ,B_{66} ,P_{66} } \right) = \left[ {\int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\frac{1}{2}\overline{{A_{66} }} } \left( {1,z,z^{2} } \right){\text{d}}z + \sum\limits_{k = 1}^{n} {\int\limits_{k - 1}^{k} {Q_{66}^{c} } } \left( {1,z,z^{2} } \right){\text{d}}z + \int\limits_{{h_{c} /2}}^{{h_{c} /2 + h_{f} }} {\frac{1}{2}\overline{{A_{66} }} } \left( {1,z,z^{2} } \right){\text{d}}z} \right] \\ & \left( {\Gamma_{1} ,\,\Gamma_{3} } \right) = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\overline{{e_{31} }} \kappa \sin \left( {\kappa z} \right)} \left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{e_{31} }} \kappa \sin \left( {\kappa z} \right)\left( {1,z} \right)} {\text{d}}z, \\ & \left( {\Gamma_{2} ,\,\Gamma_{4} } \right) = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\overline{{e_{32} }} \kappa \sin \left( {\kappa z} \right)} \left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{e_{32} }} \kappa \sin \left( {\kappa z} \right)\left( {1,z} \right)} {\text{d}}z, \\ & \left( {H_{1} ,H_{3} } \right) = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\overline{{q_{31} }} \kappa \sin \left( {\kappa z} \right)} \left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{q_{31} }} \kappa \sin \left( {\kappa z} \right)\left( {1,z} \right)} {\text{d}}z, \\ & \left( {H_{2} ,H_{4} } \right) = \int\limits_{{ - h_{f} - h_{c} /2}}^{{ - h_{c} /2}} {\overline{{q_{32} }} \kappa \sin \left( {\kappa z} \right)} \left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{q_{32} }} \kappa \sin \left( {\kappa z} \right)\left( {1,z} \right)} {\text{d}}z, \\ & \left( {D_{1} ,\,D_{3} } \right) = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{\alpha_{1}^{{}} }} \left( {1,z} \right){\text{d}}z + } \sum\limits_{k = 1}^{n} {\int\limits_{{h_{k - 1} }}^{{h_{k} }} {\alpha \left( {Q_{11}^{c} + Q_{12}^{c} } \right)} } \left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{\alpha_{1}^{{}} }} \left( {1,z} \right){\text{d}}z} , \\ & \left( {D_{2} ,\,D_{4} } \right) = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{\alpha_{2}^{{}} }} \left( {1,z} \right){\text{d}}z + } \sum\limits_{k = 1}^{n} {\int\limits_{{h_{k - 1} }}^{{h_{k} }} {\alpha \left( {Q_{12}^{c} + Q_{22}^{c} } \right)} } \left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{\alpha_{2}^{{}} }} \left( {1,z} \right){\text{d}}z} ,\, \\ & \left( {E_{1} ,\,E_{3} } \right) = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{\beta_{1}^{{}} }} \left( {1,z} \right){\text{d}}z + } \sum\limits_{k = 1}^{n} {\int\limits_{{h_{k - 1} }}^{{h_{k} }} {\beta_{c} } } \left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{\beta_{1}^{{}} }} \left( {1,z} \right){\text{d}}z} \\ & \left( {E_{2} ,\,E_{4} } \right) = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{\beta_{2}^{{}} }} \left( {1,z} \right){\text{d}}z + } \sum\limits_{k = 1}^{n} {\int\limits_{{h_{k - 1} }}^{{h_{k} }} {\beta_{c} } } \left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{\beta_{2}^{{}} }} \left( {1,z} \right){\text{d}}z} \\ \end{aligned}$$

$$\begin{aligned} & \left( {F_{1} ,\,F_{3} } \right) = \left( {\int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{e_{31} }} } \frac{2}{h}\left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{e_{31}^{{}} }} \frac{2}{h}\left( {1,z} \right){\text{d}}z} } \right) \\ & \left( {F_{2} ,\,F_{4} } \right) = \left( {\int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{e_{32} }} } \frac{2}{h}\left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{e_{32}^{{}} }} \frac{2}{h}\left( {1,z} \right){\text{d}}z} } \right) \\ & \left( {G_{1} ,\,G_{3} } \right) = 2\left( {\int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{q_{31} }} } \frac{2}{h}\left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{q_{31}^{{}} }} \frac{2}{h}\left( {1,z} \right){\text{d}}z} } \right), \\ & \left( {G_{2} ,\,G_{4} } \right) = 2\left( {\int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{q_{32} }} } \frac{2}{h}\left( {1,z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{q_{32}^{{}} }} \frac{2}{h}\left( {1,z} \right){\text{d}}z} } \right), \\ & {\rm T}_{mn} = - K\left[ {\int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} \frac{1}{2} \overline{{e_{mn} }} \cos \left( {\kappa z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\frac{1}{2}\overline{{e_{mn} }} \cos \left( {\kappa z} \right)} {\text{d}}z} \right],\quad mn = 15,24 \\ & {\rm O}_{mn} = - K\left[ {\int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} \frac{1}{2} \overline{{q_{mn} }} \cos \left( {\kappa z} \right){\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\frac{1}{2}\overline{{q_{mn} }} \cos \left( {\kappa z} \right)} {\text{d}}z} \right],\quad mn = 15,24 \\ \end{aligned}$$

Appendix 3

$$\begin{aligned} & J_{11} \left( w \right) = A_{55} \frac{{\partial^{2} w}}{{\partial x^{2} }} + A_{44} \frac{{\partial^{2} w}}{{\partial y^{2} }} - k_{1} w + k_{2} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right),J_{12} \left( {\phi_{x} } \right) = A_{55} \frac{{\partial \phi_{x} }}{\partial x},J_{13} \left( {\phi_{y} } \right) = A_{44} \frac{{\partial \phi_{y} }}{\partial y}, \\ & J_{14} \left( f \right) = \frac{1}{{R_{x} }}\frac{{\partial^{2} f}}{{\partial x^{2} }},J_{15} \left( \Phi \right) = \left( {T_{15} \frac{{\partial^{2} }}{{\partial x^{2} }} + T_{24} \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)\Phi ,J_{16} \left( \Psi \right) = \left( {O_{15} \frac{{\partial^{2} }}{{\partial x^{2} }} + O_{24} \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)\Psi , \\ & O\left( {w,f} \right) = \frac{{\partial^{2} f}}{{\partial y^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} - 2\frac{{\partial^{2} f}}{\partial x\partial y}\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }}, \\ \end{aligned}$$

$$\begin{aligned} O^{*} (w^{*} ,f) & = A_{55} \frac{{\partial^{2} w^{*} }}{{\partial x^{2} }} + A_{44} \frac{{\partial^{2} w^{*} }}{{\partial y^{2} }} + \left( {\frac{{\partial^{2} f}}{{\partial y^{2} }}\frac{{\partial^{2} w^{*} }}{{\partial x^{2} }} - 2\frac{{\partial^{2} f}}{\partial x\partial y}\frac{{\partial^{2} w^{*} }}{\partial x\partial y} + \frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} w^{*} }}{{\partial y^{2} }}} \right), \\ J_{21} (w^{*} ) & = - A_{55} \frac{\partial w*}{{\partial x}}, \\ J_{31} (w^{*} ) & = - A_{44} \frac{{\partial w^{*} }}{\partial y}, \\ \end{aligned}$$

Appendix 4

$$\begin{aligned} & l_{0} = - \left( {A_{55} \lambda_{m}^{2} + A_{44} \delta_{n}^{2} } \right), \\ & l_{1} = - \frac{1}{{R_{x} }}\lambda_{m}^{2} \overline{{I_{1} }} , \\ & l_{2} = - A_{55} \lambda_{m} - \frac{1}{{R_{x} }}\lambda_{m}^{2} \overline{{I_{2} }} ,\,l_{3} = - A_{44} \delta_{n} - \frac{1}{{R_{x} }}\lambda_{m}^{2} \overline{{I_{3} }} , \\ & l_{4} = - \left( {T_{15} \lambda_{m}^{2} + T_{24} \delta_{n}^{2} } \right) - \frac{1}{{R_{x} }}\lambda_{m}^{2} \overline{{I_{4} }} ,\,l_{5} = - \left( {O_{15} \lambda_{m}^{2} + O_{24} \delta_{n}^{2} } \right) - \frac{1}{{R_{x} }}\lambda_{m}^{2} \overline{{I_{5} }} , \\ & l_{6} = l_{0} - \left( {N_{x0} \lambda_{m}^{2} + N_{y0} \delta_{n}^{2} } \right) \\ & l_{7} = \frac{{32\lambda_{m}^{2} \delta_{n}^{2} }}{{3mn\pi^{2} }}\overline{{I_{1} }} ,\,\,l_{8} = \frac{{32\lambda_{m}^{2} \delta_{n}^{2} }}{{3mn\pi^{2} }}\overline{{I_{2} }} ,\,l_{9} = \frac{{32\lambda_{m}^{2} \delta_{n}^{2} }}{{3mn\pi^{2} }}\overline{{I_{3} }} , \\ & l_{10} = \frac{{32\lambda_{m}^{2} \delta_{n}^{2} }}{{3mn\pi^{2} }}\overline{{I_{4} }} ,\,\,l_{11} = \frac{{32\lambda_{m}^{2} \delta_{n}^{2} }}{{3mn\pi^{2} }}\overline{{I_{5} }} ,\,l_{12} = \frac{{2\delta_{n}^{2} }}{{3mn\pi^{2} \overline{{B_{2} }} R_{x} }}, \\ & l_{13} = - \frac{{\delta_{n}^{4} }}{{16\overline{{B_{2} }} }} - \frac{{\lambda_{m}^{4} }}{{16\overline{{A_{1} }} }},\,\,l_{14} = \frac{16}{{mn\pi^{2} }}, \\ \end{aligned}$$

$$\begin{aligned} & l_{21} = \left( { - D_{1} \delta_{n}^{2} + D_{10} \delta_{n}^{2} - D_{2} \lambda_{m}^{2} } \right)\lambda_{m} \overline{{I_{1} }} , \\ & l_{22} = - \left( {D_{3} \lambda_{m}^{2} + H_{10} \delta_{n}^{2} + A_{55} } \right) + \left( { - D_{1} \delta_{n}^{2} + D_{10} \delta_{n}^{2} - D_{2} \lambda_{m}^{2} } \right)\lambda_{m} \overline{{I_{2} }} , \\ & l_{23} = - \left( {D_{4} + H_{10} } \right)\lambda_{m} \delta_{n} + \left( { - D_{1} \delta_{n}^{2} + D_{10} \delta_{n}^{2} - D_{2} \lambda_{m}^{2} } \right)\lambda_{m} \overline{{I_{3} }} , \\ & l_{24} = \left( {D_{5} - T_{15} } \right)\lambda_{m} - \left( {D_{1} \delta_{n}^{2} - D_{10} \delta_{n}^{2} + D_{2} \lambda_{m}^{2} } \right)\lambda_{m} \overline{{I_{4} }} , \\ & l_{25} = \left( {D_{6} - O_{15} } \right)\lambda_{m} - \left( {D_{1} \delta_{n}^{2} - D_{10} \delta_{n}^{2} + D_{2} \lambda_{m}^{2} } \right)\lambda_{m} \overline{{I_{5} }} , \\ & l_{26} = - A_{55} \lambda_{m} ,l_{27} = \frac{{8\lambda_{m} \delta_{n}^{2} D_{2} }}{{3mn\pi^{2} \overline{{B_{2} }} }}, \\ \end{aligned}$$

$$\begin{aligned} & l_{31} = \left( {D_{10} \lambda_{m}^{2} - H_{1} \delta_{n}^{2} - H_{2} \lambda_{m}^{2} } \right)\delta_{n} \overline{{I_{1} }} , \\ & l_{32} = - \left( {H_{3} + H_{10} } \right)\lambda_{m} \delta_{n} + \left( {D_{10} \lambda_{m}^{2} - H_{1} \delta_{n}^{2} - H_{2} \lambda_{m}^{2} } \right)\delta_{n} \overline{{I_{2} }} , \\ & l_{33} = - \left( {H_{4} \delta_{n}^{2} + H_{10} \lambda_{m}^{2} + A_{44} } \right) + \left( {D_{10} \lambda_{m}^{2} - H_{1} \delta_{n}^{2} - H_{2} \lambda_{m}^{2} } \right)\delta_{n} \overline{{I_{3} }} , \\ & l_{34} = \left[ {\left( {H_{5} - T_{24} } \right) + \left( {D_{10} \lambda_{m}^{2} - H_{1} \delta_{n}^{2} - H_{2} \lambda_{m}^{2} } \right)\overline{{I_{4} }} } \right]\delta_{n} , \\ & l_{35} = \left[ {\left( {H_{6} - O_{24} } \right) + \left( {D_{10} \lambda_{m}^{2} - H_{1} \delta_{n}^{2} - H_{2} \lambda_{m}^{2} } \right)\overline{{I_{5} }} } \right]\delta_{n} , \\ & l_{36} = - A_{44} \delta_{n} , \\ & l_{37} = \frac{{8\lambda_{m}^{2} \delta_{n} H_{1} }}{{3mn\pi^{2} \overline{{A_{1} }} }}, \\ \end{aligned}$$

Appendix 5

$$\begin{aligned} & \overline{{a_{1} }} = \left( { - a_{1} \lambda_{m}^{2} - a_{2} \delta_{n}^{2} } \right) - \left( {a_{9} \lambda_{m}^{2} + a_{10} \delta_{n}^{2} } \right)\overline{{I_{1} }} , \\ & \overline{{a_{2} }} = - a_{3} \lambda_{m} - \left( {a_{9} \lambda_{m}^{2} + a_{10} \delta_{n}^{2} } \right)\overline{{I_{2} }} , \\ & \overline{{a_{3} }} = - a_{4} \delta_{n} - \left( {a_{9} \lambda_{m}^{2} + a_{10} \delta_{n}^{2} } \right)\overline{{I_{3} }} , \\ & \overline{{a_{4} }} = - \left( {a_{5} \lambda_{m}^{2} + a_{6} \delta_{n}^{2} - a_{11} } \right) - \left( {a_{9} \lambda_{m}^{2} + a_{10} \delta_{n}^{2} } \right)\overline{{I_{4} }} , \\ & \overline{{a_{5} }} = - \left( {a_{7} \lambda_{m}^{2} + a_{8} \delta_{n}^{2} - a_{12} } \right) - \left( {a_{9} \lambda_{m}^{2} + a_{10} \delta_{n}^{2} } \right)\overline{{I_{5} }} , \\ & \overline{{a_{6} }} = \frac{{2\delta_{n}^{2} a_{9} }}{{3mn\pi^{2} \overline{{B_{2} }} }} + \frac{{2\lambda_{m}^{2} a_{10} }}{{3mn\pi^{2} \overline{{A_{1} }} }}, \\ & \overline{{a_{7} }} = \frac{16}{{mn\pi^{2} }},\,\,\overline{{a_{8} }} = \frac{16}{{mn\pi^{2} }}a_{13} , \\ & \overline{{a_{9} }} = \frac{16}{{mn\pi^{2} }}a_{14} ,\,\overline{{a_{10} }} = \frac{16}{{mn\pi^{2} }}a_{15} ,\,\overline{{a_{11} }} = \frac{16}{{mn\pi^{2} }}a_{16} , \\ & \overline{{a_{21} }} = \left( { - a_{21} \lambda_{m}^{2} - a_{22} \delta_{n}^{2} } \right) - \left( {a_{29} \lambda_{m}^{2} + a_{30} \delta_{n}^{2} } \right)\overline{{I_{1} }} , \\ & \overline{{a_{22} }} = - a_{23} \lambda_{m} - \left( {a_{29} \lambda_{m}^{2} + a_{30} \delta_{n}^{2} } \right)\overline{{I_{2} }} , \\ & \overline{{a_{23} }} = - a_{24} \delta_{n} - \left( {a_{29} \lambda_{m}^{2} + a_{30} \delta_{n}^{2} } \right)\overline{{I_{3} }} , \\ & \overline{{a_{24} }} = - \left( {a_{25} \lambda_{m}^{2} + a_{26} \delta_{n}^{2} - a_{31} } \right) - \left( {a_{29} \lambda_{m}^{2} + a_{30} \delta_{n}^{2} } \right)\overline{{I_{4} }} , \\ & \overline{{a_{25} }} = - \left( {a_{27} \lambda_{m}^{2} + a_{28} \delta_{n}^{2} - a_{32} } \right) - \left( {a_{29} \lambda_{m}^{2} + a_{30} \delta_{n}^{2} } \right)\overline{{I_{5} }} , \\ & \overline{{a_{26} }} = \frac{{2\delta_{n}^{2} a_{29} }}{{3mn\pi^{2} \overline{{B_{2} }} }} + \frac{{2\lambda_{m}^{2} a_{30} }}{{3mn\pi^{2} \overline{{A_{1} }} }},\overline{{a_{27} }} = \frac{16}{{mn\pi^{2} }},\,\overline{{a_{28} }} = \frac{16}{{mn\pi^{2} }}a_{33} , \\ & \overline{{a_{29} }} = \frac{16}{{mn\pi^{2} }}a_{34} ,\,\,\overline{{a_{30} }} = \frac{16}{{mn\pi^{2} }}a_{35} ,\,\overline{{a_{31} }} = \frac{16}{{mn\pi^{2} }}a_{36} , \\ \end{aligned}$$

$$\begin{aligned} a_{1} &= \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{e_{15}^{{}} }} \cos (\kappa z)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{e_{15}^{{}} }} \cos (\kappa z)} {\text{d}}z, \\ a_{2} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{e_{24} }} \cos (\kappa z)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{e_{24} }} \cos (\kappa z)} {\text{d}}z, \\ a_{3} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left[ {\overline{{e_{15}^{{}} }} \cos (\kappa z) + \left( {\overline{{A_{3} }} \overline{{e_{31} }} + \overline{{B_{3} }} \overline{{e_{32} }} + \overline{{e_{31} }} z} \right)\kappa \sin (\kappa z)} \right]} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left[ {\overline{{e_{15}^{{}} }} \cos (\kappa z) + \left( {\overline{{A_{3} }} \overline{{e_{31} }} + \overline{{B_{3} }} \overline{{e_{32} }} + \overline{{e_{31} }} z} \right)\kappa \sin (\kappa z)} \right]} {\text{d}}z, \\ a_{4} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left[ {\overline{{e_{24} }} \cos (\kappa z) + \left( {\overline{{A_{4} }} \overline{{e_{31} }} + \overline{{B_{4} }} \overline{{e_{32} }} + \overline{{e_{32} }} z} \right)\kappa \sin (\kappa z)} \right]} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left[ {\overline{{e_{24} }} \cos (\kappa z) + \left( {\overline{{A_{4} }} \overline{{e_{31} }} + \overline{{B_{4} }} \overline{{e_{32} }} + \overline{{e_{32} }} z} \right)\kappa \sin (\kappa z)} \right]} {\text{d}}z, \\ a_{5} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{\eta_{11} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{\eta_{11} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z, \\ a_{6} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{\eta_{22}^{{}} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{\eta_{22}^{{}} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z, \\ a_{7} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{m_{11}^{{}} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{m_{11}^{{}} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z, \\ a_{8} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{m_{22}^{{}} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{m_{22}^{{}} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z, \\ \end{aligned}$$

$$\begin{aligned} a_{9} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{2} }} \overline{{e_{31} }} + \overline{{B_{2} }} \overline{{e_{32} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{2} }} \overline{{e_{31} }} + \overline{{B_{2} }} \overline{{e_{32} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{10} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{1} }} \overline{{e_{31} }} + \overline{{B_{1} }} \overline{{e_{32} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{1} }} \overline{{e_{31} }} + \overline{{B_{1} }} \overline{{e_{32} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{11} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left[ {\overline{{A_{5} }} \overline{{e_{31} }} + \overline{{B_{5} }} \overline{{e_{32} }} - \overline{{\eta_{33}^{{}} }} \kappa \sin \left( {\kappa z} \right)} \right]\kappa \sin (\kappa z)} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left[ {\overline{{A_{5} }} \overline{{e_{31} }} + \overline{{B_{5} }} \overline{{e_{32} }} - \overline{{\eta_{33}^{{}} }} \kappa \sin \left( {\kappa z} \right)} \right]\kappa \sin (\beta z)} {\text{d}}z, \\ a_{12} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left[ {\overline{{A_{7} }} \overline{{e_{31} }} + \overline{{B_{7} }} \overline{{e_{32} }} - \overline{{m_{33}^{{}} }} \kappa \sin \left( {\kappa z} \right)} \right]\kappa \sin (\kappa z)} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left[ {\overline{{A_{7} }} \overline{{e_{31} }} + \overline{{B_{7} }} \overline{{e_{32} }} - \overline{{m_{33}^{{}} }} \kappa \sin \left( {\kappa z} \right)} \right]\kappa \sin (\kappa z)} {\text{d}}z, \\ \end{aligned}$$

$$\begin{aligned} a_{13} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{9} }} \overline{{e_{31} }} + \overline{{B_{9} }} \overline{{e_{32} }} + \overline{{p_{3} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{9}^{{}} }} \overline{{e_{31} }} + \overline{{B_{9} }} \overline{{e_{32} }} + \overline{{p_{3} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{14} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{9}^{*} }} \overline{{e_{31} }} + \overline{{B_{9}^{*} }} \overline{{e_{32} }} + \overline{{\chi_{3} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{9}^{*} }} \overline{{e_{31} }} + \overline{{B_{9}^{*} }} \overline{{e_{32} }} + \overline{{\chi_{3} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ \end{aligned}$$

$$\begin{aligned} a_{15} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{6} }} \overline{{e_{31} }} + \overline{{B_{6} }} \overline{{e_{32} }} - \overline{{\eta_{33}^{{}} }} \frac{2}{h}} \right)\kappa \sin (\kappa z)} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{6} }} \overline{{e_{31} }} + \overline{{B_{6} }} \overline{{e_{32} }} - \overline{{\eta_{33}^{{}} }} \frac{2}{h}} \right)} \kappa \sin (\kappa z){\text{d}}z, \\ a_{16} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{8}^{{}} }} \overline{{e_{31} }} + \overline{{B_{8}^{{}} }} \overline{{e_{32} }} - \overline{{m_{33}^{{}} }} \frac{2}{h}} \right)} \kappa \sin (\kappa z){\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{8}^{{}} }} \overline{{e_{31} }} + \overline{{B_{8}^{{}} }} \overline{{e_{32} }} - \overline{{m_{33}^{{}} }} \frac{2}{h}} \right)} \kappa \sin (\kappa z){\text{d}}z, \\ a_{21} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{q_{15} }} \cos (\kappa z)} dz + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{q_{15} }} \cos (\kappa z)} {\text{d}}z, \\ a_{22} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{q_{24} }} \cos (\kappa z)} dz + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{q_{24} }} \cos (\kappa z)} {\text{d}}z, \\ a_{23} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left[ {\overline{{q_{15} }} \cos (\kappa z) + \left( {\overline{{A_{3} }} \overline{{q_{31} }} + \overline{{B_{3} }} \overline{{q_{32} }} + \overline{{q_{31} }} z} \right)\kappa \sin (\kappa z)} \right]} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left[ {\overline{{q_{15} }} \cos (\kappa z) + \left( {\overline{{A_{3} }} \overline{{q_{31} }} + \overline{{B_{3} }} \overline{{q_{32} }} + \overline{{q_{31} }} z} \right)\kappa \sin (\kappa z)} \right]} {\text{d}}z, \\ a_{24} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left[ {\overline{{q_{24} }} \cos (\kappa z) + \left( {\overline{{A_{4} }} \overline{{q_{31} }} + \overline{{B_{4} }} \overline{{q_{32} }} + \overline{{q_{32} }} z} \right)\kappa \sin (\kappa z)} \right]} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left[ {\overline{{q_{24} }} \cos (\kappa z) + \left( {\overline{{A_{4} }} \overline{{q_{31} }} + \overline{{B_{4} }} \overline{{q_{32} }} + \overline{{q_{32} }} z} \right)\kappa \sin (\kappa z)} \right]} {\text{d}}z, \\ a_{25} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{m_{11} }} \cos^{2} \left( {\kappa z} \right)} dz + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{m_{11} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z, \\ \end{aligned}$$

$$\begin{aligned} a_{26} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{m_{22} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{m_{22} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z, \\ a_{27} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{\mu_{11} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{\mu_{11} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z, \\ a_{28} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\overline{{\mu_{22} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\overline{{\mu_{22} }} \cos^{2} \left( {\kappa z} \right)} {\text{d}}z, \\ a_{29} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{2} }} \overline{{q_{31} }} + \overline{{B_{2} }} \overline{{q_{32} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{2} }} \overline{{q_{31} }} + \overline{{B_{2} }} \overline{{q_{32} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{30} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{1} }} \overline{{q_{31} }} + \overline{{B_{1} }} \overline{{q_{32} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{1} }} \overline{{q_{31} }} + \overline{{B_{1} }} \overline{{q_{32} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{31} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left[ {\overline{{A_{5} }} \overline{{q_{31} }} + \overline{{B_{5} }} \overline{{q_{32} }} - \overline{{m_{33} }} \kappa \sin \left( {\kappa z} \right)} \right]\kappa \sin (\kappa z)} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left[ {\overline{{A_{5} }} \overline{{q_{31} }} + \overline{{B_{5} }} \overline{{q_{32} }} - \overline{{m_{33} }} \kappa \sin \left( {\kappa z} \right)} \right]\kappa \sin (\kappa z)} {\text{d}}z, \\ \end{aligned}$$

$$\begin{aligned} a_{32} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left[ {\overline{{A_{7} }} \overline{{q_{31} }} + \overline{{B_{7} }} \overline{{q_{32} }} - \overline{{\mu_{33} }} \kappa \sin \left( {\kappa z} \right)} \right]\kappa \sin (\kappa z)} {\text{d}}z \\ & + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left[ {\overline{{A_{7} }} \overline{{q_{31} }} + \overline{{B_{7} }} \overline{{q_{32} }} - \overline{{\mu_{33} }} \kappa \sin \left( {\kappa z} \right)} \right]\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{33} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{9} }} \overline{{q_{31} }} + \overline{{B_{9} }} \overline{{q_{32} }} + \overline{{\lambda_{3} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z \\ & \quad + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{9} }} \overline{{q_{31} }} + \overline{{B_{9} }} \overline{{q_{32} }} + \overline{{\lambda_{3} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{34} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{9}^{*} }} \overline{{q_{31} }} + \overline{{B_{9}^{*} }} \overline{{q_{32} }} + \overline{{\zeta_{3} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z \\ & + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{9}^{*} }} \overline{{q_{31} }} + \overline{{B_{9}^{*} }} \overline{{q_{32} }} + \overline{{\zeta_{3} }} } \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{35} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{6} }} \overline{{q_{31} }} + \overline{{B_{6} }} \overline{{q_{32} }} - \overline{{m_{33} }} \frac{2}{h}} \right)\kappa \sin (\kappa z)} {\text{d}}z \\ & + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{6} }} \overline{{q_{31} }} + \overline{{B_{6} }} \overline{{q_{32} }} - \overline{{m_{33} }} \frac{2}{h}} \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ a_{36} & = \int\limits_{{ - \frac{{h_{c} }}{2} - h_{f} }}^{{ - \frac{{h_{c} }}{2}}} {\left( {\overline{{A_{8} }} \overline{{q_{31} }} + \overline{{B_{8} }} \overline{{q_{32} }} - \overline{{\mu_{33} }} \frac{2}{h}} \right)\kappa \sin (\kappa z)} {\text{d}}z + \int\limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{f} }} {\left( {\overline{{A_{8} }} \overline{{q_{31} }} + \overline{{B_{8} }} \overline{{q_{32} }} - \overline{{\mu_{33} }} \frac{2}{h}} \right)\kappa \sin (\kappa z)} {\text{d}}z, \\ \end{aligned}$$

Appendix 6

$\begin{aligned} l_{1}^{1} & = l_{1} + c_{1} l_{4} + c_{11} l_{5} , \\ l_{2}^{1} & = l_{2} + c_{2} l_{4} + c_{12} l_{5} , \\ l_{3}^{1} & = l_{3} + c_{3} l_{4} + c_{13} l_{5} , \\ l_{4}^{1} & = l_{0} + \\ & \quad + \left( {c_{7} l_{10} + c_{17} l_{11} } \right)\Delta T + \left( {c_{8} l_{10} + c_{18} l_{11} } \right)\Delta m \\ & \quad + \left( {c_{9} l_{10} + c_{19} l_{11} } \right)\phi_{0} + \left( {c_{10} l_{10} + c_{20} l_{11} } \right)\psi_{0} , \\ l_{5}^{1} & = c_{5} l_{10} + c_{15} l_{11} - \lambda_{m}^{2} , \\ l_{6}^{1} & = c_{6} l_{10} + c_{16} l_{11} - \delta_{n}^{2} , \\ l_{7}^{1} & = l_{7} + c_{1} l_{10} + c_{11} l_{11} , \\ l_{8}^{1} & = l_{8} + c_{2} l_{10} + c_{12} l_{11,} \\ l_{9}^{1} & = l_{9} + c_{3} l_{10} + c_{13} l_{11} , \\ l_{10}^{1} & = l_{12} + c_{4} l_{4} + c_{14} l_{5} , \\ l_{11}^{1} & = l_{13} + c_{4} l_{10} + c_{14} l_{11} , \\ l_{12}^{1} & = c_{5} l_{4} + c_{15} l_{5} , \\ l_{13}^{1} & = l_{14} \frac{1}{{R_{x} }} + c_{6} l_{4} + c_{16} l_{5} , \\ l_{14}^{1} & = \left( {c_{7} l_{4} + c_{17} l_{5} } \right)\Delta T + \left( {c_{8} l_{4} + c_{18} l_{5} } \right)\Delta m \\ & \quad + \left( {c_{9} l_{4} + c_{19} l_{5} } \right)\phi_{0} + \left( {c_{10} l_{4} + c_{20} l_{5} } \right)\psi_{0} , \\ \end{aligned}$

$\begin{aligned} l_{21}^{1} & = l_{21} + c_{1} l_{24} + c_{11} l_{25} , \\ l_{22}^{1} & = l_{22} + c_{2} l_{24} + c_{12} l_{25} , \\ l_{23}^{1} & = l_{23} + c_{3} l_{24} + c_{13} l_{25} , \\ l_{24}^{1} & = l_{27} + c_{4} l_{24} + c_{14} l_{25} , \\ l_{25}^{1} & = c_{5} l_{24} + c_{15} l_{25} , \\ l_{26}^{1} & = c_{6} l_{24} + c_{16} l_{25} , \\ l_{27}^{1} & = \left( {c_{7} l_{24} + c_{17} l_{25} } \right)\Delta T + \left( {c_{8} l_{24} + c_{18} l_{25} } \right)\Delta m \\ & \quad + \left( {c_{9} l_{24} + c_{19} l_{25} } \right)\phi_{0} + \left( {c_{10} l_{24} + c_{20} l_{25} } \right)\psi_{0} , \\ l_{31}^{1} & = l_{31} + c_{1} l_{34} + c_{11} l_{35,} \\ l_{32}^{1} & = l_{32} + c_{2} l_{34} + c_{12} l_{35} , \\ l_{33}^{1} & = l_{33} + c_{3} l_{34} + c_{13} l_{35} , \\ l_{34}^{1} & = l_{37} + c_{4} l_{34} + c_{14} l_{35} , \\ l_{35}^{1} & = c_{5} l_{34} + c_{15} l_{35} , \\ l_{36}^{1} & = c_{6} l_{34} + c_{16} l_{35} , \\ l_{37}^{1} & = \left( {c_{7} l_{34} + c_{17} l_{35} } \right)\Delta T + \left( {c_{8} l_{34} + c_{18} l_{35} } \right)\Delta m \\ & \quad + \left( {c_{9} l_{34} + c_{19} l_{35} } \right)\phi_{0} + \left( {c_{10} l_{34} + c_{20} l_{35} } \right)\psi_{0} , \\ \end{aligned}$

$\begin{aligned} & c_{0} = \overline{{a_{4} }} \overline{{a_{25} }} - \overline{{a_{5} }} \overline{{a_{24} }} , \\ & c_{1} = \frac{{\overline{{a_{5} }} \overline{{a_{21} }} - \overline{{a_{1} }} \overline{{a_{25} }} }}{{c_{0} }},\,c_{2} = \frac{{\overline{{a_{5} }} \overline{{a_{22} }} - \overline{{a_{2} }} \overline{{a_{25} }} }}{{c_{0} }}, \\ & c_{3} = \frac{{\overline{{a_{5} }} \overline{{a_{23} }} - \overline{{a_{3} }} \overline{{a_{25} }} }}{{c_{0} }},\,c_{4} = \frac{{\overline{{a_{5} }} \overline{{a_{26} }} - \overline{{a_{6} }} \overline{{a_{25} }} }}{{c_{0} }}, \\ & c_{5} = \frac{{\overline{{a_{5} }} \overline{{a_{27} }} a_{30} - \overline{{a_{7} }} \overline{{a_{25} }} a_{10} }}{{\overline{{a_{4} }} \overline{{a_{25} }} - \overline{{a_{5} }} \overline{{a_{24} }} }}, \\ & c_{6} = \frac{{\overline{{a_{5} }} \overline{{a_{27} }} a_{29} - \overline{{a_{7} }} \overline{{a_{25} }} a_{9} }}{{\overline{{a_{4} }} \overline{{a_{25} }} - \overline{{a_{5} }} \overline{{a_{24} }} }}, \\ & c_{7} = \frac{{\overline{{a_{5} }} \overline{{a_{28} }} - \overline{{a_{8} }} \overline{{a_{25} }} }}{{c_{0} }},\,c_{8} = \frac{{\overline{{a_{5} }} \overline{{a_{29} }} - \overline{{a_{9} }} \overline{{a_{25} }} }}{{c_{0} }}, \\ & c_{9} = \frac{{\overline{{a_{5} }} \overline{{a_{30} }} - \overline{{a_{10} }} \overline{{a_{25} }} }}{{c_{0} }},\,c_{10} = \frac{{\overline{{a_{5} }} \overline{{a_{31} }} - \overline{{a_{11} }} \overline{{a_{25} }} }}{{c_{0} }}, \\ \end{aligned}$

$\begin{aligned} & c_{11} = \frac{{\overline{{a_{1} }} \overline{{a_{24} }} - \overline{{a_{4} }} \overline{{a_{21} }} }}{{c_{0} }},\,c_{12} = \frac{{\overline{{a_{2} }} \overline{{a_{24} }} - \overline{{a_{4} }} \overline{{a_{22} }} }}{{c_{0} }}, \\ & c_{13} = \frac{{\overline{{a_{3} }} \overline{{a_{24} }} - \overline{{a_{4} }} \overline{{a_{23} }} }}{{c_{0} }},\,c_{14} = \frac{{\overline{{a_{6} }} \overline{{a_{24} }} - \overline{{a_{4} }} \overline{{a_{26} }} }}{{c_{0} }}, \\ & c_{15} = \frac{{\overline{{a_{7} }} \overline{{a_{24} }} a_{10} - \overline{{a_{4} }} \overline{{a_{27} }} a_{30} }}{{\overline{{a_{4} }} \overline{{a_{25} }} - \overline{{a_{5} }} \overline{{a_{24} }} }}, \\ & c_{16} = \frac{{\overline{{a_{7} }} \overline{{a_{24} }} a_{9} - \overline{{a_{4} }} \overline{{a_{27} }} a_{29} }}{{\overline{{a_{4} }} \overline{{a_{25} }} - \overline{{a_{5} }} \overline{{a_{24} }} }}, \\ & c_{17} = \frac{{\overline{{a_{8} }} \overline{{a_{24} }} - \overline{{a_{4} }} \overline{{a_{28} }} }}{{c_{0} }},\,c_{18} = \frac{{\overline{{a_{9} }} \overline{{a_{24} }} - \overline{{a_{4} }} \overline{{a_{29} }} }}{{c_{0} }}, \\ & c_{19} = \frac{{\overline{{a_{10} }} \overline{{a_{24} }} - \overline{{a_{4} }} \overline{{a_{30} }} }}{{c_{0} }},\,c_{20} = \frac{{\overline{{a_{11} }} \overline{{a_{24} }} - \overline{{a_{4} }} \overline{{a_{31} }} }}{{c_{0} }}, \\ \end{aligned}$

Appendix 7

$\begin{aligned} & \overline{{n_{0} }} = n_{1} n_{22} - n_{2} n_{21} ,\,\overline{{n_{1} }} = \frac{{n_{3} n_{22} - n_{2} n_{23} }}{{\overline{{n_{0} }} }} \\ & \overline{{n_{2} }} = \frac{{n_{4} n_{22} - n_{2} n_{24} }}{{\overline{{n_{0} }} }},\,\overline{{n_{3} }} = \frac{{n_{5} n_{22} - n_{2} n_{25} }}{{\overline{{n_{0} }} }} \\ & \overline{{n_{4} }} = \frac{{n_{6} n_{22} - n_{2} n_{26} }}{{\overline{{n_{0} }} }},\,\overline{{n_{5} }} = \frac{{n_{7} n_{22} - n_{2} n_{27} }}{{\overline{{n_{0} }} }} \\ & \overline{{n_{6} }} = \frac{{n_{8} n_{22} - n_{2} n_{28} }}{{\overline{{n_{0} }} }},\,\overline{{n_{7} }} = \frac{{n_{9} n_{22} - n_{2} n_{29} }}{{\overline{{n_{0} }} }} \\ & \overline{{n_{8} }} = \frac{{n_{10} n_{22} - n_{2} n_{30} }}{{\overline{{n_{0} }} }} \\ & n_{1} = 1 - c_{5} m_{4} - c_{15} m_{5} ,\,\, \\ & n_{2} = - \left( {c_{6} m_{4} + c_{16} m_{5} } \right), \\ & n_{3} = m_{1} + c_{1} m_{4} + c_{11} m_{5} , \\ & n_{4} = m_{2} + c_{2} m_{4} + c_{12} m_{5} , \\ & n_{5} = m_{3} + c_{3} m_{4} + c_{13} m_{5} , \\ & n_{6} = m_{6} + c_{4} m_{4} + c_{14} m_{5} , \\ & n_{7} = m_{8} + c_{8} m_{4} + c_{18} m_{5} , \\ & n_{8} = m_{8} + c_{8} m_{4} + c_{18} m_{5} , \\ & n_{9} = m_{9} + c_{9} m_{4} + c_{19} m_{5} , \\ & n_{10} = m_{10} + c_{10} m_{4} + c_{20} m_{5} , \\ \end{aligned}$

$\begin{gathered} \overline{{n_{21} }} = \frac{{n_{1} n_{23} - n_{3} n_{21} }}{{\overline{{n_{0} }} }},\,\,\,\,\,\overline{{n_{22} }} = \frac{{n_{1} n_{24} - n_{4} n_{21} }}{{\overline{{n_{0} }} }} \hfill \\ \overline{{n_{23} }} = \frac{{n_{1} n_{25} - n_{5} n_{21} }}{{\overline{{n_{0} }} }},\,\,\,\,\,\overline{{n_{24} }} = \frac{{n_{1} n_{26} - n_{6} n_{21} }}{{\overline{{n_{0} }} }} \hfill \\ \overline{{n_{25} }} = \frac{{n_{1} n_{27} - n_{7} n_{21} }}{{\overline{{n_{0} }} }},\,\,\,\,\,\overline{{n_{26} }} = \frac{{n_{1} n_{28} - n_{8} n_{21} }}{{\overline{{n_{0} }} }} \hfill \\ \overline{{n_{27} }} = \frac{{n_{1} n_{29} - n_{9} n_{21} }}{{\overline{{n_{0} }} }},\,\,\,\,\,\overline{{n_{28} }} = \frac{{n_{1} n_{30} - n_{10} n_{21} }}{{\overline{{n_{0} }} }} \hfill \\ n_{21} = - \left( {c_{5} m_{24} + c_{15} m_{25} } \right),\, \hfill \\ n_{22} = \left( {1 - c_{6} m_{24} - c_{16} m_{25} } \right) \hfill \\ n_{23} = m_{21} + c_{1} m_{24} + c_{11} m_{25} \hfill \\ n_{24} = m_{22} + c_{2} m_{24} + c_{12} m_{25} \hfill \\ n_{25} = m_{23} + c_{3} m_{24} + c_{13} m_{25} \hfill \\ n_{26} = m_{26} + c_{4} m_{24} + c_{14} m_{25} \hfill \\ n_{27} = m_{27} + c_{7} m_{24} + c_{17} m_{25} \hfill \\ n_{28} = m_{28} + c_{8} m_{24} + c_{18} m_{25} \hfill \\ n_{29} = m_{29} + c_{9} m_{24} + c_{19} m_{25} \hfill \\ n_{30} = m_{30} + c_{10} m_{24} + c_{20} m_{25} \hfill \\ \end{gathered}$

$\begin{aligned} & m_{0} = \overline{{A_{1} }} \overline{{B_{2} }} - \overline{{A_{2} }} \overline{{B_{1} }} , \\ & m_{1} = \frac{4}{{mn\pi^{2} }}\left( {\delta_{n}^{2} \overline{{I_{1} }} - \frac{{\overline{{B_{2} }} }}{{R_{x} m_{0} }}} \right), \\ & m_{2} = \frac{4}{{mn\pi^{2} }}\left[ {\delta_{n}^{2} \overline{{I_{2} }} + \frac{{\overline{{A_{3} }} \overline{{B_{2} }} - \overline{{A_{2} }} \overline{{B_{3} }} }}{{m_{0} }}\lambda_{m} } \right], \\ & m_{3} = \frac{4}{{mn\pi^{2} }}\left[ {\delta_{n}^{2} \overline{{I_{3} }} + \frac{{\overline{{A_{4} }} \overline{{B_{2} }} - \overline{{A_{2} }} \overline{{B_{4} }} }}{{m_{0} }}\delta_{n} } \right], \\ & m_{4} = \frac{4}{{mn\pi^{2} }}\left[ {\delta_{n}^{2} \overline{{I_{4} }} + \frac{{\overline{{A_{2} }} \overline{{B_{5} }} - \overline{{A_{5} }} \overline{{B_{2} }} }}{{m_{0} }}} \right], \\ & m_{5} = \frac{4}{{mn\pi^{2} }}\left[ {\delta_{n}^{2} \overline{{I_{5} }} + \frac{{\overline{{A_{2} }} \overline{{B_{7} }} - \overline{{A_{7} }} \overline{{B_{2} }} }}{{m_{0} }}} \right], \\ & m_{6} = \frac{1}{8}\frac{{\overline{{B_{2} }} \lambda_{m}^{2} - \overline{{A_{2} }} \delta_{n}^{2} }}{{m_{0} }},m_{7} = \frac{{\overline{{A_{2} }} \overline{{B_{9} }} - \overline{{A_{9} }} \overline{{B_{2} }} }}{{m_{0} }}, \\ & m_{8} = \frac{{\overline{{A_{2} }} \overline{{B_{9}^{*} }} - \overline{{A_{9}^{*} }} \overline{{B_{2} }} }}{{m_{0} }},m_{9} = \frac{{\overline{{A_{2} }} \overline{{B_{6} }} - \overline{{A_{6} }} \overline{{B_{2} }} }}{{m_{0} }}, \\ & m_{10} = \frac{{\overline{{A_{2} }} \overline{{B_{8} }} - \overline{{A_{8} }} \overline{{B_{2} }} }}{{m_{0} }}, \\ \end{aligned}$

$\begin{aligned} & m_{21} = \frac{4}{{mn\pi^{2} }}\left( {\lambda_{m}^{2} \overline{{I_{1} }} + \frac{{\overline{{B_{1} }} }}{{R_{x} m_{0} }}} \right), \\ & m_{22} = \frac{4}{{mn\pi^{2} }}\left[ {\lambda_{m}^{2} \overline{{I_{2} }} + \frac{{\overline{{A_{1} }} \overline{{B_{3} }} - \overline{{A_{3} }} \overline{{B_{1} }} }}{{m_{0} }}\lambda_{m} } \right], \\ & m_{23} = \frac{4}{{mn\pi^{2} }}\left[ {\lambda_{m}^{2} \overline{{I_{3} }} + \frac{{\overline{{A_{1} }} \overline{{B_{4} }} - \overline{{A_{4} }} \overline{{B_{1} }} }}{{m_{0} }}\delta_{n} } \right], \\ & m_{24} = \frac{4}{{mn\pi^{2} }}\left[ {\lambda_{m}^{2} \overline{{I_{4} }} + \frac{{\overline{{A_{5} }} \overline{{B_{1} }} - \overline{{A_{1} }} \overline{{B_{5} }} }}{{m_{0} }}} \right], \\ & m_{25} = \frac{4}{{mn\pi^{2} }}\left[ {\lambda_{m}^{2} \overline{{I_{5} }} + \frac{{\overline{{A_{7} }} \overline{{B_{1} }} - \overline{{A_{1} }} \overline{{B_{7} }} }}{{m_{0} }}} \right], \\ & m_{26} = \frac{1}{8}\frac{{\overline{{A_{1} }} \delta_{n}^{2} - \overline{{B_{1} }} \lambda_{m}^{2} }}{{m_{0} }},m_{27} = \frac{{\overline{{A_{9} }} \overline{{B_{1} }} - \overline{{A_{1} }} \overline{{B_{9} }} }}{{m_{0} }}, \\ & m_{28} = \frac{{\overline{{A_{9}^{*} }} \overline{{B_{1} }} - \overline{{A_{1} }} \overline{{B_{9}^{*} }} }}{{m_{0} }},m_{29} = \frac{{\overline{{A_{6} }} \overline{{B_{1} }} - \overline{{A_{1} }} \overline{{B_{6} }} }}{{m_{0} }}, \\ & m_{30} = \frac{{\overline{{A_{8} }} \overline{{B_{1} }} - \overline{{A_{1} }} \overline{{B_{8} }} }}{{m_{0} }}, \\ \end{aligned}$

Appendix 8

$\begin{aligned} & \overline{{p_{0} }} = p_{22} p_{33} - p_{23} p_{32} \\ & \overline{{p_{1} }} = \frac{{p_{23} p_{31} - p_{21} p_{33} }}{{p_{0} }} + \frac{{l_{36} p_{23} - l_{26} p_{33} }}{{p_{0} }}, \\ & \overline{{p_{2} }} = \frac{{p_{23} p_{34} - p_{24} p_{33} }}{{p_{0} }}, \\ & \overline{{p_{3} }} = \frac{{p_{23} p_{35} - p_{25} p_{33} }}{{p_{0} }}, \\ \end{aligned}$

$\begin{aligned} & \overline{{p_{21} }} = \frac{{p_{21} p_{32} - p_{22} p_{31} }}{{p_{0} }} + \frac{{l_{26} p_{32} - l_{36} p_{22} }}{{p_{0} }}, \\ & \overline{{p_{22} }} = \frac{{p_{24} p_{32} - p_{22} p_{34} }}{{p_{0} }}, \\ & \overline{{p_{23} }} = \frac{{p_{25} p_{32} - p_{22} p_{35} }}{{p_{0} }}, \\ \end{aligned}$

$\begin{aligned} p_{1} & = l_{1}^{1} + l_{12}^{1} \overline{{n_{1} }} + l_{13}^{1} \overline{{n_{21} }} \\ p_{2} & = l_{2}^{1} + l_{12}^{1} \overline{{n_{2} }} + l_{13}^{1} \overline{{n_{22} }} \\ p_{3} & = l_{3}^{1} + l_{12}^{1} \overline{{n_{3} }} + l_{13}^{1} \overline{{n_{23} }} \\ p_{4} & = l_{4}^{1} + \left( {l_{5}^{1} \overline{{n_{5} }} + l_{6}^{1} \overline{{n_{25} }} } \right)\Delta T\\ &\quad + \left( {l_{5}^{1} \overline{{n_{6} }} + l_{6}^{1} \overline{{n_{26} }} } \right)\Delta m \\ & \quad + \left( {l_{5}^{1} \overline{{n_{7} }} + l_{6}^{1} \overline{{n_{27} }} } \right)\phi_{0}\\ &\quad + \left( {l_{5}^{1} \overline{{n_{8} }} + l_{6}^{1} \overline{{n_{28} }} } \right)\psi_{0} \\ p_{5} & = l_{7}^{1} + l_{5}^{1} \overline{{n_{1} }} + l_{6}^{1} \overline{{n_{21} }} \\ p_{6} & = l_{8}^{1} + l_{5}^{1} \overline{{n_{2} }} + l_{6}^{1} \overline{{n_{22} }} \\ p_{7} & = l_{9}^{1} + l_{5}^{1} \overline{{n_{3} }} + l_{6}^{1} \overline{{n_{23} }} \\ p_{8} & = l_{10}^{1} + l_{12}^{1} \overline{{n_{4} }} + l_{13}^{1} \overline{{n_{24} }} \\ p_{9} & = l_{11}^{1} + l_{5}^{1} \overline{{n_{4} }} + l_{6}^{1} \overline{{n_{24} }} \\ p_{10} & = \left( {l_{12}^{1} \overline{{n_{5} }} + l_{13}^{1} \overline{{n_{25} }} } \right)\Delta T\\ &\quad + \left( {l_{12}^{1} \overline{{n_{6} }} + l_{13}^{1} \overline{{n_{26} }} } \right)\Delta m \\ & \quad + \left( {l_{12}^{1} \overline{{n_{7} }} + l_{13}^{1} \overline{{n_{27} }} } \right)\phi_{0}\\ &\quad + \left( {l_{12}^{1} \overline{{n_{8} }} + l_{13}^{1} \overline{{n_{28} }} } \right)\psi_{0} + l_{14}^{1} \\ \end{aligned}$

$\begin{gathered} p_{21} = l_{21}^{1} + l_{25}^{1} \overline{{n_{1} }} + l_{26}^{1} \overline{{n_{21} }} \hfill \\ p_{22} = l_{22}^{1} + l_{25}^{1} \overline{{n_{2} }} + l_{26}^{1} \overline{{n_{22} }} \hfill \\ p_{23} = l_{23}^{1} + l_{25}^{1} \overline{{n_{3} }} + l_{26}^{1} \overline{{n_{23} }} \hfill \\ p_{24} = l_{24}^{1} + l_{25}^{1} \overline{{n_{4} }} + l_{26}^{1} \overline{{n_{24} }} \hfill \\ p_{25} = \left( {l_{25}^{1} \overline{{n_{5} }} + l_{26}^{1} \overline{{n_{25} }} } \right)\Delta T\\ + \left( {l_{25}^{1} \overline{{n_{6} }} + l_{26}^{1} \overline{{n_{26} }} } \right)\Delta m \hfill \\ + \left( {l_{25}^{1} \overline{{n_{7} }} + l_{26}^{1} \overline{{n_{27} }} } \right)\phi_{0}\\ + \left( {l_{25}^{1} \overline{{n_{8} }} + l_{26}^{1} \overline{{n_{28} }} } \right)\psi_{0} \\ + l_{27}^{1} \hfill \\ \end{gathered}$ $\begin{aligned} p_{31} & = l_{31}^{1} + l_{35}^{1} \overline{{n_{1} }} + l_{36}^{1} \overline{{n_{21} }} \\ p_{32} & = l_{32}^{1} + l_{35}^{1} \overline{{n_{2} }} + l_{36}^{1} \overline{{n_{22} }} \\ p_{33} & = l_{33}^{1} + l_{35}^{1} \overline{{n_{3} }} + l_{36}^{1} \overline{{n_{23} }} \\ p_{34} & = l_{34}^{1} + l_{35}^{1} \overline{{n_{4} }} + l_{36}^{1} \overline{{n_{24} }} \\ p_{35} & = \left( {l_{35}^{1} \overline{{n_{5} }} + l_{36}^{1} \overline{{n_{25} }} } \right)\Delta T\\ &\quad + \left( {l_{35}^{1} \overline{{n_{6} }} + l_{36}^{1} \overline{{n_{26} }} } \right)\Delta m \\ & \quad + \left( {l_{35}^{1} \overline{{n_{7} }} + l_{36}^{1} \overline{{n_{27} }} } \right)\phi_{0}\\ &\quad + \left( {l_{35}^{1} \overline{{n_{8} }} + l_{36}^{1} \overline{{n_{28} }} } \right)\psi_{0} + l_{37}^{1} \\ \end{aligned}$