Skip to main content
SpringerLink
Log in

Large deflection analysis of functionally graded magneto-electro-elastic porous flat panels

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

In this article, an attempt has been made on evaluating the large/nonlinear deflection of functionally graded magneto-electro-elastic porous (FG-MEEP) flat panels taking geometric skewness into consideration. Further, the flat panel is subjected to combined loads which include mechanical, electrical and magnetic loads. The mathematical formulation is derived through higher order shear deformation theory and von-Karman's geometric nonlinearity under the framework of finite element method (FEM). The effective material properties of FG-MEEP material are determined using modified power law. Two forms of material gradation such as ‘B’ rich bottom and ‘F’ rich bottom are modelled and implemented in the analysis. The numerical assessment is carried out to investigate the effect of prominent parameters such as skew angle, porosity distribution, gradient index, porosity volume, functionally graded pattern, electromagnetic loads on the nonlinear deflection of FG-MEEP flat panels. In addition, this study also makes an attempt to evaluate the degree of coupling associated with these parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data availability

The raw/processed data required to reproduce these findings cannot be shared at this time as the data also form part of an ongoing study.

Abbreviations

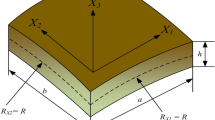
a, b, h :

Length, width and thickness of FG-MEEP flat panel

[\(\overline{C}^{{\rm fg}}\)(z)]:

Elastic stiffness coefficients of FG-MEEP composite

[\(\overline{e}^{{\rm fg}}\)(z)]:

Piezoelectric coefficients of FG-MEEP composite

[\(q^{{\rm fg}}\)(z)]:

Magnetostrictive coefficients of effective FG-MEEP composite

[\(\overline{m}^{{\rm fg}}\)(z)]:

Electromagnetic coefficients of effective FG-MEEP composite

[\(\overline{\eta }^{{\rm fg}}\)(z)]:

Dielectric coefficients of effective FG-MEEP composite

[\(\overline{\mu }^{{\rm fg}}\)(z)]:

Magnetic permeability coefficients of effective FG-MEEP composite

\(\left\{ {\varepsilon^{fg} } \right\}\) :

Strain tensor

\(\left\{ E \right\}\) :

Electric field vector

\(\left\{ H \right\}\) :

Magnetic field vector

\(\left\{ {\sigma^{{\rm fg}} \left( z \right)} \right\}\) :

Stress tensor

\(\left\{ {D^{{\rm fg}} \left( z \right)} \right\}\) :

Electric displacement vector

\(\left\{ {B^{{\rm fg}} \left( z \right)} \right\}\) :

Magnetic flux vector

u 0, v 0, and w 0 :

Midplane displacement along x-, y- and z-axes

\(\theta_{x} , \theta_{y}\) :

Normal transverse rotation about x- and y-axes

\(\left\{ {d_{{\rm t}} } \right\}\) :

Translational displacement

\(\left\{ {d_{{\rm r}} } \right\}\) :

Rotational displacement

\(\left\{ {d_{{\rm r}*} } \right\}\) :

Higher-order rotational displacement

\(\psi\) :

Magnetic potential

\(\phi\) :

Electric potential

λ :

Skew angle of the flat panel

References

  1. Chen D, Yang J, Kitipornchai S (2016) Free and forced vibrations of shear deformable functionally graded porous beams. Int J Mech Sci 108:14–22

    Google Scholar 

  2. Chen D, Kitipornchai S, Yang J (2016) Nonlinear free vibration of shear deformable sandwich beam with a functionally graded porous core. Thin Walled Struct 107:39–48

    Google Scholar 

  3. Chen D, Yang J, Kitipornchai S (2017) Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos Sci Technol 142:235–245

    Google Scholar 

  4. Jabbari M, Mojahedin A, Haghi M (2014) Buckling analysis of thin circular FG plates made of saturated porous-soft ferromagnetic materials in transverse magnetic field. Thin Walled Struct 85:50–56

    Google Scholar 

  5. Jabbari M, Mojahedin A, Joubaneh EF (2015) Thermal buckling analysis of circular plates made of piezoelectric and saturated porous functionally graded material layers. J Eng Mech 141(4):04014148

    Google Scholar 

  6. Rezaei AS, Saidi AR, Abrishamdari M, Mohammadi MP (2017) Natural frequencies of functionally graded plates with porosities via a simple four variable plate theory: an analytical approach. Thin Walled Struct 120:366–377

    Google Scholar 

  7. Ebrahimi F, Jafari A (2018) A four-variable refined shear-deformation beam theory for thermo-mechanical vibration analysis of temperature-dependent FGM beams with porosities. Mech Adv Mater Struct 25(3):212–224

    Google Scholar 

  8. Mojahedin A, Jabbari M, Khorshidvand AR, Eslami MR (2016) Buckling analysis of functionally graded circular plates made of saturated porous materials based on higher order shear deformation theory. Thin Walled Struct 99:83–90

    Google Scholar 

  9. Wattanasakulpong N, Ungbhakorn V (2014) Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerosp Sci Technol 32(1):111–120

    Google Scholar 

  10. Ebrahimi F, Mokhtari M (2015) Transverse vibration analysis of rotating porous beam with functionally graded microstructure using the differential transform method. J Braz Soc Mech Sci Eng 15(4):1435–1444

    Google Scholar 

  11. Ebrahimi F, Zia M (2015) Large amplitude nonlinear vibration analysis of functionally graded Timoshenko beams with porosities. Acta Astronaut 116:117–125

    Google Scholar 

  12. Shafiei N, Mousavi A, Ghadiri M (2016) On size-dependent nonlinear vibration of porous and imperfect functionally graded tapered microbeams. Int J Eng Sci 106:42–56

    MATH  Google Scholar 

  13. Ebrahimi F, Ghasemi F, Salari E (2016) Investigating thermal effects on vibration behavior of temperature-dependent compositionally graded Euler beams with porosities. Meccanica 51(1):223–249

    MathSciNet  MATH  Google Scholar 

  14. Barati MR, Zenkour AM (2018) Electro-thermoelastic vibration of plates made of porous functionally graded piezoelectric materials under various boundary conditions. J Vib Control 24(10):1910–1926

    MathSciNet  Google Scholar 

  15. Ebrahimi F, Habibi S (2016) Deflection and vibration analysis of higher-order shear deformable compositionally graded porous plate. Steel Compos Struct 20(1):205–225

    Google Scholar 

  16. Vinyas M (2020) Interphase effect on the controlled frequency response of three-phase smart magneto-electro-elastic plates embedded with active constrained layer damping: FE study. Mater Res Express 6:125707

    Google Scholar 

  17. Vinyas M (2019) Vibration control of skew magneto-electro-elastic plates using active constrained layer damping. Compos Struct 208:600–617

    Google Scholar 

  18. Ebrahimi F, Barati MR, Tornabene F (2019) Mechanics of nonlocal advanced magneto-electro-viscoelastic plates. Struct Eng Mech 71(3):257–269

    Google Scholar 

  19. Shariati A, Barati MR, Ebrahimi F, Singhal A, Toghroli A (2020) Investigating vibrational behavior of graphene sheets under linearly varying in-plane bending load based on the nonlocal strain gradient theory. Adv Nano Res 8(4):265–276

    Google Scholar 

  20. Barati MR, Shahverdi H (2020) Finite element forced vibration analysis of refined shear deformable nanocomposite graphene platelet-reinforced beams. J Braz Soc Mech Sci Eng 42(1):33

    Google Scholar 

  21. Ebrahimi F, Barati MR (2019) Hygrothermal effects on static stability of embedded single-layer graphene sheets based on nonlocal strain gradient elasticity theory. J Therm Stress 42(12):1535–1550

    Google Scholar 

  22. Ebrahimi F, Barati MR (2019) Buckling characteristics of bilayer graphene sheets subjected to humid thermomechanical loading. In: Handbook of graphene, volume 8: technology and innovations, p 433. https://doi.org/10.1002/9781119468455.ch138

  23. Vinyas M, Kattimani SC (2018) Investigation of the effect of BaTiO3/CoFe2O4 particle arrangement on the static response of magneto-electro-thermo-elastic plates. Compos Struct 185:51–64

    Google Scholar 

  24. Vinyas M, Kattimani SC, Loja MAR, Vishwas M (2018) Effect of BaTiO3/CoFe2O4 micro-topological textures on the coupled static behaviour of magneto-electro-thermo-elastic beams in different thermal environment. Mater Res Express 5:125702

    Google Scholar 

  25. Huang DJ, Ding HJ, Chen WQ (2007) Analytical solution for functionally graded magneto-electro-elastic plane beams. Int J Eng Sci 45(2–8):467–485

    Google Scholar 

  26. Milazzo A (2014) Refined equivalent single layer formulations and finite elements for smart laminates free vibrations. Compos Part B Eng 61:238–253

    Google Scholar 

  27. Vinyas M, Harursampath D, Trung NT (2019) Influence of active constrained layer damping on the coupled vibration response of functionally graded magneto-electro-elastic plates with skewed edges. Def Technol. https://doi.org/10.1016/j.dt.2019.11.016

    Article  Google Scholar 

  28. Pan E, Han F (2005) Exact solution for functionally graded and layered magneto-electro-elastic plates. Int J Eng Sci 43(3–4):321–339

    Google Scholar 

  29. Ramirez F, Heyliger PR, Pan E (2006) Discrete layer solution to free vibrations of functionally graded magneto-electro-elastic plates. Mech Adv Mater Struct 13(3):249–266

    Google Scholar 

  30. Bhangale RK, Ganesan N (2006) Free vibration of simply supported functionally graded and layered magneto-electro-elastic plates by finite element method. J Sound Vib 294(4):1016–1038

    MATH  Google Scholar 

  31. Feng WJ, Su RKL (2006) Dynamic internal crack problem of a functionally graded magneto-electro-elastic strip. Int J Solids Struct 43(17):5196–5216

    MATH  Google Scholar 

  32. Wu CP, Tsai YH (2010) Dynamic responses of functionally graded magneto-electro-elastic shells with closed-circuit surface conditions using the method of multiple scales. Eur J Mech A Solid 29(2):166–181

    MathSciNet  MATH  Google Scholar 

  33. Bhangale RK, Ganesan N (2005) Free vibration studies of simply supported non-homogeneous functionally graded magneto-electro-elastic finite cylindrical shells. J Sound Vib 288:412–422

    Google Scholar 

  34. Wu CP, Tsai YH (2007) Static behavior of functionally graded magneto-electro-elastic shells under electric displacement and magnetic flux. Int J Eng Sci 45:744–769

    Google Scholar 

  35. Vinyas M, Kattimani SC (2017) Multiphysics response of magneto-electro-elastic beams in thermo-mechanical environment. Coupled Syst Mech 6(3):351–368

    Google Scholar 

  36. Li XY, Ding HJ, Chen WQ (2008) Three-dimensional analytical solution for functionally graded magneto-electro-elastic circular plates subjected to uniform load. Compos Struct 83:381–390

    Google Scholar 

  37. Sladek J, Sladek V, Krahulec S, Chen CS, Young DL (2015) Analyses of circular magnetoelectroelastic plates with functionally graded material properties. Mech Adv Mater Struct 22:479–489

    Google Scholar 

  38. Vinyas M, Kattimani SC (2017) Static studies of stepped functionally graded magneto-electro-elastic beam subjected to different thermal loads. Compos Struct 163:216–237

    Google Scholar 

  39. Vinyas M, Kattimani SC (2017) Static analysis of stepped functionally graded magneto-electro-elastic plates in thermal environment: a finite element study. Compos Struct 178:63–85

    Google Scholar 

  40. Vinyas M, Piyush JS, Kattimani SC (2017) Influence of coupled fields on free vibration and static behaviour of functionally graded magneto-electro-thermo-elastic plate. J Intell Mater Syst Struct 29(7):1430–1455

    Google Scholar 

  41. Vinyas M (2020) Computational analysis of smart magneto-electro-elastic materials and structures: review and classification. Arch Comput Methods Eng. https://doi.org/10.1007/s11831-020-09406-4

    Article  MathSciNet  Google Scholar 

  42. Ebrahimi F, Shafiei N (2017) Influence of initial shear stress on the vibration behavior of single-layered graphene sheets embedded in an elastic medium based on Reddy’s higher-order shear deformation plate theory. Mech Adv Mater Struct 24(9):761–772

    Google Scholar 

  43. Ebrahimi F, Barati MR (2016) Electromechanical buckling behavior of smart piezoelectrically actuated higher-order size-dependent graded nanoscale beams in thermal environment. Int J Smart Nano Mater 7(2):69–90

    Google Scholar 

  44. Ebrahimi F, Farazmandnia N (2017) Thermo-mechanical vibration analysis of sandwich beams with functionally graded carbon nanotube-reinforced composite face sheets based on a higher-order shear deformation beam theory. Mech Adv Mater Struct 24(10):820–829

    Google Scholar 

  45. Ebrahimi F, Barati MR (2016) A nonlocal higher-order shear deformation beam theory for vibration analysis of size-dependent functionally graded nanobeams. Arab J Sci Eng 41(5):1679–1690

    MathSciNet  MATH  Google Scholar 

  46. Ebrahimi F, Barati MR (2017) Buckling analysis of nonlocal third-order shear deformable functionally graded piezoelectric nanobeams embedded in elastic medium. J Braz Soc Mech Sci Eng 39(3):937–952

    Google Scholar 

  47. Moita JMS, Soares CMM, Soares CAM (2009) Analyses of magneto-electro-elastic plates using a higher order finite element model. Compos Struct 91(4):421–426

    Google Scholar 

  48. Lage RG, Soares CMM, Soares CAM, Reddy JN (2004) Layerwise partial mixed finite element analysis of magneto-electro-elastic plates. Comput Struct 82(17):1293–1301

    Google Scholar 

  49. Shooshtari A, Razavi S (2016) Vibration analysis of a magnetoelectroelastic rectangular plate based on a higher-order shear deformation theory. Lat Am J Solids Struct 13(3):554–572

    Google Scholar 

  50. Vinyas M, Kattimani SC (2018) Finite element evaluation of free vibration characteristics of magneto-electro-elastic plates in hygrothermal environment using higher order shear deformation theory. Compos Struct 202:1339–1352

    Google Scholar 

  51. Vinyas M, Kattimani SC, Harursampath D, Trung NT (2019) Coupled evaluation of the free vibration characteristics of magneto-electro-elastic skew plates in hygrothermal environment. Smart Struct Syst 24(2):267–292

    Google Scholar 

  52. Vinyas M, Nischith G, Loja MAR, Ebrahimi F, Duc ND (2019) Numerical analysis of the vibration response of skew magneto-electro-elastic plates based on the higher-order shear deformation theory. Compos Struct 214:132–142

    Google Scholar 

  53. Vinyas M (2019) A higher order free vibration analysis of carbon nanotube-reinforced magneto-electro-elastic plates using finite element methods. Compos Part B: Eng 158:286–301

    Google Scholar 

  54. Vinyas M, Harursampath D, Trung N-T (2020) A higher order coupled frequency characteristics study of smart magneto-electro-elastic composite plates with cut-outs using finite element method. Def Technol. https://doi.org/10.1016/j.dt.2020.02.009

    Article  Google Scholar 

  55. Vinyas M, Sunny KK, Harursampath D, Trung NT, Loja MAR (2019) Influence of interphase on the multi-physics coupled frequency of three phase smart magneto-electro-elastic composite plates. Compos Struct 226:111254

    Google Scholar 

  56. Vinyas M, Sandeep AS, Trung NT, Ebrahimi F, Duc ND (2019) A finite element based assessment of free vibration behaviour of circular and annular magneto-electro-elastic plates using higher order shear deformation theory. J Intell Mater Syst Struct 30(6):2478–2501

    Google Scholar 

  57. Vinyas M (2020) On frequency response of porous functionally graded magneto-electro-elastic circular and annular plates with different electro-magnetic conditions using HSDT. Compos Struct 240:112044

    Google Scholar 

  58. Vinyas M, Harursampath D, Kattimani SC (2020) On vibration analysis of functionally graded carbon nanotube reinforced magneto-electro-elastic plates with different electro-magnetic conditions using higher order finite element methods. Def Technol. https://doi.org/10.1016/j.dt.2020.03.012

    Article  Google Scholar 

  59. Vinyas M, Harursampath D, Kattimani SC (2020) Thermal response analysis of multi-layered magneto-electro-thermo-elastic plates using Reddy’s third order shear deformation theory. Struct Eng Mech 73(6):667–684

    Google Scholar 

  60. Shooshtari A, Razavi S (2016) Large amplitude free vibration of magneto-electro-elastic curved panels. Sci Iran 23(6):2606–2615

    Google Scholar 

  61. Sladek J, Sladek V, Krahulec S, Pan E (2013) The MLPG analyses of large deflections of magnetoelectroelastic plates. Eng Anal Bound Elem 37(4):673–682

    MathSciNet  MATH  Google Scholar 

  62. Milazzo A (2014) Large deflection of magneto-electro-elastic laminated plates. Appl Math Model 38(5–6):1737–1752

    MathSciNet  MATH  Google Scholar 

  63. Shabanpour S, Razavi S, Shooshtari A (2019) Nonlinear vibration analysis of laminated magneto-electro-elastic rectangular plate based on third-order shear deformation theory. Iran J Sci Technol Trans Mech Eng 43(1):211–223

    Google Scholar 

  64. Vinyas M, Harursampath D (2020) Nonlinear vibrations of magneto-electro-elastic doubly curved shells reinforced with carbon nanotubes. Compos Struct 253:112749

    Google Scholar 

  65. Mahesh V, Harursampath D (2020) Nonlinear vibration of functionally graded magneto-electro-elastic higher order plates reinforced by CNTs using FEM. Eng Comput. https://doi.org/10.1007/s00366-020-01098-5

    Article  Google Scholar 

  66. Mahesh V, Harursampath D (2020) Nonlinear deflection analysis of CNT/magneto-electro-elastic smart shells under multiphysics loading. Mech Adv Mater Struct. https://doi.org/10.1080/15376494.2020.1805059

    Article  Google Scholar 

  67. Mahesh V (2020) Nonlinear deflection of carbon nanotube reinforced multiphase magneto-electro-elastic plates in thermal environment considering pyrocoupling effects. Math Methods Appl Sci. https://doi.org/10.1002/mma.6858

    Article  Google Scholar 

  68. Reddy JN (2004) An introduction to nonlinear finite element analysis. Oxford University Press, Cambridge

    MATH  Google Scholar 

Download references

Acknowledgements

The author acknowledges the support of Indian Institute of Science, Bangalore, through C.V. Raman Post-doctoral fellowship R(IA)/CVR-PDF/2019/1630, under Institution of Eminence scheme.

Author information

Authors and Affiliations

  1. Nonlinear Multifunctional Composites Analysis and Design (NMCAD) Laboratory, Department of Aerospace Engineering, Indian Institute of Science, Bangalore, 560012, India

    Vinyas Mahesh & Dineshkumar Harursampath

  2. Composite Research: Experimentation, Analysis and Modelling (CREAM) Lab, Department of Mechanical Engineering, Nitte Meenakshi Institute of Technology, Bangalore, 560064, India

    Vinyas Mahesh

Authors
  1. Vinyas Mahesh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dineshkumar Harursampath
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vinyas Mahesh.

Ethics declarations

Conflict of interest

The authors declare that they have no competing interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The equivalent stiffness matrix and force vector appearing in Eq. (18) can be explicitly shown as follows:

$$\begin{aligned} & \left[ {K_{{{\text{eq}}}}^{{\text{e}}} } \right] = \left[ {K_{55}^{{\text{e}}} } \right] - \left[ {K_{56}^{{\text{e}}} } \right]\left[ {K_{47}^{{\text{e}}} } \right] \\ & \left\{ {F_{{{\text{eq}}}} } \right\} = \left[ {K_{56} } \right]\left[ {K_{46} } \right]^{ - 1} \left\{ {F{}_{4}} \right\} - \left\{ {F_{7} } \right\}. \\ \end{aligned}$$
(22)

The constituent stiffness matrices of Eq. (22) can be given as follows:

$$\begin{aligned} & \left[ {K_{1}^{{\text{e}}} } \right] = \left[ {K_{{{\text{tbNLbNL}}1\_{\text{tbtbNL}}1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{ts}}1}}^{{\text{e}}} } \right];\quad \left[ {K_{2}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rbNL}}\_{\text{rtb}}24}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{rts}}13}}^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{3}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rbNL}}\_{\text{rtb}}4}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{rts}}3}}^{{\text{e}}} } \right]^{{\text{T}}} ;\quad \left[ {K_{4}^{{\text{e}}} } \right] = \left[ {K_{{{\text{bNL}}\_{\text{tb}}\phi 1}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{ts}}\phi 1}}^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{5}^{{\text{e}}} } \right] = \left[ {K_{{{\text{bNL}}\_{\text{tb}}\psi 1}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{ts}}\psi 1}}^{{\text{e}}} } \right]^{T} ;\quad \left[ {K_{6}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rtbrbNL}}24}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rts}}13}}^{{\text{e}}} } \right] \\ & \left[ {K_{7}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrb}}3557}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrs}}3513}}^{{\text{e}}} } \right];\quad \left[ {K_{8}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrb}}57}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrs}}35}}^{{\text{e}}} } \right] \\ & \left[ {K_{9}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\phi 24}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\phi {\text{s}}13}}^{{\text{e}}} } \right]^{{\text{T}}} ;\quad \left[ {K_{10}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\psi 24}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\psi {\text{s}}13}}^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{11}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rtbrbNL}}4}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rts}}3}}^{{\text{e}}} } \right];\quad \left[ {K_{12}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrb}}57}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrs}}35}}^{{\text{e}}} } \right] \\ & \left[ {K_{13}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrb}}7}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrs}}5}}^{{\text{e}}} } \right];\quad \left[ {K_{14}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\phi 4}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\phi {\text{s}}3}}^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{15}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\psi 4}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\psi {\text{s}}3}}^{{\text{e}}} } \right]^{{\text{T}}} ;\quad \left[ {K_{16}^{{\text{e}}} } \right] = \left[ {K_{{{\text{tb}}\phi 1}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{bNL}}\phi 1}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{ts}}\phi 1}}^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{17}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\phi 2}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{rb}}\phi 4}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\phi {\text{s}}1}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\phi {\text{s}}3}}^{{\text{e}}} } \right]^{{\text{T}}} ; \\ & \left[ {K_{18}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\phi 4}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\phi {\text{s}}3}}^{{\text{e}}} } \right]^{{\text{T}}} ;\quad \left[ {K_{19}^{{\text{e}}} } \right] = \left[ {K_{{{\text{tb}}\psi 1}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{bN}}\psi 1}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{ts}}\psi 1}}^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{20}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\psi 2}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{rb}}\psi 4}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\psi {\text{s}}1}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\psi {\text{s}}3}}^{{\text{e}}} } \right]^{{\text{T}}} ; \\ \end{aligned}$$
$$\begin{aligned} & \left[ {K_{21}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\psi 4}}^{{\text{e}}} } \right]^{{\text{T}}} + \left[ {K_{{{\text{r}}\psi {\text{s}}3}}^{{\text{e}}} } \right]^{{\text{T}}} ,\quad \left[ {K_{22}^{{\text{e}}} } \right] = \left[ {K_{16}^{{\text{e}}} } \right] - \left[ {K_{\phi \psi }^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{19}^{{\text{e}}} } \right] \\ & \left[ {K_{23}^{{\text{e}}} } \right] = \left[ {K_{17}^{{\text{e}}} } \right] - \left[ {K_{\phi \psi }^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{20}^{{\text{e}}} } \right],\quad \left[ {K_{24}^{{\text{e}}} } \right] = \left[ {K_{18}^{{\text{e}}} } \right] - \left[ {K_{\phi \psi }^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{21}^{{\text{e}}} } \right], \\ & \left[ {K_{25}^{{\text{e}}} } \right] = \left[ {K_{\phi \phi }^{{\text{e}}} } \right] - \left[ {K_{\phi \psi }^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{\phi \psi }^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{26}^{{\text{e}}} } \right] = \left[ {K_{25}^{{\text{e}}} } \right]^{ - 1} \left[ {K_{22}^{{\text{e}}} } \right]^{{\text{T}}} ;\quad \left[ {K_{27}^{{\text{e}}} } \right] = \left[ {K_{25}^{{\text{e}}} } \right]^{ - 1} \left[ {K_{23}^{{\text{e}}} } \right]^{{\text{T}}} ;\quad \left[ {K_{28}^{{\text{e}}} } \right] = \left[ {K_{25}^{{\text{e}}} } \right]^{ - 1} \left[ {K_{24}^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{29}^{{\text{e}}} } \right] = \left[ {K_{11}^{{\text{e}}} } \right] - \left[ {K_{15}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{19}^{{\text{e}}} } \right];\quad \left[ {K_{30}^{{\text{e}}} } \right] = \left[ {K_{12}^{{\text{e}}} } \right] - \left[ {K_{15}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{20}^{{\text{e}}} } \right] \\ & \left[ {K_{31}^{{\text{e}}} } \right] = \left[ {K_{13}^{{\text{e}}} } \right] - \left[ {K_{15}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{21}^{{\text{e}}} } \right];\left[ {K_{32}^{{\text{e}}} } \right] = \left[ {K_{14}^{{\text{e}}} } \right] - \left[ {K_{15}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{\phi \psi }^{{\text{e}}} } \right]^{{\text{T}}} \\ & \left[ {K_{33}^{{\text{e}}} } \right] = \left[ {K_{29}^{{\text{e}}} } \right] - \left[ {K_{32}^{{\text{e}}} } \right]\left[ {K_{26}^{{\text{e}}} } \right],\quad \left[ {K_{34}^{{\text{e}}} } \right] = \left[ {K_{30}^{{\text{e}}} } \right] - \left[ {K_{32}^{{\text{e}}} } \right]\left[ {K_{27}^{{\text{e}}} } \right] \\ & \left[ {K_{35}^{{\text{e}}} } \right] = \left[ {K_{31}^{{\text{e}}} } \right] - \left[ {K_{32}^{{\text{e}}} } \right]\left[ {K_{28}^{{\text{e}}} } \right],\quad \left[ {K_{36}^{{\text{e}}} } \right] = \left[ {K_{35}^{{\text{e}}} } \right]^{ - 1} \left[ {K_{33}^{{\text{e}}} } \right]^{{\text{T}}} ; \\ & \left[ {K_{37}^{{\text{e}}} } \right] = \left[ {K_{35}^{{\text{e}}} } \right]^{ - 1} \left[ {K_{34}^{{\text{e}}} } \right]^{T} \left[ {K_{38}^{{\text{e}}} } \right] = \left[ {K_{6}^{{\text{e}}} } \right] - \left[ {K_{10}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{19}^{{\text{e}}} } \right]; \\ & \left[ {K_{39}^{{\text{e}}} } \right] = \left[ {K_{7}^{{\text{e}}} } \right] - \left[ {K_{10}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{20}^{{\text{e}}} } \right];\quad \left[ {K_{40}^{{\text{e}}} } \right] = \left[ {K_{8}^{{\text{e}}} } \right] - \left[ {K_{10}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{21}^{{\text{e}}} } \right]; \\ \end{aligned}$$
$$\begin{aligned} & \left[ {K_{41}^{{\text{e}}} } \right] = \left[ {K_{9}^{{\text{e}}} } \right] - \left[ {K_{10}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{\phi \psi }^{{\text{e}}} } \right]^{{\text{T}}} ;\quad \left[ {K_{42}^{{\text{e}}} } \right] = \left[ {K_{38}^{{\text{e}}} } \right] - \left[ {K_{41}^{{\text{e}}} } \right]\left[ {K_{26}^{{\text{e}}} } \right] \\ & \left[ {K_{43}^{{\text{e}}} } \right] = \left[ {K_{39}^{{\text{e}}} } \right] - \left[ {K_{41}^{{\text{e}}} } \right]\left[ {K_{27}^{{\text{e}}} } \right];\quad \left[ {K_{44}^{{\text{e}}} } \right] = \left[ {K_{40}^{{\text{e}}} } \right] - \left[ {K_{41}^{{\text{e}}} } \right]\left[ {K_{28}^{{\text{e}}} } \right] \\ & \left[ {K_{45}^{{\text{e}}} } \right] = \left[ {K_{42}^{{\text{e}}} } \right] - \left[ {K_{44}^{{\text{e}}} } \right]\left[ {K_{36}^{{\text{e}}} } \right];\quad \left[ {K_{46}^{{\text{e}}} } \right] = \left[ {K_{43}^{{\text{e}}} } \right] - \left[ {K_{44}^{{\text{e}}} } \right]\left[ {K_{37}^{{\text{e}}} } \right] \\ & \left[ {K_{47}^{{\text{e}}} } \right] = \left[ {K_{46}^{{\text{e}}} } \right]^{ - 1} \left[ {K_{45}^{{\text{e}}} } \right];\quad \left[ {K_{48}^{{\text{e}}} } \right] = \left[ {K_{1}^{{\text{e}}} } \right] - \left[ {K_{5}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{19}^{{\text{e}}} } \right] \\ & \left[ {K_{49}^{{\text{e}}} } \right] = \left[ {K_{2}^{{\text{e}}} } \right] - \left[ {K_{5}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{20}^{{\text{e}}} } \right];\quad \left[ {K_{50}^{{\text{e}}} } \right] = \left[ {K_{3}^{{\text{e}}} } \right] - \left[ {K_{5}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{21}^{{\text{e}}} } \right] \\ & \left[ {K_{51}^{{\text{e}}} } \right] = \left[ {K_{4}^{{\text{e}}} } \right] - \left[ {K_{5}^{{\text{e}}} } \right]\left[ {K_{\psi \psi }^{{\text{e}}} } \right]^{ - 1} \left[ {K_{\phi \psi }^{{\text{e}}} } \right]^{{\text{T}}} ;\quad \left[ {K_{52}^{{\text{e}}} } \right] = \left[ {K_{48}^{{\text{e}}} } \right] - \left[ {K_{51}^{{\text{e}}} } \right]\left[ {K_{26}^{{\text{e}}} } \right] \\ & \left[ {K_{53}^{{\text{e}}} } \right] = \left[ {K_{49}^{{\text{e}}} } \right] - \left[ {K_{51}^{{\text{e}}} } \right]\left[ {K_{27}^{{\text{e}}} } \right];\quad \left[ {K_{54}^{{\text{e}}} } \right] = \left[ {K_{50}^{{\text{e}}} } \right] - \left[ {K_{51}^{{\text{e}}} } \right]\left[ {K_{28}^{{\text{e}}} } \right] \\ & \left[ {K_{55}^{{\text{e}}} } \right] = \left[ {K_{52}^{{\text{e}}} } \right] - \left[ {K_{54}^{{\text{e}}} } \right]\left[ {K_{36}^{{\text{e}}} } \right];\quad \left[ {K_{56}^{{\text{e}}} } \right] = \left[ {K_{53}^{{\text{e}}} } \right] - \left[ {K_{54}^{{\text{e}}} } \right]\left[ {K_{37}^{{\text{e}}} } \right] \\ \end{aligned}$$
(23)
$$\begin{aligned} & \left[ {K_{{{\text{rrs}}35}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrs}}3}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrs}}5}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rrs}}13}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrs}}1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrs}}3}}^{{\text{e}}} } \right], \\ & \left[ {K_{{{\text{rrs}}3513}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrs}}35}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrs}}13}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rts}}13}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rts}}1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rts}}3}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{r}}\psi {\text{s}}13}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{r}}\psi {\text{s}}1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{r}}\psi {\text{s}}3}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{r}}\phi {\text{s}}13}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{r}}\phi {\text{s}}1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{r}}\phi {\text{s}}3}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{tbtbNL}}1}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{tb}}1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{tbNL}}1}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rtb}}24}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rtb}}2}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rtb}}4}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{tbNLbNL}}1\_{\text{tbtbNL}}1}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{tbNLbNL}}1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{tbtbNL}}1}}^{{\text{e}}} } \right], \\ & \left[ {K_{{{\text{rbNL}}\_{\text{rtb}}24}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rbNL}}24}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rtb}}24}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rbNL}}\_{\text{rtb}}4}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rbNL}}4}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rtb}}4}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{bNL}}\_{\text{tb}}\phi 1}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{bNL}}\phi 1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{tb}}\phi 1}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{bNL}}\_{\text{tb}}\psi 1}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{bNL}}\psi 1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{tb}}\psi 1}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{rrb}}57}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrb}}5}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrb}}7}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rtbrbNL}}4}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rtb}}4}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rbNL}}4}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{rtbrbNL}}2}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rtb}}2}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rbNL}}2}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rtbrbNL}}24}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rtbrbNL}}2}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rtbrbNL}}4}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{rrb}}35}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrb}}3}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrb}}5}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rrb}}5735}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rrb}}57}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rrb}}35}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{rb}}\phi 24}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\phi 2}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rb}}\phi 4}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rb}}\psi 24}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rb}}\psi 2}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rb}}\psi 4}}^{{\text{e}}} } \right] \\ & \left[ {K_{{{\text{tbNLbNL}}1}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{tbNL}}1}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{bNL}}1}}^{{\text{e}}} } \right],\quad \left[ {K_{{{\text{rbNL}}24}}^{{\text{e}}} } \right] = \left[ {K_{{{\text{rbNL}}2}}^{{\text{e}}} } \right] + \left[ {K_{{{\text{rbNL}}4}}^{{\text{e}}} } \right]. \\ \end{aligned}$$
(24)

The force vectors and stiffness matrices contributing to \(\left\{{F}_{\mathrm{eq}}\right\}\) can be shown as follows:

$$\begin{aligned} & \left\{ {F{}_{1}} \right\} = - \left[ { - \left\{ {F_{\phi } } \right\} + \left[ {K_{\phi \psi } } \right]\left[ {K_{\psi \psi } } \right]^{ - 1} \left\{ {F_{\psi } } \right\}} \right] \\ & \left\{ {F_{2} } \right\} = \left[ {K_{32} } \right]\left[ {K_{25} } \right]^{ - 1} \left\{ {F{}_{1}} \right\} + \left[ {K_{15} } \right]\left[ {K_{\psi \psi } } \right]^{ - 1} \left\{ {F{}_{\psi }} \right\} \\ & \left\{ {F_{3} } \right\} = \left[ {K_{41} } \right]\left[ {K_{25} } \right]^{ - 1} \left\{ {F{}_{1}} \right\} + \left[ {K_{10} } \right]\left[ {K_{\psi \psi } } \right]^{ - 1} \left\{ {F{}_{\psi }} \right\} \\ & \left\{ {F_{4} } \right\} = \left\{ {F_{3} } \right\} - \left[ {K_{44} } \right]\left[ {K_{35} } \right]^{ - 1} \left\{ {F{}_{2}} \right\} \\ & \left\{ {F_{5} } \right\} = \left\{ {F_{m} } \right\} - \left[ {K_{5} } \right]\left[ {K_{\psi \psi } } \right]^{ - 1} \left\{ {F{}_{\psi }} \right\} \\ & \left\{ {F_{6} } \right\} = \left[ {K_{51} } \right]\left[ {K_{25} } \right]^{ - 1} \left\{ {F{}_{1}} \right\} - \left\{ {F_{5} } \right\} \\ & \left\{ {F_{7} } \right\} = \left\{ {F_{6} } \right\} - \left[ {K_{54} } \right]\left[ {K_{35} } \right]^{ - 1} \left\{ {F{}_{2}} \right\}. \\ \end{aligned}$$
(25)

The expressions for stiffness matrices and force vectors are as follows:

$$\begin{aligned} & \left[ {K_{{{\text{rtb}}4}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}4}} } \right]} } \left[ {B_{{{\text{tb}}}} } \right]{\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rbNL}}4}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{bNL}}4}} } \right]} } \left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{rrb}}5}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}5}} } \right]} } \left[ {B_{{{\text{rb}}}} } \right]{\text{d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rrb}}7}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}7}} } \right]} } \left[ {B_{{{\text{rb}}}} } \right]{\text{d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{rb}}\phi 4}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}\phi 4}} } \right]} } \left[ {B_{\phi } } \right]{\text{d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rb}}\psi 4}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}\psi 4}} } \right]} } \left[ {B_{\psi } } \right]\,{\text{d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{rt}}b4}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}4}} } \right]} } \left[ {B_{{{\text{tb}}}} } \right]\,{\text{d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rtb}}2}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}2}} } \right]} } \left[ {B_{{{\text{tb}}}} } \right]\,{\text{d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{rbNL}}2}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{bNL}}2}} } \right]} } \left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rrb}}3}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}3}} } \right]} } \left[ {B_{{{\text{rb}}}} } \right]{\text{ d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{rrb}}5}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}5}} } \right]} } \left[ {B_{{{\text{rb}}}} } \right]{\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rb}}\phi 2}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}\phi 2}} } \right]} } \left[ {B_{\phi } } \right]{\text{d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{rb}}\psi 2}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}\psi 2}} } \right]} } \left[ {B_{\psi } } \right]{\text{d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{tbNL}}1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{tb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{bNL}}1}} } \right]} } \left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{ d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{bNL}}1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{2} } \right]^{{\text{T}}} \left[ {B_{1} } \right]^{{\text{T}}} \left[ {D_{{{\text{bbNL}}1}} } \right]} } \left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{ d}}x\,{\text{d}}y; \\ & \left[ {K_{{{\text{bNL}}\phi 1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{\phi } } \right]^{{\text{T}}} \left[ {D_{{{\text{bNL}}\phi 1}} } \right]} } \left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{bNL}}\psi 1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{\psi } } \right]^{{\text{T}}} \left[ {D_{{{\text{bNL}}\psi 1}} } \right]} } \left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{tb}}1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{tb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}1}} } \right]} } \left[ {B_{{{\text{tb}}}} } \right]{\text{d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{tb}}\phi 1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{tb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}\phi 1}} } \right]} } \left[ {B_{\phi } } \right]{\text{d}}x\,{\text{d}}y \\ \end{aligned}$$
$$\begin{aligned} & \left[ {K_{{{\text{tb}}\psi 1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{tb}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{b}}\psi 1}} } \right]} } \left[ {B_{\psi } } \right]{\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rts}}3}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}3}} } \right]\left[ {B_{{{\text{ts}}}} } \right]} } {\text{ d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{rrs}}3}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}3}} } \right]\left[ {B_{{{\text{rs}}}} } \right]} } {\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rrs}}5}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}5}} } \right]\left[ {B_{{{\text{rs}}}} } \right]} } {\text{ d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{r}}\psi {\text{s}}3}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}\psi 3}} } \right]\left[ {B_{\psi } } \right]} } {\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{r}}\phi {\text{s}}3}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}\phi 3}} } \right]\left[ {B_{\phi } } \right]} } {\text{ d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{ts}}\phi 1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{ts}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}\phi 1}} } \right]} } \left[ {B_{\phi } } \right]{\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{ts}}\psi 1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{ts}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}\psi 1}} } \right]} } \left[ {B_{\psi } } \right]{\text{ d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{r}}\phi {\text{s}}1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}\phi 1}} } \right]\left[ {B_{\phi } } \right]} } {\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{r}}\psi {\text{s}}1}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}\psi 1}} } \right]\left[ {B_{\psi } } \right]} } {\text{ d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{rts}}1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}1}} } \right]\left[ {B_{{{\text{ts}}}} } \right]} } {\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rrs}}1}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}1}} } \right]\left[ {B_{{{\text{rs}}}} } \right]} } {\text{ d}}x\,{\text{d}}y \\ & \left[ {K_{{{\text{ts}}1}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{ts}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}1}} } \right]\left[ {B_{{{\text{ts}}}} } \right]} } {\text{ d}}x\,{\text{d}}y;\quad \left[ {K_{{{\text{rts}}3}}^{{\text{e}}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{{\text{rs}}}} } \right]^{{\text{T}}} \left[ {D_{{{\text{s}}3}} } \right]\left[ {B_{{{\text{ts}}}} } \right]} } {\text{ d}}x\,{\text{d}}y \\ & \left\{ {F_{\psi } } \right\} = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {N_{\psi } } \right]^{{\text{T}}} Q^{\psi } } } {\text{ d}}x\,{\text{d}}y;\left\{ {F_{\phi } } \right\} = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {N_{\phi } } \right]^{{\text{T}}} Q^{\phi } } } {\text{ d}}x\,{\text{d}}y; \\ & \left\{ {F_{m} } \right\} = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {N_{{\text{t}}} } \right]^{{\text{T}}} \left[ {\begin{array}{*{20}c} {p_{x} } & {p_{y} } & {p_{z} } \\ \end{array} } \right]} } {\text{ d}}x\,{\text{d}}y. \\ \end{aligned}$$
(26)

The various rigidity matrices contributing to Eq. (26) can be denoted as follows:

$$\begin{aligned} & \left[ {D_{{{\text{b}}1}} } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{{C_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{bbNL}}1}} } \right] = \frac{1}{4}\left[ {D_{{{\text{b}}1}} } \right];\quad \left[ {D_{{{\text{bNL}}1}} } \right] = \frac{1}{2}\left[ {D_{{{\text{b}}1}} } \right];\quad \left[ {D_{{{\text{b}}2}} } \right] = \int\limits_{ - h/2}^{h/2} {z\left[ {\overline{{C_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z \\ & \left[ {D_{{{\text{bNL}}2}} } \right] = \frac{1}{2}\left[ {D_{{{\text{b}}2}} } \right];\quad \left[ {D_{{{\text{b}}3}} } \right] = \int\limits_{ - h/2}^{h/2} {z^{2} \left[ {\overline{{C_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{b}}4}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{1} z^{3} \left[ {\overline{{C_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{bNL}}4}} } \right] = \frac{1}{2}\left[ {D_{{{\text{b}}4}} } \right] \\ & \left[ {D_{{{\text{b}}5}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{1} z^{4} \left[ {\overline{{C_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{b}}7}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{1}^{2} z^{6} \left[ {\overline{{C_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{b}}\phi 1}} } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{{e_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z; \\ & \left[ {D_{{{\text{bNL}}\phi 1}} } \right] = \left[ {D_{{{\text{b}}\phi 1}} } \right];\quad \left[ {D_{{{\text{b}}\phi 2}} } \right] = \int\limits_{ - h/2}^{h/2} {z\left[ {\overline{{e_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{b}}\phi 4}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{1} z^{3} \left[ {\overline{{e_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z; \\ & \left[ {D_{{{\text{b}}\psi 1}} } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{{q_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{bNL}}\psi 1}} } \right] = \left[ {D_{{{\text{b}}\psi 1}} } \right]; \\ & \left[ {D_{{{\text{b}}\psi 2}} } \right] = \int\limits_{ - h/2}^{h/2} {z\left[ {\overline{{q_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\left[ {D_{{{\text{s}}1}} } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{{C_{{\text{s}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{b}}\psi 4}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{1} z^{3} \left[ {\overline{{q_{{\text{b}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z; \\ & \left[ {D_{{{\text{s}}3}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{2} z^{2} \left[ {\overline{{C_{{\text{s}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{s}}5}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{2}^{2} z^{4} \left[ {\overline{{C_{{\text{s}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{s}}\phi 1}} } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{{e_{{\text{s}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z; \\ & \left[ {D_{{{\text{s}}\phi 3}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{2} z^{2} \left[ {\overline{{e_{{\text{s}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{s}}\psi 1}} } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{{q_{{\text{s}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{{{\text{s}}\psi 3}} } \right] = \int\limits_{ - h/2}^{h/2} {c_{2} z^{2} \left[ {\overline{{q_{{\text{s}}} }}^{{{\text{fg}}}} } \right]} {\text{d}}z; \\ & \left[ {D_{\phi \phi } } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{\eta }^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{\psi \psi } } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{\mu }^{{{\text{fg}}}} } \right]} {\text{d}}z;\quad \left[ {D_{\phi \psi } } \right] = \int\limits_{ - h/2}^{h/2} {\left[ {\overline{m}^{{{\text{fg}}}} } \right]} {\text{d}}z. \\ \end{aligned}$$
(27)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mahesh, V., Harursampath, D. Large deflection analysis of functionally graded magneto-electro-elastic porous flat panels. Engineering with Computers 38 (Suppl 2), 1615–1634 (2022). https://doi.org/10.1007/s00366-020-01270-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01270-x

Keywords

Search

Navigation