1 Introduction

A beam grillage is a structure made of a planar network of connected beams loaded normally to their plane. The geometrical configuration and the mutual moment-resisting connection between elements allow flexural and torsional resisting mechanisms to develop within the grillage, with general small displacements and a great ability in load redistribution. For this reason, this type of structure is widely used in civil constructions, such as in bridges, and in marine structures [1]. Even in small grillage structures, the number of degrees of freedom is large enough that simple mathematical expressions for displacement and forces are difficult to formulate. Although the studies on the behavior of structures loaded with out-of-plane forces date back to the nineteenth century [2], in the sixties and the seventies the major improvements on the design of grillage structures are found. Holmes and Ray-Chaudhuri [3] propose a limit analysis for determining the ultimate load of grillages, while minimum weight and optimization studies were first proposed by Rozvany [4]. More recent studies focus on the dynamic behavior [5] or on the optimization of foundation grillages [6].

The so-called grillage analogy is a widely adopted strategy for solving structures with out-of-plane loads, such as in bridge superstructures analysis [7]. The validity of such approach has been validated by comparing numerical analyses and experimental data, such as in [8]. Grillage structural schemes have been also introduced for modeling elastic continua [9]. With reference to the numerical methods for solving the structures, before the introduction of FEM, matrix analysis was the usual mathematical tool for studying beam grillage [10]. As largely diffused in civil and mechanical engineering, beam grillage structures can be made of various materials: concrete, steel, timber or composite material and can be subjected to various types of loading, including moving forces [11] or impacts and blasts [12]. It is worth to be mentioned that, although made of a planar network of beams, load transfer in grillage of reciprocal beams is related only to the flexural mechanisms, as the elements are supported one each other [13].

From a topological point of view, the network of beams is a statically indeterminate structure. Such structural schemes are characterized by a complex behavior [14], in which the distribution of stresses is driven by preferential force paths, which emerge when the structure is damaged. As reported in previous works, the study of the final damaged configuration is consistent with the structural degradation process and simplifies some evaluations on damage tolerance and robustness [15]. Besides general considerations on systems of beams, the redistribution capacity of grillage structures is influenced by the support conditions. Such dependency has been highlighted in the studies by Rozvany [16], where the optimal beam layouts depends on the boundary conditions of the grillage.

As already mentioned, grillage structures are widely adopted in civil engineering works, in particular in bridge decks. In particular cases, say in Gerber girders, the span is suspended over two cantilevers, which act as supports [17]. Half-joint beams are adopted not to modify the total beam depth. Relevant failures in the past, e.g., the collapse of Annone SS36 overpass bridge in October 2016 in Italy [18] due to an anomalous load configuration, construction and maintenance issues, suggest that the integrity of Gerber girder supports is a primary requirement for the robustness of the suspended span. To this aim, several studies concentrated on the failure mechanisms of the main beams at the support [19, 20], but disregarded the specific analysis of the failure of the support itself, which requires a detailed design and maintenance during the service life of the structure [21]. For concrete structures, the behavior of half-joints depends on the arrangement and amount of reinforcements, and the quality of the concrete [22, 23]. The forensic analysis of the failure of Annone overpass highlighted that cracking and corrosion on the reinforcement bars caused a reduction of the bearing capacity of one support that initially failed [18]. Meanwhile, the investigations showed that, in the decades preceding the failure, the reduction of reinforcement area caused a progressive settlement of the supporting half-joint. This result is in perfect agreement with the results of Desnerck and colleagues [20, 22], who pointed out an evidence of a reduction of the vertical stiffness of damaged supports, which are fragile components that have not to fail in a capacity design.

The literature analysis highlights that several researches attempting to study the robustness of grillage structures with damaged beams are present, e.g., [24, 25]: in such analyses, the main focus is on the structure itself and its failure, under the hypothesis of perfect supports. On the contrary, limited attention has been devoted to the effects on the grillage of the modification of the capacity of the supports. Considering that half-joint components are hard to inspect [26], the understanding of the effects on the grillage of a change in the supporting condition would help in the structural health monitoring of the supporting structure. To this aim, the present paper deals with the behavior of a beam grillage structure with non-rigid supports, which are here modeled with elastic springs. In particular, the attention is put towards a local reduction of the stiffness of one support and the resulting effects on the structure, with the focus on the support displacement and reaction forces. The results of the study are of primary interest for the design of grillage structures on non-uniform supporting conditions and for the design and data interpretation issued from structural health monitoring of existing structures subjected to aging phenomena and degradation.

2 Method

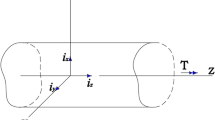
The analysis of beam grillage structures accounts both the flexural and the torsional characteristics of the elements. In the present analysis, a simple rectangular structure made of three main beams of length \(\ell \) and orthogonal transverse beams of length w at both ends is considered, as shown in Fig. 1 where the main and transverse beams are named as M and T, respectively. The grillage is subjected to a vertical uniform load q distributed along the main beams, only. The system is supported on vertical springs, to simulate the axial stiffness of the ground (if the grillage is part of a foundation system) or of a substructure (to simulate supported floors and bridge decks). The system is horizontally constrained at each node, as illustrated in the box of Fig. 1.

Fig. 1
figure 1

Sketch of the reference grillage

Full size image

The behavior the system depends on the mechanical properties of the elements, the supports, and on the geometry of the grillage. In the present analysis, the main beams are identical. Similar consideration holds for the transverse beams. The flexural and the torsional rigidities of the main beams are named as \(EI^m\) and \(GJ^m\), where E and \(G=E/\left[ 2\left( 1+\nu \right) \right] \) are the elastic and tangential elastic moduli, respectively, \(I^m\) and \(J^m\) are the flexural and torsional inertias of the cross-section of the main beam. Similar consideration holds for the transverse beams, which are characterized by superscript \(^t\), i.e., \(EI^t\) and \(GJ^t\). The vertical stiffness of the i-th support is named as \(k_i\).

In a dimensional analysis framework, only two physical dimensions are present in the problem: the length \(\left[ L\right] \) and the force \(\left[ F \right] \). Flexural and torsional rigidities have the physical dimensions of \(\left[ FL^2\right] \), the vertical stiffness and the distributed load of \(\left[ FL^{-1} \right] \). Following Buckingham’s \(\Pi \)-theorem [27], two quantities can be chosen as repeated quantities and serve for the creating dimensionless quantities. In the present analysis, the length of the main beam \(\ell \) and the flexural rigidity of the main beam, \(EI^m\), are chosen as repeating terms. Thus, the following dimensionless parameters can be formulated:

$$\begin{aligned} \begin{aligned} \rho&=\frac{w}{\ell }&\eta&=\frac{EI^t}{EI^m}\\ \mu ^\bullet&=\frac{GJ^\bullet }{EI^\bullet }&\omega&=\frac{q\ell ^3}{EI^m},\\ \end{aligned} \end{aligned}$$
(1)

where the bullet stands for either the main or the transverse beam (\(\bullet =m,t\)). If the beams are rectangular, one can draw a relationship between torsional and flexural inertias, in such a way that \(\mu ^\bullet \) can be rewritten as

$$\begin{aligned} \mu ^\bullet =\frac{6\beta \left( \lambda _\bullet \right) }{\lambda _\bullet ^2\left( 1+\nu \right) }, \end{aligned}$$
(2)

where \(\lambda _\bullet \) is the slenderness of the cross-section of the beam, i.e., the ratio between beam depth and beam width. Following Timoshenko [28], the term \(\beta \left( \lambda _\bullet \right) \) represents the numerical factor for computing torsional rigidity (\(\beta = 1/3\) when \(\lambda \rightarrow \infty \)). Table 1 reports the values of \(\mu ^\bullet \) for various rectangular beams for \(\nu =0.3\).

Table 1 Values of \(\mu ^\bullet \) for various depth-to-width ratios for rectangular beams
Full size table

Using the same repeating terms, the vertical stiffness \(k_i\) of the i-th support can be rewritten as

$$\begin{aligned} \xi _i=\frac{k_i \ell ^3}{EI^m}. \end{aligned}$$
(3)

The study herein performed intends to model the behavior of the grillage when the stiffness of one of the supports differs from the one of the others. As a limit case, considering that the vertical stiffness of one support is null corresponds to the complete removal of the support. One can rethink the stiffness reduction of this model as either a local lack of capacity in soft soils for foundation grillages, a reduction of the rigidity of the elastomeric support of dapped-end beams or a degradation of the half-joint connection in Gerber suspended spans, etc.

To fully investigate the effects of modifications on the vertical stiffnesses of the supports on the grillage, several configurations are considered, as listed below.

  1. 1.

    The damage occurs on a corner support. In this case, a non-symmetric damage configuration is studied. Fig. 1 depicts, on the right-hand side, a plan view of the grillage. Five nodes, i.e., \(i=1/3,5,6\), are supported by intact springs with stiffness k (i.e., \(k_1=k\) and so forth), while the node 4 is supported by a defective spring with stiffness \(k_4=k/10\). Consequently, it results that \(\xi _4=\xi /10\), where \(\xi \) is the dimensionless support stiffness of nodes 1, 2, 3, 5 and 6. The results are reported in Sect. 3.1.

  2. 2.

    The damage occurs on a central support. In this case, a symmetric damage configuration is analyzed. With reference to Fig. 1, node 5 is supported by a defective spring with stiffness \(k_5=k/10\), while nodes 1/3, 4 and 6 are supported by intact springs with stiffness k. As in the previous case, \(\xi _5=\xi /10\), where \(\xi \) is the dimensionless support stiffness of nodes 1, 2, 3, 4 and 6. The results are reported in Sect. 3.2.

  3. 3.

    An additional transverse beam is added to the grillage. In this case, the new transverse beam connects the midpoints of the main beams. The properties of the transverse beam as equal to those of the transverse beams at the ends. The results are reported in Sect. 3.3.

  4. 4.

    The stiffness of the defective support changes between 0.9k and 0.1k. To study the evolution of the behavior of the grillage with the increment of the damage, i.e., the reduction of support stiffness, several damage steps are considered. The analysis is performed considering that the defective support is on node 4. Thus, various stiffnesses are considered: \(\xi _4=\left( 0.9\rightarrow 0.1\right) \xi \), where \(\xi \) is intact spring dimensionless stiffness. The results are reported in Sect. 3.4.

The numerical analyses were performed on MATLAB coupled with OpenSees [29] routines varying the geometry of the grillage, i.e., parameter \(\rho \) in the range \(\left[ 0.05; 1\right] \), transverse-to-main beam flexural rigidities, i.e., parameter \(\eta \) in the range \(\left[ 0.2;1\right] \), and intact spring dimensionless stiffness \(\xi \) in the range \(\left[ 10^{-2};10^{6}\right] \), considering different beam cross-section geometries (square and rectangular).

3 Results

The vertical displacement of the supports \(v_i\) and the reaction forces \(R_i\) can be written in a dimensionless form. To highlight the behavior of the structure subjected to a local support stiffness reduction, support reactions are compared with the forces that an intact structure would experience. Applying Buckinham’s \(\Pi \)-theorem, a dummy variable \({\tilde{\psi }}_i\) is formulated:

$$\begin{aligned} {\tilde{\psi }}_i=\frac{R_i \ell ^2}{EI^m}. \end{aligned}$$
(4)

Considering that the reactions in an intact grillage are identical and equal to \(q \ell /2\), the normalized dimensionless reaction \(\psi _i\) is equal to \(\psi _i=2{\tilde{\psi }}_i/\omega \).

The vertical nodal displacements, \(v_i\), are normalized with respect to the displacements that would be observed in a structure if the supports would have equal stiffness k. The normalized dimensionless displacement \(\delta _i\) is equal to

$$\begin{aligned} \delta _i=\frac{2v_i k}{q\ell }=\left( \frac{v_i}{\ell }\right) \frac{2\xi }{\omega } \end{aligned}$$
(5)

where the term in the round brackets is the dimensionless displacement according to Buckingham’s \(\Pi \)-theorem. Downwards displacements are positive.

3.1 Non-symmetric damage configuration

Figure 2 shows the values of the normalized reactions and displacements for both square (\(\lambda _\bullet =1\), with continuous lines) and rectangular (\(\lambda _\bullet =10\), with dashed lines) cross-sections. The non-symmetric damage configuration accounts for the damage on the corner support (node 4).

Fig. 2
figure 2

Damage on support no.4. Normalized reactions (top) and support displacements (bottom) in a grillage with \(\eta =0.1\) and \(\rho =0.5\) in a range \(\xi =\left[ 10^{-2};10^6\right] \). Continuous curves relate to a grillage with square (\(\lambda _\bullet =1\)) elements, while dashed lines to a structure with rectangular (\(\lambda _\bullet =10\)) elements

Full size image

The results are related to the geometrical configuration with \(\eta =0.1\) and \(\rho =0.5\). It clearly emerges that the value of \(\xi \) influences the values of reactions and displacements. In particular, three regimes are individuated. For stiffnesses smaller than a threshold value, say \(\xi =1\) for square cross-section structure, approximatively constant values are reported. Similarly, for large \(\xi \), say \(\xi >10^4\), all the normalized reactions are similar and close to 1, while all the normalized displacements are unitary, except the one of node 4 with the defective spring for which a value 10 (equal to \(\xi /\xi _4\)) is observed. In between, a transition regime between the two limit situations is observed, with reactions reaching local maxima or minima, clearly evident in the reactions of nodes 5 and 6 of the rectangular cross-section structure. Similar considerations can be drawn for displacements. The case proposed in Fig. 2 is just an example of what it is observed for other \(\eta \) and \(\rho \) values.

The trends show the intimate dependency between springs stiffness and grillage behavior and how the stiffness of the supports, once locally damaged, can influence force redistributions in the grillage. To identify the displacement regimes within the grillage, a critical analysis of the displacements is performed. Fig. 3 depicts the normalized displacements for a structure with square cross sections having \(\eta =0.5\), \(\rho =0.5\). Three different behaviors are observed. Starting from the right-hand side, i.e., large \(\xi \), a drop-like response (named as Dr) emerges, with node 4 experiencing the largest displacements, only. The sketch below depicts this structural response which is observed for a large range of \(\xi \)-values, for \(\xi \ge 2.2\cdot 10^{4}\). For smaller \(\xi \)-values, a twist-like behavior (Tw) is observed: the vertical displacement of node 2 is smaller than the one of node 3, with \(\delta _2<1\), meaning that, apparently, the node goes up. In an opposite way, the vertical displacement of node 6 is smaller than the one of node 5, with \(\delta _6<1\). It clearly emerges that a part of the grillage undergoes twisting, as sketched in the bottom of Fig. 3. This structural response occurs for \(5.1\cdot 10^1\le \xi <2.2\cdot 10^{4}\). For smaller values, it results that \(\delta _2<\delta _3\) and the structural response of the grillage tends to a uniform rotated configuration (Un), as reported in the bottom-left sketch of Fig. 3.

Fig. 3
figure 3

Normalized displacements for a grillage with \(\eta =0.1\), \(\rho =0.5\) and \(\lambda _\bullet =1\) (square cross-section). Three displacement regimes are individuated: uniform rotation (Un), twist (Tw) and drop (Dr). Note that y-axis scale is in a reverse order; for the colors of the supports refer to Fig. 1

Full size image

3.2 Symmetric damage configuration

Figure 4 depicts the values of the normalized reactions and displacements for both square (\(\lambda _\bullet =1\), with continuous lines) and rectangular (\(\lambda _\bullet =10\), with dashed lines) cross-sections. The symmetric damage configuration accounts for the damage on the support of the central node (node 5).

The results are related to the geometrical configuration with \(\eta =0.1\) and \(\rho =0.5\). As expected from the previous analysis related to corner damage, the results are affected by the value of \(\xi \). Three regimes can be individuated. For \(\xi <1\), the values of support displacement and reactions are constant and almost independent from \(\xi \). The normalized reactions in nodes 4 and 6 compensate the drop on node 5 drops to roughly \(\psi _5=0.15\), while the effects on the opposite nodes are completely negligible, i.e., \(\psi _i\approx 1\) for \(i=1,2,3\). Similar trends are observed for \(\xi >10^4\), where all the reaction forces are equal and all the displacement, except the one of node 5, are unaffected by the defective support. In between, i.e., \(1<\xi <10^4\), a transition is observed. The central support on the opposite side is pushed down with a larger reaction force, while the corner support (nodes 1 and 3) raises, resulting in a reduction of the reaction.

Fig. 4
figure 4

Damage on support no.5. Normalized reactions (top) and support displacements (bottom) in a grillage with \(\eta =0.1\) and \(\rho =0.5\) in a range \(\xi =\left[ 10^{-2};10^6\right] \). Continuous curves relate to a grillage with square (\(\lambda _\bullet =1\)) elements, while dashed lines to a structure with rectangular (\(\lambda _\bullet =10\)) elements. The curves related to nodes/reactions 4 and 6 are superposed; similarly, the curves related to nodes/reactions 1 and 3 are superposed

Full size image

Observing the displacement regimes reported in Fig. 5, a folding-like (Fl) regime is observed since nodes 1 and 3 moves upwards, while node 2 goes down with respect to the undamaged position, for which \(\delta _i=1\). A similar trend, shifted downwards is observed for nodes 4, 5 and 6. This regime is observed in the interval \(1<\xi <10^4\). For lower \(\xi \) a uniform tilting (Un) emerges, while for larger \(\xi \) a drop (Dr) of node 5 is noted. As expected, the reaction forces and displacement regimes are symmetrical with respect to the longitudinal axis of the grillage (i.e., the line passing through nodes 2 and 5).

Fig. 5
figure 5

Normalized displacements for a grillage with \(\eta =0.1\), \(\rho =0.5\) and \(\lambda _\bullet =1\) (square cross-section). Three displacement regimes are individuated: uniform tilting (Un), folding (Fl) and drop (Dr). Note that y-axis scale is in a reverse order; for the colors of the supports, refer to Fig. 1

Full size image

3.3 Effects of additional transverse beams

The effect of additional transverse beams is highlighted by comparing reaction forces and nodal displacements with and without an additional transverse beam. The damaged configuration accounts for a reduction of vertical stiffness on node 4, namely \(\xi _4=\xi /10\). Figure 6 shows the results of the analysis: thin curves refer to a grillage structure without the transverse beams, while thick curves to a structure with transverse beams. It is noted that the observed trends are not affected by the presence of the additional elements: considering that the threshold between uniform (Un) and twisting-like (Tw) behaviors corresponds to the \(\xi \) for which \(\delta _2=\delta _3\), or alternatively, \(\psi _2=\psi _3\), the presence of the additional transverse beams moves rightwards the threshold point. In fact, thin yellow-red curves of Fig. 6 intercept at \(\xi \approx 15\), while thick yellow-red curves at \(\xi \approx 24\).

Fig. 6
figure 6

Damage on support no.4. Normalized reactions (top) and support displacements (bottom) in a grillage with \(\eta =0.1\), \(\rho =0.5\) and \(\lambda _\bullet =1\) (square cross-section) in a range \(\xi =\left[ 10^{-2};10^6\right] \). Thick curves relate to the grillage with additional transverse beams

Full size image

3.4 Evolution of the effects with increasing damage

Figure 7 plots the vertical displacements of the six nodes on a grillage subjected to a vertical stiffness reduction on support no.4. Various damaged-to-non damaged stiffness ratios, namely \(\Xi =\xi _4/\xi \), are considered in the range \(\left[ 0.1;1\right] \). For \(\xi _4/\xi =1\), thick continuous black line, the support is not damaged: it clearly emerges that the structural behavior of the grillage is not affected by the stiffness of the supports (which, in this case, are equal). For \(\xi _4/\xi =0.1\), i.e., \(\xi _4=\xi /10\), thick dashed black line, the curves are identical to the ones depicted in the bottom plot of Fig. 2. Intermediate curves refer to intermediate damaged stiffnesses. An identical behavior is observed in each support: the intermediate curves have the same trend of the thick dashed black curves and the values of the displacements \(\delta _i\) are scaled. This shows that the magnitude of the damage does not affect the observed trends, but it magnifies the effects, only.

Fig. 7
figure 7

Damage on support no.4. Normalized support displacements in a grillage with \(\eta =0.1\) and \(\rho =0.5\) with square cross-section (\(\lambda _{\bullet }=1\)) in a range \(\xi =\left[ 10^{-2};10^6\right] \). Each curve corresponds to a damaged-to-non damaged stiffness ratio, \(\xi _4/\xi \). Note that y-axis is in reverse order

Full size image

4 Discussion

The results presented in the previous section (Sec. 3) show that the response of the grillage to the local damage is affected by the properties of the grillage itself (flexural and torsional rigidities of main and transverse beams and the size of the grillage) and by the stiffnesses of the supports, either intact or damaged. Although simple, the considered grillage is able to highlight several basic behaviors that emerge when the supports are damaged. (The results herein presented can be extended to other geometrical arrangements, involving more than three main beams.) With the tentative of interpreting the different responses of the non-symmetric damage configuration, the drop-like response (Dr) emerges as the stiffness of the supports, either intact or defective, is larger than the rigidity of the grillage. In this situation, the grillage results flexible and accommodates the damage by perfectly redistributing the loads. This means that the structure is tolerant with respect to the damage, i.e., the reduction of stiffness of one support, as the effects are confined to the node in which the reduction is acting. In the twist-like behavior (Tw), the flexural stiffness of the transverse beams redistributes the forces to nodes 5 and 6. The former is pushed down and a greater reaction occurs, the latter experiences a reduction in the reaction force. The response on nodes 4, 5 and 6 has the effect of reducing the reactions on the opposite side of the grillage: the central support (node 2) tends to be unloaded and moves up. Observing Fig. 2, it can be noted that this behavior is observed both in square and in rectangular cross-sections structures. The uniform behavior (Un) emerges when the rigidity of the grillage is larger than the stiffness of the supports. In this regime the structure keeps its integrity by tilting in a rigid way. With reference to the symmetric damage configuration, similar considerations can be drawn. It must be noted that a sort of equilibrium emerges on the main beams in the folding (Fd) regime. In other words, the reaction force in node 4 increases and the reaction force in node 1 decreases; similarly, it occurs in nodes 3/6. This behavior, which can be observed in Fig. 5, can be easily identified in the twisting-like regime in Fig. 3 in nodes 2/5 and 3/6. The transition regimes (Tw and Fd) represent a good match in terms of grillage and support stiffness as the whole system acts in redistributing the effects of local damage.

The analysis of the evolution of the effects on the grillage with the increase of the damage, i.e., the increment of parameter \(\Xi \), illustrates interesting trends on the complexity of the coupled system made by the grillage and supports. To highlight the trends, differences between nodal displacements in the damaged and undamaged configurations were computed and their ratio was averaged over all the supports, as

$$\begin{aligned} \Omega =\frac{1}{6}\sum _i \frac{\delta _i^{\Xi }-1}{\delta _i^{0.1}-1}, \end{aligned}$$
(6)

where \(\delta _i^{0.1}\) corresponds to the vertical displacement of the i-th node for \(\Xi =0.1\), i.e., \(\xi _4=\xi /10\), and \(\delta _i^{\Xi }\) is the vertical displacement of the i-th node for a generic \(\Xi \) value. This represents a measure of the scaling between each curve of Fig. 7 and the corresponding curve for \(\Xi =0.1\). Figure 8 shows the values of \(\Omega \) for various \(\xi \) on a grillage structure with damaged support no.4.

Fig. 8
figure 8

Values of the ratio \(\Omega \) computed with Eq. (6) for a grillage with \(\eta =0.1\), \(\rho =0.5\) and square cross-section (\(\lambda _{\bullet }=1\)), damaged on support no. 4

Full size image

It clearly emerges that the increase in damage, i.e., the reduction from \(\Xi =1\rightarrow 0.1\) does not presupposes a perfectly linear effect on the displacements. This is a result of the mutual interaction between the elements and the supports and is a common trend in statically indeterminate structures [30, 31]. Different evolutions are observed for different values of \(\xi \). For low \(\xi \) a quasi-linear trend between the ends of the curve is observed, while a pronounced nonlinear trend is noted for high \(\xi \). The observed results agree with the previous findings on statically indeterminate structures: with reference to the previous works by the Author, a linear evolution in the effects of the damage refers to a structure which is not complex, while a nonlinear trend is a evidence of structural complexity [30, 31]. In this sense, for high \(\xi \), the grillage tends to behave as “complex”, following the definition provided by De Biagi and Chiaia [14]. As a matter of fact, the three beams are independent one with respect to the others, as the transverse beams are not able to redistribute the loads and a variation in the stiffness of one support affects the corresponding beam, only. Half beam and the corresponding support constitute the load path. On the contrary, for low \(\xi \), a redistribution of the effects of the damage occurs as all the elements (and non-damaged supports) participate to load transfer and bearing capacity of the system. Here, the behavior is ruled by the equivalent stiffness of all the supports as the grillage behaves as a quasi-rigid-like body. In this sense, the linear reduction of the stiffness of support no.4 implies a linear reduction of the equivalent stiffness of all the supports, with a consequent quasi linear evolution of the effects.

5 Conclusions

The present study is devoted to the analysis of the response of a simple grillage structure lying on spring supports. Several important considerations can be drawn. First, the behavior of the grillage on spring supports does not depend on the structural arrangement of the grillage itself, but also on the stiffness of the supports. In particular, the response of the structure is largely affected by the stiffness of the intact supports rather than the stiffness of the damaged support. Two ultimate responses are observed: a drop-like behavior when the grillage accommodates the damage showing robust properties and a uniform-like behavior when the rigidity of the grillage is larger compared to the stiffness of the supports, either intact or damaged. Intermediate behaviors are found with twist-like and folding-like displacement patterns depending on the location of the damaged support. The robustness considerations are supported by the analysis of the evolution of the effects of the damage on the response of the structure following an approach already proposed by the Author. Evidences of structural complexity and damage tolerance are shown when the support is more rigid than the structure.

The outputs of the present research are the bases for future studies for assessing the robustness of grillage structures towards unexpected damage scenarios. Moreover, the results are of relevant importance in structural health monitoring of civil engineering structures. A detailed knowledge of the expected displacements and of the mutual effects between components, not only related to the grillage, would provide a better awareness in the design of a monitoring system and in the interpretation of the data.