1 Introduction

The conversion of ambient vibrations into small amounts of electric energy (termed energy scavenging or energy harvesting) has been the subject of numerous investigations during the last two decades. As it is described in the work of Stephen [30], a major motivation for the research on energy harvesting systems (EH-systems) is the development of energy-autonomous low-power microelectromechanical systems (MEMS). The basis structure of such an EH-system usually consists of a mechanical component that is attached to the vibrating host-structure, so that the vibration leads to an external base excitation of the EH-system [28]. If the mechanical structure is a linear resonator and the excitation has harmonic characteristics, the efficiency of the system relies strongly on the matching between the excitation frequency and the natural frequency of the EH-system [26]. A promising method to overcome this limitation lies in the utilization of a nonlinear restoring force that can be used to broaden the frequency range, in which the EH-system operates efficiently [7]. As shown in [16], the broadening effect is especially strong, if the nonlinearity is designed in such a way that the system develops multiple stable equilibrium positions. Since its introduction in [5], the concept of bi-stability (two stable and one unstable equilibrium position) receives a lot of interest, as can be seen from the comprehensive review article [8] and the references therein. The concept was then developed further for the case of tri-stable [38] systems (three stable and two unstable equilibrium positions) and more recently to the case of general multi-stable systems [11].

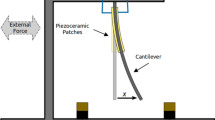
The present paper focuses on a bistable magnetoelastic system consisting of a cantilever beam. The bistability is introduced by two magnets close to the tip, while the type of multistability depends on the position and strength of the magnets. For the conversion of mechanical to electrical energy while using the set-up as an EH-system, generally piezoceramics are bonded close to the bearing. The focus of the present paper is the description of the nonlinear restoring forces, with application of a regression based method for the identification of the governing equations of motion. Therefore, the piezoceramics are omitted with all their properties, i.e., stiffness, mass and electromechanical coupling with the connected electric circuit in both experiments and modeling.

The modeling of the magnetoelastic forces is an ongoing challenge as will be described shortly in the following and more in detail in Sect. 2. Classical modeling [20] includes discretization of the beam, the assumption of a cubic restoring characteristics and the determination of the corresponding parameters. The so-called heuristic method for the determination of the parameters uses the stable equilibrium positions and the natural frequency of small amplitude vibrations around them, see e.g., [12, 24, 31]. Therefore, vibrations around one equilibrium position (intrawell solutions) might show better agreement as large amplitude vibrations around both equilibria (interwell solutions), as will be demonstrated in the following.

The present paper extends the work of the cumulative doctoral thesis of Noll [21] based on the papers [22, 23] and [24] and the underlying corresponding experimental results and investigations therein. In this prior work, attempts to model directly the restoring forces from simulations of the magnetic field ( [23] and sources cited therein) have been proven to be very hard and do not show satisfying agreement to experimental observations.

To overcome these problems, methods based on regression for identifying nonlinear models by differential equations and corresponding parameters are applied in the present paper to get an appropriate modeling of the experimentally observed behavior.

The subject of the investigation has some similarities with the one in [37], because it also examines a parameter identification of a multistable EH-system. However, [37] is a theoretical investigation that focuses on sparse identification under stochastic excitation and is not concerned with the validity of models with respect to experimental data.

Parameter identification techniques of nonlinear dynamical models have been the subject of research since many years [18]. A large number of different approaches was developed representing the restoring characteristic and tested on simulated data, e.g., Duffing-type equations [17, 34]. Dynamical models at that time have already shown good agreement with experimental data [15], if, apart from a few adjustable parameters, the general form of the equations is known. Therefore, one later on upcoming challenge was to limit the complexity of such models. Corresponding attempts have been done in 1987 by minimizing the model’s entropy [4], as well as in recent years by sparse regression [3, 29].

The paper is arranged as follows. In Sect. 2, a brief review is given on the state-of-the-art modeling of the bistable system and on the experimental setup used for the prior measurements of time series. In Sect. 3, first, the regression method is introduced and simulation results of different models are compared to experimental data. Subsequently, the method of regression-based modeling is introduced and progressively applied to the experimental data. Cubic and quintic modeling approaches as well as the inclusion of constraints are investigated. Furthermore, simulation results of the obtained models are compared with the heuristic model and experimental data. Section 4 gives corresponding conclusions, and Sect. 5 shows an outlook into further investigations.

2 Considered system, state-of-the-art modeling and experimental set-up

The system under consideration is a cantilever beam mounted on a frame with uni-axial base excitation. The bistability is introduced by magnets placed symmetrically close to the tip of the beam at the frame. In this section, some comments on the state-of-the-art modeling are given, and the experimental set-up is described.

2.1 State-of-the-art modeling

As stated above, the characteristic feature of the bistable system under consideration is the nonlinear restoring force, which leads to the appearance of two stable non-trivial equilibrium positions as well as a destabilization of the trivial equilibrium position. A corresponding system (also without piezoceramic elements) has already been analyzed in theory and experiment by Moon and Holmes in their seminal work [20] published in 1979. What makes this work so important is that the model developed therein is still commonly used until this day (see e.g., [6, 9, 35]), although there are a number of restrictions in its applicability which are direct results from the assumptions that are made.

The first assumption is that the system can be discretized using only the first eigenfunction of the corresponding linear system. This assumption is supposed to be valid, if the system oscillates with small amplitudes in proportion to the length of the beam and especially, if the excitation frequency is close to the eigenfrequency of the corresponding eigenfunction. For example, in the case of white noise or other broad band excitation, a single discretization mode may not be enough. A corresponding extended modeling was introduced in [12]. It was also shown in [23] experimentally that small parts of the second beam eigenshape are present in this nonlinear system even in the case, when the beam is excited close to its first natural frequency.

Furthermore, it is also assumed in minimal modeling according to [20] that the nonlinear restoring force has the basic shape of a cubic polynomial (the quadratic term vanishes due to the symmetry of the system) acting only on the beam tip. A cubic restoring force is in fact the minimum polynomial order required to represent the bistable behavior.

The resulting model has the form of a Duffing oscillator with viscous linear damping, a negative linear \((\alpha <0)\) and positive cubic stiffness

$$\begin{aligned} \ddot{x}(t)+\delta {\dot{x}}(t) + \alpha x(t) + \beta x^3(t) = f(t). \end{aligned}$$
(1)

Furthermore, the system is generally excited by an external excitation. The modeling that was proposed in [20] and later on used in [12, 21, 31] is denoted as “Heuristic Model,” abbreviated as HM in the following. It determines the coefficients of the equation in that way that the position of the stable equilibrium \(x=\pm x_{0}\) (approximately same absolute values due to the symmetric structure of the system) as well as the frequency \(f_{x_0}\) of small free oscillations around those equilibrium positions match measured values of the experimental apparatus. Consequently, the parameters \(\alpha \) and \(\beta \) can be obtained from the corresponding conditions

$$\begin{aligned} x_{0}=\sqrt{\frac{-\alpha }{\beta }},~~~2 \pi f_{x_0}=\sqrt{-2\alpha }. \end{aligned}$$
(2)

A linearized damping ratio \(\delta \) is estimated here by the decay rate of free vibrations of the beam structure. Thus, any kind of electromagnetic dissipation is neglected.

2.2 Experimental setup and dimensions

As has been mentioned before, the experimental results stem from the underlying work of [21]. The corresponding experimental setup is briefly described below. The used magnetoelastic bistable system mainly consists of a ferromagnetic cantilever beam (length \(l=250\,\textrm{mm}\), mass per length \(\mu = 0.163\,\textrm{kg}\,\textrm{m}^{-1}\), bending stiffness \(EI=140\,\textrm{N}\,\textrm{m}^{2}\)), two permanent magnets made of neodymium (NdFeB) and a non-ferromagnetic frame of aluminum. As shown in Fig. 1, the magnets are symmetrically placed to the undeflected position of the beam tip \(x=0\). All relevant dimensions of the systems configuration are summarized in Table 1.

Fig. 1
figure 1

Dimensions of the experimental beam structure

Full size image
Table 1 Dimensions of the systems components
Full size table

Following the procedure described in Sect. 2.1, the damping ratio is determined as \(\delta = 0.3\,\mathrm {s^{-1}}\) and the frequency of free vibrations is \(f_{x_0} = 14.75\,\textrm{Hz}\) (average of both sides) [24]. System (Fig. 2) is investigated under harmonic excitation. Therefore, the entire structure \(\textcircled {{1}}\) is mounted on a vibration table \(\textcircled {{8}}\), which represents the oscillating energy source of the surrounding. The required excitation is provided by a shaker \(\textcircled {4}\). It is energized by a harmonic voltage signal adjusted at the amplifier \(\textcircled {{5}}\). Two measurement devices are used to record the input and the state of the system. On the right, a laser vibrometer \(\textcircled {{2}}\) is positioned axially in the direction of the oscillation and measures the absolute velocity of the frame, regarded as the input. Simultaneously, a laser triangulation sensor \(\textcircled {{3}}\) that is mounted on the frame measures the relative position of the beam tip x (representing the system’s degree of freedom after discretization). The sampling rate of both signals is chosen to be \(10\,\textrm{kHz}\), performed after a low-pass filter applied by the measurement box \(\textcircled {{6}}\). The experimental structure has been excited harmonically in a range 7–18 Hz with stepsize \(0.25\,\textrm{Hz}\) and under constant amplitude of \(3.81\,\mathrm {m\,s^{-2}}\) (with standard deviation of \(0.086\,\mathrm {m\,s^{-2}}\)). For comparison, the first eigenfrequency of the beam structure is at \(13.4\,\textrm{Hz}\). Ten runs were performed for each step of frequency and therefore 450 runs in total. The aim is to investigate the stationary systems response. To reduce the influence of transient oscillations, a \(60\,\textrm{s}\) measurement began after \(10\,\textrm{s}\) of unrecorded motion.

Fig. 2
figure 2

Experimental setup: \(\textcircled {{1}}\) bistable beam system and frame, \(\textcircled {{2}}\) laser vibrometer, \(\textcircled {{3}}\) laser triangulation sensor, \(\textcircled {{4}}\) shaker, \(\textcircled {{5}}\) amplifier, \(\textcircled {{6}}\) measurement box, \(\textcircled {{7}}\) laptop, \(\textcircled {{8}}\) vibration table

Full size image

2.3 Examination of the heuristic model

Considering the free vibration measurements and static constraints together with Eq. (2), the HM parameter identification applied in [21, 24] results there in the following parameters

$$\begin{aligned} \delta = 0.3\,\mathrm {s^{-1}},\quad \alpha = 4275.6\,\mathrm {s^{-2}},\quad \beta = 88.2\,\mathrm {mm^{-2}\,s^{-2}}. \end{aligned}$$
(3)

Subsequently, in [24], a comparison of the measurement data and numerical results of the model based on HM by means of bifurcation diagrams was performed. These investigations are here addressed again as new models are to be compared with the old ones.

The model obtained from HM is run again in a simulation using Matlab® ode45 under the same frequency and amplitude of harmonic excitation like in the experiment. Since the oscillator is driven by acceleration-proportional excitation while velocity is measured, time derivatives are required from the velocity signals. To prevent the amplification of noise, a mean averaging filter is applied, before taking the derivatives with central differences. The mean filter has an order of 20, i.e., 10 neighbors on both sides are considered for the averaging. Due to the high resolution of recording, this type of filtering causes only a very small negligible change in the amplitudes and prevents an additional phase shift (Fig. 3a). The noise-like result of the unfiltered acceleration signal affirms the importance of the filtering (Fig. 3b).

Fig. 3
figure 3

Filtered and unfiltered displacement and acceleration signals of an exemplary experimental result at excitation frequency \(10.25\,\textrm{Hz}\)

Full size image

For the application of the regression method in the following, several numerical derivatives are required, which are obtained by performing the same procedure. For each excitation, simulations are started in a 10-by-10 equidistant grid of initial conditions, varied by the initial displacement from \(-12.98\,\textrm{mm}\) to \(12.94\,\textrm{mm}\) and initial velocity from \(-857.89\,\textrm{mm}\,\textrm{s}^{-1}\) to \(862.38\,\textrm{mm}\,\textrm{s}^{-1}\) (highest and lowest values within the experiment or by differentiation). The transient behavior has been estimated to vanish after \(100\,\textrm{s}\) in the simulation. This time interval is chosen larger as in the experiments, because in simulation much broader sets of initial conditions are realized (some of them show a long lasting transient behavior). After the simulation, the obtained solutions, in most cases stationary solutions with exception of chaos, have been classified in three different types: intrawell solution, designated if the turning points have all positive or all negative displacement, else interwell, if there are less than 20 turning points, rounded to the first digit or else chaotic solution.

Figure 4a, b shows phase plots of the experimental results and the HM at excitation frequency 7.5 and \(11\,\textrm{Hz}\). For a comparison of similar solutions types, only the trajectories are plotted that are nearest to the experimental results with respect to the approximated mean center distance of nondimensional states

$$\begin{aligned} {\bar{d}}\approx \frac{1}{n}\sum _{i=1}^n \left( \frac{x_i}{\textrm{mm}}\right) ^2+\left( \frac{{\dot{x}}_i}{\textrm{mm}\,\textrm{s}^{-1}}\right) ^2. \end{aligned}$$
(4)

Herein, n denotes the number of data points. The plots illustrate exemplary the problems of HM adapting the parameters of small amplitude vibrations. The intrawell oscillations in Fig. 4a show a remarkable good agreement. On the other hand, there is a considerable quantitative difference in the case of interwell solutions (Figure 4a, b). This inconsistency explicitly suggests that the parameter identification mechanism in the heuristic method is not sufficient for the modeling of interwell solutions (i.e., those solutions being of importance for energy harvesting) and indicates that the damping and, as will be seen later, in particular, the nonlinear restoring characteristic are not well-represented within this model’s equation.

Fig. 4
figure 4

Phase portraits at excitation frequencies \(7.5\,\textrm{Hz}\) and \(11\,\textrm{Hz}\) obtained from the experiment (black) and simulation of the HM (blue). Lighter color: intrawell, darker color: interwell (color figure online)

Full size image

3 Application of linear regression

3.1 Fundamentals of regression-based modeling

Fundamentals of the regression method in [34] are explained by the example of free vibrations of a nonlinear oscillator with one degree of freedom. Following this, a mathematical representation of such a system is a homogeneous second-order ordinary differential equation

$$\begin{aligned} \ddot{x}(t)=h(x(t),{\dot{x}}(t)). \end{aligned}$$
(5)

The aim is to find an expression or at least a suitable approximation of the unknown function \(h(x(t),{\dot{x}}(t))\) based on available time series. Assuming that the position x, velocity \({\dot{x}}\) and acceleration \(\ddot{x}\) are accessible as real numbers at several points in time \(t_1,t_2, \ldots ,t_n\), data vectors are given as follows:

$$\begin{aligned} \textbf{x}= \left[ \begin{array}{c} x(t_1) \\ x(t_2) \\ \vdots \\ x(t_n) \end{array} \right] ,~~~ \dot{\textbf{x}}= \left[ \begin{array}{c} {\dot{x}}(t_1) \\ {\dot{x}}(t_2) \\ \vdots \\ {\dot{x}}(t_n) \end{array} \right] ,~~~ \ddot{\textbf{x}}= \left[ \begin{array}{c} \ddot{x}(t_1) \\ \ddot{x}(t_2) \\ \vdots \\ \ddot{x}(t_n) \end{array} \right] . \end{aligned}$$
(6)

Obviously, Eq. (5) is satisfied for each of their components, if the relation between \(x, {\dot{x}},\ddot{x}\) can be noted as in Eq. (6). A library matrix \(\mathbf {\varTheta }(\textbf{x},\dot{\textbf{x}})\) of, in general nonlinear, candidate functions \(g_i(x,{\dot{x}})\) for \(i=1,\ldots ,m\) and \(m<n\) can be constructed from the state vectors

$$\begin{aligned} \mathbf {\varTheta }(\textbf{x},\dot{\textbf{x}})=\left[ \begin{array}{ccc} \vec {g}_1(\vec {x},\dot{\vec {x}}),~ \vec {g}_2(\vec {x},\dot{\vec {x}}),~ \ldots ,~ \vec {g}_m(\vec {x},\dot{\vec {x}}) \end{array}\right] , \end{aligned}$$
(7)

Herein, the columns are defined by the component-wise evaluation of the candidate functions

$$\begin{aligned} \textbf{g}_i(\textbf{x},\dot{\textbf{x}}) = \left[ \begin{array}{c} g_i(x(t_1),{\dot{x}}(t_1))\\ g_i(x(t_2),{\dot{x}}(t_2))\\ \vdots \\ g_i(x(t_n),{\dot{x}}(t_n)) \end{array}\right] . \end{aligned}$$
(8)

Typical functions \(g_i\) are constant, polynomial or trigonometric terms. A good choice of the candidate functions is essential for the validity of the thereby found equation of motion. Therefore, the functions \(g_i\) have to cover the characteristic linear and nonlinear behavior both in damping and restoring. Subsequently, the linear combination of columns of Eq. (7) which equals \(\ddot{\textbf{x}}\), can be considered as an overdetermined algebraic system of equations

$$\begin{aligned} \ddot{\textbf{x}}=\mathbf {\varTheta }(\textbf{x},\dot{\textbf{x}})\mathbf {\xi }~ \end{aligned}$$
(9)

for the unknown vector of coefficients

$$\begin{aligned} \mathbf {\xi }=\left[ \begin{array}{cccc} \xi _1,&\xi _2,&\ldots ,&\xi _m \end{array} \right] ^\top . \end{aligned}$$
(10)

In general, such a system cannot be solved exactly, especially when the data is based on real measurements. Therefore, an error-criterion has to be considered

$$\begin{aligned} \hat{\mathbf {\xi }}=\arg \min \limits _{\mathbf {\xi }\in {\mathbb {R}}^m} (\varepsilon ). \end{aligned}$$
(11)

The easiest way to predict the coefficients is minimizing the least squares error

$$\begin{aligned} \varepsilon =\Vert {\ddot{\textbf{x}}-\mathbf {\varTheta }(\textbf{x},\dot{\textbf{x}})\mathbf {\xi }}\Vert _2^2. \end{aligned}$$
(12)

Many different types of regression exist, each with certain advantages and disadvantages [36].

3.2 Least squares regression of a model type Duffing-oscillator

Based on the aim to explicitly rescale the parameters of the cubic model, Eq. (1), ordinary least squares regression is considered in the following. Rather than using a large number of nonlinear functions in the matrix \(\mathbf {\varTheta }\), only the few relevant terms from the heuristic model are considered

$$\begin{aligned} \mathbf {\varTheta }(\textbf{x},\dot{\textbf{x}})=\left[ \begin{array}{ccc} \dot{\textbf{x}},&\textbf{x},&\textbf{x}^3 \end{array}\right] . \end{aligned}$$
(13)

Besides from the states Eq. (6), also the history data of external excitation

$$\begin{aligned} \textbf{f}=\left[ \begin{array}{cccc} f(t_1),&f(t_2),&\ldots ,&f(t_n) \end{array} \right] ^\top ~ \end{aligned}$$
(14)

is known and therefore can be regarded as an additional term of the left-hand side vector

$$\begin{aligned} \underbrace{\ddot{\textbf{x}}-\textbf{f}}_{\textbf{y}}=\underbrace{\mathbf {\varTheta }(\textbf{x}, \dot{\textbf{x}})\mathbf {\xi }}_{\hat{\textbf{y}}(\mathbf {\xi })}. \end{aligned}$$
(15)

Further on \(\vec {y}\) and \(\vec {\hat{y}}(\vec {\xi })\) are called observations and predictions in accordance with the notations in context of statistical linear models. The unknown parameters are gathered in the vector

$$\begin{aligned} \mathbf {\xi }=-\left[ \begin{array}{ccc} \delta ,&\alpha ,&\beta \end{array} \right] ^\top . \end{aligned}$$
(16)

Due to the limitation of terms within the library, there is no demand for sparsity-promoting regression. Instead, the optimal parameters are defined minimizing the least squares error

$$\begin{aligned} \hat{\mathbf {\xi }}=\arg \min \limits _{\mathbf {\xi }\in {\mathbb {R}}^3} (\Vert {\textbf{y}-\hat{\textbf{y}}(\mathbf {\xi })}\Vert _2^2). \end{aligned}$$
(17)

The solution is obtained by taking the pseudoinverse \(\mathbf {\varTheta }^+\) of the library matrix

$$\begin{aligned} \hat{\mathbf {\xi }}= \underbrace{(\mathbf {\varTheta }^\top \mathbf {\varTheta })^{-1}\mathbf {\varTheta }^\top }_{\mathbf {\varTheta }^+}\textbf{y}. \end{aligned}$$
(18)

In the following, a model obtained by a regression of time series data are abbreviated by RM (regression model).

3.3 Local cubic regression models

In a first step, individual regression models have been identified associated with each experimental result. This has been done for two reasons. First of all, to elaborate the effect of solution types depending on frequency and second, to check the algorithm for robustness.

Fig. 5
figure 5

Parameters of the local RMs as function of excitation frequency (light red: data from intrawell experimental result, dark red: data from interwell or chaotic experimental result, blue line: HM) (color figure online)

Full size image

The distribution of the resulting parameters of the RMs of all experiments is shown in Fig. 5. The linear damping \(\delta \) varies in a range from 0.4 to 1.7\(\,\mathrm {s^{-1}}\) and deviates in a considerably rate from the value in HM, Eq. (3). This large deviation is due to the neglection of electromagnetic dissipation in HM and the simplified determination by means of the decay rate. For one type of solution, i.e., interwell (dark red) or intrawell (light red), respectively, and one excitation frequency the identified parameters \(\alpha , \beta \) are in general only slightly differing. Comparing different solution types, distinct deviations of the parameter values occur at least for low frequencies. As could be expected the RMs of intrawell solutions are close to the HM, Eq. (3), whereas the models of interwell solutions differ considerably, clearly recognizable from the density estimation in Fig. 5. As can be seen in [24], this is even more true for solutions with larger amplitude. It seems that the restoring force is not properly represented by a polynomial with linear and cubic terms. Furthermore, it is noticeable from Fig. 5 that the parameters of the interwell vibration at 9.25\(\,\textrm{Hz}\) are far away from the neighbors. Both statements will be discussed in more detail below.

However, before modifying the modeling a regression analysis has been elaborated exploring the model’s quality. One reliable indicator is given by the coefficient of determination

$$\begin{aligned} R^2_j(\hat{\mathbf {\xi }}_j) = 1 - \frac{\Vert \textbf{y}_j-\hat{\textbf{y}}_j(\hat{\mathbf {\xi }}_j)\Vert _2^2}{\Vert \textbf{y}_j-\bar{{\textbf{y}}}_j\Vert _2^2} , \end{aligned}$$
(19)

which is evaluated for each of the \(j=1,\ldots ,450\) experiments. Herein, \(\bar{y}\) represents the vectorized mean value of the observation. A perfect model would give 1 as the result of Eq. (19).

The results are shown in Fig. 6, plotted over excitation frequency. The color coding is similar to Fig. 5. Also, results for HM are plotted, divided in interwell, respectively, chaotic (dark blue) and intrawell (light blue) solutions.

Fig. 6
figure 6

Coefficient of determination, calculated for the the HM (blue) and RM (red). Lighter color: data from intrawell exp. result, darker color: data from interwell or chaotic exp. result (color figure online)

Full size image

Apart from a few outliers at 9.25, 9.75, 10 and \(11.75\,\textrm{Hz}\) (those at 9.25 and \(11.75\,\textrm{Hz}\) are not in the range of the plot), that will be addressed later, both models deliver satisfactory accuracy. The solutions with lower coefficient of determination between 11.75 and \(14.5\,\textrm{Hz}\) belong to chaotic solutions. Anyway the RMs yield an improvement of in average 0.034 compared to HM, i.e., constitute an improvement compared to this classical model.

In Fig. 7, trajectories of both models at excitation frequency \(8.25\,\textrm{Hz}\) are compared to corresponding experimental results. Again the closest result with respect to the distance according to Eq. (4) is shown. The figures illustrate exemplarily the general finding of a better performance of the RM (red), in case of an interwell solutions. A clear qualitative and quantitative difference can be seen in the phase portrait in Fig. 7a. Phase portraits do not reveal any information about a possible phase shift between the solutions and the experiment. For this purpose, a time series plot is shown in Fig. 7b. Therein, all signals were synchronized with the sine wave of the respective excitation to get a common time scale. A very slight phase shift of the HM can be seen in comparison to the other results. Between the RM and the experiment no visible phase shift is recognized. Further investigations of several results have shown that the phase shift is rather small in general. Moreover, it is of less importance for the energy output of an energy harvester. Therefore, only phase portraits are compared in the following.

So far, individual experimental results have been compared to the same solution types of general HM or specific RM. Figure 8a shows a case, where a simulation result from an RM with parameters determined from a chaotic solution is compared (due to an appropriate choice of initial conditions) with an experimental intrawell solution. In this special case, the RM with parameters from chaotic solution performs for intrawell solution even better than the HM!

For the interest in a model selection, different methods, like cross-validation or information criteria may be applied here [2].

However, the analysis has proven that the classical cubic modeling is not fully capable to represent the general system’s dynamics, even if a RM is used. In most cases, no intrawell solutions have been found based on interwell data, while the interwell solutions based on the intrawell model have significant deviations (similar as the HM). This can be seen in particular when comparing Figs. 7a and 8b. The interwell solution based on intrawell data shows significant larger deviations from the experimental result as the interwell solution based on interwell data.

Fig. 7
figure 7

Phase portraits a and time series b at excitation frequencies \(8.25\,\textrm{Hz}\), obtained from the experiment (black) and simulations of the HM (blue) and the RM (red). Lighter color: intrawell, darker color: interwell (color figure online)

Full size image
Fig. 8
figure 8

Selected phase portraits at excitation frequencies \(13.75\,\textrm{Hz}\) and \(8.25\,\textrm{Hz}\), obtained from the experiment (black, gray), simulations of the HM (blue) and the RM (light red). All the RM are based on intrawell data. (color figure online)

Full size image

3.4 Handling of outliers

In the previous section, several outliers, at excitation frequency \(9.25\,\textrm{Hz}\), have been mentioned, which shall be considered now more in detail. Earlier investigations in [22] have shown that in general even in cases for excitation frequencies close to the first resonance frequency, the vibration shape of the beam does not only include the first eigenshape of the beam, but also at least a small portion of the second eigenshape. In fact such outliers seem to be related to that phenomenon with a comparably significant portion of the second eigenshape. Furthermore, as Noll has shown in [24], there is also a feedback of the beam vibration on the support structure, which is an additional reason for those outliers.

A corresponding experimental phase curve is shown in Fig. 9 showing significant qualitative differences to the results considered before. As long, as just the first eigenshape is used for the discretization of the beam, it is not possible to overcome the problem of bad agreement of experimental and simulation results, even if, as in the following section, the polynomial degree of the nonlinear restoring force is extended. In fact, higher degrees of discretization have been discussed in [12, 22]. But in the actual paper, the linear regression method shall be initially applied to single degree of freedom models in comparison with experiments only.

Therefore, the authors decided not to use common methods in linear regression to overcome problems with outliers like \(L_1\)- or Huber regression [32] for a suitable robustness without prior selection of data. But since the “outlier” in Fig. 9 is mainly identified as second mode responses of the beam structure, such experimental data series are simply filtered out and omitted in case of a (more or less arbitrarily chosen, but for the actual problem well fitting) threshold value \(R^2<0.84\) while comparing the cubic RM with the experimental result as described in the previous chapter.

Therefore, in the next chapter, the following steps are performed. First, the nonlinear restoring model is extended from a cubic to a quintic one. Second, experimental outliers are excluded via the threshold value. Third, instead of identifying individual parameters for each single experimental result, a global quintic regression model shall be identified in the following for all experimental results beside the omitted outliers.

Fig. 9
figure 9

Phase portraits of an outlier experimental result

Full size image

3.5 Global quintic regression model

Taking into account the finding, that for the cubic model, simulation results deviate more or less from experiments (Fig. 6), an obvious possible refinement for the now considered global model is the extension of Eq. (1) by a quintic term with coefficient \(\gamma \) as in [12]

$$\begin{aligned} \ddot{x}(t)+\delta {\dot{x}}(t) + \alpha x(t) + \beta x^3(t) + \gamma x^5(t) = f(t). \end{aligned}$$
(20)

The idea in using this quintic regression model, abbreviated by RM\(^5\) in the following, is that it can better adjust to the nonlinear restoring characteristic. At the same time the quintic model remains simple and compact. A corresponding quintic HM (with linear, cubic and quintic term) does not exist, as the symmetric stable equilibrium positions and circular frequency allow only the determination of two parameters, Eq. (2). Instead, a HM with quintic but without cubic restoring force is considered in [12].

As described in the section before, outlier data series are neglected and the model is limited to the 1-dof response described by (20). All the remaining experimental data (427 files) are gathered in new vectors of state

$$\begin{aligned} \mathbf {\underline{x}}=\left[ \begin{array}{cccc} \textbf{x}_1^\top ,&\textbf{x}_2^\top ,&\ldots ,&\textbf{x}_{427}^\top \end{array}\right] ^\top , \end{aligned}$$
(21)

velocity

$$\begin{aligned} \dot{\mathbf {\underline{x}}}=\left[ \begin{array}{cccc} \dot{\textbf{x}}_1^\top ,&\dot{\textbf{x}}_2^\top ,&\ldots ,&\dot{\textbf{x}}_{427}^\top \end{array}\right] ^\top \end{aligned}$$
(22)

and observation

$$\begin{aligned} \mathbf {\underline{y}}=\left[ \begin{array}{cccc} \textbf{y}_1^\top ,&\textbf{y}_2^\top ,&\ldots ,&\textbf{y}_{427}^\top \end{array}\right] ^\top . \end{aligned}$$
(23)

The library is constructed with the additional quintic polynomial

$$\begin{aligned} \mathbf {\varTheta }(\mathbf {\underline{x}},\dot{\mathbf {\underline{x}}})=\left[ \begin{array}{cccc} \dot{\mathbf {\underline{x}}},&\mathbf {\underline{x}},&\mathbf {\underline{x}}^3,&\mathbf {\underline{x}}^5 \end{array}\right] , \end{aligned}$$
(24)

while the parameter vector contains the unknown parameters

$$\begin{aligned} \mathbf {\xi }=-\left[ \begin{array}{cccc} \delta ,&\alpha ,&\beta ,&\gamma \end{array} \right] ^\top . \end{aligned}$$
(25)

Similar as in Eq. (18), the pseudoinverse delivers the least squares solution

$$\begin{aligned} \begin{aligned}&\delta = 0.9\,\mathrm {s^{-1}},&\alpha =&-3558.6\,\mathrm {s^{-2}},\\ {}&\beta =82.1 \,\mathrm {mm^{-2}\,s^{-2}},&\gamma =&-1.34\times 10^{-2}\,\mathrm {mm^{-4}\,s^{-2}}. \end{aligned} \end{aligned}$$
(26)

Figure 10 compares \(R^2\) (calculated for each individual experiment) of the HM and RM\(^5\) over excitation frequency. Remarkable improvements are obtained in the middle part of the domain, where the amplitudes are large (first natural frequency of the beam). At lower and higher frequencies, the HM performed more accurate. Taking all of the data simultaneously the improvement of \(R^2\) is from 0.942 (HM) to 0.955 (RM\(^5\)).

Fig. 10
figure 10

Coefficient of determination, calculated for the the HM (blue) and RM\(^5\) (green). Lighter color: data from intrawell experimental result, darker color: data from interwell or chaotic experimental result (color figure online)

Full size image

As has been considered in [12, 24], the response diagram (Fig. 11) plotting turning points of regular solutions over excitation frequency gives a suitable indicator for a wide range validity of the models. Once again, only the experimental solutions are plotted with minimum mean distance Eq. (4). Furthermore, only results that have less than 10 different turning points, rounded to the first digit, are plotted in the graph. Thereby, all chaotic and some of the very rare high periodic solutions that have no similar counterpart in the simulation are omitted. Black represents the experiment, green the RM\(^5\) and red the HM. The RM\(^5\) shows at all regimes of higher amplitude oscillations a better consistency with the experiments.

Some phase curves are shown in Fig. 12. Figure 12a, b, d demonstrates that the global RM\(^5\) results are in general much closer to the experimental results than the global HM results are. This holds generally for both intrawell and interwell solutions. Only for small amplitude intrawell solutions in Fig. 12b, d, the HM delivers better accordance to experimental results than the RM\(^5\) does. We will look in the following section into this and try to overcome this problem by a constrained regression model, taking into account the stable equilibrium positions in the RM as it is done in the HM. The experimental interwell solution in Fig. 12b is one of the outliers which is omitted in the regression procedure as described in the previous section.

Fig. 11
figure 11

Turning points of stationary responses: experiment (black), HM (blue) and RM\(^5\) (green). Lighter color: intrawell, darker color: interwell (color figure online)

Full size image
Fig. 12
figure 12

Phase portraits at various excitation frequencies obtained from the experiment (black), HM (blue) and RM\(^5\) (green). Lighter color: intrawell, darker color: interwell (color figure online)

Full size image

Figure 13 summarizes the restoring forces

$$\begin{aligned} r(x) = \alpha x +\beta x^3~ (+\gamma x^5) \end{aligned}$$
(27)

of all the so far investigated models (the term in brackets vanishes if r belongs to the cubic RM or the HM). It can be seen from the plot that even though some of the simple cubic RM are influenced by the later on neglected outliers all results remain phenomenological plausible by means of bistability. At the same time, it is found that models based on interwell and intrawell experimental data are located at different areas within the graph. Interwell models are more spread out at lower and intrawell at higher x. Furthermore, it looks like the RM\(^5\) attempts to compensate for this inconsistency. At lower x, it is close by the static equilibrium position \(x_0\), and at higher x, it remains inside the area of interwell data. Obviously the RM\(^5\) does not exactly fit the stable equilibrium position marked by a cross in Fig. 13. To overcome this problem, in the following section, therefore a constrained RM is considered, fixing the restoring force in the equilibrium positions to vanish.

Fig. 13
figure 13

One side restoring characteristic of the symmetric models

Full size image

3.6 Constrained regression models

Constrained regression is usually performed by using Lagrange multipliers [13]. A similar but more intuitive approach is to constrain the preselected functions in advance, as it is presented in the following. The condition for the equilibrium positions \(\pm x_0\) reads

$$\begin{aligned} \alpha x_0 + \beta x^3_0 + \gamma x^5_0 = 0. \end{aligned}$$
(28)

Considering this, one of the parameters \(\alpha , \beta , \gamma \,\) within the model’s Eq. (20) can be eliminated. Eliminating \(\gamma \), a corresponding library matrix can be constructed as

$$\begin{aligned} \mathbf {\varTheta }(\mathbf {\underline{x}},\dot{\mathbf {\underline{x}}})=\left[ \begin{array}{cccc} \dot{\mathbf {\underline{x}}},&\mathbf {\underline{x}} - x_0^{-4}\,\mathbf {\underline{x}}^5,&\mathbf {\underline{x}}^3 - x_0^{-2}\,\mathbf {\underline{x}}^5 \end{array}\right] , \end{aligned}$$
(29)

while the regression parameters reduces to

$$\begin{aligned} \mathbf {\xi }=-\left[ \begin{array}{ccc} \delta ,&\alpha ,&\beta \end{array} \right] ^\top . \end{aligned}$$
(30)

Afterward, \(\gamma \,\) follows from Eq. (28). The corresponding quintic regression model with constraint is abbreviated by RM\(^{5c} \) in the following. For identification, the same overall 427 test series as in the previous section are taken into consideration. The least squares parameters of the RM\(^{5c}\) yield

$$\begin{aligned} \begin{aligned}&\delta = 0.9\,\mathrm {s^{-1}},&\alpha =&-3832.4\,\mathrm {s^{-2}},\\ {}&\beta =76.9 \,\mathrm {mm^{-2}\,s^{-2}},&\gamma =&~4.5\times 10^{-2}\,\mathrm {mm^{-4}\,s^{-2}}. \end{aligned} \end{aligned}$$
(31)

Taking all of the data considered, \(R^2\) drops down to 0.9448, but as can be seen from Fig. 14, the consistency is much more balanced between the different solution types.

Fig. 14
figure 14

Coefficient of determination, calculated for the the RM\(^5\) (green) and RM\(^{5c}\) (pink). Lighter color: data from intrawell exp. result, darker color: data from interwell or chaotic exp. result (color figure online)

Full size image

Figure 15 shows that in comparison with the RM\(^5\), the restoring force of RM\(^{5c}\) meets the equilibrium position.

Fig. 15
figure 15

Restoring characteristic of the RM\(^5\) (green) and RM\(^{5c}\) (pink)(color figure online)

Full size image

4 Conclusions

Modeling of the considered bistable magnetoelastic system is still a challenge due to the high complexity of the magnetic field forces. The actual paper applies a familiar modelling approach in a new field of application. Even though the classical heuristic model frequently applied since the very beginning of the modeling of such systems turns out to be astonishing good, all models based on regression are significantly more accurate. This statement proved to be particularly valid for high amplitude solutions. An additional high potential of the procedure lies in the adaptability through a possible great amount of nonlinear functions, if necessary also beside polynomial functions. Another additional advantage is that physical constraints as the position of the known stable equilibria (exploited in the HM) can also be included in the procedure. The results are still, as in the classical heuristic methods, equations of motion which allow for the simulation of all possible operation states, e.g., transient, stationary, free or forced vibrations. The applied method runs fast and is easy to implement. However, the main result is that cubic modeling is not well-suited to achieve accurate model fitting. Regression-based methods are appropriate tools to extend to higher-order approaches.

5 Outlook

The study offers additional starting points for further investigations and improvements of the model. For model selection, Cross-Validation or Information Criteria may be applied here [2]. To fit a model even more precisely, additional terms could easily be added to the model equations. Such models naturally may become large, but can be reduced by the so-called SINDy method (Sparse Identification of Nonlinear Dynamics) introduced in [3]. A large set of terms in the model equations are thereby concentrated to an essential quantity, e.g., via LASSO Regression. Of special interest will be, if such regression techniques like SINDy delivers similar partly physically interpretable equations, as presented here. Future work could also address the inclusion of higher modes in the model equation, corresponding to the modeling, e.g., in [12]. This may take into account that at least small portions of the second mode vibration are always present in the response even if the system is excited close to first resonance frequency [22]. Even a continuous model could possibly be generated by PDE-FIND [27] or WSINDy [19], e.g., from data acquisition via high-speed camera [22]. Otherwise, it might be necessary to ask how to handle unobserved degrees of freedom. Some related attempts are already considered in [29]. Besides the restoring characteristic the damping and hysteresis behavior related to the effect of the electromagnetic dissipation is another ongoing question [23]. In this regard, the Bouc–Wen model of hysteresis [10] might be a very effective low-dimensional expression also for multistable systems.